Skip to main content
NCBI home page
Biophysical Journal logoLink to Biophysical Journal
. 2006 Jun 2;91(6):2024–2034. doi: 10.1529/biophysj.106.083048

Structure and Dynamics of Dioxygen Bound to Cobalt and Iron Heme

Ivan Degtyarenko *, Risto M Nieminen *, Carme Rovira †
PMCID: PMC1557552  PMID: 16751243

Abstract

In this study we use ab initio molecular dynamics simulations to analyze the structure and dynamics of the oxygen ligand in models of the oxymyoglobin active site and its cobalt-substituted analog. Our calculations are performed for iron-porphyrin and cobalt-porphyrin complexes with imidazole and oxygen as axial ligands, and we investigate the effect of the distal histidine in the structure and dynamics of the metal-oxygen unit (MeO2, Me = Fe, Co). We find that the interaction between the distal histidine and the oxygen ligand is stronger for the cobalt complex than for the iron one, consistent with the superoxide ion character of the bound O2. The dynamics of the O2 ligand can be described as oscillations of the O-O axis projection on the porphyrin plane within a porphyrin quadrant combined with frequent jumps from one quadrant to another. However, the ligand motion is significantly faster for CoO2 compared to FeO2. As a result, the iron complex shows localized ligand sites, whereas for cobalt several configurations are possible. This gives support to the highly dynamic motion of the oxygen ligand found in several experiments on cobalt oxymyoglobin and model complexes and underlines the higher mobility of the CoO2 fragment compared to FeO2.

INTRODUCTION

The proteins responsible for oxygen transportation and storage in mammalian cells, hemoglobin (Hb) and myoglobin (Mb), have often been used as examples of protein conformation, dynamics, and function (1–4). It was observed early that replacement of iron by cobalt in hemoglobin (Hb) results in proteins that bind oxygen reversibly (5–7), unlike artificial hemoglobins containing other metals such as zinc, manganese, copper, and nickel. Cobalt-substituted oxymyoglobin (CoMbO2) was also characterized (7), as well as synthetic analogs (9–13). Cobalt replacement has an important advantage, which is that it is electron paramagnetic resonance (EPR) active due to the S = ½ electron configuration of Co-heme-O2, whereas the Fe-heme-O2 is EPR silent. As a result, EPR studies on cobalt-substituted oxyhemoglobin (in both α- and β-subunits) and synthetic heme models (9) helped to explain the properties of the metal-oxygen bond such as the dynamic motion of the oxygen ligand (14,15), the deformation of the porphyrin ring, and the formation of a hydrogen bond between the O2 ligand and the distal histidine residue (16–18).

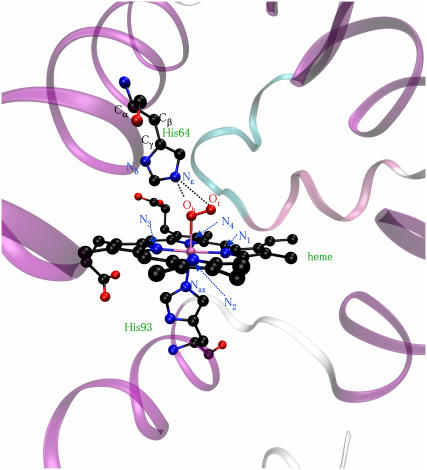
In contrast to the native iron systems, there is little structural information available for cobalt-substituted heme proteins. The only high-resolution structure available for CoMbO2 was obtained by Brucker et al. in 1996 (19). Their study proved that, indeed, the CoO2 moiety exhibits a similar end-on type of structure as the FeO2 unit in the native protein. However, small structural differences were found between the cobalt analogs and their iron counterparts. In particular, the Co-O bond (2.01 Å) is longer than the Fe-O bond (1.86 Å), and the Co-O-O angle (109° ± 5°) is significantly smaller than the Fe-O-O one (119°). There are also small differences in the position of the distal histidine (His-64). Whereas the terminal oxygen atom of the FeO2 unit (Ot in Fig. 1) lies closer to the Nɛ atom of the distal histidine than the bridging oxygen atom (Ob), the reverse is found for CoO2 (i.e., the shortest H···O distance involves Ob). These structural changes between cobalt and iron proteins suggest that there could be differences in the dynamics of the bound ligand.

FIGURE 1.

FIGURE 1

Open in a new tab

Structure of CoMbO2 (PDB entry 1YOI) and atom labeling used. Hydrogen atoms are omitted for clarity.

The dynamics of the metal-oxygen bonds have been investigated mainly for cobalt analogs (14,15,20), and the results have been typically extrapolated to iron. Common to these studies is the conclusion that the O2 ligand undergoes a fast rotational motion around the Co-O2 bond. Early EPR measurements on a nonheme cobalt-oxygen complex [O2Co(bzacen)py] concluded that the O2 ligand jumps between two bent structures (21). These results were later confirmed for CoHbO2, for which it was found that the O2 ligand rotates around the Co-O bond at a rate of ∼100 MHz (≈108 s−1) (14). This provided a different view from that obtained in x-ray structures, which give a static picture of the metal-oxygen bond. Even though there is no EPR information available on the dynamics of the FeO2 fragment in Mb and Hb, a large degree of resemblance with the cobalt analog is expected. For instance, the fourfold disorder found in the crystal structures of heme models and hemeproteins (22,23) has been interpreted as a dynamic disorder of the ligand along four equivalent sites. Nevertheless, a comparative analysis of the dynamics of the metal-ligand bonds in both cases (Fe and Co) is not yet available.

Theoretical techniques can be very useful in investigating these issues, as the calculations can be performed on cobalt and iron analogs under the same conditions. Molecular dynamics techniques have been used in a number of investigations of ligand binding to myoglobin (see for instance Czerminski and Elber (24). However, the available force fields are not able to describe either the rotational dynamics of the ligand or its electronic properties. Several first-principles studies on the structural and electronic properties of cobalt porphyrins (27,32) and oxyheme models are also available (27–33). The dynamics of the FeO2 unit were previously analyzed by one of us (33). However, to the best of our knowledge, the structure and dynamics of oxygen binding to cobalt-based heme analogs has not yet been analyzed by first-principles methods. Therefore, we report here a DFT molecular dynamics study of dioxygen bound to cobalt and iron heme. In a first step, we focus on the structure and ligand dynamics in small heme models of the type MeP(Im)O2 (Me = Fe, Co; P = porphyrin; Im = imidazole). In this case, the ligand is free to adopt any orientation. In a second step, we include the distal histidine residue in the model and analyze its effect in the structure and dynamics of the MeO2 bond.

METHODS

Structures

The initial structures of the systems investigated were taken from the optimized structures for FeP(Im)O2 models obtained previously (27). Four models of the type MeP(Im)O2 (Me = Fe, Co) and MeP(Im)O2···His (Me = Fe, Co) were constructed. The position of the distal histidine (His-64) was taken from the crystal structures of CoMbO2 (Protein Data Bank (PDB) entry 1YOI, structure at 1.65 Å resolution) (19) and FeMbO2 (PDB entry 1A6M, structure at 1 Å resolution) (34) and was modeled with an ethyl imidazole. Two different His-64 positions (hereafter named a and b) are given in the x-ray structure of FeMbO2, corresponding to a different degree of rotation of the imidazole around the Cα-Cβ bond (see Fig. 1). A separate calculation was performed for each of these conformations by constraining the Cα and Cβ atoms at their position in the crystal structure. Another calculation in which His-64 is free to adopt any orientation was also performed (in the case of the iron complex, this calculation started from position a).

Computational details

The calculations were carried out using a numerical atomic orbitals density functional theory (DFT) (35,36) approach, which has recently been developed and designed for efficient calculations in large systems and implemented in the SIESTA code (37–41). We used the generalized gradient approximation (GGA) to DFT and, in particular, the functional of Perdew, Burke, and Ernzerhof (42). The choice of this functional is based on its reliability in the description of hydrogen bonds (43) and dynamic processes in proteins (44-48). Only the valence electrons were considered in the calculation, with the core being replaced by norm-conserving scalar relativistic pseudopotentials (49) factorized in the Kleinman-Bylander form (50). (The pseudopotentials were generated using the following reference configurations: 2s22p2 for C, 3s23p3 for N, 3s23p4 for O, 1s2 for H, and 4s13d8 for Co. The cutoff radii (a.u.) were 1.25 for both the s and p components in C, 1.24 for the s and p components in N, 1.14 for the s and p components in O, 2.10 for the s and p components and 1.78 for the d component in Co, and 1.25 for the s component in H, respectively.) We used a split-valence double-ζ basis set including polarization orbitals for all atoms, as obtained with an energy shift of 50 meV (41). The integrals of the self-consistent terms of the Kohn-Sham Hamiltonian are obtained with the help of a regular real-space grid in which the electron density is projected. The grid spacing is determined by the maximum kinetic energy of the plane waves that can be represented in that grid. In the work presented here, we use a cutoff of 150 Ry, which yields a spacing between the grid points of ∼0.13 Å. We checked that the results are well converged with respect to the real space grid and the range of the atomic orbitals. The iron-containing models were computed as a singlet state (S = 0), whereas cobalt analogs were computed in the doublet (S = ½) spin state. Every calculation was running in parallel using two or four processors of an Opteron Linux Cluster. In average, one step of MD took 25 min of cumulative CPU time.

Heme complexes with doublet ground states, as well as radical states in general, are routinely studied by DFT (25–27,45–47,51). However, it is well known that the use of a monoconfigurational approach to describe doublet states is affected by an error due to the contamination of the electronic wavefunction with states of higher spin multiplicities. This error is mainly reflected on dissociation energies, but structures are less affected (52,53). In the case of CoP(Im)O2, the error is expected to be small because the computed structure and spin distribution are in agreement with experiment. Spin polarization was not used for the Fe system because it was previously demonstrated that the potential energy surface with respect to ligand orientation is not affected significantly (33). As shown in Table 1, our results obtained for the FeP(Im)O2 model reproduce fairly well those obtained previously using Car-Parrinello molecular dynamics (CPMD) (27), showing that the change from a plane wave basis set to the use of numerical atom-centered functions does not introduce any bias into the calculations. The interaction energy between the distal histidine and the oxygen ligand was computed as the difference between the energy of the MeP(Im)O2···His complex and those of the isolated fragments, MeP(Im)O2 and His, in their corresponding optimized structures. This energy was corrected by the interaction energy between the distal His and the heme, which were computed separately. The calculations of the five-coordinated complexes were done at the structure of the corresponding optimized oxyheme models. In this way the reported binding energies account only for the interaction of the ligand with the distal His.

TABLE 1.

Optimized structures for the FeP(Im)O2 complex

Model O-O Fe-Nax Fe-Nporph Fe-O <Fe-O-O Reference
CPMD/BP86 1.29 2.08 2.01–2.02 1.74 122.0 27
CPMD/PBE 1.28 2.06 2.00–2.02 1.74 122.7 This work
SIESTA/PBE 1.28 2.08 2.01–2.04 1.78 121.0 This work
Exp. (models) 1.2 2.07 1.98 1.75 131 22
Exp. (protein) 1.24 2.06 2.00–2.02 1.81 122 34
Open in a new tab

Comparison between two different approaches discussed in the text. Distances are given in angstroms, and angles in degrees.

The total energies of each system were recomputed with CPMD to avoid the basis set superposition error. Molecular dynamics simulations were performed starting from the optimized structures of the MeP(Im)O2 and MeP(Im)Inline graphicHis models (Me = Co, Fe). Each simulation was followed for at least 30 ps, using a time step of 1 fs. Only the last 28 ps were used for analysis. The same methodology used here has been recently used with success in the investigation of problems of biological relevance, including heme proteins (44–47).

RESULTS AND DISCUSSION

Equilibrium structures

MeP(Im)O2 models (Me = Fe, Co)

The main parameters defining the optimized structures of MeP(Im)O2 models (M = Fe, Co) are listed in Table 2 (see atom labeling in Fig. 1). The overall structure of the oxyheme models is close to the corresponding x-ray structures of FeMbO2 and CoMbO2. The largest discrepancy corresponds to the Co-O distance (1.94 Å), which is 4% shorter than the experimental value (2.03 Å). On the other hand, the optimum Co-O-O angle (118°) is outside the range of values given by the x-ray structure (109° ± 5°). Instead, both the Fe-O distance (1.78 Å) and the Fe-O-O angle are in good agreement with the experiment (1.81 Å and 122°, respectively). However, it should be noted that the Co-O-O angle in CoMbO2 is given with a large error bar (±5°). On the other hand, EPR measurements in CoMbO2 predict a larger angle (120°) (54), which is much closer to our results. Therefore, our results are within the range of values reported in experimental studies. It will be also seen later on that the values of the Co-O distance and the Co-O-O angle increase when the room temperature dynamics of the ligand is taken into account.

TABLE 2.

Optimized structures of the models investigated

Model Me-O <Me-O-O O-O Me-Nax Me-Nporph φ*
FeP(Im)O2 1.78 121.0 1.28 2.08 2.01–2.04 45.5
FeP(Im)O2···His 1.77 (a) 118.8 (a) 1.30 (a) 2.12 (a) 2.01–2.04 (a) 40.7
1.77 (b) 118.9 (b) 1.30 (b) 2.11 (b) 2.01–2.04 (b) 38.8
FeP(Im)O2···His free† 1.77 119.8 1.30 2.11 2.01–2.04 40.7
Exp (FeMbO2)‡ 1.81 122 1.24 2.06 2.00–2.02 21.5
CoP(Im)O2 1.94 117.7 1.28 2.08 2.01 49.6
CoP(Im)O2···His 1.89 116.4 1.30 2.08 2.00–2.02 36.1
CoP(Im)O2···His free 1.91 116.9 1.30 2.07 2.00–2.01 45.3
Exp (CoMbO2)§ 2.03 109 ± 5 1.18 2.08 1.98–2.09 −2.1
Open in a new tab

Heme structure (Me = Fe, Co). Distances are given in angstrom and angles in degrees.

*

N1-Me-Ob-Ot dihedral angle (Me = Fe, Co).

†

The distal histidine is free to adopt any position.

‡

From Reference 34.

§

From Reference 19.

The main differences between iron and cobalt complexes concern the local structure of the MeO2 fragment. The iron complex shows a shorter bond distance and a larger angle (Fe-O = 1.78 Å, Fe-O-O angle = 121°) than the cobalt analog (Co-O = 1.94 Å, Co-O-O angle = 118°). Thus, there is a 0.6 Å increase in the metal-oxygen bond and a 3° decrease in the metal-oxygen angle on changing iron for cobalt. The same trends are observed experimentally, although the differences are larger (0.22 Å and 13°, respectively) due to the above-mentioned discrepancies between the computed and experimental structures of the Co-O2 fragment.

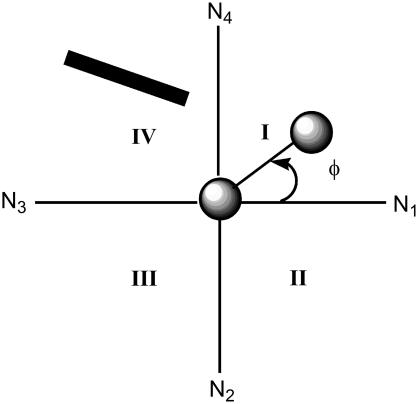
The orientation of the O2 molecule with respect to the porphyrin plane was characterized using the N1-Me-Ob-Ot dihedral angle (φ in Fig. 2). This angle is ≈45° when the O2 molecular axis bisects a porphyrin quadrant and ≈0° when it overlaps an Fe-Nporph bond. Both cobalt and iron models exhibit a bisecting orientation (φ = 46–50° for CoP(Im)O2 and 45° for FeP(Im)O2, according to Table 2), similar to that which has been observed for heme models such as the picket-fence porphyrin (22,29,55) as well as iron-heme models (27–31). The bisecting orientation is favored from steric and electronic points of view. On one hand, it avoids the steric repulsion between the ligand axis and the Me-Nporph bonds. On the other, it maximizes the interaction between the pπ orbitals of O2 and the dπ orbitals of the metal, which are oriented along the bisectors (22). The values of φ in the protein do not follow this trend because the O2 ligand shows an intermediate orientation between overlapping and bisecting for FeMbO2 (φ = 21°) and purely overlapping for CoMbO2 (φ = −2° in Table 2). This suggests that the interaction with the nearby protein residues (the distal histidine) could influence the ligand orientation.

FIGURE 2.

FIGURE 2

Open in a new tab

Porphyrin quadrant definition. The projection of the imidazole plane of His-64 on the porphyrin plane is represented with a bold line. The projection of the oxygen molecule on the porphyrin plane is shown in ball and stick.

Effect of the distal histidine

Tables 2 and 3 list the main parameters defining the optimized structures of the FeP(Im)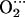Inline graphicHis and CoP(Im)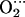Inline graphicHis models. As shown in Table 2, the presence of the distal histidine quantitatively changes the structure of the MeO2 fragments. The O-O distance increases (0.02 Å), the Me-O-O angle decreases (≈1° for Co and ≈2° for Fe), and the Me-O distance also decreases (0.01 Å for Fe and 0.04 Å for Co) when His-64 is present. The lengthening of O-O and shrinking of Me-O are an indication of hydrogen bond formation and can be rationalized in terms of variations in the Me–O2 back bonding (i.e., the interaction of the d-Fe levels with the partially occupied π* orbitals of O2). When a positive charge approaches the ligand (such as the proton of His-64), π* orbitals are energetically stabilized. As they get closer in energy to the Fe-d orbitals, the back-bonding increases. The shift in the electron population of the orbitals (from the d-Fe orbitals to the π* orbitals of O2) decreases the Me-O bond distance while increasing the O-O distance. Similar arguments have been used to rationalize the variations on the Fe-CO structure and vibrations of carbonmonoxymyoglobin (56). The decrease of the Me-O distance is more noticeable for Co because of the longer Co-O bond and the fact that the Ob atom is closer to the Nɛ-H of His-64 than in the case of the iron complex. In contrast, the terminal oxygen atom (Ot) is closer to His-64 for FeP(Im)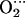Inline graphicHis than for CoP(Im)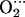Inline graphicHis. As a consequence, the effect of the distal histidine on the angle is more pronounced for Fe than for Co. In the case of iron, we also observe a lengthening of the distance with the proximal histidine due to the presence of the distal histidine. These trends are independent of the two positions of the distal His given in the crystal structure (a and b) and whether the distal His is free to move or not (Table 2).

TABLE 3.

Optimized structures of the M-P(Im)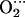Inline graphicHis complexes (Me = Fe, Co): hydrogen-bond parameters

Model < Nɛ-H···Ot < Nɛ-H···Ob Nɛ-H Ob···Nɛ Ot···Nɛ Ob···HNɛ Ot···HNɛ
FeP(Im)O2···His 160.2 135.1 1.04 (a) 3.03 (a) 2.72 (a) 2.27 (a) 1.72 (a)
171.1 138.1 1.04 (b) 3.12 (b) 2.79 (b) 2.17 (b) 1.76 (b)
FeP(Im)O2···His free 160.2 135.1 1.04 3.32 2.87 2.50 1.87
Exp (FeMbO2)† 142.5* 113.6* – 3.02 (a) 2.67 (a) – –
160.1* 136.8* 3.08 (b) 2.97 (b) – –
CoP(Im)O2···His 169.6 135.1 1.04 3.10 2.79 2.27 1.76
CoP(Im)O2···His free 170.2 139.5 1.04 3.30 2.87 2.44 1.85
Exp (CoMbO2)‡ 171.7* 139.9* – 2.72 3.01 – –
Open in a new tab

Distances are given in angstroms, and angles in degrees.

*

Value obtained on adding a hydrogen atom to the Nɛ of His-64.

†

From Reference 34.

‡

From Reference 19.

Another effect of the distal histidine is a small change in orientation of the O2 ligand, as reflected by the decrease of φ (by ≈5° for the iron complex and ≈12° for the cobalt analog). These variations, which increase the agreement with the x-ray structure, are due to the formation of a hydrogen bond interaction between O2 and His-64. The bisecting conformation (φ = 45°), which is the optimum one for MeP(Im)O2, would lead to too short a Nɛ-H…Ot distance in MeP(Im)O2···His. Therefore, the ligand changes orientation to optimize the hydrogen bond interaction with His-64. This effect is less pronounced when His is free because it is further away from the ligand. Therefore, the distal His affects the rotational orientation of the oxygen ligand, bringing it closer to the overlapping conformation. Nevertheless, the final value of φ is still far from the one given by experiments, suggesting that other factors such as temperature effects could affect the ligand orientation. The room temperature dynamics of the ligand are discussed in the next section.

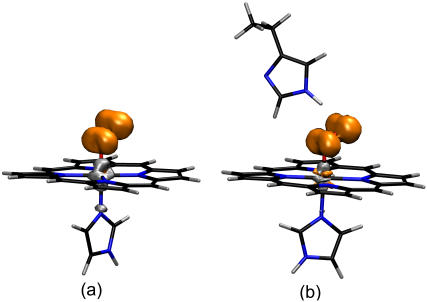
It is also interesting to determine the localization of the unpaired electron of oxycobalt myoglobin and the effect of the distal histidine in its distribution. Several studies have demonstrated that the unpaired electron that gives rise to the EPR absorption of oxy cobaltous proteins and compounds resides primarily on the bound oxygen (5,11,21,54,57). Therefore, we analyzed the spin density distributions obtained for CoP(Im)O2 and CoP(Im)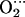Inline graphicHis. Our results show that the spin density is mainly concentrated on the O2 molecule (Fig. 3), with a small contribution of the cobalt. The relative weights are 8% (Co) and 92% (O2) in the CoP(Im)O2 model (Fig. 3 a). The presence of the distal His (Fig. 3 b) slightly increases the relative contribution of O2, which accounts for 95% of the total spin density. Therefore, our results are in good agreement with experiments and show that the shape of the spin density distribution of oxycobalt myoglobin is an intrinsic property of the active center.

FIGURE 3.

FIGURE 3

Open in a new tab

Spin density distribution in (a) CoP(Im)O2 and (b) CoP(Im)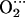Inline graphicHis.

Ligand dynamics

MeP(Im)O2 models (Me = Fe, Co)

A molecular dynamics simulation of MeP(Im)O2 (M = Fe, Co) was performed for a total time of 30 ps, with an average temperature of 300 K. To define the ligand orientation with respect to the porphyrin plane, we used the N1–Me–Ob–Ot torsional angle (φ), defined in Fig. 2. Detailed information on the dynamics of the oxygen ligand in FeP(Im)O2 is given in Rovira et al. (33). Although the simulation time sampled here is much larger (30 ps vs. 15.5 ps (32)), the main features of the dynamics remain unchanged. Therefore, here we just briefly discuss the most salient aspects of the ligand dynamics, as they will be used as a reference to analyze other models.

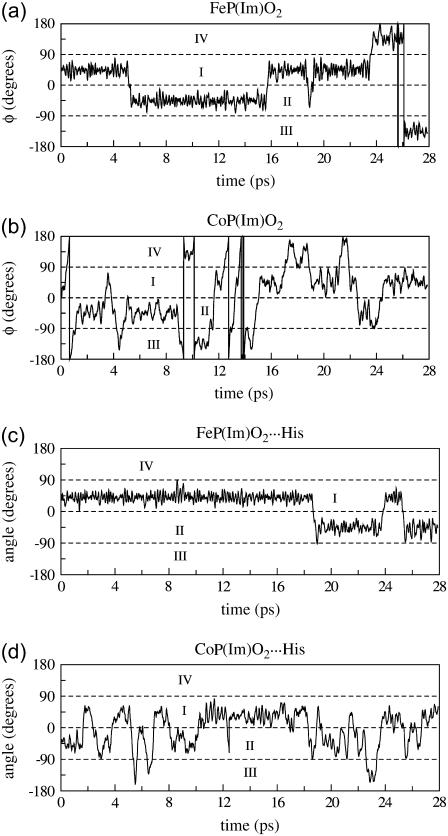
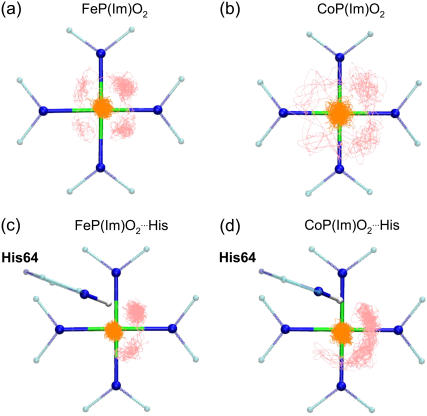
The time evolution of φ is shown in Fig. 4 a. During the first period of the simulation, the O–O axis projection on the porphyrin plane lies on the first quadrant (I), oscillating around the equilibrium conformation (φ = 45°). After ≈5 ps, the ligand jumps over the Fe–N2 bond toward the second quadrant. Another transition takes place at ≈16 ps (back to I), and eventually all quadrants are sampled. The transitions among quadrants take place via rotation of the O2 molecule around the Fe–O axis and involve conformations with a more open Fe-O-O angle (124°) and a slightly tilted Fe-O bond (3–5°) with respect to the z axis, as previously reported (33). These results provide direct evidence for the fast rotational motion of O2 around the Fe-O bond, explaining the fourfold disorder found in the crystal structure of synthetic heme models (22). They also confirm that the O-O/Fe-N overlapping configuration is the transition state for the dynamic motion of O2 between the porphyrin quadrants (58–60).

FIGURE 4.

FIGURE 4

Open in a new tab

Rotation of the O2 ligand around the Me-O bond: (a) FeP(Im)O2, (b) CoP(Im)O2, (c) FeP(Im)O2···His, and (d) CoP(Im)O2···His.

As a result of the rotational motion of the ligand, the O-O axis projection on the porphyrin plane visits all porphyrin quadrants, as shown by an analysis of the residence time of the O-O axis projection on each porphyrin quadrant (Table 4). This is also reflected in the distribution of the projection of the Ob and Ot positions on the porphyrin plane, shown in Fig. 5 a. The most sampled orientations correspond to regions near the bisecting conformations (φ = ±45°, ±135°). The nonsymmetry of the distribution is due to the limited time sampled in the simulation. It is expected that, for longer times, the axial ligands would sample all porphyrin quadrants with equal probability.

TABLE 4.

Ligand residence times on each porphyrin quadrant (I–IV), defined as the percentage of the total time in which the projection of the Ot position on the porphyrin plane lies on a given quadrant

Quadrant FeP(Im)O2 CoP(Im)O2 FeP(Im)O2···His CoP(Im)O2···His
I 25 35 78 54
II 13 13 22 40
III 19 15 0 6
IV 43 37 0 0
Open in a new tab
FIGURE 5.

FIGURE 5

Open in a new tab

Distribution of the projection of the Ob and Ot atoms on the porphyrin plane. (a) FeP(Im)O2, (b) CoP(Im)O2, (c) FeP(Im)O2···His, and (d) CoP(Im)O2···His. Only the central part of the porphyrin ring (Fe, N, and Cα atoms) is shown.

The motion of the oxygen ligand in CoP(Im)O2 is shown in Fig. 4 b. Similarly to the iron complex, the O2 ligand undergoes sizable oscillations of the φ angle within one porphyrin quadrant, with frequent jumps over the Fe-Nporph bonds. However, the frequency of these jumps is higher than in the case of the iron complex. A way to quantify the rotational dynamics of the ligand is by counting the number of times per picosecond that the O-O axis projection moves across over one Fe-Np bond (either clockwise or counterclockwise). This defined a hopping frequency (νhop). The values νhop obtained from the simulations are listed in Table 5. The hopping frequency for FeO2 turns out to be six times smaller than that of CoO2. In other words, the rotation of the oxygen around the metal-oxygen bond is six times faster for the cobalt analog than for its native counterpart. This suggests that the energy barrier for ligand rotation around the metal-oxygen bond is smaller for the cobalt models. As a way to determine this barrier, we computed the energy difference between the overlapping and bisecting conformations by fixing the orientation of the O2 and optimizing the remaining degrees of freedom. In the case of FeP(Im)O2, we obtained an energy barrier of 1.3 kcal/mol, whereas the same calculation for CoP(Im)O2 gives a value lower than 0.5 kcal/mol (i.e., the rotation becomes practically barrierless). In both cases, the energy is insensitive to the imidazole orientation and small porphyrin distortions. The fact that the Co-O bond is longer than Fe-O is probably the cause of these differences (i.e., there is less steric hindrance between the O-O bond and the Co-Nporph bonds). Because this is a common feature of the heme complexes investigated here, we suggest that the oxygen ligand in cobalt heme analogs will always be more flexible than their iron counterparts.

TABLE 5.

Number of times that the O-O axis projection on the porphyrin plane crosses a Fe-Nporph bond ñ and the hopping frequency νhop

Structure ñ νhop (ps−1)
FeP(Im)O2 7 0.25
CoP(Im)O2 40 1.43
FeP(Im)O2···His 7 0.25
CoP(Im)O2···His 50 1.79
Open in a new tab

ñ = n+ + n− (n+ = clockwise jump, n− = counterclockwise jump).

ν = (n+ + n−) / tsim, where tsim is the simulation time.

Comparison of our results (hopping frequencies) with the experimental data (rate of rotation) is not straightforward because only those hops leading to a complete rotation around Me-O contribute to the measured rotational rate. In the case of CoP(Im)O2, we observed three complete rotations of the ligand during the total simulation time (28 ps), whereas for FeP(Im)O2 we only observed one. This gives rates of rotation of 10−1 cycles/ps (Co) and 4 × 10−2 (Fe), again reflecting the faster motion of Co with respect to Fe. These values should be considered as approximate, as our simulation is not long enough to give a reliable value for the rate of rotation. Nevertheless, the higher value we obtain compared to experiment (10−4 cycles/ps in CoHbO2) (14) is probably due to the absence of hydrogen bond interaction between the ligand and the distal His, which is expected to slow down the rotational motion of the ligand. Therefore, our results predict that for a noninteracting MeO2 unit, the ligand will be rotating at a rate of ≈10−1 cycles/ps (Co model) and ≈10−2 cycles/ps (Fe model).

Effect of the distal His

When the distal His is included in the model, the spatial symmetry with respect to the four porphyrin quadrants is broken. Therefore, independently of the length of the simulation, the ligand should not sample all porphyrin quadrants with the same probability. For instance, the interaction with His-64 is maximal when the O-O projection lies on quadrant I because the Nɛ-H bond points in the direction of the electron density around each oxygen atom. Small rotations of His-64 around the Cα-Cβ and Cβ-Cγ bonds can accommodate the ligand along quadrants I and II, whereas sampling quadrant III requires a larger motion of His-64. On the other hand, the probability of sampling quadrant IV is expected to be relatively low because the distance between the Nɛ-H of His-64 and the O2 ligand would become too short, leading to a repulsive interaction, unless the His-64 moves so as to increase the Nɛ-H…O2 distance (e.g., by rotating around Cα-Cβ and/or Cβ-Cγ, defined in Fig. 1). Therefore, it is expected that the residence time of the ligand in each porphyrin quadrant would decrease in the order I > II > III ≫ IV. This is very similar to what we obtain in the simulation. As shown in Table 4 (fourth column) and Fig. 5 c, only quadrants I and II are sampled for FeP(Im)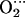Inline graphicHis, with residence times 78 (I) and 22 (II). The cobalt complex samples more configurations than the iron complex (Fig. 5, c and d), and their relative residence times, 54 (I), 40 (II), 6 (III), and 0 (IV), show the expected trend given the arguments discussed above. Interestingly, the imidazole of His-64 rotates (mainly around Cβ-Cα) so as to accommodate the ligand in its motion. Similar types of rotations in the picosecond time scale have been observed in classical MD simulations of carbonmonoxymyoglobin (61). Another difference between iron and cobalt complexes is the occurrence of configurations near the overlapping conformation (φ = 0 in Fig. 2). As was found for the small models lacking His-64 (Fig. 5, a and b), the overlapping conformations are more populated for Co than for Fe. This is also reflected in the oscillations of the φ angle, which are larger for Co than for Fe (Fig. 4, c and d), as well as in the larger values of νhop obtained for Co compared to Fe (Table 5). Therefore, we again find that the rotation of O2 around the Me-O2 bond is much faster for Co than for Fe. In addition, whereas in the iron complex the ligand shows a clear preference for the bisecting conformation, in the cobalt complex it is essentially free to adopt any orientation. The limited-time samples in our simulations (28 ps) preclude computing the rate of ligand rotation because we did not observe any complete rotation of the ligand. On the other hand, this is consistent with the experimental evidence that one full rotation occurs every ≈104 ps (15).

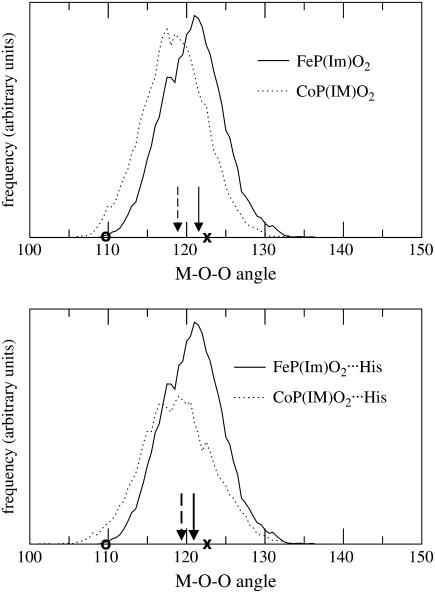
As mentioned in the Introduction, the Co-O-O angle reported in the x-ray analysis of CoMbO2 (109 ± 5°) (19) is much smaller that the one reported for FeMbO2 (122°) (34). This is in contrast to the results from structure optimization, which give a Co-O-O angle only 2–3° smaller than the Fe-O-O angle (Table 2). In addition, the computed Co-O distance is quite different from (0.1 Å shorter than) the experimental one. Given this situation, we decided to investigate whether the high flexibility of the CoO2 unit could be the reason for this discrepancy. Interestingly, the average value of the Co-O distance obtained from the simulation is 0.05 Å longer than the equilibrium distance, whereas for the iron complexes both values coincide. A similar situation occurs with the Me-O-O angles (Fig. 6). In the case of iron, the average angle is in good agreement with the x-ray structure (122°). The angle distribution is somewhat wider for Co, especially in the complexes including the distal histidine. The average angle (shown in arrows) shifts to a smaller value (119°) but is still far from the experimental data (109 ± 5°). This discrepancy could be due to the limitations of the computational approach used. It could also arise from the underestimation of the angle in the crystal structure of CoMbO2 due to 1), its lower resolution with respect to the structure of FeMbO2, and 2), the high flexibility of the CoO2 unit, which precludes assigning a static orientation (a fixed value of φ) to the ligand. The assignment becomes easier for the iron models because the ligand is less flexible. In fact, the average value of φ obtained from the FeP(Im)O2···His simulation is 20.6°, which is in good agreement with the experimental value (21°, according to Table 2).

FIGURE 6.

FIGURE 6

Open in a new tab

Distribution of the Me-O-O angle obtained from the molecular dynamics simulation (Me = Fe, Co). The arrows point toward the average angle obtained from the simulation. The x-ray values for the Me-O-O angle are marked by a cross (Me = Fe) or an empty circle (Me = Co).

His···O2 interaction

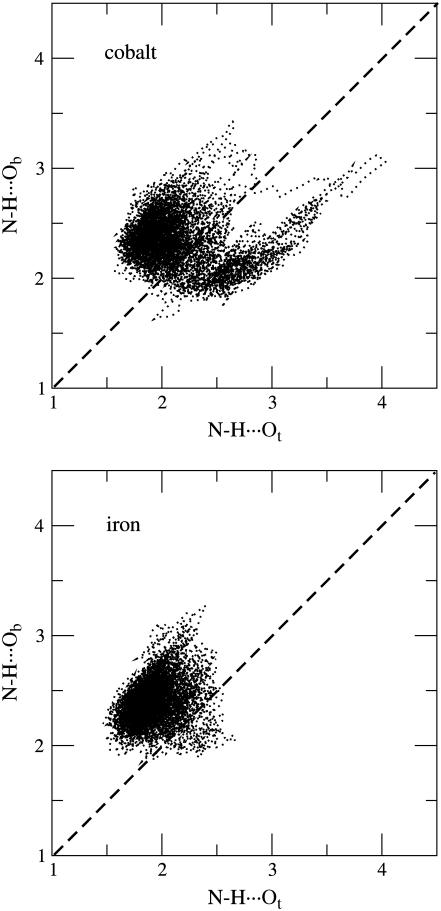
The structural parameters defining the interaction between the ligand and the distal histidine in the optimized structures are listed in Table 3. In the case of iron, Ot is the oxygen atom that is closest to His, as is found in experiments. In the case of Co, the closest oxygen atom is also Ot (Ot···H < Ob···H). However, the x-ray structure shows the reverse situation (Ot···H > Ob···H). To further investigate this aspect, we analyzed the distance between both Ot and Ob atoms and the NɛH hydrogen atom during the MD simulation. Fig. 7 shows a two-dimensional representation of the Nɛ-H···Ob and Nɛ-H···Ot values. The region above the diagonal corresponds to the situation in which Nɛ-H···Ot < Nɛ-H···Ob (i.e., the shortest distance involves Ot), and the region below the diagonal corresponds to the reverse. It is apparent that for the iron complex most of the values fall above the diagonal, i.e., the Nɛ-H···Ot < Nɛ-H···Ob. In contrast, in the case of the cobalt complex, there is a sizable number of configurations for which the Nɛ-H···Ob distance is shorter than the Nɛ-H···Ot one (i.e., values below the diagonal). Therefore, even though the Nɛ-H···Ot interaction is shorter than the Nɛ-H···Ob one in the optimized structure of CoP(Im)O2···His, there is a significant probability of finding the reverse at room temperature. If we restrict our analysis to configurations in which a putative Nɛ-H…O hydrogen bond is expected to be geometrically favored (H···O 2.5 Å and 140° < Nɛ-H-O < 160°) (43), we find that for the iron complex the shortest interaction always involves Ot, whereas for the cobalt analog this occurs 75% of the time. Therefore, although for the Fe complex Ot is always closer to His than Ob, both scenarios (H···Ot < H···Ob and H···Ot > H···Ob) are possible for the cobalt complex. This is in agreement with the x-ray structure of oxycobalt myoglobin, in which Ob is closer to His than Ot. Even though this is not the most sampled configuration observed in the simulation, it has a significant probability of being present, something that that does not occur for the iron complex. On the other hand, the fact that the analysis of the equilibrium structures leads to different conclusions illustrates the need to take into account dynamic effects to interpret the experimental data for highly flexible units such as the CoO2 fragment.

FIGURE 7.

FIGURE 7

Open in a new tab

Two-dimensional distribution of the Nɛ-H···Ot and Nɛ-H···Ob bonds in (a) FeP(Im)O2···His and (b) CoP(Im)O2···His.

It is interesting to relate the above distance analysis with the occurrence of a hydrogen bond interaction between His and O2. Several studies in both iron and cobalt myoglobin and hemoglobin have demonstrated that there is a hydrogen bond between the terminal oxygen and the Nɛ-bound proton on the imidazole of the distal histidine (14,17,62,63). Even though this interaction is believed to be an important factor in controlling oxygen affinity (64), the strength of the hydrogen bond for both metal complexes remains controversial. Although photolysis experiments suggest that there is a stronger hydrogen bond to the distal histidine in FeMbO2 versus CoMbO2 (65), the reverse is predicted by calculations on the cobalt picket fence porphyrin using a parameterized interaction potential (66). In addition, it is not known whether the hydrogen bond interaction involves both oxygen atoms or only one of them. Therefore, it is interesting to compare the properties of the hydrogen bond interaction in both iron and cobalt complexes.

Our calculations give a value of 3.7 kcal/mol for hydrogen bond interaction between the oxygen ligand and the distal His in FeP(Im)O2···His. This value is similar to those reported in previous DFT investigations (28,31,56). The hydrogen bond energy of the cobalt analog has not yet been quantified from a theoretical point of view. Nevertheless, given the superoxide anion-like character of the oxygen ligand (i.e., 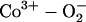Inline graphic, as reflected in the fact that the spin density distribution is mainly localized on the oxygen molecule), it is expected that CoO2 forms a stronger bond with His-64. In fact, we obtained a value of 4.7 kcal/mol for the hydrogen bond interaction in CoP(Im)O2···His. An obvious question at this point is why does the ligand rotate around the Me-O bond given the relatively strong His···O2 interaction in the equilibrium structure? The answer to this question can be related to the difference in mobility of the two oxygen atoms in the dynamics and its role in the hydrogen bond interaction. As shown in Fig. 5, the terminal oxygen atom moves around the porphyrin quadrants, eventually losing the interaction with His. Instead, the bridging oxygen is confined in a small region around the equilibrium position, thus keeping the interaction with His during the whole trajectory. This indicates that the bridging oxygen is responsible for keeping the hydrogen bond interaction during the rotational motion of the ligand and that the position of Ot is less relevant.

In summary, our calculations give support to previous studies on the existence of a hydrogen bond interaction between the bound ligand and the distal histidine (14,17,62,63). We show that this interaction is due to the bridging oxygen atom and predict that it is somehow weaker for the native iron system than for the cobalt analog. In addition, the rotational motion of the oxygen around the Me-O bond is faster for Co than for Fe. Therefore, our calculations show that both the affinity and dynamics of ligands in cobalt-based heme proteins are different from those of the iron-based compounds. This difference may have implications in practical work on artificial enzymes or gas sensors.

SUMMARY AND CONCLUSIONS

Cobalt is commonly used as an analog for iron in structural and spectroscopic studies of oxygen binding and oxygen activation of hemoglobin and myoglobin. In this work we have investigated the structure and dynamics of the MeO2 fragments (Me = Fe, Co) in oxymyoglobin (MbO2) and cobalt-substituted oxymyoglobin (CoMbO2) to quantify differences between the two proteins that could explain the differences found in their high-resolution crystal structures. Our calculations are performed in MeP(Im)O2 models (Me = Fe, Co; Im = imidazole; P = porphyrin), and the effect of the distal histidine in the structure and dynamics of the MeO2 unit is analyzed.

Two types of calculations are performed: static calculations (structure optimizations) and molecular dynamics simulations based on DFT. Our optimized structures are in good agreement with experiments for most structural parameters except for those defining the CoO2 unit, suggesting that the position of the oxygen ligand might be largely influenced by thermal motion. The spin density distribution of the cobalt complexes reflects that, in agreement with EPR experiments, most of the spin density is localized on the oxygen molecule, and the shape of the distribution is not significantly influenced by the presence of the distal histidine.

Molecular dynamics simulations at room temperature show that in both cases (iron and cobalt models) the oxygen ligand undergoes a fast rotational motion around the metal-oxygen bond. The dynamics of the ligand can be described as oscillations of the oxygen axis projection on the porphyrin plane within a given porphyrin quadrant, combined with jumps from one quadrant to another. This mechanism is fully consistent with the interpretation of previous structural and spectroscopic studies of heme analogs and provides a dynamic picture of these highly flexible metal-oxygen bonds. Even though both cobalt and iron models follow this general picture, the dynamics of the FeO2 and CoO2 units exhibit quantitative differences. First of all, the rotational motion of the oxygen around the Me-O bond is faster for Co than for Fe. For instance, in the iron complex it takes several picoseconds (6–7 ps on average) to undergo a transition from one porphyrin quadrant to another, but this time is reduced to 1–2 ps for the cobalt complex. This is due to the low energy barrier associated with the ligand rotation around the Co-O bond (≈0.5 kcal/mol). As a consequence, the oscillations of the ligand within a porphyrin quadrant are much larger for Co than for Fe, and the overlapping conformation becomes almost as populated as the bisecting conformation. Because of the high flexibility of the O2 ligand, it is not possible to assign a unique structure to the CoO2 unit. This is probably the reason why the orientation of the O2 ligand in the optimized structure (φ = 45°) is very different from the value given in the high-resolution x-ray structure of CoMbO2 (φ = 2°), as none of these approaches captures the dynamics of the bound ligand. In the case of FeO2, the bisecting conformation is clearly favored with respect to the overlapping conformation, and, therefore, static calculations and x-ray measurements lead to similar conclusions. Another difference between iron and cobalt complexes concerns the type of interaction with the distal histidine residue. Our calculations are consistent with the existence of a hydrogen bond in both FeMbO2 and CoMbO2, giving support to previous studies. However, the interaction is stronger for cobalt than for iron (4.7 kcal/mol and 3.7 kcal/mol, respectively). On the other hand, for the Fe complex the terminal oxygen atom (Ot) is always closer to the histidine NɛH hydrogen than the bridging one (Ob), whereas for the cobalt complex both scenarios (H···Ot < H···Ob and H···Ot > H···Ob) are possible, consistent with the x-ray structure. Finally, it is worth pointing out that the equilibrium structures do not reflect this trend, as they predict that the terminal oxygen atom is closer to His in both cases. Hence, caution needs to be taken in interpreting the results from static calculations for these highly flexible metal-ligand bonds.

Acknowledgments

The authors thank Dr. Dave Wood for the careful reading the manuscript and Profs. Enric Canadell and Pablo Ordejón for stimulating discussions.

This work was supported by the Generalitat de Catalunya (grant 2005SGR-00036), the Ministerio de Educación y Ciencia (grant FIS2005-00655), and the Academy of Finland (Center of Excellence Grant 2000–2005). The computer resources were provided by the Barcelona Supercomputing Center (BSC) and Helsinki University of Technology (M-grid project). C.R. acknowledges a Ramón y Cajal contract from the MEC. I.D. acknowledges the HPC mobility program of the European Union for three collaborative visits to Barcelona.

References

  • 1.Berg, J. M., J. L. Tymoczko, and L. Stryer. 2002. Biochemistry, 5th ed., W. H. Freeman, New York.
  • 2.Perutz, M. F. 1990. Myoglobin and haemoglobin: role of distal residues in reactions with haem ligands. Trends Biochem. Sci. 14:42–44. [DOI] [PubMed] [Google Scholar]
  • 3.Sage, J. T., and P. M. Champion. 1996. Small substrate recognition in heme proteins. Compr. Supramol. Chem. 5:171–213. [Google Scholar]
  • 4.Parak, F. G., and G. U. Nienhaus. 2002. Myoglobin, a paradigm in the study of protein dynamics. Chem Phys Chem. 3:249–254. [DOI] [PubMed] [Google Scholar]
  • 5.Hoffman, B. M., and D. H. Petering. 1970. Coboglobins. Oxygen-carrying cobalt-reconstituted hemoglobin and myoglobin. Proc. Natl. Acad. Sci. USA. 67:627–643. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6.Spilburg, C. A., B. M. Hoffman, and D. H. Petering. 1972. Coboglobins. Influence of the apoprotein on oxygen binding to cobaltomyoglobin. J. Biol. Chem. 247:4219–4223. [PubMed] [Google Scholar]
  • 7.Hoard, J. L., and W. R. Scheidt. 1973. Stereochemical trigger for initiating cooperative interaction of subunits during oxygenation of cobaltohemoglobin. Proc. Natl. Acad. Sci. USA. 70:3919–3922. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8.Reference deleted in proof.
  • 9.Collman, J. P., J. I. Braumann, K. M. Doxsee, T. R. Halbert, S. E. Hayes, and K. S. Suslick. 1978. Oxygen binding to cobalt porphyrins. J. Am. Chem. Soc. 100:2761–2766. [Google Scholar]
  • 10.Collman, J. P., and L. Fu. 1999. Synthetic models for hemoglobin and myoglobin. Acc. Chem. Res. 32:455:463. [Google Scholar]
  • 11.Collman, J. P., Y.-L. Yan, T. Eberspacher, X. Xie, and E. I. Solomon. 2005. Oxygen binding of water-soluble cobalt porphyrins in aqueous solution. Inorg. Chem. 44:9628–9630. [DOI] [PubMed] [Google Scholar]
  • 12.Steiger, B., J. S. Baskin, F. Anson, and A. H. Zewail. 2000. Femtosecond dynamics of dioxygen-picketfence cobalt porphyrins: ultrafast release of O2 and the nature of the dative bonding. Angew. Chem. Int. Ed. 39:257–260. [PubMed] [Google Scholar]
  • 13.Scheidt, W. R., and J. L. Hoard. 1973. Stereochemistry of low-spin cobalt porphyrins.1. Structure and bonding in a nitrosylcobalt porphyrin and their bearing on one rational model for oxygenated protoheme. J. Am. Chem. Soc. 95:8281–8288. [DOI] [PubMed] [Google Scholar]
  • 14.Walker, F. A., and J. Bowen. 1985. EPR evidence for hydrogen bond donation to the terminal oxygen of Co-O2 model compounds and cobalt oxymyoglobin. J. Am. Chem. Soc. 107:7632–7635. [Google Scholar]
  • 15.Bowen, J. H., N. V. Shokhirev, A. M. Raitsimring, D. H. Buttlaire, and F. A. Walker. 1997. EPR studies of the dynamics of rotation of dioxygen in model cobalt(II) hemes and cobalt-containing hybrid hemoglobins. J. Phys. Chem. B. 101:8683–8691. [Google Scholar]
  • 16.Ikeda-Saito, M., R. S. Lutz, D. A. Shelley, E. J. McKelvey, R. Mattera, and H. Hori. 1991. EPR characterization of the stereochemistry of the distal heme pocket of the engineered human myoglobin mutants. J. Biol. Chem. 266:23641–23647. [PubMed] [Google Scholar]
  • 17.Kitagawa, T., M. R. Ondrias, D. L. Rousseau, M. Ikeda-Saito, and T. Yonetani. 1982. Evidence for hydrogen bonding of bound dioxygen to the distal histidine of oxycobalt myoglobin and haemoglobin. Nature. 298:869–871. [DOI] [PubMed] [Google Scholar]
  • 18.Yonetani, T., H. Yamamoto, and T. Iizuka. 1974. Studies on cobalt myoglobins and hemoglobins. J. Biol. Chem. 248:2168–2174. [PubMed] [Google Scholar]
  • 19.Brucker, E. A., J. S. Olson, G. N. Phillips, Y. Dou, and M. Ikeda-Saito. 1996. High resolution crystal structures of the deoxy, oxy, and aquomet forms of cobalt myoglobin. J. Biol. Chem. 271:25419–25422. [DOI] [PubMed] [Google Scholar]
  • 20.Herta, C., H. Winkler, R. Benda, M. Haas, and A. X. Trautwein. 2002. Dynamic structural disorder of the FeO2 moiety in oxymyoglobin studied by nuclear resonant forward scattering of synchrotron radiation. Eur. Biophys. J. 31:478–484. [DOI] [PubMed] [Google Scholar]
  • 21.Getz, D., E. Melamud, B. L. Silver, and Z. Dori. 1975. Electronic structure of dioxygen in cobalt (II) oxygen carriers, singlet oxygen or 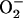Inline graphic? J. Am. Chem. Soc. 97:3846–3847. [Google Scholar]
  • 22.Collman, J. P., R. R. Gagne, C. A. Reed, T. R. Halbert, G. Lang, and W. T. Robinson. 1975. Picket fence porphyrins. Synthetic models for oxygen binding hemoproteins. J. Am. Chem. Soc. 97:1427–1439. [DOI] [PubMed] [Google Scholar]
  • 23.Shaanan, B. 1983. Structure of human oxyhaemoglobin at 2.1 Å resolution. J. Mol. Biol. 171:31–59. [DOI] [PubMed] [Google Scholar]
  • 24.Czerminski, R., and R. Elber. 1991. Computational studies of ligand diffusion in globins.1. Leghemoglobin. Proteins. 10:70–80. [DOI] [PubMed] [Google Scholar]
  • 25.Rovira, C., K. Kunc, J. Hutter, and M. Parrinello. 2001. Structural and electronic properties of cobalt-corrole, cobalt-corrin and cobalt-porphyrin. Inorg. Chem. 40:11–17. [DOI] [PubMed] [Google Scholar]
  • 26.Jensen, K. P., and U. Ryde. 2003. Comparison of the chemical properties of iron and cobalt porphyrins and corrins. Chem. Bio. Chem. 4:413–424. [DOI] [PubMed] [Google Scholar]
  • 27.Rovira, C., K. Kunc, J. Hutter, P. Ballone, and M. Parrinello. 1997. Equilibrium geometries and electronic structure of iron-porphyrin complexes: a density functional study. J. Phys. Chem. A. 101:8914–8925. [Google Scholar]
  • 28.Sigfridson, E., and U. Ryde. 1999. On the significance of hydrogen bonds for the discrimination between CO and O2 by myoglobin. J. Biol. Inorg. Chem. 4:99–110. [DOI] [PubMed] [Google Scholar]
  • 29.Maseras, F. 1998. Binding of dioxygen in a picket-fence porphyrin complex of iron. A theoretical QM/MM study. New J. Chem. 22:327–332. [Google Scholar]
  • 30.Vogel, K. M., P. M. Kozlowski, M. Z. Zgierski, and T. G. Spiro. 1999. Determinants of the FeXO (X = C, N, O) vibrational frequencies in heme adducts from experiment and density functional theory. J. Am. Chem. Soc. 121:9915–9921. [Google Scholar]
  • 31.Scherlis, D. A., and D. A. Estrin. 2001. Hydrogen bonding and O2 affinity of hemoglobins. J. Am. Chem. Soc. 123:8436–8437. [DOI] [PubMed] [Google Scholar]
  • 32.De Angelis, F., A. A. Jarzecki, R. Car, and T. G. Spiro. 2005. Quantum chemical evaluation of protein control over heme ligation: CO/O2 discrimination in myoglobin. J. Phys. Chem. B. 109:3065–3070. [DOI] [PubMed] [Google Scholar]
  • 33.Rovira, C., and M. Parrinello. 2000. Harmonic and anharmonic dynamics of Fe-CO and Fe-O2 in heme models. Biophys. J. 78:93–100. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 34.Vojtechovsky, J., K. Chu, J. Berendzen, R. M. Sweet, and I. Schlichting. 1999. Crystal structures of myoglobin-ligand complexes at near-atomic resolution. Biophys. J. 77:2153–2174. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 35.Hohenberg, P., and W. Kohn. 1964. Inhomogeneous electron gas. Phys. Rev. 136:864–871. [Google Scholar]
  • 36.Kohn, W., and L. J. Sham. 1965. Self-consistent equations including exchange and correlation effects. Phys. Rev. 140:1133–1138. [Google Scholar]
  • 37.Ordejón, P., E. Artacho, and J. M. Soler. 1996. Self-consistent order-N density-functional calculations for very large systems. Phys. Rev. B. 53:10441–10444. [DOI] [PubMed] [Google Scholar]
  • 38.Ordejón, P., E. Artacho, and J. M. Soler. 1996. MRS Symposia Proc. No. 408. Materials Research Society, Pittsburgh, PA.
  • 39.Sánchez-Portal, D., P. Ordejón, E. Artacho, and J. M. Soler. 1997. Density-functional method for very large systems with LCAO basis sets. Int. J. Quantum Chem. 65:453–461. [Google Scholar]
  • 40.Soler, J. M., E. Artacho, J. D. Gale, A. García, J. Junguera, P. Ordejón, and D. Sánchez-Portal. 2002. The SIESTA method for ab initio order-N materials simulation. J. Phys. Condens. Matter. 14:2745–2779. [DOI] [PubMed] [Google Scholar]
  • 41.Ordejón, P. 2000. Linear scaling ab initio calculations in nanoscale materials with SIESTA. Physica Status Solidi B. 217:335–356. [Google Scholar]
  • 42.Perdew, J. P., K. Burke, and M. Ernzerhof. 1996. Generalized gradient approximation made simple. Phys. Rev. Lett. 77:3865–3868. [DOI] [PubMed] [Google Scholar]
  • 43.Ireta, J., J. Neugebauer, and M. Scheffler. 2004. On the accuracy of DFT for describing hydrogen bonds: dependence on the bond directionality. J. Phys. Chem. A. 108:5692–5698. [Google Scholar]
  • 44.Marti, M.A., S. E. Bari, D. A. Estrin, and F. Doctorovich. 2005. Discrimination of nitroxyl and nitric oxide by water-soluble Mn(III) porphyrins. J. Am. Chem. Soc. 127:4680–4684. [DOI] [PubMed] [Google Scholar]
  • 45.Martí, M. A., D. A. Scherlis, F. A. Doctorovich, P. Ordejón, and D. A. Estrin. 2003. Modulation of the NO transeffect in heme proteins: implications for the activation of soluble guanylate cyclase. J. Biol. Inorg. Chem. 8:595–600. [DOI] [PubMed] [Google Scholar]
  • 46.Crespo, A., M. A. Marti, S. G. Kalko, A. Morreale, M. Orozco, J. L. Gelpi, F. J. Luque, and D. A. Estrin. 2005. Theoretical study of the truncated hemoglobin HbN: Exploring the molecular basis of the NO detoxification mechanism. J. Am. Chem. Soc. 127:4433–4444. [DOI] [PubMed] [Google Scholar]
  • 47.Marti, M. A., L. Capece, A. Crespo, F. Doctorovich, and D. A. Estrin. 2005. Nitric oxide interaction with cytochrome c′ and its relevance to guanylate cyclase. Why does the iron histidine bond break? J. Am. Chem. Soc. 127:7721–7728. [DOI] [PubMed] [Google Scholar]
  • 48.Biarnés, X., J. Nieto, A. Planas, and C. Rovira. 2006. Substrate distortion in the Michaelis complex of Bacillus 1,3–1,4-β-glucanase. Insight from first principles molecular dynamics simulations. J. Biol. Chem. 281:1432–1441. [DOI] [PubMed] [Google Scholar]
  • 49.Troullier, N., and J. L. Martins. 1991. Efficient pseudopotentials for plane-wave calculations. Phys. Rev. B. 43:1993–2006. [DOI] [PubMed] [Google Scholar]
  • 50.Kleinman, L., and D. M. Bylander. 1982. Efficacious form for model pseudopotentials. Phys. Rev. Lett. 48:1425–1428. [Google Scholar]
  • 51.Chaudhuri, P., C. N. Verani, E. Bill, E. Bothe, T. Weyhermüller, and K. Wieghardt. 2001. Electronic structure of bis(o-iminobenzosemiquinonato)metal complexes (Cu, Ni, Pd). The art of establishing physical oxidation states in transition-metal complexes containing radical ligands. J. Am. Chem. Soc. 123:2213–2223. [DOI] [PubMed] [Google Scholar]
  • 52.Baker, J., A. Scheiner, and J. Andzelm. 1993. Spin contamination in Density Functional Theory. Chem. Phys. Lett. 216:380–388. [Google Scholar]
  • 53.Montoya, A., T. N. Truong, and A. F. Sarofim. 2000. Spin contamination in Hartree-Fock and Density Functional Theory wavefunctions in modeling of adsorption on graphite. J. Phys. Chem. A. 104:6108–6110. [Google Scholar]
  • 54.Dickinson, L. C., and J. C. W. Chien. 1980. Electron paramagnetic resonance crystallography of 17O-enriched oxycobaltomyoglobin: stereoelectronic structure of the cobalt dioxygen system. Proc. Natl. Acad. Sci. USA. 77:1235–1239. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 55.Rovira, C., and M. Parrinello. 1999. Factors influencing ligand binding properties of heme models: A first principles study of picket-fence and protoheme complexes. Chem. Eur. J. 5:250–262. [Google Scholar]
  • 56.Rovira, C., B. Schulze, M. Eichinger, J. D. Evanseck, and M. Parrinello. 2001. Influence of the heme pocket conformation on the structure and vibrations of the Fe-CO bond in myoglobin. A QM/MM density functional study. Biophys. J. 81:435–445. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 57.Summerville, D. A., R. D. Jones, B. M. Hoffman, and F. Basolo. 1979. Assigning oxidation states to some metal dioxygen complexes of biological interest. J. Chem. Ed. 56:157–163. [Google Scholar]
  • 58.Spartalian, K., G. Lang, J. P. Collman, R. R. Gagne, and C. A. Reed. 1975. Mössbauer spectroscopy of hemoglobin model compounds: evidence for conformational excitation. J. Chem. Phys. 63:5375–5382. [Google Scholar]
  • 59.Mispelter, J., M. Momenteau, D. Lavalette, and J.-M. Lhoste. 1983. Hydrogen-bond stabilization of oxygen in hemoprotein models. J. Am. Chem. Soc. 105:5165–5166. [Google Scholar]
  • 60.Oldfield, E., H. C. Lee, C. Coretsopoulos, F. Adebodum, K. D. Park, S. Yang, J. Chung, and B. Phillips. 1991. Solid state 17O nuclear-magnetic resonance spectroscopic studies of [O2–17O] picket-fence porphyrin, myoglobin, and hemoglobin. J. Am. Chem. Soc. 113:8680–8685. [Google Scholar]
  • 61.Schulze, B., and J. D. Evanseck. 1999. Cooperative role of Arg45 and His64 in the spectroscopic A3 state of carbonmonoxy myoglobin: molecular dynamics simulations, multivariant analysis, and quantum mechanical computations. J. Am. Chem. Soc. 121:6444–6454. [Google Scholar]
  • 62.Lukin, J. A., V. Simplaceanu, M. Zou, N. T. Ho, and C. Ho. 2000. NMR reveals hydrogen bonds between oxygen and distal histidines in oxyhemoglobin·. Proc. Natl. Acad. Sci. USA. 97:10354–10358. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 63.Phillips, S. E. V., and B. P. Schoenborn. 1981. Neutron diffraction reveals oxygen-histidine hydrogen bond in oxymyoglobin. Nature. 292:81–82. [DOI] [PubMed] [Google Scholar]
  • 64.Lee, H. C., M. Ikeda-Saito, T. Yonetani, R. S. Magliozzo, and J. Peisach. 1992. Hydrogen bonding to the bound dioxygen in oxy cobaltous myoglobin reduces the superhyperfine coupling to the proximal histidine. Biochemistry. 31:7274–7281. [DOI] [PubMed] [Google Scholar]
  • 65.Miller, L. M., M. Patel, and M. R. Chance. 1996. Identification of conformational substates in oxymyoglobin through the pH-dependence of the low temperature photoproduct yield. J. Am. Chem. Soc. 118:4511–4517. [Google Scholar]
  • 66.Jameson, G. B., and R. S. Drago. 1985. Role of weak hydrogen bonding in the coordination of dioxygen to hemeproteins and their models. J. Am. Chem. Soc. 107:3017–3020. [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES