Abstract
The structural change of a phospholipid bilayer in water under the action of a shock wave is numerically studied with unsteady nonequilibrium molecular dynamics simulations. The action of shock waves is modeled by the momentum change of water molecules, and thereby we demonstrate that the resulting collapse and rebound of the bilayer are followed by the penetration of water molecules into the hydrophobic region of the bilayer. The high-speed phenomenon that occurs during the collapse and rebound of the bilayer is analyzed in detail, particularly focusing on the change of bilayer thickness, the acyl chain bend angles, the lateral fluidity of lipid molecules, and the penetration rate of water molecules. The result shows that the high-speed phenomenon can be divided into two stages: in the first stage the thickness of bilayer and the order parameter are rapidly reduced, and then in the second stage they are recovered relatively slowly. It is in the second stage that water molecules are steadily introduced into the hydrophobic region. The penetration of water molecules is enhanced by the shock wave impulse and this qualitatively agrees with a recent experimental result.
INTRODUCTION
A cell permeabilization technique with shock waves is capable of introducing macromolecules and small polar molecules into the cytoplasm (1–7). This technique is definitely suitable for applications in gene therapy and anticancer drug delivery since shock waves can be focused into specific target sites of patients' bodies noninvasively. The primary concern in recent studies has been the efficiency of macromolecule delivery. Kodama et al. (6) have experimentally demonstrated that the permeability of cell membrane can be enhanced by the increase of the shock wave impulse defined as the time integral of pressure over the shock-pulse duration, irrespective of the peak pressure of the shock wave. The mechanism of the increase in permeability, however, remains unknown and the lack of the knowledge of the phenomenon still prevents the development of the applications mentioned above. Clearly, the microscopic information about the molecular transport across the membrane is required and it will be obtained by molecular dynamics (MD) simulations. In this study, we carry out unsteady nonequilibrium MD simulations of lipid bilayers of cell membranes subjected to the action of shock impulses. We thereby clarify the fundamental and important characteristics of the dynamical process of structural change in lipid bilayers and water penetration into the hydrophobic region of the bilayer.
The biological cell membranes are, as well known, composed of phospholipids, proteins, and carbohydrates, and models describing its structure continue to be revised and refined, beginning from the fluid mosaic model (8) to the lipid rafts microdomain models (9,10). Although the cell membranes in general have such complex structures, the fundamental and common element is the phospholipid bilayer. The method of MD simulations for cell membranes has been developed for the lipid bilayer accordingly. There are a number of important contributions about the numerical methodology, such as the force field (11), the charges of polar molecules (12), the effect of choice of ensembles (13), the treatment of the electrostatic interactions (14), and so on. On the basis of these contributions, works on the molecular transport across the bilayer are being published (15–18). The simulations of pore formation in lipid bilayer have also been performed recently (19–22).
However, we emphasize that much effort has been devoted to the research of an almost static configuration or slow translocation of lipid molecules. Dynamical processes of cell membranes under the action of shock waves have not been investigated with MD simulations so far, to our knowledge. The shock wave is a high pressure wave with a steep wave front that propagates at a supersonic speed, and it passes the cell membrane within a very short time of the order of picoseconds. Therefore, understanding a high-speed phenomenon induced by the interaction of shock waves with cell membranes should be indispensable to the advance of the gene/drug delivery technique with shock waves. We address this challenging problem in this work using unsteady nonequilibrium MD simulations.
METHODS
As mentioned in the Introduction, the interaction of shock waves with cell membranes is a high-speed phenomenon completed in a very short time because the thickness of the membrane is of the order of nanometers and the shock propagation speed is supersonic. Such high-speed phenomena have never been studied in the field of biomolecular dynamics, to our knowledge. Neither the simulation methods nor the analysis tools have been established. We therefore have to construct a new method for modeling of shock waves and new analysis tools. To avoid unexpected difficulties arising from newly introduced techniques, however, we make the most of existing methodology established in the equilibrium simulations with great care.
Lipid bilayer/water system
The simulations here have first been performed with a small bilayer/water system consisting of 32 dipalmitoylphosphatidylcholine (DPPC) lipids and 4800 water molecules in a rectangular simulation box. Thereafter, we have validated the results by conducting further simulations with a larger system of 128 lipids and 19,200 water molecules. This section explains the simulation method of the equilibrium bilayer/water system, which was utilized for an initial condition of shock wave simulation described in subsequent sections.
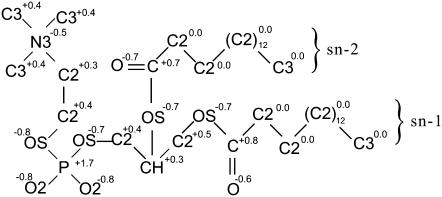
The refined united atom force field (23) with AMBER99 force field (24) was applied to the DPPC lipids. The atomic charges calculated by Chiu et al. (12) were used for DPPC, and they are illustrated in Fig. 1 with the molecular structure and AMBER atom types. The simulation procedure was substantially the same as an already established one (23). For water, the simple point charge model (25) was used. Lennard-Jones interactions were cut off at 1.0 nm, and long-range electrostatic interactions were handled by means of the particle mesh Ewald method (26) with Ewald coefficient 0.275.
FIGURE 1.
Atomic charges and AMBER atom types of DPPC molecule.
The initial configuration of the bilayer/water system for shock wave simulation was prepared in an equilibration simulation (NPT computation), where the temperature and pressure were controlled using the weak coupling algorithm (27) with τT = 0.5 ps, T = 323 K, τp = 1.0 ps, and p = 101.3 kPa. The equations of motion of molecules were integrated employing the leap frog method with time step τ = 2.0 fs, and the three-dimensional periodic boundary conditions were applied. After an ∼8-ns run of equilibration simulation with the SHAKE algorithm (28), we obtained an equilibrated bilayer/water system of volume 7.18 × 5.99 × 17.51 nm in the case of the larger system, where the linear dimension of the simulation box in the z direction normal to the bilayer plane (the xy plane) is 17.51 nm. The volume of the smaller system was 3.77 × 2.72 × 18.32 nm.
Here, we remark that our bilayer/water system included a large water layer of thickness ∼14 nm, whereas the thickness of the bilayer was ∼4 nm. This is because this simulation of shock waves required a large number of water molecules, as explained below. Such a large water layer has also been used by Marrink et al. in an MD simulation of lipid adhesion (29).
Because we are interested in the dynamical process of structural change in bilayer resulting from shock wave irradiation, it may be better to remove the constraint of molecular bond lengths based on the SHAKE algorithm. We therefore continued the equilibrium simulation of the bilayer/water system without using SHAKE and confirmed that the equilibrium configuration of lipid and water molecules remained plausible at least up to 12 ns without SHAKE, as compared with not only earlier numerical results (11,13,14,23) but also experimental ones (30). For example, the average interfacial areas per lipid molecule were 67 Å2 in the larger system and 64 Å2 in the smaller one, and they are included in the range of experimental values from 56 Å2 to 72 Å2 reported in a review article (30). The obtained equilibrium bilayer/water system was utilized for the preparation of the initial configuration for the shock wave simulations.
Modeling of shock waves
In the previous experiment (6), it was shown that the transport of fluorophores across the membranes of leukemia cells is governed by the shock impulse rather than the maximum pressure. The shock impulse per unit area I is defined as
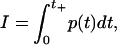 |
(1) |
where t is the time, p(t) is the pressure near the cells in water, and t+ is the positive phase duration of a half cycle of the shock wave (6). The experiment (6) was carried out with different types of shock waves produced by a laser and a shock tube. Their peak pressures and shock-pulse durations were considerably different, and therefore the shock impulse defined by Eq. 1 was introduced to examine the effect of shock waves on the cell permeabilization systematically.
From the definition of impulse, the shock impulse I can be regarded as the increment of momentum of water divided by an area A on which the pressure p(t) is exerted. That is,
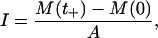 |
(2) |
where M(t) is the momentum of water at time t. At time t = 0, the shock wave did not reach the cells and water ahead of the shock wave was at rest, and hence M(0) = 0. When t = t+, the shock wave passed a small volume of water near the cells and the momentum M(t+) = I × A was transferred to the small volume of water.
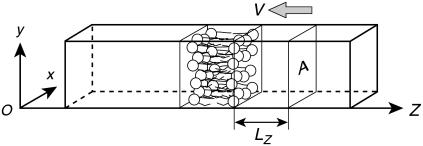
The shock waves in the experiment were pulses with duration times of at least 180 ns, corresponding to the pulse width of ∼270 μm in water. It is impossible or prohibitively expensive to reproduce such shock waves in the simulation box with a periodic boundary condition. In this study, we numerically expressed the shock impulse by the momentum M(t+) of water molecules. More precisely, at the beginning of shock wave simulation, we added the momentum M(t+) = I × A to water molecules in a volume A × LZ adjacent to the bilayer, where the area A is the cross-sectional area normal to the z direction of the simulation box, e.g., A = 7.18 × 5.99 nm = 43.01 nm2 in the larger system, and LZ is the length of the volume in the z direction (see Fig. 2). The choice of LZ is arbitrary, and we put LZ = 4 nm, which is almost equal to the initial thickness of bilayers, because this simulation was focused on the behavior of bilayers with the excess momentum M(t+) added by shock wave. The momentum change of water molecules at the beginning of shock simulation was numerically implemented by the addition of an average velocity V to the thermal velocity of water molecules in the equilibrated bilayer/water system, as shown in Fig. 2. The average velocity V is given by
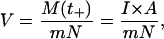 |
(3) |
where m is the weight of a water molecule and N (almost 4000 in the larger system and almost 1000 in the smaller one) is the number of water molecules in the volume A × LZ. The impulse I was increased from 0 to 100 mPa·s at an interval of 2.5 mPa·s, and then V was changed from 0 to 25,600 m/s. Note that the impulse I used in the simulation was very small compared with that in the experiment (6), which was typically 100 Pa·s, although the average velocity V in the simulation appeared to be large. If the impulse I is raised to 100 Pa·s, the required average velocity V is 104 times larger than the sound speed in water. The average velocity V corresponds neither to the sound speed of liquid water nor to the propagation speed of the shock wave. It just represents the increase of momentum of water molecules due to the shock wave. The modeling of shock waves by the impulse makes the qualitative comparison possible between the numerical results in this work and the previous experimental ones.
FIGURE 2.
Schematic of the initial configuration of shock wave simulation. The average velocity V defined by Eq. 3 is added to water molecules in a volume A × LZ, where A is the cross-sectional area of simulation box, and LZ = 4 nm. The NVE MD simulations were performed from this initial configuration.
Unsteady nonequilibrium simulation
We performed constant-volume MD simulation (NVE simulation) without using the control of temperature and pressure and the SHAKE algorithm from the initial configuration shown in Fig. 2. The periodic boundary conditions were applied in the three directions. The time step for integration of equations of motion was varied from τ = 2.0 fs to 0.78 fs according to the size of V to avoid the excess approach of molecules with large velocities. The AMBER 7 set of programs (31) was used for computations.
Owing to the periodic boundary conditions, the simulations should be terminated at the time when the effect of the shock impulse reached the boundary at the opposite side of the simulation box. To simulate the essential part of structural changes of the bilayer before the termination of the simulation, sufficiently thick water regions were required in both sides of the bilayer in the simulation box. We therefore used the bilayer/water system with a large water layer of thickness ∼14 nm.
ANALYSIS
The conspicuous structural change of bilayers in the dynamical process under the action of the shock impulse was the collapse and rebound of bilayers. In this study, the collapse and rebound of bilayers were analyzed by evaluating the thickness of bilayers, which was defined as the distance between phosphorous atoms in the headgroups of lipid molecules in upper and lower sides of bilayer. This definition is reasonable because two peaks in the electron density profile across the bilayer correspond to the locations of phosphorous atoms (23).
In the collapse and rebound stages of bilayers, the ordering in the tails (acyl chains) of lipid molecules was considerably different from that in the equilibrium state. The order parameter SCD (11,14,32) is widely known to be a useful measure for the ordering of lipid molecules in equilibrium states, and usually SCD is evaluated in a long-time average. In the analysis of collapsing and rebounding bilayers, the application of long-time averages should be bypassed, and therefore we used an averaged instantaneous order parameter ŜCD defined as
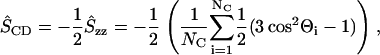 |
(4) |
where Θi is the angle between the axis of the ith molecular axis and the bilayer normal (the z axis) and NC (= 28) is the number of carbons in both sn-1 and sn-2 chains (see Fig. 1). The angle Θis were evaluated from the instantaneous configurations of lipid molecules. By definition, in the equilibrium states, −ŜCD is equal to the average of the usual −SCD over all carbons in acyl chains, the value of which is estimated as ∼0.16 from an earlier numerical result (11).
The fluidity of lipid molecules within the bilayer plane (the xy plane) has often been studied by means of the diffusion coefficient in the equilibrium MD simulations (33). However, the diffusion coefficient was not an appropriate measure of the fluidity in a high-speed phenomenon in the unsteady and nonequilibrium state. To quantify the lateral fluidity of lipids in the bilayer plane in unsteady states, we introduced an accumulated lateral displacement ALD defined as
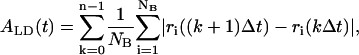 |
(5) |
where ri is the distance from an origin of the xyz coordinates to the projection of the position of mass center of the ith lipid molecule onto the xy plane, NB (= 32 or 128) is the number of lipid molecules in the bilayer, Δt (= 8τ) is a time interval for producing a configuration frame, k is the frame number, and n = t/Δt. Note that ALD is independent of the choice of the origin of the coordinate system, and it increases with increase in the movement of lipid molecules in the bilayer. We also examined the growth rate of ALD, defined as dALD/dt, which should be a constant in an equilibrium state.
The transport of water molecules into the bilayer was the most important phenomenon in the results of these simulations. It has been suggested experimentally (34,35) and confirmed numerically (11,13) that very few water molecules exist beyond the carbonyl group in the sn-1 chain (see Fig. 1) in equilibrium states. Accordingly, when a water molecule entered a hydrophobic region between the carbonyl groups in sn-1 chains in upper and lower sides of bilayers in the simulation, we decided that the water molecule was transported into the bilayer.
RESULTS AND DISCUSSION
Collapse and rebound of bilayers
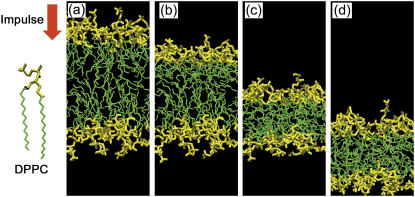
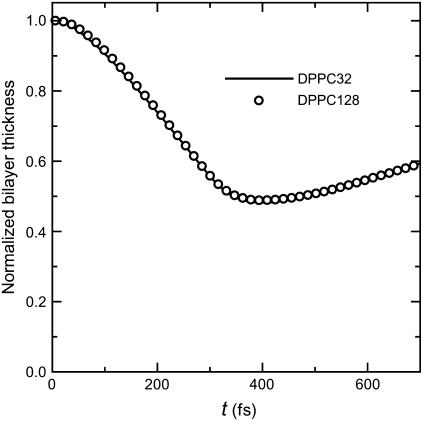
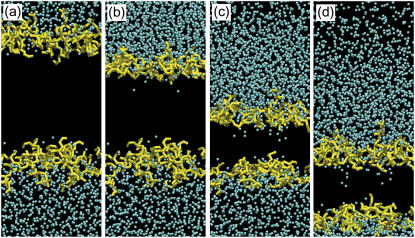
Fig. 3 is a series of snapshots in a typical result of shock wave simulation for I = 50 mPa·s and V = 12,800 m/s, where the collapse and rebound of bilayers are clearly shown. The excess momentum of shock impulse propagated downwards, first pushing down the upper layer and keeping the lower layer intact (see Fig. 3, b and c). Finally, the excess momentum was transferred to the lower layer and it was also pushed down (Fig. 3 d). At that time, since the excess momentum had already passed the upper layer, the force pushing it down became weak, and the rebound stage set in. In this case, the simulation was terminated at t = 700 fs. The change of bilayer thickness is shown in Fig. 4. One can see that it decreased to almost half of the initial value (4 nm) at ∼350 fs from the instant of shock impulse impact, and then it rebounded slowly. The numerical result in the smaller system completely agrees with that in the larger system.
FIGURE 3.
A series of snapshots of the collapse and rebound of lipid bilayer under the action of shock impulse of I = 50 mPa·s. The impulse was applied downwards. The headgroups of DPPC are shown in yellow and the acyl chains in green. Water molecules are not shown for clarity of presentation. (a) Equilibrium state; (b) 0.15 ps after the application of shock impulse. The upper layer began to move downwards; (c) 0.30 ps. The lower layer began to move; (d) 0.45 ps. The rebound stage of bilayer. The snapshots were made with the VMD program (Humphrey, W., Dalke, A., and Schulten, K. 1996. J. Mol. Graph. Model. 14:33–38).
FIGURE 4.
The evolution of bilayer thickness normalized by its initial value (4 nm) at I = 50 mPa·s. The solid curve represents the result with the smaller system (32 lipids) and the open circles that with the larger system (128 lipids).
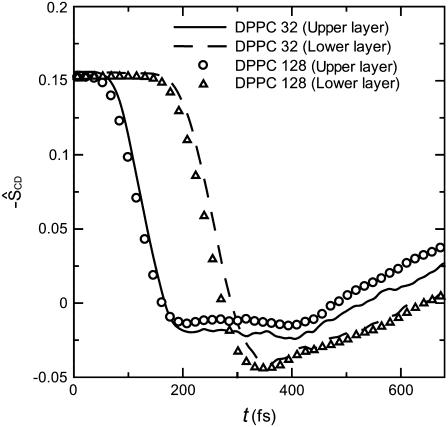
The thickness of a bilayer is closely related to the length of acyl chains in the bilayer. The change of chain length can be characterized by the averaged instantaneous order parameter ŜCD, because the chain length becomes small if the disorder of chain bend angles increases. In Fig. 5, we present the temporal changes of −ŜCDs of the upper and lower layers separately for the case of I = 50 mPa·s. Before the beginning of collapse, both −ŜCDs were equal to 0.16 as expected from knowledge of the equilibrium state (11). As the shock impulse propagated downwards in the bilayer, first the −ŜCD of the upper layer and then that of the lower layer began to decrease, and the time lag was ∼0.1 ps, which corresponded to the time that the shock impulse passed the bilayer. The two −ŜCDs were rapidly reduced until reaching their minimum values, and the following rebound process was relatively slow. From the comparison with Fig. 4, it is immediately realized that the change of bilayer thickness was due to the change of chain bend angles.
FIGURE 5.
The temporal change of averaged instantaneous order parameter ŜCD defined by Eq. 4 at I = 50 mPa·s.
Fluidity of lipid molecules
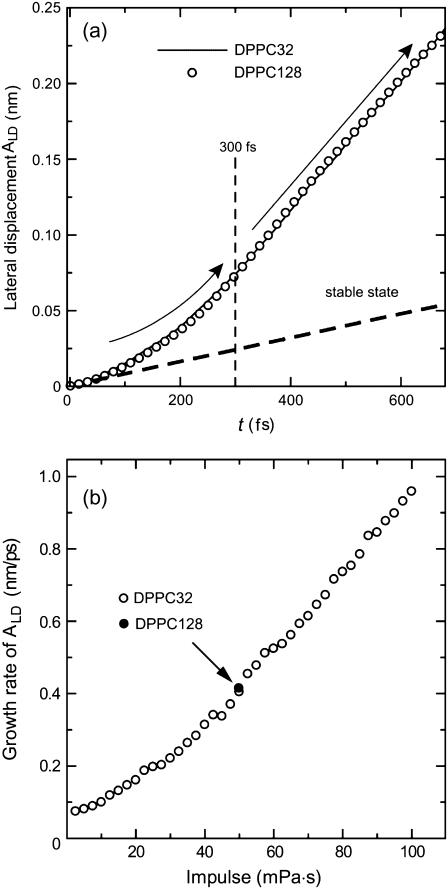
Fig. 6 a shows the temporal evolution of the accumulated lateral displacement ALD, defined by Eq. 5, for the case of I = 50 mPa·s. In the stable state (equilibrium state), it constantly grows with time, as indicated by a bold broken line in the figure. On the other hand, the growth of ALD in the shock wave simulation was composed of two stages: in the first stage from t = 0 to t = 300 fs, the growth rate dALD/dt gradually increased, and in the second stage after t = 300 fs, it was almost constant, as indicated by thin solid curves with arrows. These two stages precisely agreed with the collapse and rebound stages of bilayers shown in Figs. 3–5. In particular, it is worth noting that the growth rate was hardly weakened in the rebound stage.
FIGURE 6.
(a) Accumulated lateral displacement ALD defined by Eq. 5 at I = 50 mPa·s. The behavior of ALD is explained by the solid curves with arrows. (b) The change of the growth rate dALD/dt in the rebound stage for varying shock impulse.
Fig. 6 b shows that the growth rate dALD/dt in the second stage was an increasing function of shock impulse. In the equilibrium state it is not 0 but ∼0.1 nm/ps (see Fig. 6 a). However, despite the nonzero growth rate, very few water molecules enter the hydrophobic region in the equilibrium state, as mentioned before. Therefore, the continuance of high fluidity, i.e., the large growth rate for some period, seems to play an essential role for the penetration of water molecules because the growth rate can be regarded as a measure of the lateral fluidity of lipid molecules.
Water penetration into the hydrophobic region
The application of shock impulse to bilayer induced the penetration of water molecules in the hydrophobic region of the bilayer. In the following, we demonstrate how the water molecules penetrated into the bilayer and discuss this important phenomenon.
Fig. 7 is a series of snapshots for the same result as that shown in Fig. 3 (in a slight close-up). In the figure, acyl chains are eliminated and water molecules are indicated by blue spots. The penetration of water molecules into the hydrophobic region of the bilayer is shown clearly. Note that, as can be seen from Fig. 7 a, even in the equilibrium state (before the arrival of the shock impulse), several water molecules exist near the lipid headgroups shown in yellow. However, they are outside the hydrophobic region between the carbonyl groups in sn-1 chains in upper and lower sides of the bilayer, and they cannot enter the hydrophobic region without the action of the shock impulse in the timescale of MD simulations.
FIGURE 7.
A series of snapshots of water penetration for the same result as that shown in Fig. 3. Water molecules are signified by blue spots, and acyl chains are eliminated. (a) Equilibrium state; (b) 0.15 ps. Some water molecules were carried into the hydrophobic region; (c) 0.30 ps; (d) 0.45 ps. Even in the rebound stage, water molecules still penetrated into the hydrophobic region.
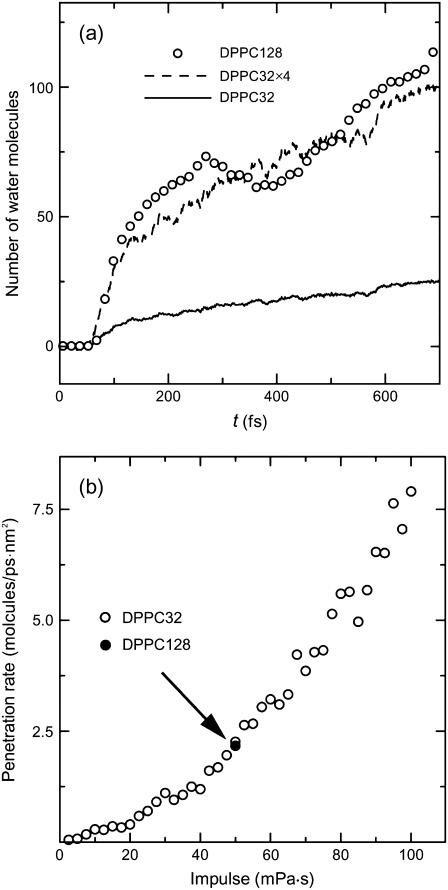
We plot the number of water molecules in the hydrophobic region in Fig. 8 a for the case of I = 50 mPa·s. Except for the beginning of the collapse stage, the number of water molecules increased with time at a constant rate (100 molecules/ps) even after the rebound stage began (300 fs). This means that the rebound stage is more significant for water penetration than the collapse stage, although the structural change (bilayer shrinkage and acyl chain disorder) occurs much more violently in the collapse stage. The number of water molecules in the hydrophobic region in the larger system of 128 lipids is four times as large as that in the smaller system of 32 lipids, as expected.
FIGURE 8.
(a) The number of water molecules in the hydrophobic region at I = 50 mPa·s. The broken line denotes the penetration rate except for the beginning of collapse of bilayer. (b) The penetration rate of water molecules versus shock impulse.
In Fig. 8 b, we illustrate how the number of penetrated water molecules increased with the increase in shock impulse. The ordinate in the figure represents the number of water molecules in the hydrophobic region at the instant of termination of simulation divided by the cross-sectional area (A = 43.01 nm2 in the larger system and 10.25 nm2 in the smaller one) and the simulation time. The rate of water penetration in the rebound stage can be estimated as ∼2.5 molecules/ps·nm2 in the case of I = 50 mPa·s and it exceeded 7.5 molecules/ps·nm2 in the case of I = 100 mPa·s. We remark that the trend observed in Fig. 8 b is similar to that of the growth rate of ALD shown in Fig. 6 b. That is, as the shock impulse increases, the lateral fluidity of lipid molecules increased and so did the number of penetrated water molecules.
As shown in Fig. 8 b, the number of penetrated water molecules increased with increasing shock impulse. This qualitatively agrees with the previous experiment (6), although there were a few differences: in the experiment, calcein (622 Da) and fluorescein isothiocyanate dextran (71.6 kDa) were delivered into the cells by the shock impulse of 100 Pa·s, whereas in the simulation, water (18 Da) penetrated into the bilayer by the impulse of at most 100 mPa·s. This may be a reflection of the fact that the transport of large molecules across cell membranes requires a large amount of impulse.
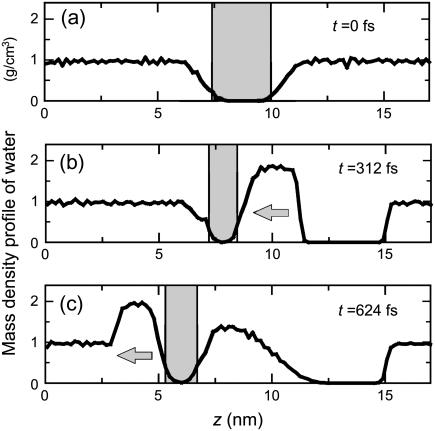
The mass density profile of water molecules in the case of I = 50 mPa·s is illustrated in Fig. 9, where Fig. 9 a shows the initial profile and the shading indicates the hydrophobic region. From the figure, it is clear that water molecules are carried into the hydrophobic region (see Fig. 7) and the shrinkage and recovery of the hydrophobic region are induced by high density water. An empty region behind the high density water (12 nm < z < 15 nm) is caused by the velocity difference in the initial condition.
FIGURE 9.
The mass density profiles for the case of I = 50 mPa·s in the larger system of 128 lipids. The mass density is evaluated by counting the number of water molecules in a slab of width 1.74 Å. The direction of propagation of shock wave is indicated by arrows. (a) The initial profile. (b) At t = 312 fs, a high density water region appears near the bilayer and water molecules have already been transported into the hydrophobic region indicated by the shading. (c) At t = 628 fs, a high density water region appears in the opposite side of the bilayer.
These shock wave simulations were limited to a relatively small bilayer/water system. Nevertheless, as a result of careful simulations and analyses, we clarified several important features in the dynamical process of lipid bilayers under the action of shock impulses, which had never been investigated, to our knowledge, from the molecular point of view. Now, on the basis of these numerical results, we propose a possible mechanism of molecular transport of external macromolecules across the cell membrane by the shock wave. Unlike the penetration of water molecules, the transport of macromolecules requires a transient pore filled with water in the cell membrane, as several authors have considered (5,19–22). As shown in these simulations, the action of the shock impulse results in the penetration of water molecules and is not directly connected to the pore formation. We predict that the inclusion of a large number of water molecules in the hydrophobic region of the bilayer leads to the spontaneous pore formation in the cell membrane after the shock wave has gone. This will be demonstrated in a forthcoming work.
SUMMARY
Unsteady and nonequilibrium MD simulations of the interaction of a single shock impulse with a lipid bilayer were performed. The detailed picture of the structural change in the bilayer was clarified to be composed of the two stages, the collapse and rebound stages. The change of the bilayer thickness, the distribution of chain bend angles, the lateral fluidity of lipid molecules, and the subsequent water penetration into the hydrophobic region were examined. These structural changes depended on the intensity of the shock impulse, and the results showed the qualitative agreement with those in the previous experiment. We found that the lateral fluidity of lipid molecules continued to be large for some period in the rebound stage without being weakened, and it is in this rebound stage that water molecules are transported into the hydrophobic region of the bilayer at a constant rate for a given shock impulse.
Acknowledgments
T.K. was supported by grants from Special Coordination Funds for Promoting Science and Technology (MEXT), Grant-in-Aid for Scientific Research on Priority Areas, MEXT (17012002, 18014002), Grant-in-Aid for Exploratory Research, JSPS (18650140), Grant-in-Aid for Scientific Research (B), JSPS (17300168), and Research on Advanced Medical Technology, Health Labor Sciences Research Grant, the Ministry of Health, Welfare and Labor, Japan (H17-nano-006).
References
- 1.Gambihler, S., and M. Delius. 1992. Transient increase in membrane permeability of L1210 cells upon exposure to lithotripter shock waves in vitro. Naturwissenschaften. 79:328–329. [DOI] [PubMed] [Google Scholar]
- 2.Doukas, A. G., D. J. McAuliffe, and T. J. Flotte. 1993. Biological effects of laser-induced shock waves: structural and functional cell damage in vitro. Ultrasound Med. Biol. 19:137–146. [DOI] [PubMed] [Google Scholar]
- 3.Gambihler, S., M. Delius, and J. W. Ellwart. 1994. Permeabilization of the plasma membrane of L1210 mouse leukemia cells using lithotripter shock waves. J. Membr. Biol. 141:267–275. [DOI] [PubMed] [Google Scholar]
- 4.Delius, A., and G. Adams. 1999. Shock wave permeabilization with ribosome inactivating proteins: a new approach to tumor therapy. Cancer Res. 59:5227–5232. [PubMed] [Google Scholar]
- 5.Rosenthal, I., J. Z. Sostaric, and P. Riesz. 2004. Sonodynamic therapy—a review of the synergistic effects of drugs and ultrasound. Ultrason. Sonochem. 11:349–363. [DOI] [PubMed] [Google Scholar]
- 6.Kodama, T., M. R. Hamblin, and A. G. Doukas. 2000. Cytoplasmic molecular delivery with shock waves: importance of impulse. Biophys. J. 79:1821–1832. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Kodama, T., A. G. Doukas, and M. R. Hamblin. 2002. Shock wave-mediated molecular delivery into cells. Biochim. Biophys. Acta. 1542:186–194. [DOI] [PubMed] [Google Scholar]
- 8.Singer, S. J., and G. L. Nicholson. 1972. The fluid mosaic model of the structure of cell membranes. Science. 175:720–731. [DOI] [PubMed] [Google Scholar]
- 9.Simons, K., and E. Ikonen. 1997. Functional rafts in cell membranes. Nature. 387:569–572. [DOI] [PubMed] [Google Scholar]
- 10.Edidin, M. 2003. The state of lipid rafts: from model membranes to cells. Annu. Rev. Biophys. Biomol. Struct. 32:257–283. [DOI] [PubMed] [Google Scholar]
- 11.Berger, O., O. Edholm, and F. Jahnig. 1997. Molecular dynamics simulations of a fluid bilayer of dipalmitoylphosphatidylcholine at full hydration, constant pressure, and constant temperature. Biophys. J. 72:2002–2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Chiu, S. W., M. Clark, V. Balaji, S. Subramaniam, H. L. Scott, and E. Jakobsson. 1995. Incorporation of surface tension into molecular dynamics simulation of an interface: a fluid phase lipid bilayer membrane. Biophys. J. 69:1230–1245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Shinoda, W., N. Namiki, and S. Okazaki. 1997. Molecular dynamics study of a lipid bilayer: convergence, structure, and long-time dynamics. J. Chem. Phys. 106:5731–5743. [Google Scholar]
- 14.Patra, M., M. Karttunen, M. T. Hyvonen, E. Falck, P. Lindqvist, and I. Vattulainen. 2003. Molecular dynamics simulations of lipid bilayers: major artifacts due to truncating electrostatic interactions. Biophys. J. 84:3636–3645. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Tieleman, D. P., and J. Bentz. 2002. Molecular dynamics simulation of the evolution of hydrophobic defects in one monolayer of a phosphatidylcholine bilayer: relevance for membrane fusion mechanisms. Biophys. J. 83:1501–1510. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Zhu, F., E. Tajkhorshid, and K. Schulten. 2002. Pressure-induced water transport in membrane channels studied by molecular dynamics. Biophys. J. 83:154–160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Ulander, J., and A. D. J. Haymet. 2003. Permeation across hydrated DPPC lipid bilayers: simulation of the titrable amphiphilic drug valproic acid. Biophys. J. 85:3475–3484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Bemporad, D., C. Luttmann, and J. W. Essex. 2004. Computer simulation of small molecule permeation across a lipid bilayer: dependence on bilayer properties and solute volume, size, and cross-sectional area. Biophys. J. 87:1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Tieleman, D. P. 2004. The molecular basis of electroporation. BMC Biochem. 5:10:1–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Leontiadou, H., A. E. Mark, and S.-J. Marrink. 2004. Molecular dynamics simulations of hydrophilic pores in lipid bilayers. Biophys. J. 86:2156–2164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Tarek, M. 2005. Membrane electroporation: a molecular dynamics simulation. Biophys. J. 88:4045–4053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Gurtovenko, A. A., and I. Vattulainen. 2005. Pore formation coupled to ion transport through lipid membranes as induced by transmembrane ionic charge imbalance: atomistic molecular dynamics study. J. Am. Chem. Soc. 127:17570–17571. [DOI] [PubMed] [Google Scholar]
- 23.Smondyrev, A. M., and M. L. Berkowitz. 1999. United atom force field for phospholipid membranes: constant pressure molecular dynamics simulation of dipalmitoylphosphatidicholine/water system. J. Comput. Chem. 20:531–545. [Google Scholar]
- 24.Wang, J. M., P. Cieplak, and P. A. Kollman. 2000. How well does a restrained electrostatic potential (RESP) model perform in calculating conformational energies of organic and biological molecules? J. Comput. Chem. 21:1049–1074. [Google Scholar]
- 25.Berendsen, H. J. C., J. P. M. Postma, W. F. van Gunsteren, and J. Hermans. 1981. Interaction models for water in relation to protein hydration. In Intermolecular Forces. B. Pullman, editor. Reidel Publishing Company, Dordrecht, The Netherlands. 331–342.
- 26.Essmann, U., L. Perera, M. L. Berkowitz, T. Darden, H. Lee, and L. G. Pedersen. 1995. A smooth particle mesh Ewald method. J. Chem. Phys. 103:8577–8593. [Google Scholar]
- 27.Berendsen, H. J. C., J. P. M. Postma, W. F. van Gunsteren, A. DiNola, and J. R. Haak. 1984. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 81:3684–3690. [Google Scholar]
- 28.Ryckaert, J. P., G. Ciccotti, and H. J. C. Berendsen. 1977. Numerical integration of the Cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes. J. Comput. Phys. 23:327–341. [Google Scholar]
- 29.Marrink, S.-J., O. Berger, P. Tieleman, and F. Jähnig. 1998. Adhesion forces of lipids in a phospholipid membrane studied by molecular dynamics simulations. Biophys. J. 74:931–943. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Nagle, J. F., and S. Tristram-Nagle. 2000. Structure of lipid bilayers. Biochim. Biophys. Acta. 1469:159–195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Pearlman, D. A., D. A. Case, J. W. Caldwell, W. S. Ross, T. E. Cheatham, S. Debolt, D. Ferguson, G. Siebel, and P. Kollman. 1995. AMBER, a package of computer-programs for applying molecular mechanics, normal-mode analysis, molecular dynamics and free-energy calculations to simulate the structural and energetic properties of molecules. Comput. Phys. Commun. 91:1–41. [Google Scholar]
- 32.Egberts, E., and H. J. C. Berendsen. 1988. Molecular dynamics simulation of a smectic liquid crystal with atomic detail. J. Chem. Phys. 89:3718–3732. [Google Scholar]
- 33.Almeida, P. F. F., and W. L. C. Vaz. 1995. Lateral diffusion in membranes. In Handbook of Biological Physics, Vol. 1. Structure and Dynamics of Membrane. R. Lipowsky and E. Sackmann, editors. Elsevier, Amsterdam. 305–357.
- 34.Zaccai, G., J. K. Blasie, and B. P. Schoenborn. 1975. Neutron diffraction studies on the location of water in lecithin bilayer model membranes. Proc. Natl. Acad. Sci. USA. 72:376–380. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Büldt, G., H. U. Gally, and J. Seelig. 1979. Neutron diffraction studies on phosphatidylcholine model membranes. J. Mol. Biol. 134:673–691. [DOI] [PubMed] [Google Scholar]