Abstract
It is commonly known that the amino acid residue tryptophan and its side-chain analogs, e.g., indole, are strongly attracted to the interfacial region of lipid bilayers. Phenylalanine and its side-chain analogs, e.g., benzene, do not localize in the interface but are distributed throughout the lipid bilayer. We use molecular dynamics to investigate the details of indole and benzene localization and orientation within a POPC bilayer and the factors that lead to their different properties. We identify three sites in the bilayer at which indole is localized: 1), a site in the interface near the glycerol moiety; 2), a weakly bound site in the interface near the choline moiety; and 3), a weakly bound site in the center of the bilayer's hydrocarbon core. Benzene is localized in the same three positions, but the most stable position is the hydrocarbon core followed by the site near the glycerol moiety. Transfer of indole from water to the hydrocarbon core shows a classic hydrophobic effect. In contrast, interfacial binding is strongly enthalpy driven. We use several different sets of partial charges to investigate the factors that contribute to indole's and benzene's orientational and spatial distribution. Our simulations show that a number of electrostatic interactions appear to contribute to localization, including hydrogen bonding to the lipid carbonyl groups, cation-π interactions, interactions between the indole dipole and the lipid bilayer's strong interfacial electric field, and nonspecific electrostatic stabilization due to a mismatch in the variation of the nonpolar forces and local dielectric with position in the bilayer.
INTRODUCTION
It has been known for some time that the amino acid tryptophan (trp) prefers to exist in the interfacial region of lipid bilayers, the ∼15-Å-thick region between the hydrocarbon core and the aqueous solvent (1). This preference was apparent in the earliest structures of intrinsic membrane proteins solved to atomic resolution (2), and it has been confirmed by statistical analyses of known and putative membrane-spanning elements (3–5). Transfer free energies measured using small peptides (1) indicate that trp favors the interfacial region over aqueous solvent more strongly than any other natural amino acid. Trp residues also strongly disfavor the hydrocarbon core. When placed into the center positions of hydrophobic membrane-spanning helices, trp residues can pull these helices out of transbilayer orientations and into interfacial orientations (6,7). This same repulsion is believed responsible for the structural reorganization observed when a gramicidin A dimer is transferred from a bulk nonpolar solvent such as octanol to a lipid bilayer (8).
Measurements of the effective hydrophobic length of engineered membrane-spanning α-helical peptides (9–11) and NMR studies of trp side-chain analogs such as indole (12–14) have identified the preferred interfacial location of the trp side chain and indole: both prefer to locate at the boundary of the hydrocarbon core, near the glycerol region of the membrane lipids. Recently, NMR data have also provided evidence for a second weaker binding location near the choline moiety of phosphocholine lipids (14). This weaker binding location contains ∼1/3 of the indole molecules residing in phosphocholine bilayers at the studied concentration.
Although fluorescence quenching experiments have shown that many aromatic compounds adopt locations within lipid bilayers that are similar to indole (15), statistical studies (3–5) and protein engineering studies of membrane-spanning α-helices (6) have shown that phenylalanine (phe) and, by inference, side-chain analogs of phe such as benzene are not strongly localized; i.e., they are nearly as likely to be found in the hydrocarbon core of a lipid bilayer as in the interfacial region.
The first computational study of indole localization used an implicit Langevin dipole model of the bilayer and surrounding solvent (16). This simulation reproduced indole's preference for localization in the interface, showing that localization can be qualitatively reproduced using relatively simple descriptions of the electrostatic environment—molecular details of the lipid may not be necessary. This conclusion is supported by the ability of simple electrostatic models based on the generalized Born approximation to exhibit interfacial localization of indole (17). Previous all-atom representations of the lipid bilayer and aqueous solvent did not observe interfacial localization (18), but other all-atom simulations have observed favorable enthalpic interactions of the trp side chain with phosphatidylcholine headgroups (19). In this work, we show that an all-atom force field qualitatively reproduces the known facts about indole and benzene partitioning and localization. Recent simulations by McCallum and Tieleman (20), using a different lipid and small molecule force field, have observed similar results suggesting that most modern force fields are able to reproduce the general aspects of aromatic-lipid interactions.
Many factors may contribute to indole's interfacial localization such as:
The hydrophobic effect, which favors exclusion of indole from aqueous solvent. This is especially strong in trp, which has the most surface area of any natural amino acid.
The lipophobic effect, the analog of the hydrophobic effect that describes the solvation of uncharged solutes by the bilayer lipids. Trp's rigid planar shape may favor localization due to compatibility with the liquid-crystalline-like order of the lipid bilayer, which varies strongly with depth in the hydrocarbon core. The hydrophobic and lipophobic effects together constitute the nonpolar forces on indole and benzene.
Hydrogen bonding between the N1 proton of indole (Fig. 1) and the lipid carbonyl groups located in the glycerol region of the lipid bilayer. Benzene lacks a hydrogen-bond donor, potentially accounting for the difference in the behavior of indole and benzene.
Cation-π interactions (21,22) between indole's aromatic ring and positively charged choline groups in phosphatidylcholine lipids. Cation-π interactions are usually stronger with indole than with benzene (22), which could potentially explain the difference in their behavior in the bilayer. Despite their potential importance, classical additive force fields do a poor job of quantitatively reproducing the strength of cation-π interactions, primarily because they do not include explicit polarizability of the aromatic molecule and its bound cation (23–26).
Electrostatic interactions between the indole dipole moment and the electric field of the bilayer. Phosphocholine bilayers normally have a strong positive electrostatic potential in the hydrocarbon core, which rapidly drops off in the interfacial region (27–33). This strong electrostatic gradient could trap and hold molecules, such as indole, which have a large molecular dipole.
Other nonspecific electrostatic interactions between indole and the lipids and water of the interfacial region. For example, simulations indicate that the interfacial region possesses a large dielectric (34) but a lower surface tension than bulk water (35,36). Molecules with a large surface area might prefer to move into the interfacial region to lower the free energy of nonpolar solvation, but they might be too polar to move into the low dielectric hydrocarbon core region, effectively trapping them in the interfacial region.
FIGURE 1.
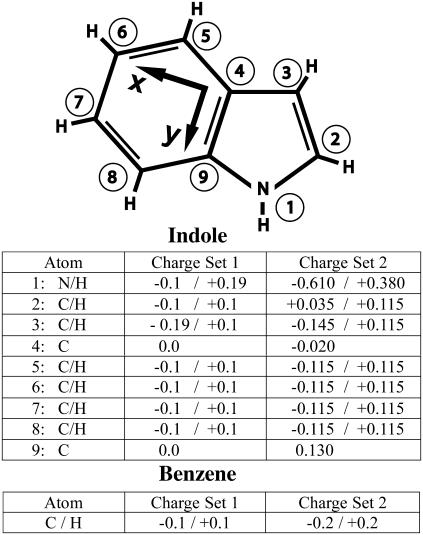
An illustration of the structure of the indole molecule, showing the two sets of partial charges used in our simulations of indole and benzene (in addition to uncharged simulations). Charges are in units of |e|. The partial charges in charge set 1 are adapted from the partial charges in the G96 force field (48) used for the trp side chain. The partial charges in charge set 2 are taken from the ab initio calculations of Woolf et al. (26). The diagram also indicates the local frame used to compute the indole orientation with respect to the bilayer normal (Fig. 8). The z axis is given by the cross product of the x and y axes.
Chemical modifications of both indole and phosphatidylcholine lipid molecules have been used to test the importance of the indole dipole moment and hydrogen bonding to localization. These studies (12–14) suggest that the indole dipole moment and hydrogen bonding do not by themselves result in interfacial localization. The factors primarily responsible for indole localization are still unknown. Measurements of indole in phosphomethanol lipid bilayers suggest that cation-π interactions are involved in localization of indole in the choline region (14).
In this article we provide a demonstration that modern all-atom force fields qualitatively reproduce the distribution and orientation of the small aromatic molecules indole and benzene in a lipid bilayer as a first step toward discriminating among the possible origins of this behavior. Analysis of the temperature dependence of localization is used to probe the contributions of enthalpy and entropy to localization. Transfer of indole to the hydrocarbon core shows a classic hydrophobic effect, but transfer of indole to the interface is strongly enthalpy driven, in agreement with experiments. Using several different charge distributions, we show first that electrostatic interactions are the primary reason for the different behaviors of indole and benzene. We show that small changes in the magnitude of the atomic charges can induce localization and that this localization does not require the molecule to possess a dipole moment. From this information we suggest that interfacial localization can occur because of a simple mismatch in the variation of the nonpolar and local dielectric constants with depth within the lipid bilayer, i.e., a nonspecific electrostatic mechanism, although quantitative agreement appears to require the specific inclusion of the effects of hydrogen bonding, cation-π interactions, or interactions with the membrane dipole potential. These results have important implications for the development of implicit membrane electrostatic models.
METHODS
The initial bilayer structure was generated by selecting a section of previously equilibrated POPC bilayer (44). A short simulation was carried out on this section of POPC bilayer in the NPγT ensemble with harmonic restraints on the lipid atoms. Additional solvent was then added along with several indoles or benzene molecules. All simulations had 13 benzene or indole molecules per unit cell. Each simulation was then equilibrated for a minimum of 10 ns. GROMACS (45) was used for all simulations. The G45A3 force field was used for the POPC lipids (46) with the partial charges of Chiu et al. (47). The force field parameters for indole and benzene were adapted from the G96 (48) parameters for trp and phe. The water model was the single point charge model (49). The relatively small size of the periodic cell was practically necessary to allow us to simulate 200 ns of real time. This was a trade-off between balancing potential finite-sized effects against sampling errors. Although we do not expect significant changes to occur with an increase in the lipid size, simulations are underway to test this hypothesis. Our simulations (data not shown) of a neat POPC bilayer under the same conditions without indole or benzene produced areas per lipid in agreement with experimental values, supporting the validity of the small unit cell.
Three sets of atomic partial charges were used for benzene: in one simulation the partial charges were all 0.0; in a second simulation the partial charges were ±0.1 |e|; in a third simulation the partial charges were ±0.2 |e|. Three sets of atomic partial charges were also used for indole as explained in the text and Fig. 1.
All simulations were carried out at a temperature of 298 K or 350 K, a pressure of 1 bar, and a surface tension of 0 dynes/cm. Hydrogen mass was increased to 4 a.m.u., which may alter the relaxation properties but should not affect the equilibrium properties of the simulation. A 4-fs time step was used with LINCS (50) to restrain all h-bond lengths. particle mesh Ewald (51) was used with a switching function at 12 Å.
All systems were equilibrated for at least 10 ns. Production runs were all 200 ns in length.
Error bars for PMFs were determined through a combination of block averaging and Bayesian analysis. The data were initially blocked into 10 sets of 20 ns each. The number of counts in each bin along the z-position was determined for each of the 10 data sets. For highly sampled regions, the bins contain many counts and the computed PMF values for each of the 10 data sets appear to be drawn from a Gaussian distribution. This allows for relatively easy error estimation provided that the data sets are largely uncorrelated.
For poorly sampled regions, the bins contain few or no counts. In these instances, the PMF computed for some bins can be infinite, making a simple determination of errors as in the highly sampled regions impossible. One possible (but poor) solution is to assume that the error in each bin is a single count and add a single count to each empty bin. This is clearly a poor solution, since it consistently results in the underestimation of both the PMF and the error in the PMF in poorly sampled regions.
Our solution was to estimate the probability distribution for the number of counts in each bin from a Bayesian analysis. Each of the 10 data sets provides a sample from an unknown probability distribution for each bin. The number of counts in each bin was assumed to follow a binomial distribution of values with an unknown probability p for a sample to occur in a given bin. Correlations among counts within a data set were accounted for by assuming that instead of the actual number N of samples, there was a correlation among them reducing the effective number of samples to Neff = N/NC. The numbers of counts in each bin and in total were both reduced by the factor NC. NC was determined from highly sampled regions of the PMF.
To compute the errors, the conditional probability distribution for p given the observed counts in the 10 data sets is required,
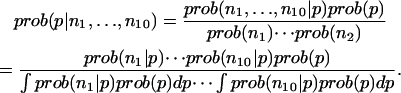 |
The prior distribution of p is assumed to be one for which all PMF values are equally likely. The conditional probabilities in the numerator are computed directly from the binomial distribution. The denominator is a constant that is determined by requiring that
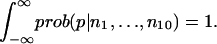 |
The probability distribution for the PMF can be computed from the probability distribution for p, from which mean values as well as confidence intervals are extracted. For computing differences in PMFs, whole probability distributions are used.
RESULTS AND DISCUSSION
Our simulations are carried out on a POPC (1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine) bilayer containing 32 lipid molecules in explicit water and a small number of indole or benzene molecules placed initially in the water region. Simulations are done in the NPγT ensemble at 298 K or 350 K, a pressure of 1 bar, and zero surface tension. Three different partial atomic charges are simulated for both indole and benzene. One simulation of indole and benzene is done with zero partial atomic charges. One simulation of indole and benzene is done with smaller partial atomic charges referred to as charge set 1. A final simulation of indole and benzene is done with larger partial atomic charges referred to as charge set 2. Charge sets 1 and 2 for indole and benzene are shown in Fig. 1. Indole and benzene are simulated at higher temperatures (350 K) to determine the relative contributions of entropy and enthalpy to localization. Further details of the simulation are provided in Methods.
In all simulations, indole and benzene enter the lipid bilayer on a timescale of a few nanoseconds. Indole is relatively insoluble in the aqueous phase. None of the simulations show an appreciable amount of population outside of the bilayer. As expected, benzene is more soluble in the aqueous phase: the simulations using both the smaller and larger partial charges show a significant population in the aqueous solvent.
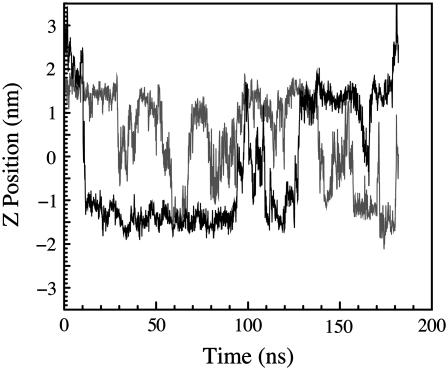
In Fig. 2, we show the trajectories of several indole molecules along the direction of the bilayer normal as a function of time taken from our simulations of indole using charge set 1. Qualitatively similar trajectories are observed for the other indole and benzene simulations with nonzero partial charges, although the amount of localization and the mean waiting time in each region varies by about an order of magnitude. In simulations of indole, the large central barrier results in slow equilibration of the indole population between bilayer leaflets. This appears to be the slowest process in our simulations. After equilibration of the simulation of indole using charge set 2, only 13 events are observed for which an indole crosses from the interfacial region of one leaflet to the interfacial region of another leaflet and remains there stably for more than a nanosecond.
FIGURE 2.
The depth of the indole nitrogen atom relative to the POPC bilayer center as a function of time. Two representative indoles are chosen from 13 indole molecules simulated using charge set 1. This plot illustrates that the indoles localize in different regions of the lipid bilayer; however, the barriers between regions of the bilayer are not so large as to prevent equilibration within the simulation time.
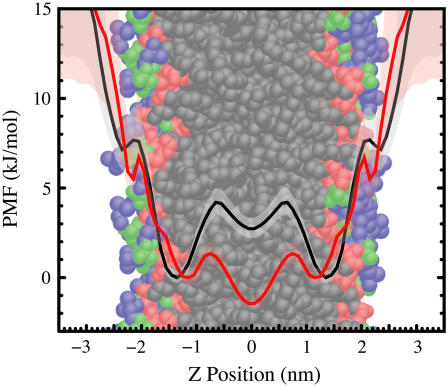
In Fig. 3 we compare the calculated potential of mean force (PMF) for the positioning of indole and benzene relative to the bilayer central plane. The indole nitrogen is used to compute the indole PMF, because of the role that nitrogen has been purported to play in localization. The center of mass of benzene is used to compute its PMF. Charge set 1 is used for these simulations. As for all PMFs, these curves provide relative free energy differences only. We observe three local minima for indole positioning. The dominant binding location is near the glycerol moiety of the bilayer (red-colored lipid region) in agreement with experiments (12–15). Weaker binding locations exist in the hydrocarbon core (black-colored lipid region) and in the vicinity of the choline moiety (blue-colored lipid region). The existence of the choline binding position has been inferred from indole-induced chemical shifts (14), but a hydrocarbon-core binding location has not been experimentally observed. Benzene primarily resides in the hydrocarbon core, in agreement with existing data on the phe residue (4–6). The general agreement between our calculations and experiment as well as the calculations of others (20) support the fundamental suitability of the force fields used in these calculations, although quantitative differences do exist.
FIGURE 3.
The PMF for the depth of the indole nitrogen atom relative to the POPC bilayer center from a simulation using charge set 1 (black curve) and the PMF for the depth of the center of mass of Benzene relative to the POPC bilayer center using charge set 1 (red curve). This figure shows that indole localizes in the interfacial region, but benzene does not localize. The PMFs are vertically offset for clarity. These PMF plots do not provide absolute free energy values anyway—all values are strictly relative. The diffuse background indicates an estimated 95% confidence interval. The PMFs are superimposed on a snapshot of the bilayer colored to show various chemical groups (choline/blue; phosphate/green; glycerol/red; hydrocarbon core/black).
To determine the effects of the indole and benzene charge distributions on their localization, we repeat our simulations using another, larger set of atomic partial charges and using a set of partial charges that are all zero. The larger partial charges for indole (charge set 2) are taken from the ab initio charge fitting of Woolf et al. (26). The larger partial charges for benzene are created by doubling the magnitude of all existing partial charges. These larger sets of partial charges increase all the electrostatic effects: nonspecific electrostatic effects, the strength of hydrogen bonding, cation-π interactions, and interactions between the indole dipole and the membrane dipole potentials.
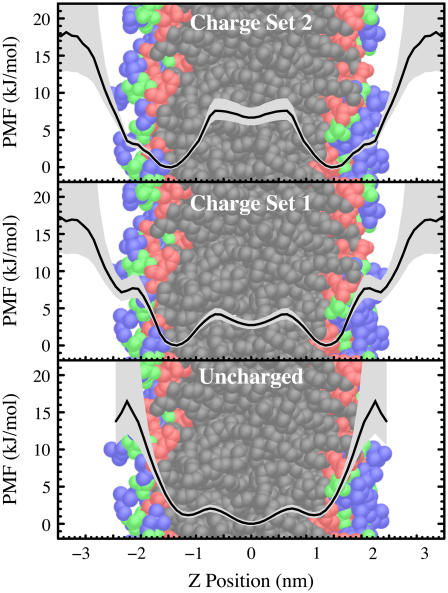
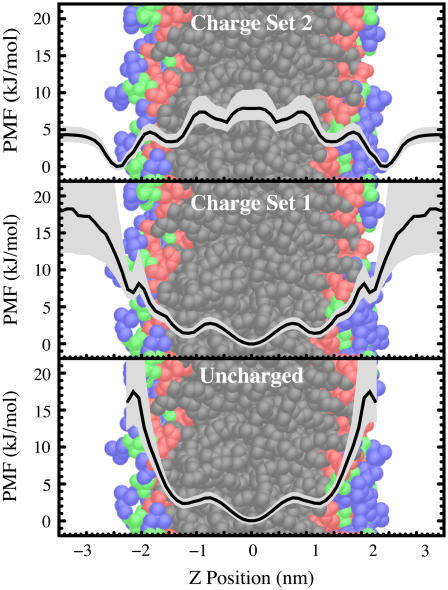
The effects of altering the partial charges on indole are shown in Fig. 4. Uncharged indole molecules primarily reside in the hydrocarbon core. Clearly, nonpolar forces are not the reason for exclusion from the hydrocarbon core. In fact, the distribution of uncharged indole is nearly identical to the distribution of uncharged benzene in the bilayer. Interestingly, there remains a substantial amount of penetration of the uncharged indoles into the interfacial region, a result that is broadly consistent with other calculations (35,36) showing that the surface tension describing the solvation of nonpolar solutes is lower in the interfacial region than in the aqueous phase but contains a strong gradient. Also, there is a clear modulation of the nonpolar forces: the nonpolar forces are not monotonically decreasing throughout the interface. This modulation preserves the distinction of the three binding sites even when the partial charges are all zero.
FIGURE 4.
The PMF for the depth of the indole nitrogen atom relative to the POPC bilayer center as a function of the partial charges on the indole: uncharged (bottom); charge set 1 (middle); and charge set 2 (top). All PMF curves are relative, i.e., they do not show the absolute change in free energy with the change in charge. All curves are vertically adjusted so that the lowest region of the PMF has a value of zero. An estimated 95% confidence interval is indicated by the diffuse backgrounds. This figure suggests that electrostatic interactions are key to the difference in behavior of indole and benzene.
The indole with charge set 2, the larger set of partial charges, shows significant exclusion from the hydrocarbon core and stabilization within the choline region. In light of estimates of the relative populations of the glycerol (∼2/3) and choline (∼1/3) regions (14), this simulation appears to agree most closely with our knowledge of indole positioning. The large value of the PMF in the hydrocarbon core relative to the interface explains why no significant population has been experimentally observed in this region.
Benzene shows similar trends to indole (Fig. 5). An increase in the partial charges results in exclusion of benzene from the hydrocarbon core and stabilization in the interfacial region. Benzene does not have a dipole moment, confirming the experimental evidence that dipolar interactions are not necessary for stabilizing solutes in the interfacial region, although dipolar interactions may quantitatively contribute to localization. The larger set of partial charges for benzene is nonphysical, but is useful for probing the effects of charge in stabilization.
FIGURE 5.
The PMF for the center of mass of the benzene molecule relative to the POPC bilayer center as a function of the partial charges on the benzene: uncharged (bottom); small set of partial charges (middle); and large set of partial charges (top). All PMF curves are relative, i.e., they do not show the absolute change in free energy with the change in charge. All curves are vertically adjusted so that the lowest region of the PMF has a value of zero. An estimated 95% confidence interval is indicated by the diffuse backgrounds. The interfacial localization observed in the simulations using charge set 2 indicates that dipolar interactions are not necessary for localization to occur.
The PMFs presented here are symmetrized. Comparing the symmetrized and unsymmetrized PMFs provides a useful check on the errors in the PMF. In Fig. 6, we compare the symmetrized and unsymmetrized PMFs for indole with charge set 2, which appears to be the simulation with the slowest relaxation behavior. We find good quantitative agreement between the two. Comparison of the other simulations (data not shown) produces agreement that is at least as good as this simulation. In all simulations, the population difference between leaflets results in a total PMF difference of <1 kJ/mol. Surprisingly, we find that the largest discrepancy between symmetrized and unsymmetrized PMFs consistently occurs at a distance of between 2 and 2.5 nm from the bilayer central plane—the choline binding location. This may be an indication that a slowly relaxing process is occurring in this region, perhaps a process requiring substantial lipid headgroup rearrangement.
FIGURE 6.
The difference between our symmetrized data (black curve) and our unsymmetrized data (blue curve) shown for indole using charge set 2, the simulated system with the largest barriers and slowest relaxation. The largest discrepancy between our symmetrized and unsymmetrized PMFs always occurs in the region near the choline groups at a distance of 2 to 2.5 nm from the bilayer center.
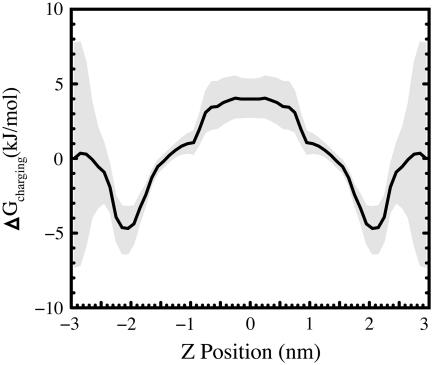
The free energy of charging may be found by taking the difference in the PMFs of the charged and uncharged simulations. The very low amount of indole observed in the aqueous phase makes the calculation of the free energy of charging from zero partial charges to charge sets 1 or 2 problematic. More reliable results arise from altering the charges from set 1 to set 2 (Fig. 7). This free energy difference exhibits only a single minimum in each interfacial region. This indicates that the barrier in the PMF between the choline and glycerol minima is purely nonpolar in nature, and it suggests that similar electrostatic interactions may be responsible for stabilizing indole near both the choline and glycerol moieties.
FIGURE 7.
This figure shows the difference in the PMF for indole using charge set 2 and charge set 1. Because these are PMFs, this difference is only relative. The absolute free energy difference at any one position, as one would get from a free energy perturbation calculation, is unknown. As expected, increasing the partial charges on the indole atoms destabilizes indole in the low dielectric bilayer core relative to water; however, increasing the partial charges also strongly stabilizes indole high in the interfacial region near the choline groups. It does not appear possible to rationalize this strong interfacial stabilization relative to water by modeling the bilayer as a continuum medium with a spatially dependent dielectric constant unless specific indole-lipid interactions or interactions with the lipid dipolar potential are included.
Importantly, the free energy minimum in the interface due to charging cannot be explained with any simple electrostatic continuum model that does not include interactions with the lipid electrostatic field, hydrogen bonding, or cation-π bonding. The total electrostatic contribution to the aqueous solvation of an indole molecule is <50 kJ/mol (37), and transferring an indole molecule from aqueous solvent with a dielectric near 80 to a medium with a higher dielectric would not be expected to produce a stabilizing effect greater than about (50/80) kJ/mol = 0.625 kJ/mol. A careful elucidation of the factors that are most important for localization will be an important input for the further refinement of implicit bilayer models. Although certain effects such as the binding to particular lipid moieties may be difficult to implement within existing implicit models, other effects such as interaction with the membrane dipole potential can be easily incorporated into existing models.
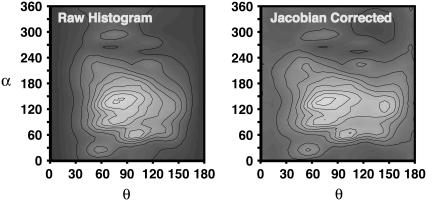
The indoles in the bilayer have certain strongly preferred orientations. The orientation of indoles in the bilayer has been probed by site-specific deuteration of the indole molecules (14) and modeled using a rigid indole molecule with a preferred orientation and wobble. In a similar manner, we characterize the orientational distribution of the indoles by attaching a local coordinate frame (Fig. 1) to the indoles. The bilayer is symmetric under rotations about the bilayer normal, so two angles suffice to characterize the indole distribution: θ, the angle between the z axis of the indole and the bilayer normal; and α, the angle that is assumed when the bilayer normal is projected into the molecular xy plane. Fig. 8 shows the probability density for indoles along these two axes for indoles under charge set 2 averaged over the whole bilayer. Clearly, the orientation is dominated by structures with θ near 90°—indicating that the molecular plane of the indole is orthogonal to the plane of the bilayer—and by structures with α near 110°—an angle for which the indole dipole is aligned in the direction of the electric field in the interface of the bilayer. This suggests a significant quantitative role for the indole dipole moment in localization.
FIGURE 8.
(Left panel) The orientational distribution of indole in the bilayer (computed using charge set 2). The preferred orientation of indole is with the normal to its plane orthogonal to the bilayer normal (θ near 90°) and with its dipole moment aligned with the average electric field of the bilayer in the interface (α near 110° for this set of partial charges). (Right panel) This figure shows the same probability density corrected to eliminate the effects of the Jacobian for solid angle rotations. Weak sampling of orientation of θ near 0° and 180° are real effects and not just artifacts of the Jacobian.
The indole dipole moment cannot, however, be the sole reason for localization because we were able to induce localization in benzene by increasing its partial charges, and it does not possess a dipole moment. Similarly, a generalized Born/surface area model of the bilayer (17) and a Langevin dipole model (16) were able to observe some localization without the inclusion of an average membrane electrostatic potential.
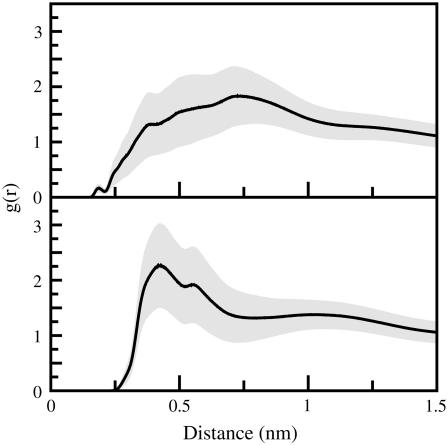
Evidence for cation-π interactions between the lipid choline groups and indoles also exist (Fig. 9), and evidence for hydrogen bonds exists as well (Fig. 10). Clearly both must contribute somewhat to stabilization. Initial simulations of indole with a reduced hydrogen-bonding potential (data not shown) suggest that the interfacial stabilization created by hydrogen bonding to the lipid carbonyl groups is weak, in agreement with most experiments (12–14). The quantitative contribution of cation-π interactions to localization cannot be determined here. The relatively low occupation number for choline in the first solvation shell of indole suggests that it cannot account for localization by itself but does contribute to the effect.
FIGURE 9.
The distribution of phosphate atoms (upper panel) and choline heavy atoms (lower panel) relative to the center of mass of the indole molecules (averaged over all indole molecules in the simulation). Curves are normalized so that the density curves approach the bulk density of phosphate and choline groups within the unit cell.
FIGURE 10.
The number of hydrogen bonds between indole and the lipid carbonyl groups as a function of position in the bilayer for the various charge distributions on indole (uncharged, charge set 1, and charge set 2). As expected the amount of hydrogen bonding increases with the magnitude of the partial charges, suggesting at least a partial role for hydrogen bonding in localization.
Recent simulations of the gramicidin A dimer in POPC and POPE (1-palmitoyl-2-oleoyl-sn-glycero-3-phosphoethanolamine) lipids have investigated the role of cation-π interactions between trp side chains and phospholipid headgroups (38). It was found that, although cation-π interactions are significantly stronger with POPE, they still contribute significantly to interactions with POPC headgroups. Molecular dynamics studies of the interaction between lipids and peptides of the form Ace-WLXLL (39) also observed significant cation-π interactions.
The transfer of indole from the aqueous phase to the interface takes on a different thermodynamic signature than transfer of indole to a bulk nonpolar phase. The transfer to the interface is largely enthalpy driven and opposed by entropy, an effect sometimes referred to as the “nonclassical” hydrophobic effect (1,40). This effect is generic to the transfer of small molecules from the aqueous phase to ordered nonpolar phases (1,40–42), although its origins are unknown. Recent simulations (43) have observed this nonclassical effect for the transfer of hexane to phosphatidylcholine bilayers.
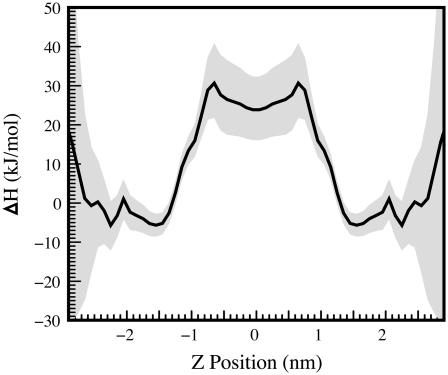
To verify whether this curious aspect of localization is reproduced properly by our force field, we perform simulations at 350 K in addition to our 298 K simulations. The change in the PMF from 298 to 350 K is used to separate the relative energy and enthalpy of the system as a function of indole depth via the Gibbs-Helmholtz equation (Fig. 11). This separation shows that transfers of indole into the hydrocarbon core have a classic hydrophobic character, being entropy driven at temperatures near and below room temperature and opposed by enthalpy. (Another signature of the classic hydrophobic effect is an accompanying increase in the heat capacity, but because we only have data at two temperatures, we cannot reliably estimate the heat capacity change in this instance.) In contrast, transfer of indole to the interface is strongly enthalpy driven and opposed by entropy. Despite our large error bars in the aqueous solvent region, our results are surprisingly in accord with the measured enthalpy for transfer for indole to the bilayer interface: −22.5 kJ/mol (1).
FIGURE 11.
The enthalpy of indole positioning in the bilayer. Enthalpy is determined by assuming a constant enthalpy and entropy as a function of position over a temperature range and fitting the change in the PMF from 298 to 350 (as determined by two separate simulations at those temperatures using charge set 2) to the function ΔG = ΔH − TΔS. As expected, we find that transfer of an indole molecule from water to the interface is an enthalpy-driven process, whereas transfer from water to the bilayer interior is an entropy-driven process.
In conclusion, we have provided an unbiased demonstration of indole localization using explicitly represented aqueous solvent and bilayer. In general agreement with experiment, we observe that indole localizes whereas benzene does not. The existing force fields appear to do a good job in reproducing the behavior of indoles and benzenes in bilayers. Using the ab initio charges of Woolf et al. (26), the population and orientation of indole in simulation appear to closely match the distribution inferred via NMR measurements. The “nonclassical” hydrophobic characteristics of interfacial binding are also accurately reproduced.
The amount of localization in both benzene and indole can be varied by small changes in the partial charges of each molecule. Increasing the partial charges will cause benzene to localize and indole to localize more strongly; decreasing the partial charges will result in both benzene and indole primarily residing in the hydrocarbon core of the lipid bilayer. Localization does appear to have some dependence on nonspecific electrostatic effects, cation-π interactions, dipolar interactions between the indole and the bilayer, and hydrogen bonding to the bilayer carbonyl groups. A detailed quantitative description of localization will most likely require the inclusion of all these effects.
Acknowledgments
We thank Rafael Brüschweiler and Klaus Gawrisch for helpful advice. All calculations were performed on the Anfinsen Cluster housed in the FSU School of Computational Science.
Support for K.E.N. was provided by the Florida State University Howard Hughes Undergraduate Program in Mathematical and Computational Biology. Support for H.N. was provided by Florida State University's Council on Research and Creativity 2004/2005 (project No. 014872).
References
- 1.White, S. H., and W. C. Wimley. 1999. Membrane protein folding and stability: physical principles. Annu. Rev. Biophys. Biomol. Struct. 28:319–365. [DOI] [PubMed] [Google Scholar]
- 2.Deisenhofer, J., O. Epp, K. Miki, R. Huber, and H. Michel. 1985. Structure of the protein subunits in the photosynthetic reaction centre of rhodopseudomonas viridis at 3 Å resolution. Nature. 318:618–624. [DOI] [PubMed] [Google Scholar]
- 3.Landolt-Marticorena, C., K. A. Williams, C. M. Deber, and R. A. F. Reithmeier. 1993. Non-random distribution of amino acids in the transmembrane segments of human type I single span membrane proteins. J. Mol. Biol. 229:602–608. [DOI] [PubMed] [Google Scholar]
- 4.Arkin, I. T., and A. T. Brunger. 1998. Statistical analysis of predicted transmembrane α-helices. Biochim. Biophys. Acta. 1429:113–128. [DOI] [PubMed] [Google Scholar]
- 5.Ulmschneider, M. B., M. S. P. Sansom, and A. Di Nola. 2005. Properties of integral membrane protein structures: derivation of an implicit membrane potential. Proteins. 59:252–265. [DOI] [PubMed] [Google Scholar]
- 6.Braun, P., and G. von Heijne. 1999. The aromatic residues Trp and Phe have different effects on the positioning of a transmembrane helix in the microsomal membrane. Biochemistry. 38:9778–9782. [DOI] [PubMed] [Google Scholar]
- 7.Whiles, J. A., K. J. Glover, R. R. Vold, and E. A. Komives. 2002. Methods for studying transmembrane peptides in bicelles: consequences of hydrophobic mismatch and peptide sequence. J. Magn. Reson. 158:149–156. [DOI] [PubMed] [Google Scholar]
- 8.Koeppe II, R. E., F. J. Sigworth, G. Szabo, D. W. Urry, and A. Wooley. 1999. Gramicidin channel controversy: the structure in a lipid environment. Nat. Struct. Biol. 6:609. [DOI] [PubMed] [Google Scholar]
- 9.Killian, J. A., I. Salemink, M. R. R. de Planque, G. Lindbloom, R. E. Koeppe II, and D. V. Greathouse. 1996. Induction of nonbilayer structures in diacylphosphatidylcholine model membranes by transmembrane α-helical peptides: importance of hydrophobic mismatch and proposed role of tryptophans. Biochemistry. 35:1037–1045. [DOI] [PubMed] [Google Scholar]
- 10.de Planque, M. R. R., E. Goormaghtigh, D. V. Greathouse, R. E. Koeppe II, J. A. W. Kruijtzer, R. M. J. Liskamp, B. de Kruijff, and J. A. Killian. 2001. Sensitivity of single membrane-spanning α-helical peptides to hydrophobic mismatch with a lipid bilayer: effects on backbone structure, orientation, and extent of membrane incorporation. Biochemistry. 40:5000–5010. [DOI] [PubMed] [Google Scholar]
- 11.de Planque, M. R. R., B. B. Bonev, J. A. A. Demmers, D. V. Greathouse, R. E. Koeppe II, F. Separovic, A. Watts, and J. A. Killian. 2003. Interfacial anchor over hydrophobic matching effects in peptide-lipid interactions. Biochemistry. 42:5341–5348. [DOI] [PubMed] [Google Scholar]
- 12.Persson, S., J. A. Killian, and G. Lindblom. 1998. Molecular ordering of interfacially localized tryptophan analogs in ester- and ether-lipid bilayers studied by 2H-NMR. Biophys. J. 75:1365–1371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Yau, W.-M., W. C. Wimley, K. Gawrisch, and S. H. White. 1998. The preference of tryptophan for membrane interfaces. Biochemistry. 37:14713–14718. [DOI] [PubMed] [Google Scholar]
- 14.Gaede, H. C., W.-M. Yau, and K. Gawrisch. 2005. Electrostatic contributions to indole-lipid interactions. J. Phys. Chem. B. 109:13014–13023. [DOI] [PubMed] [Google Scholar]
- 15.Kachel, K., E. Asuncion-Punzalan, and E. London. 1995. Anchoring of tryptophan and tyrosine analogs at the hydrocarbon-polar boundary in model membrane vesicles: parallax analysis of fluorescence quenching induced by nitroxide-labeled phospholipids. Biochemistry. 34:15475–15479. [DOI] [PubMed] [Google Scholar]
- 16.Grossfield, A., J. Sachs, and T. B. Woolf. 2000. Dipole lattice membrane model for protein calculations. Proteins. 41:211–223. [DOI] [PubMed] [Google Scholar]
- 17.Tanizaki, S., and M. Feig. 2005. A generalized born formalism for heterogeneous dielectric environments: an application to the implicit modeling of biological membranes. J. Chem. Phys. 122:124706. [DOI] [PubMed] [Google Scholar]
- 18.Grossfield, A., and T. B. Woolf. 2002. Interaction of tryptophan analogs with POPC lipid bilayers investigated by molecular dynamics calculations. Langmuir. 18:198–210. [Google Scholar]
- 19.Woolf, T. B. 1998. Molecular dynamics simulations of individual α-helices of bacteriorhodopsin in dimyristoylphosphatidylcholine. II. Interaction energy analysis. Biophys. J. 74:115–131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.MacCallum, J. L., and D. P. Tieleman. 2006. Molecular dynamics calculations of the distribution of amino acid side chains in a lipid bilayer. Biophys. J. 90:1026. (Abstr.). [Google Scholar]
- 21.Dougherty, D. A. 1996. Cation-π interactions in chemistry and biology: a new view of benzene, Phe, Tyr, and Trp. Science. 271:163–168. [DOI] [PubMed] [Google Scholar]
- 22.Ma, J. C., and D. A. Dougherty. 1997. The cation-π interaction. Chem. Rev. 97:1303–1324. [DOI] [PubMed] [Google Scholar]
- 23.Caldwell, J. W., and P. A. Kollman. 1995. Cation-π interactions: nonadditive effects are critical in their accurate representation. J. Am. Chem. Soc. 117:4177–4178. [Google Scholar]
- 24.Cubero, E., F. J. Luque, and M. Orozco. 1998. Is polarization important in cation-π interactions? Proc. Natl. Acad. Sci. USA. 95:5976–5980. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Minoux, H., and C. Chipot. 1999. Cation-π interactions in proteins: can simple models provide an accurate description? J. Am. Chem. Soc. 121:10366–10372. [Google Scholar]
- 26.Woolf, T. B., A. Grossfield, and J. G. Pearson. 1999. Indoles at interfaces: calculations of electrostatic effects with density functional and molecular dynamics methods. Int. J. Quantum. Chem. 75:197–206. [Google Scholar]
- 27.Haydon, D. A., and V. B. Meyers. 1973. Surface charge, surface dipoles, and membrane conductance. Biochim. Biophys. Acta. 307:429–443. [DOI] [PubMed] [Google Scholar]
- 28.Davis, M. E., and J. A. McCammon. 1990. Electrostatics in biomolecular structure and dynamics. Chem. Rev. 90:509–521. [Google Scholar]
- 29.Gawrisch, K., D. Ruston, J. Zimmerberg, V. A. Parsegian, R. P. Rand, and N. Fuller. 1992. Membrane dipole potentials, hydration forces, and the ordering of water at membrane surfaces. Biophys. J. 61:1213–1223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Zhou, F., and K. Schulten. 1995. Molecular dynamics study of a membrane-water interface. J. Phys. Chem. 99:2194–2207. [Google Scholar]
- 31.Im, W., S. Berneche, and B. Roux. 2001. Generalized solvent boundary potential for computer simulations. J. Chem. Phys. 114:2924–2937. [Google Scholar]
- 32.Ladokhin, A. S., and S. H. White. 2001. Protein chemistry at membrane interfaces: non-additivity of electrostatic and hydrophobic interactions. J. Mol. Biol. 309:543–552. [DOI] [PubMed] [Google Scholar]
- 33.Lin, J.-H., N. A. Baker, and J. A. McCammon. 2002. Bridging implicit and explicit solvent approaches for membrane electrostatics. Biophys. J. 83:1374–1379. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Stern, H. A., and S. E. Feller. 2003. Calculation of the dielectric permittivity profile for a nonuniform system: application to a lipid bilayer simulation. J. Chem. Phys. 118:3401–3412. [Google Scholar]
- 35.Marrink, S. J., and H. J. C. Berendsen. 1996. Permeation process of small molecules across lipid membranes studied by molecular dynamics simulations. J. Phys. Chem. 100:16729–16738. [Google Scholar]
- 36.Jacobs, R. E., and S. H. White. 1989. The nature of the hydrophobic binding of small peptides at the bilayer interface: implications for the insertion of transbilayer helices. Biochemistry. 28:3421–3437. [DOI] [PubMed] [Google Scholar]
- 37.Sitkoff, D., K. A. Sharp, and B. Honig. 1994. Accurate calculation of hydration free energies using macroscopic solvent models. J. Phys. Chem. 98:1978–1988. [Google Scholar]
- 38.Peterson, F. N. R., M. Ø. Jensen, and C. H. Nielsen. 2005. Interfacial tryptophan residues: a role for the cation-π effect? Biophys. J. 89:3985–3996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Aliste, M. P., J. L. MacCallum, and D. P. Tieleman. 2003. Molecular dynamics simulations of pentapeptides at interfaces: salt bridge and cation-π interactions. Biochemistry. 42:8976–8987. [DOI] [PubMed] [Google Scholar]
- 40.Huang, C., and J. P. Charlton. 1972. Interactions of phosphatidylcholine vesicles with 2-p-toluidinylnaphthalene-6-sulfonate. Biochemistry. 11:735–740. [DOI] [PubMed] [Google Scholar]
- 41.Seelig, J., and P. Ganz. 1991. Nonclassical hydrophobic effect in membrane binding equilibria. Biochemistry. 30:934–959. [DOI] [PubMed] [Google Scholar]
- 42.DeVido, D. R., J. G. Dorsey, H. S. Chan, and K. A. Dill. 1998. Oil/water partitioning has a different thermodynamic signature when the oil solvent chains are aligned than when they are amorphous. J. Phys. Chem. 102:7272–7279. [Google Scholar]
- 43.MacCallum, J. L., and D. P. Tieleman. 2006. Computer simulation of the distribution of hexane in a lipid bilayer: spatially resolved free energy, entropy, and enthalpy profiles. J. Am. Chem. Soc. 128:125–130. [DOI] [PubMed] [Google Scholar]
- 44.Tieleman, D. P., H. J. C. Berendsen, and M. S. P. Sansom. 1999. An alamethicin channel in a lipid bilayer: molecular dynamics simulations. Biophys. J. 76:1757–1769. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.van der Spoel, D., B. Hess, and E. Lindahl. 2004. GROMACS user manual version 3.2. www.gromacs.org. [Online].
- 46.Chandrasekhar, I., M. Kastenholz, R. D. Lins, C. Oostenbrink, L. Schuler, D. P. Tieleman, and W. F. van Gunsteren. 2003. A consistent potential energy parameter set for lipids: dipalmitoylphosphatidylcholine as a benchmark of the GROMOS96 force field. Eur. Biophys. J. 32:67–77. [DOI] [PubMed] [Google Scholar]
- 47.Chiu, S.-W., M. Clark, V. Balaji, S. Subramanian, H. L. Scott, and E. Jakobsson. 1995. Incorporation of surface tension into molecular dynamics simulation of an interface: a fluid phase lipid bilayer membrane. Biophys. J. 69:1230–1245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Schuler, L. D., X. Daura, and W. F. van Gunsteren. 2001. An improved GROMOS96 force field for aliphatic hydrocarbons in the condensed phase. J. Comp. Chem. 22:1205–1218. [Google Scholar]
- 49.Berendsen, H. J. C., J. P. M. Postma, W. F. van Gunsteren, and J. Hermans. 1981. Interaction models for water in relation to protein hydration. In Intermolecular Forces. B. Pullman, editor. D. Reidel Publishing, Dordrecht, The Netherlands. 331–342.
- 50.Hess, B., H. Bekker, H. J. C. Berendsen, and J. G. E. M. Fraaije. 1997. LINCS: a linear constraint solver for molecular simulations. J. Comput. Chem. 18:1463–1472. [Google Scholar]
- 51.York, D., T. A. Darden, and L. Pedersen. 1993. The effect of long-range electrostatic interactions in simulations of macromolecular crystals: a comparison of the Ewald and truncated list methods. J. Chem. Phys. 99:8345–8348. [Google Scholar]