What can be learnt from models of incidence rates?

Abstract

Models of breast cancer incidence have evolved from the observation by Armitage and Doll in the 1950s that the pattern of incidence by age differs for reproductive cancers from those of other major malignancies. Both two-stage and multistage models have been applied to breast cancer incidence. Consistent across modeling approaches, risk accumulation or the rate of increase in breast cancer incidence is most rapid from menarche to first birth. Models that account for the change in risk after menopause and the temporal sequence of reproductive events summarize risk efficiently and give added insights to potentially important mechanistic features. First pregnancy has an adverse impact on progesterone receptor negative tumors, while increasing parity reduces the risk of estrogen/progesterone receptor positive tumors but not estrogen/progesterone receptor negative tumors. Integrated prediction models that incorporate prediction of carrier status for highly penetrant genes and also account for lifestyle factors, mammographic density, and endogenous hormone levels remain to be efficiently implemented. Models that both inform and reflect the emerging understanding of the molecular and cell biology of carcinogenesis are still a long way off.

History of development

Two distinct classes of mathematical models have been used in cancer epidemiology. Statistical models draw on established mathematical structures (including linear and logistic regression) to evaluate relationships between risk factors and cancer incidence. Biomathematical models are derived by translating a series of hypotheses about the biological process involved in carcinogenesis into mathematical terms [1]. The best known models developed by Armitage and Doll lay the foundation for a long history of applying mathematical models to cancer incidence rates and with extension can relate epidemiological risk factors to cancer incidence to provide a structure to view the process of carcinogenesis [2]. Drawing on cancer mortality, Fisher and Hollomon [3]used stomach cancer statistics, and Nordling [4]combined all cancer sites and noted that for ages 25 to 74 years, the logarithm of the death rate increased in direct proportion to the logarithm of age. Armitage and Doll then built on this work to evaluate cancer mortality in the UK in men and women in 1950 and 1951. They noted that a gradient of 6 to 1 (i.e., 6 units increase in the logarithm of the death rate per unit increase in the logarithm of age) was more or less consistent across 17 cancer sites, and concluded that the theory that cancer is the end-result of several successive cellular changes is supported by cancers of the esophagus, stomach, colon, rectum, and pancreas in men and of the stomach, colon, rectum, and pancreas in women. Furthermore, a deficit in the mortality for breast, ovary, and cervical cancer in older age groups was noted by Armitage and Doll, who attributed this to a reduction during midlife in the rate of production of one of the later changes in the process of carcinogenesis [2]. Through this work, they set forth a multistage model of carcinogenesis long before laboratory or biological understanding.

These types of mathematical models can also summarize the impact of multiple variables that may modify the incidence rates, and so can provide a means to identify areas of research that require more study [5]. They may also allow for refinement and improve precision in risk estimation, and ultimately produce better tools for clinical risk assessment and decision-making regarding the use of chemopreventive agents [6]. Doll and Peto [7]applied this multistage cancer incidence model to lung cancer within the British Doctor's Study and observed that incidence is proportional to (dose + 6)² × (age - 22.5)^4.5, where dose equals cigarettes per day. This then was consistent with the multistage model of carcinogenesis, and generates coefficients for the components of the model that are not readily interpretable beyond a comparison of their magnitude and the power function that approximates the number of stages in the model. However, in this and similar models, incidence is proportional to the fourth to sixth power of time, suggesting four to six independent steps are necessary for development of cancer. Such extrapolations have been confirmed by the work of Vogelstein and colleagues documenting that more than four genetic alterations are necessary for development of colon cancer [8]. Mechanistic implications of this work for lung cancer included that more than one of the stages of lung carcinogenesis was strongly affected by smoking [9,10]. Extensive application of the Armitage and Doll model to radiation exposure also attests to its utility [11,12].

While the range of applications beyond breast cancer has been considerable, we now summarize the history of development of breast cancer models and review their findings and implications. We then consider future applications, including risk prediction and identification of women at elevated risk of breast cancer for whom chemoprevention strategies such as Tamoxifen or other agents may be suitable [13].

Breast cancer applications

Focusing on breast cancer, Moolgavkar and colleagues [14,15]took an alternative approach to the Armitage and Doll model, again using the age-incidence data from high and low risk countries. These authors fitted a two-stage model that had normal cells progress through transformed cells to cancer. The first stage may change the rate at which the first transition or initiation occurs. A second stage changes the net proliferation rate of initiated cells, promoting progress to cancer. They noted that across high and low risk countries the shape of the incidence curve was constant and the impact of later age at first birth was also constant. The rise in risk through the premenopausal years identified here points to the importance of accumulating risk up to menopause as a determinant of the postmenopausal incidence. Pathak and Whittemore [16]applied a breast cancer incidence rate function to data from countries with high, medium, and low breast cancer incidence rates and confirmed the observation of Moolgavkar and colleagues that age at first birth and age at menopause exert similar effects on all women regardless of breast cancer rates in their country. Subsequent work by Pike and colleagues [17]using traditional survival analysis methods in a prospective cohort showed that reproductive risk factors apply equally across ethnic groups in the US.

Pike and colleagues [18]took the Armitage and Doll approach and fitted a model that included menarche, first birth, and menopause as modifiers of the effect of time. This model assumed that breast tissue 'aged' at a constant rate, starting at menarche and continuing to first birth. The Pike model allowed for an adverse effect of first birth and a decrease in the rate of 'tissue aging' after the first birth, basing this proposed model on epidemiological data that supported these assumptions. The rate of tissue aging further decreased after menopause (Figure 1). This then was consistent with the early Armitage and Doll observation that the rate of increase in breast carcinogenesis was lower later in life [2]. This model did not account for more than one pregnancy or the timing of pregnancies after the first. The output from this model, like the Doll and Peto lung cancer model, is a set of parameters for the rate of breast tissue aging before first pregnancy, the rate of tissue aging after menopause, and the magnitude of the adverse effect of first pregnancy (Table 1). Compared to the constant rate of tissue aging from menarche to first birth, the rate of aging was 0.8 per year after first birth and 0.105 after menopause. The adverse effect of first birth was equivalent to 2.2 years of aging.

Figure 1.

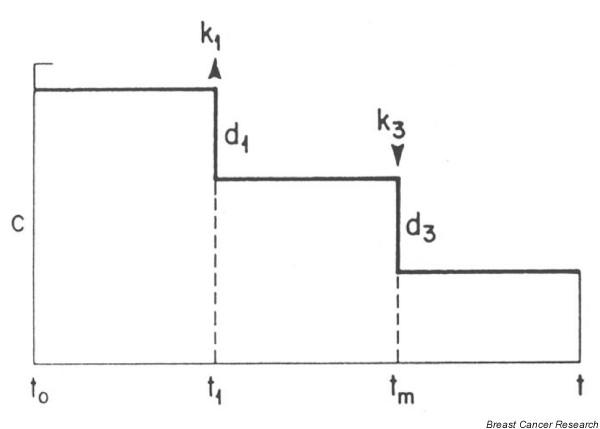
Pike model of breast cancer incidence.

Table 1.

Parameters for estimated rate of tissue aging from the Pike incidence model and Rosner extended model

		Rosner, Colditz and Willett [19]
Rate of tissue aging	Pike et al. [18]	One-birth model	Two births	Multiple births
Menarche to first birth	1.0	1.0	1.0	1.0
After first birth, before menopause	0.70	0.67 (p < 0.001)	0.84 (p = 0.19)	0.79 (p = 0.002)
After second birth			0.68 (p = 0.20)	0.03a (p = 0.02) (per year from birth to menopause, for each birth)
After menopause	0.105	0.43 (p = 0.002)	0.43 (p = 0.002)	0.46b(p = 0.002)
Increase at first birth (years)	2.2	7.45 (p < 0.001)	6.4 (p = 0.02)	7.61 (p < 0.001)
Increase at second birth			-0.02 (p = 0.99)	-1.69
K	Fixed at 4.5	2.9 (2.5–3.3)	2.8 (2.4–3.2)	2.8 (2.4–3.2)

^aFor the multiple birth model this represents the decrease in the rate of tissue aging per year with each subsequent birth after the first, so for births at 27, 30 and 33 with menopause at age 50 the cumulative rate of tissue aging is decreased by 1.11 units.^bAssumes three births. The log likelihood for multiple births model is significantly better than the one-birth model (χ², 2 df 17.82, p < 0.001).

Rosner and Colditz have expanded on this Pike model of breast cancer incidence to include additional reproductive events: subsequent births after the first, type of menopause in addition to age at menopause, and the premenarche period [19,20]. We first applied the Pike model [19](see Table 1 for parameter estimates in terms of the rate of tissue aging). Specifically, we observed that the one-birth model gave a rate of tissue aging after first birth that was 0.67, close to the Pike estimate. After menopause the rate was 0.43, substantially higher than the Pike estimate, but perhaps influenced by differences in the populations used to generate the model estimates. We observed the adverse effect of first pregnancy as equivalent to 7.45 years of tissue aging. Because this model generates parameters that are not readily interpretable in the context of relative risks and the broader epidemiological literature, we modified the time scale to a log-incidence model [20]. The log-incidence model, which explicitly attempts to develop cumulative measures of exposure over long periods of time, utilizes these cumulative measures in a relative risk context to predict breast cancer incidence. Thus output is more easily interpreted than coefficients for tissue aging from the Pike model. The basis for the model is similar to the Moolgavkar and Knudson two-stage model for cancer incidence [15]. Moolgavkar proposes one stage from normal cells to intermediate cells, and a second stage from intermediate cells to malignant cells. Since the number of intermediate cells is not observable, it isn't clear that it is possible to distinguish these two phases with actual data and we have chosen to use the number of intermediate cells as a latent variable (c(t)), which is impacted by different risk factors, possibly differentially at different ages.

The approach to model fitting by Rosner is to follow Nunney [21], who assumes that number of cell divisions and hence incidence at time t is proportional to the number of breast cell divisions accumulated up to age t, or Pikes 'breast tissue age'. The log of the rate of tissue aging is assumed to be a linear function of risk factors that are relevant at a given age. This differs slightly from the Pike model of breast tissue age, which assumes that log(incidence) is a linear function of log(time) or log(breast-tissue age). In the original Pike model of breast cancer incidence (Figure 1), tissue age increased at a constant rate c from menarche to first birth. At the time of first birth there was an immediate increase in breast tissue age (of magnitude k₁), and a corresponding decrease in the rate of breast tissue aging after first birth to a rate (c - d₁). Breast tissue age increased at the same rate from first birth to age 40 years, after which the rate of increase diminished linearly until at menopause the rate of increase was d₃units lower than at age 40 years.

The underlying assumption of this model is that cell division is proportional to t, the age of the individual, and that reproductive factors modify the rate of cell division after first birth and again after menopause, as observed in animal models where the cell cycle is longer after first birth [22]. Armitage [23]has referred to this adaptation by Pike as a 'time transformation theory', and concludes that the changes in response function are more specific than required by the two-stage model and, furthermore, that it is unclear whether this model provides an explanation for initiator, promoter, or other data relating early and late effects. It does, however, approximate known changes in risk associated with biological events and associated changing hormonal exposures of women.

Early versions of the Pike model did not include terms for the spacing of pregnancies, did not accommodate premenopausal women (who have no age at menopause), and did not easily accommodate pregnancies after age 40 years. Furthermore, the parameters of the breast tissue-aging model are difficult to interpret from a relative risk perspective. To implement this log-incidence model, we constructed a life calendar for each risk factor and applied this model to the Nurses' Health Study to evaluate risk factors and also predict risk up to a defined age, such as 70.

We noted that the first pregnancy has an adverse effect that is dependent on the interval from menarche to the age at first pregnancy, that is, the later the first pregnancy the larger its adverse effect [24]. Evaluating second and subsequent pregnancies, we noted no adverse effect for the pregnancies after the first [19]. Importantly, we also confirmed the work of Trichopoulos and colleagues [24], who suggested that the timing of births was important; the closer births are together the lower the risk of breast cancer. We developed a single term to summarize the timing of births across the premenopausal years, which we call the birth index. The rationale for the birth index is the assumption that at any age t, the latent variable c(t) is a linear function of parity at time t. The resulting expression for the birth index at age t for a parous woman is:

where t* = min (age, age at menopause); s = parity; t_i = age at i^th birth; i = 1,..,s; b_it = 1 if parity ≥i at age t, or = 0 otherwise. For nulliparous woman, the birth index = 0.

The net effect of pregnancy is a short-term increase in incidence then a subsequent long-term decrease. The magnitude of such changes in incidence for parous women is primarily a function of age at first birth and, to a lesser extent, ages at subsequent births, and accounts for the cross-over in incidence between parous and nulliparous women that has been reported [25].

Menopause has been recognized as a breast cancer risk modifier for many years. Detailed evaluations have shown that age at menopause is a major modifier of breast cancer risk in the postmenopausal years [26,27]. In both the Collaborative Group on Hormonal Factors in Breast Cancer reanalysis and National Health Service (NHS) data, risk of breast cancer increases by approximately 2.8% for each additional year of delay in natural menopause [28]. Bilateral oophorectomy reduces risk compared to natural menopause. Reflecting modern surgical practice, a substantial proportion of women report hysterectomy without bilateral oophorectomy. Accordingly, this leads to uncertainty as to age at menopause and raises concern for estimation of risk after menopause. Pike has argued that misspecification of age at menopause will lead to error in estimation of the effect of postmenopausal hormone therapy on breast cancer risk [29]. Adding women with uncertain age at menopause will bias results and reduce standard errors. This was exemplified in the Collaborative reanalysis of hormones and breast cancer, where the relationship between age at menopause and risk of breast cancer was attenuated when women with hysterectomy were included in the analysis. At the same time, the relationship between duration of use of postmenopausal hormones and risk was also attenuated when age at menopause was less rigorously controlled [28]. Rockhill and colleagues [30]evaluated this hypothesis using data from the NHS and showed that bias consistently underestimated the magnitude of postmenopausal hormones on breast cancer risk. Accordingly, we continue to fit the log-incidence model only to women with known age at menopause. While one could impute an age at menopause based on age, smoking, parity, and age at hysterectomy, we have shown that this too leads to biased estimates for postmenopausal hormone therapy. Current use of postmenopausal hormones carries increased risk of breast cancer; estrogen alone increases risk by 3% per year of use while estrogen plus progestin increases risk by approximately 7% per year of use.

We have also added established epidemiological risk factors, including family history, history of benign breast disease, alcohol intake, and adiposity [31]. Benign breast disease (BBD) varied the impact of age at menarche. For nulliparous BBD negative women, there was a strong effect of age at menarche; there was virtually no effect among BBD positive women. In addition, there was an increase in risk at birth for BBD positive versus BBD negative women when all other factors were held constant, possibly implying a differential genetic profile at birth. Other aspects of the reproductive profile were similar for BBD positive and negative women.

Pike and colleagues compared the initial log/log model with the two-stage model of Moolgavkar and colleagues and concluded that the multistage model, assuming all transitions are equally determined by the rate of cell turnover, "provides an excellent quantitative description of much of the known epidemiology of breast cancer" [18]. Armitage notes that the time transformed model of Pike and colleagues is less flexible than the two-stage approach, which offers greater flexibility in evaluating the time at which each factor influences risk [23]. He concludes that, "until we have clear evidence for more than two stages, it seems best to regard the multistage theory, like the dogmas of certain religions, as permitting either a literal or figurative interpretation." While modeling approaches may vary, the underlying biology and age-incidence consistently indicate that the rate of aging is most rapid from menarche to first full term pregnancy, an interval that has increased from just a few years to an average of 12 to 18 years in countries with established market economies [32]. This social evolution drives up breast cancer incidence yet the underlying biology and epidemiological data remain sparse to identify risk factors such as diet and physical activity that may attenuate the rate of risk accumulation or the magnitude of the adverse effect of delayed first pregnancy.

While screening mammography increases the detection of breast cancer, and modifies mortality after diagnosis [33], it does not change the underlying biological relationships or associations between reproductive events and risk of breast cancer. The models described above relate to the underlying incidence of cancer and appear to be consistent in their fit to incidence rates across countries that have instituted routine screening. We next consider the performance for specific subtypes of breast cancer defined by receptor status as we have previously shown that risk factors differ according to receptor status [34].

Receptor status

Incidence rates and risk factors for breast cancer differ according to both estrogen receptor (ER) and progesterone receptor (PR) status. Furthermore, therapeutic approaches to treatment and chemoprevention differ for tumors based on receptor status. Thus, it would be prudent to divide breast cancer according to the status of both of these tumor receptors to better understand the etiology of each subtype and then to more accurately estimate risk.

Initial studies of risk factors for ER status among breast cancer cases have typically considered age [35,36]or age and risk factors one at a time [37-48]. Many of these studies had not classified cases jointly by both ER and PR status, in large part due to small sample size. Few risk factors show any consistent difference between ER positive (ER+) and ER negative (ER-) breast cancer, although parity is somewhat more inversely related to ER+ tumors in some studies [42-44,46], but not in others [41]. To apply an integrated approach, we fitted the Rosner and Colditz model of breast cancer incidence to cases classified jointly according to ER and PR status [34]. We observed significant heterogeneity among the four breast tumor categories for age, menopausal status, body mass index (BMI) after menopause, the one-time adverse effect of first pregnancy, and past use of postmenopausal hormones but not benign breast disease, family history of breast cancer, alcohol use, and height. The one-time adverse effect of first pregnancy is present for PR-but not PR+ tumors after controlling for ER status (p = 0.007). An opposite result is observed for BMI after menopause, it being strongly related to PR+ but not PR-tumors after controlling for ER status (p = 0.005). Significant differences were observed for ER status for age (p = 0.003) and past use of postmenopausal hormones (p = 0.01).

Models predicting genetic susceptibility

Genetic susceptibility and prediction of carrier status

For subgroups of the population that may carry genetic susceptibility to certain cancers [49], preventive interventions may differ from the broader population. For example, several early studies indicated that breast cancer tended to aggregate in families [50,51]. Compelling evidence for a genetic component to breast cancer came from the Cancer and Steroid Hormone (CASH) study. Initial analyses confirmed that cases were significantly more likely than controls to have a family history of the disease, especially the earlier the age at onset of the case [52]. A segregation analysis of the pattern of breast cancer in the case families provided evidence that the susceptibility was transmitted in a Mendelian manner [53]. Linkage analysis using DNA markers generated in the laboratory localized the first putative gene to a region of chromosome 17q21 [54], and BRCA1 was subsequently identified through positional cloning [55].

Parmigiani and colleagues [56]developed a Bayesian model to evaluate the probabilities that a woman is a carrier of a mutation of BRCA1 and BRCA2 using breast and ovarian cancer history of first and second degree relatives as predictors. Efforts to combine both lifestyle factors and genetic carrier prediction have been limited, in part by the divergent mathematical underpinnings of the approaches in the two areas. One approach from the UK has been published [57]. In that model, Tyrer and colleagues incorporated BRCA1, BRCA2, and a hypothetical low penetrance gene, as well as some personal risk factors (including age at menarche, age at first birth, height, BMI, and age at menopause). The model omitted established risk factors, including type of menopause and use of post-menopausal hormones, and maintained a fixed adverse effect of age at first birth of 30 years or older. The model combined estimates from various epidemiological studies and calibrated predicted incidence against UK national statistics.

Risk prediction

Breast cancer incidence models have also been applied to predict individual probabilities of carrier status for specific mutations that drive risk of breast cancer and, alternatively, based on a varying number of risk factors, to predict the risk of breast cancer over a defined time period, say 5 or 10 years. The larger the number of risk factors considered, the higher the likelihood the prediction model will separate those at risk of disease from those who are not as likely to develop disease. However, as Wald and colleagues [58]note, to be useful as a screening test or an individual marker of risk or to identify those who will develop disease and those who will not, the magnitude of association for a predictor must be in the order of 10 or higher comparing extreme quintiles for a detection rate of 20%. No prediction models for breast cancer have achieved this level of discrimination to date.

Ottman and colleagues [59]published a simple model in 1983 that calculates a probability of breast cancer diagnosis for mothers and sisters of breast cancer patients. They used life-table analysis to estimate the cumulative risks to various ages based upon two groups of patients from the Los Angeles County Cancer Surveillance Program, then derived a probability within each decade between ages 20 and 70 for mothers and sisters of the patients, according to the age of diagnosis of the patient and whether the disease was bilateral or unilateral.

Because risk factors may change over the life course (weight gain, change in alcohol intake, menopausal status, use of postmenopausal hormones for some years, and so on) it becomes more helpful to consider the impact of all these risk factors on breast cancer cumulative risk up to a given age, say 70 or 75. This approach has been developed for breast cancer risk according to family history [60], and the prediction of BRCA1 carrier status [56,61], but more general applications joining carrier status and lifestyle factors remain limited [57].

The complex nature of breast cancer incidence, with many possibly time-dependent risk factors, requires prediction models that account for this variation over time. These are now shown to outperform traditional approaches that fit indicator variables with fixed effects across time [62]. In addition, the log-incidence model of Rosner and Colditz performs significantly better than the commonly used Gail model for total breast cancer incidence, which includes only five variables (age, age at menarche, age at first birth, number of benign breast biopsies, and family history).

The efficacy of chemoprevention for breast cancer is clearly shown for ER+ disease, reducing risk by 50% [13]. Given the need to balance risks and benefits when implementing a Tamoxifen-based chemoprevention strategy [63], a model that successfully identifies women at increased risk of ER+ breast cancer will, therefore, improve the risk benefit ratio. Colditz and Rosner have applied their log-incidence model to breast cancers classified according to receptor status and reported that the area under the receiver operator characteristic curve adjusted for age was 0.630 (95% confidence interval = 0.616 to 0.644) for ER+/PR+ tumors and was 0.601 (95% confidence interval = 0.575 to 0.626) for ER-/PR- tumors, indicating adequate discriminatory accuracy (unpublished data). On the other hand, when we fitted the Gail model to the same data set it had performance characteristics that were somewhat lower than the Rosner and Colditz model, with values of 0.578 for total cancer and 0.57 for ER+PR+ tumors. The difference between the area under the ROC curve for the Rosner and Colditz model versus the Gail model for total breast cancer was statistically significant (p < 0.0001), indicating that the more complete modeling of risk factors across the life course could be more useful for discriminating among those women at high and low risk of breast cancer.

Growing efforts are in place to add endogenous hormone levels and mammographic density to models that rely on established epidemiological risk factors. To date, addition of mammographic density has added little to the performance of models as simple as the Gail model, increasing the area under the ROC curve by just 1% [64]. Endogenous hormone levels have not yet been added to prediction models.

Conclusions and future directions

We have summarized the evolution of models applied to breast cancer incidence data. These models show that biologically meaningful applications can help reduce bias in estimates of risk factors for breast cancer, and may be used to improve risk prediction. Easy to interpret applications that combine risk prediction for high penetrance genes along with lifestyle factors remain to be implemented. Meanwhile, those that accommodate lifestyle factors alone are available as web tools for use in clinical practice and more generally to guide women in their understanding of risk factors and lifestyle choices that may reduce their risk.

Insights from models may foster additional research. Examples include the finding for benign breast disease, suggesting that early life events may be important [65]. Yet to date limited epidemiological data are available to explore this hypothesis, although one study suggests that diet may dramatically influence the risk of proliferative benign lesions [66]. We can look forward eventually to models that both inform and reflect the emerging understanding of the molecular and cell biology of carcinogenesis, but that is still a long way off.

Abbreviations

BBD = benign breast disease; BMI = body mass index; ER = estrogen receptor; PR = progesterone receptor.

Competing interests

The authors declare that they have no competing interests.