Pharmacokinetic-Pharmacodynamic Modeling of the Electroencephalogram Effect of Norfloxacin in Rats

Abstract

A previously developed pharmacokinetic-pharmacodynamic (PK-PD) modeling approach was used to investigate the epileptogenic activity of norfloxacin as a representative antibiotic with concentration-dependent antimicrobial activity. Rats received an intravenous infusion of norfloxacin at a rate of 5 mg kg of body weight⁻¹ min⁻¹ over 30 min. Blood samples were collected for drug assay, and an electroencephalogram (EEG) was recorded during infusion and postinfusion. An important delay was observed between concentrations of norfloxacin in plasma and the EEG effect. Indirect effect models failed to describe these data, which were successfully fitted by using an effect compartment model with a spline function to describe the relationship between effect and concentration at the effect site, as previously observed with imipenem. The robustness of the PK-PD model was then assessed by keeping the dose constant but increasing the duration of infusion to 120 and 240 min. Although this was accompanied by PK modifications, PD parameters did not vary significantly, and the PK-PD model still applied. In conclusion, the successful PK-PD modeling of the norfloxacin EEG effect in rats should be considered to predict and reduce the epileptogenic risk associated with this antibiotic as a representative fluoroquinolone (E. Fuseau and L. B. Sheiner, Clin. Pharmacol. Ther. 35:733-741, 1984).

Some anti-infectious compounds, including fluoroquinolones and carbapenem antibiotics, may induce central nervous system (CNS) side effects that vary in both intensity and frequency (3, 18). We have recently developed an experimental approach using quantitative electroencephalogram (EEG) recording together with pharmacokinetic-pharmacodynamic (PK-PD) modeling to characterize the epileptogenic activity of imipenem in rats (9). This investigation led to the conclusion that there was no simple direct relationship between the antibiotic's concentration in plasma and its EEG effect. However, for the same dose administered, the intensity of this undesirable effect could be dramatically reduced by decreasing the infusion rate and thereby increasing its duration. Dose fractionation should therefore limit the epileptogenic risk. Fluoroquinolones belong to another category of antibiotics with potential convulsant risk (3, 18). Our group has extensively investigated the convulsant activity of norfloxacin (NOR) by crude PK-PD approaches in laboratory animals (6-8). The purpose of the present work is to characterize NOR's epileptogenic activity as a representative fluoroquinolone by quantitative EEG recording and PK-PD modeling in rats.

MATERIALS AND METHODS

Chemicals.

NOR was obtained from Sigma (Saint-Quentin Fallavier, France). A NOR salt was prepared as previously described (7). All chemicals used were of analytical grade, and analytical solvents were of high-performance liquid chromatography grade.

Animals.

Male Sprague-Dawley rats from Depres Breeding Laboratories (St. Doulchard, France), weighing 292 ± 34 g, were used. The animals were placed in wire cages on a 12-h light-dark cycle for minimum of 8 days before the beginning of experiment, to adjust to the new environment and to overcome stress possibly incurred during transit. During this period, they had free access to food (Extralabo M20; UAR Laboratories, Villemoisson-sur-Orge, France) and water. Ethical approval was obtained from the Animal Ethics Committee of the Faculty of Pharmacy (BHE/2001/12/AE).

Surgical procedure. (i)

Implantation of cortical electrodes for the EEG recording. Five days before experiment, each rat was anesthetized with isoflurane (Forene; Abbot) inhalation. The rat was placed in a hermetic enclosure, which was supplied with an air-isoflurane mixture (3.7%) at a flow rate of 500 ml min⁻¹ (Anaesthesia Unity; Univentor 400 [Phymep, Paris, France] and air pump [Pumps Ltd., Charles Austen, Surrey, United Kingdom). When the animal was sleeping, a mask was placed on his muzzle, and the concentration of isoflurane was decreased to 1.7% for the rest of surgery. The anesthetized rat was placed on the stereotaxic instrument (David Kopf Instruments, Tujunga, Calif.) and then connected to a CMA 150 temperature controller (homeothermic blanket control unit; Phymep). A midline incision was made to expose the skull, and four electrodes were screwed into little holes drilled into the skull at the following positions in relation to the bregma: 2 mm anterior, 2 mm lateral (F1 and F2); 5 mm posterior, 2 mm right lateral (O2); and 6 mm anterior, 2 mm lateral (reference electrode). The stainless steel electrodes were connected to a miniature plug (Electro Din 5 pins, ref. MDF5B; OHM Electronique, Poitiers, France), which was fixed to the skull with two types of dental cement. The first type, a cement with aqueous solvent (Aquacem; Densply Detrey, Konstanz, Germany), was used directly in contact with the skull, and the second, a second cement with organic solvent (Swebond Rapid; Svedia Dental Industri, Enkoping, Sweden), was used to finalize the mounting. The animal was placed in a thermostatted chamber (27°C) and was allowed to recover for 4 days before catheter implantation.

(ii) Implantation of blood femoral catheters.

The day before the experiment, rats were anaesthetized by isoflurane inhalation as previously described. The polyethylene catheters inserted corresponded to the connection of two catheters with different diameters: the first, which had a small diameter (inside diameter, 0.26 mm; outside diameter, 0.61 mm; Phymep), was connected to a larger catheter (inside diameter, 0.58 mm; outside diameter, 0.96 mm; Harvard Apparatus, Les Ulis, France). Two catheters filled with 0.9% NaCl were implanted: one in the left femoral vein for drug administration and the other in the left femoral artery for blood sample collection. Animals were housed individually in plastic cages. They had free access to food and water.

Drug administration.

NOR was injected intravenously at a dose of 150 mg kg of body weight⁻¹ (422 μM kg⁻¹). The NOR solution was prepared by dissolving an adequate quantity of NOR salt in 0.9% NaCl so that the final volume of administration was set at 1 ml. The day of the experiment, the awake rats in group I received an intravenous infusion of NOR at 5 mg kg⁻¹ min⁻¹ over 30 min, corresponding to a dose equal to 150 mg kg⁻¹ (group I: n = 8, weight = 292 ± 43 g). Rats of groups II and III received the same dose of NOR, either as an infusion rate of 1.25 mg kg⁻¹ min⁻¹ over 120 min (group II: n = 6, weight = 303 ± 11 g) or at an infusion rate of 0.625 mg kg⁻¹ min⁻¹ over 240 min (group III: n = 8, weight = 282 ± 35 g). Drug infusions were started between 8:30 and 9:00 a.m. Arterial blood samples (200 to 250 μl) were collected in heparinized vials at 5, 15, 30, 60, 180, 300, 420, and 540 min for group I; 30, 90, 120, 150, 180, 300, 420, and 540 min for group II; or 30, 60, 180, 240, 270, 300, 420, 540, and 660 min for group III after the start of infusion. Immediately after collection, blood samples were centrifuged at 11,000 × g for 10 min at 4°C, and plasma was harvested and frozen at −20°C until analysis. Blood was replaced with an equal volume of 0.9% NaCl solution.

EEG measurement.

On the day of the experiment, each rat was maintained in a plastic bowl, and the miniature plug was connected to a moving connector to record the EEG signal. Bipolar EEG leads (F1-F2 and F2-O2) were continuously recorded with both Bio-Logic software and a paper polygraph (System 50,000 EEG recorder; Van Gogh, Medelec, Paris, France). The signal was band-pass filtered from 0.3 to 70 Hz. The EEG signal from the frontal cortical lead (F1-F2) was simultaneously sampled at 128 Hz and analyzed online by fast Fourier transform (FFT) to determine the EEG total power (14) in the frequency band from 0.5 to 30 Hz (Data Wave Technologies). The FFTs were calculated every 2 s, giving a first EEG power trend that could be visualized before being stored on the hard disk. Subsequently, after artifact removal from this power trend, a data reduction was calculated by averaging the first FFT trend every 5 min, resulting in a second trend. Consequently, each data point of the second trend was the mean of 150 consecutive points of the first trend. Corresponding data points of the second trend were used as effect measures for PK-PD modeling. The EEG recordings started 20 min before NOR intravenous infusion and continued until the signals had returned to their baseline values. The EEG recording duration lasted for about 9 h for groups I and II and 11 h for group III.

Plasma sample analysis.

The chromatographic system used to analyze NOR in plasma samples consisted of a Shimadzu LC-6A pump and a Waters 710A Autosampler connected to a fluorescence detector (Waters 470). Data were recorded and processed with a Waters 746 integrator. The flow rate was 0.8 ml min⁻¹, and the mobile phase consisted of 0.1 M aqueous citric acid solution containing 8% (vol/vol) acetonitrile and 10 mmol of tetra butyl ammonium perchlorate liter⁻¹. The excitation and emission wavelengths were 280 and 445 nm, respectively. The retention time of NOR was equal to 3.8 min.

Proteins from plasma samples (50 μl) were precipitated by the addition of 200 μl of perchloric acid (1 N). The mixture was then centrifuged (10,000 rpm for 5 min), and 20 μl of the supernatant was injected onto a Kromasil C₁₈ column (5-μm-diameter particles, 150 by 3 mm inner diameter; Varian, Paris, France). Initial plasma samples collected in rats of group I at 5, 15, and 30 min were diluted with blank rat plasma (1/2 [vol/vol] for 5- and 15-min sampling times and 1/3 [vol/vol] for the 30-min sampling time). The within-day variability of the method was characterized at two concentrations: 100 and 1.56 μM, with coefficients of variation (n = 6) equal to 8.8 and 4.5%, respectively, and with accuracies (n = 6) equal to 100.4 and 103.1%, respectively. The between-day variability of the method was characterized each day of the analysis at two different concentrations: 50 and 3.125 μM with coefficients of variation equal to 6.8 and 7.0%, respectively (n = 12), and with accuracies equal to 97.3 and 99.5%, respectively (n = 12).

Noncompartmental PK analysis.

Plasma NOR PK parameters were determined in each individual rat by a noncompartmental approach according to standard procedures and with the software WinNonLin (version 1.1; SCI Software, Cary, N.C.). The elimination rate constant (k_el) and it's corresponding half-life (t_{1/2 z plasma}) were estimated by ordinary least-square fit of data points (time, log plasma drug concentration) in the terminal phase of the decline and expressed, respectively, per minute and in minutes. The area under the plasma drug concentration-time curve between zero and the last point of the curve (AUC_0→tlast) was calculated by the linear trapezoidal method. The area remaining under the curve after the last measured concentration (AUC_extrapolated) was determined from C(t_last)/k_el where C(t_last) is the last measured concentration. The total area under the plasma concentration-time curve from zero to infinity (AUC) was obtained by adding AUC _extrapolated to AUC_0→tlast and expressed as the micromolar concentration in minute. Total body clearance (CL) was calculated as CL = dose/AUC and expressed in milliliters per min per kilogram. The steady-state volume of distribution (V_ss), expressed in milliliters per kilogram, was obtained from (dose × AUMC)/(AUC)², where AUMC is the total area under the moment curve (i.e., the curve of the product of concentration and time versus time from zero to infinity). The AUMC was calculated by the linear trapezoidal method. PK linearity was tested by comparing the AUC, CL, and V_ss between groups.

Modeling procedures. (i) PK modeling.

A two-compartment open model was used to characterize the plasma drug concentration (C_P)-time profiles of NOR during and after intravenous infusion:

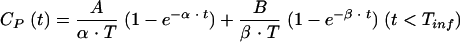(1)

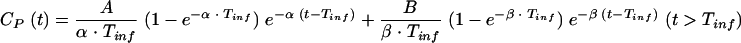(2)

where C_P(t) is the concentration of NOR in plasma at time t, A and B are the intercept values expressed in micromolar concentration, α and β are the exponential coefficients expressed per minute, and T_inf is the duration of infusion expressed in minutes.

The selected model was the model offering the best mix among good-fit, low-variation coefficients for each estimated parameter, a random repartition of weighted residues, and best values according to the criteria of Akaïke and Schwarz (1, 15).

(ii) PK-PD modeling.

Previous estimates of PK parameters were fixed, and the PD models were regressed to the EEG data for each rat by using the nonlinear least-squares program WinNonLin. An effect compartment model (16) with uniform weights was applied to analyze the PK-PD relationship by using the following equations for minimization of the hysteresis observed in the plasma drug concentration-EEG effect relationship:

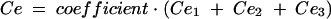(3)

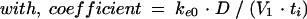(4)

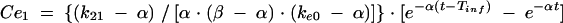(5)

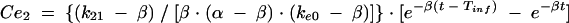(6)

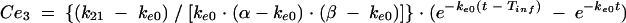(7)

In these equations, Ce is the drug concentration in the effect compartment at time t, and k_e0 is the rate constant for elimination of the drug from the effect compartment. The other parameters are the PK parameters previously defined and used as constants for PK-PD modeling (V₁ is the central compartment volume, and k₂₁ is the transfer microconstant between compartments 2 and 1).

The profile of the EEG effect was described with a spline function derived from the Hill equation (5):

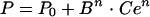(8)

In this equation, P is the total power (EEG effect) expressed in square millivolts and corresponding to Ce, P₀ is the baseline effect value estimated by averaging the 20th min of the EEG record and expressed in square millivolts, Bⁿ is the combined parameter E_max/EC₅₀ⁿ (EC₅₀ is the 50% effective concentration) expressed in square millivolts per micromolar concentration, and n is a sigmoïdicity factor determining the steepness of the curve. Goodness-of-fit was individually assessed by visual inspection and residues analysis and from the coefficients of variation associated with parameter estimates. The robustness of the compartment effect model was assessed by comparing PK-PD parameter estimates (B, n, and k_e0) between groups I, II, and III. The maximum intensity of the EEG signal (P_max), the corresponding time of occurrence (TP_max), and the period of time elapsed between the end of infusion and the effect peak (ΔT) observed after infusion of 150 mg of NOR kg⁻¹ over 120 min (group II) or over 240 min (group III) were compared to the corresponding values obtained by simulations with individual parameters estimated in rats receiving 150 mg of NOR kg⁻¹ over 30 min (group I), which for this purpose were assumed to be constant, independently of the dosing regimen.

Basic indirect models were tested, although without success (13).

Statistics.

All PK and PK-PD parameters estimates are reported as means ± standard deviations. Paired Student's t tests were used to compare the values of the PK parameters between the compartmental and noncompartmental approaches. For between-group comparisons of PK and PK-PD parameters, parametric one-way analysis of variance was used after applying Bartlett's test to check for homogeneity of variances (17). Nonparametric Kruskal-Wallis tests were used when variances were not found to be homogenous (20). Unpaired Student's t tests were used to compare the simulated and fitted values of the derived parameters (P_max, TP_max, and ΔT) within groups. A significance level of 5% was selected. Statistical comparisons were conducted with the Graph Pad PRISM software, version 2.01 (24 June 1996; Graph Pad Software, Inc., San Diego, Calif.).

RESULTS

Decay of plasma NOR concentrations with time was biexponential independently of the duration of infusion. No statistical difference was observed between mean values of PK parameters estimated by compartmental and noncompartmental approaches (Table 1). Statistically significant differences were observed between mean values of C_max, as well as the AUC, CL, and V_ss estimated in each group. CL and V_ss increased with the duration of infusion: that is, when C_max decreased. Interestingly, the effects on distribution and elimination had a tendency to compensate for each other, so that t_1/2 was independent of the experimental conditions.

TABLE 1.

PK parameter estimates obtained after intravenous infusion of 150 mg of NOR kg⁻¹ in each group of rats by noncompartmental and compartmental approaches^a

Group (n)	Infusion duration (min)	Infusion rate (mg kg−1 min−1)	Approach	Cmaxb (μM)	AUCb (μM • min)	CLb (ml min−1 kg−1)	Vssb (ml kg−1)	t1/2β (min)
I (8)	30	5	NC	188 ± 45	29,530 ± 6,495	14.9 ± 4.3	3,488 ± 757	200 ± 31
			C	211 ± 68	28,350 ± 6,686	15.6 ± 4.6	3,444 ± 755	175 ± 22
II (6)	120	1.25	NC	102 ± 15	27,860 ± 5,543	15.7 ± 3.0	3,667 ± 668	195 ± 32
			C	104 ± 12	27,870 ± 5,458	15.8 ± 3.0	3,800 ± 779	204 ± 37
III (8)	240	0.625	NC	56 ± 15	20,640 ± 4,752	21.4 ± 4.7	5,075 ± 1,269	192 ± 24
			C	57 ± 12	21,040 ± 4,698	20.7 ± 4.4	5,088 ± 1,443	210 ± 44

^aPK parameter values are means ± standard deviations.

^bNon-statistically significant differences between mean values were determined according to the approach used—compartmental (C) of noncompartmental (NC)—based on the paired Student t test. Statistically significant differences between groups are based on a one-way analysis of variance.

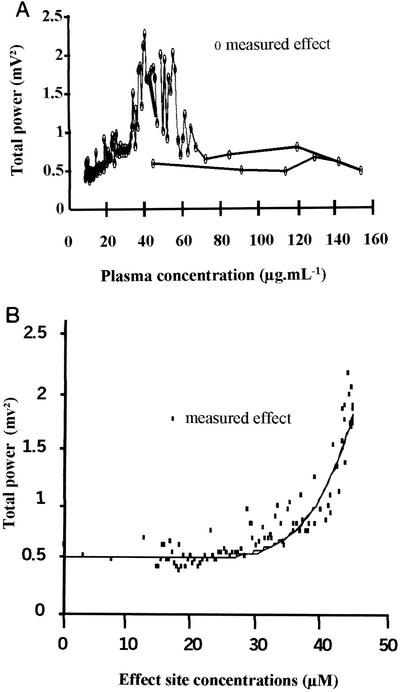
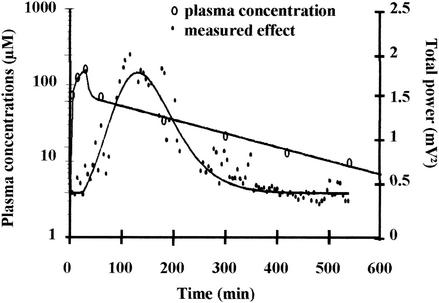
In group I, a dramatic temporal delay between plasma drug concentrations and EEG effect-time curves was observed in each rat. Only isolated spikes were observed during NOR infusion with limited effect on the total power of the EEG signal. Then the frequency and amplitude of the spikes increased dramatically, leading to a sharp increase in the total power. This was accompanied by behavioral troubles, including tremors and partial seizures. The maximum value of the total power occurred between 70 and 150 min postinfusion, depending on the animal. Then the total power came back progressively to baseline. The four basic indirect effect models (13) were tentatively fitted to these experimental data without success. In particular, they failed to describe the lag time before the total power sharply increased. Much better results were obtained with the effect compartment model (16). Individual plots of the EEG effect versus plasma NOR concentrations show a spectacular counterclockwise hysteresis (Fig. 1A). Estimations of k_e0 values permitted to collapse the hysteresis and the plot of the effect versus concentration in the effect compartment were adequately fitted with a spline function (Fig. 1B). Overall, the effect compartment model provided a good fitting of the relationship between plasma NOR concentrations and EEG effect with time as illustrated in Fig. 2. Similar observations were made with rats receiving the same dose of NOR at a longer duration of infusion (groups II and III). Although the k_e0 estimate became less precise (standard deviation much higher) as the duration of infusion increased, PK-PD parameters did not differ significantly with the duration of infusion, attesting for the robustness of the compartmental effect model in these various experimental settings (Table 2). The maximum value of the EEG effect (P_max) was reduced as the duration of infusion increased in particular from 120 min to 240 min (Table 3), in agreement with the model predictions. However, the observed P_max values were always smaller than the corresponding predicted values. Finally the time of maximum effect increased with the duration of infusion, but the delay between the effect and concentration peaks decreased (Table 3).

FIG. 1.

(A) Total power of the EEG signal versus NOR concentrations in plasma in a representative rat. (B) Total power of the EEG signal versus NOR concentrations at the effect site for a representative rat. The solid line represents the best fit of the data according to the spline function model (equation 9).

FIG. 2.

Concentrations of NOR in plasma and EEG effect versus time for the same rat as in Fig. 1. Solid lines represent best PK and PK-PD fits. The parameter values of the PK model are as follows: V = 6240 ml kg⁻¹, k₁₀ = 0.032 min⁻¹, k₁₂ = 0.168 min⁻¹, and k₂₁ = 0.028 min⁻¹. The parameter values of the PK-PD model are as follows: P₀ = 0.496 mV², B = 0.023 mV² μM⁻¹, n = 7.4, and k_e0 = 0.009 min⁻¹.

TABLE 2.

PK-PD parameter estimates obtained after an intravenous infusion of 150 mg of NOR kg⁻¹ in rats by the link model approach and the spline function model^a

Group (n)	Infusion rate (mg kg−1 min−1)	Infusion duration (min)	P0 (mV2)b	B (mV2 μM−1)c	nc	ke0 (min−1)b
Group I (8)	5	30	0.497 ± 0.222	0.017 ± 0.006	3.2 ± 2.0	0.009 ± 0.003
Group II (6)	1.25	120	0.744 ± 0.756	0.020 ± 0.005	3.0 ± 2.3	0.011 ± 0.009
Group III (8)	0.625	240	0.401 ± 0.198	0.014 ± 0.010	1.9 ± 1.3	0.029 ± 0.045

^aPK-PD parameter values are means ± standard deviations.

^bNon-statistically significant difference between groups were determined based on a nonparametric Kruskall-Wallis test.

^cNon-statistically significant differences between groups were determined based on one-way analysis of variance.

TABLE 3.

Comparisons between simulated parameters characteristic of the EEG effect derived from PK-PD effect compartment model modeling conducted in rats from group I and fitted parameters in rats from groups II and III^a

Group (n)	Infusion duration (min)	Pmax (mV2)		ΔT (min)
		Simulated	Fitted	Simulated	Fitted
I (8)	30		1.642 ± 1.204		112 ± 21
II (6)	120	1.510 ± 1.090b	1.324 ± 0.782b	75 ± 21c	91 ± 96c
III (8)	240	1.260 ± 0.990c	0.589 ± 0.362c	38 ± 16c	39 ± 50c

^aParameter values are means ± standard deviations.

^bNon-statistically significant differences between simulated and fitted values within group were determined based on the unpaired Student t test.

^cNon-statistically significant differences between simulated and fitted values within group were determined based on the unpaired Student t test with Welch correction.

DISCUSSION

Quantitative EEG recording constitutes an interesting experimental approach offering a sensitive, objective, and continuous measure of the neurotoxic effects of antibiotics in rats (9). Furthermore, since variations in the total power of the EEG signal were related to behavioral modifications, occurrence of tremor, and partial seizures, these can be considered as an appropriate surrogate PD endpoint for the investigation of the epileptogenic activity of antibiotics in rats.

Simultaneous PK-PD modeling is currently considered the preferred method of analysis. No major differences were observed between the values of the PK-PD parameters estimated by simultaneous and semiparametric modeling. However, coefficients of variation were always less important in the latter case, and for that reason, the semiparametric method was used for PK-PD modeling. PK parameters estimated by the compartmental approach were used for PK-PD modeling. No statistical differences were observed between PK parameters estimated by compartmental and noncompartmental approaches.

Interestingly PK-PD modeling of the NOR EEG effect compares favorably with what was previously obtained with imipenem (9). In particular the compartment effect model, but not the indirect effect model, applied to both drugs. CNS diffusion of these two antibiotics is limited and presumably slow (7, 10), which could explain the time delay between the peak of effect and the peak of concentration. However, when the rate of influx to the brain is very low, the efflux due to the cerebrospinal fluid bulk flow and/or for some compounds the presence of active efflux transport systems may be greater than the influx, which is in turn responsible for an early and low concentration peak in brain (12). Therefore a slow CNS distribution is not necessarily responsible for a delayed concentration-time curve in brain compared to that in plasma, nor for a delayed effect. Observed delay in the central effects of drugs with slow diffusion has been attributed to this PK characteristic in the case of morphine-6-glucuronide (2), but to a PD process with gabapentin (19).

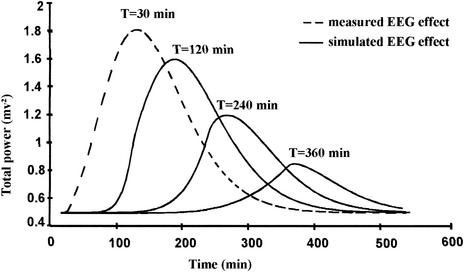
However, subtle differences exist between NOR and imipenem. In particular, the Hill coefficient value was smaller on average, and accordingly the occurrence of generalized seizures was less sudden with NOR. This is probably the reason why the range of active but nonlethal doses (i.e., doses just enough to produce a significant but reversible EEG effect) was larger with NOR than with imipenem. Yet, the robustness of the PK-PD model could not be assessed by changing the dose, since preliminary experiments showed that no EEG effect was observed when the dose was reduced by 50%, and animals died before the end of the experiment when the dose was increased by 50%. The model robustness was therefore tested by keeping the dose constant but changing the infusion duration, as previously done with imipenem (9). The compartment effect model predicts that the peak of effect should decrease as the infusion duration increases, which was confirmed experimentally (Table 3 and Fig. 3). As already shown with imipenem, the k_e0 estimate was less precise as the duration of infusion increased (9). This is probably due to the fact that k_e0 reflects a disequilibrium between drug concentration in the systemic circulation and in the biophase, which tends to disappear as infusion duration increases. Finally comparisons between simulated and observed P_max values were complicated by the fact that NOR PK parameters, which were kept constant for simulation purposes, actually varied with the duration of infusion (Table 1). Although difficult to explain, this nonlinear PK of NOR in rats is consistent with previously published data (4). The observed P_max values after long durations of infusion were smaller than the predicted values, consistent with the fact that under these circumstances, clearance increased and therefore drug exposure (AUC) decreased.

FIG. 3.

Simulated EEG effect following NOR infusions at a dose of 150 mg kg⁻¹ for various durations (same rat and parameter values as in Fig. 1 and 2).

In conclusion, for a given dose of NOR administered, the epileptogenic activity decreases as the duration of infusion increases. Dose fractionation should therefore be recommended to prevent CNS side effects.