Linkage Analysis Using Co-Phenotypes in the BRIGHT Study Reveals Novel Potential Susceptibility Loci for Hypertension

Abstract

Identification of the genetic influences on human essential hypertension and other complex diseases has proved difficult, partly because of genetic heterogeneity. In many complex-trait resources, additional phenotypic data have been collected, allowing comorbid intermediary phenotypes to be used to characterize more genetically homogeneous subsets. The traditional approach to analyzing covariate-defined subsets has typically depended on researchers’ previous expectations for definition of a comorbid subset and leads to smaller data sets, with a concomitant attrition in power. An alternative is to test for dependence between genetic sharing and covariates across the entire data set. This approach offers the advantage of exploiting the full data set and could be widely applied to complex-trait genome scans. However, existing maximum-likelihood methods can be prohibitively computationally expensive, especially since permutation is often required to determine significance. We developed a less computationally intensive score test and applied it to biometric and biochemical covariate data, from 2,044 sibling pairs with severe hypertension, collected by the British Genetics of Hypertension (BRIGHT) study. We found genomewide-significant evidence for linkage with hypertension and several related covariates. The strongest signals were with leaner-body-mass measures on chromosome 20q (maximum LOD=4.24) and with parameters of renal function on chromosome 5p (maximum LOD=3.71). After correction for the multiple traits and genetic locations studied, our global genomewide P value was .046. This is the first identity-by-descent regression analysis of hypertension to our knowledge, and it demonstrates the value of this approach for the incorporation of additional phenotypic information in genetic studies of complex traits.

Hypertension (MIM 145500) is a major risk factor for kidney failure, stroke, and cardiovascular disease and is estimated to cause 4.5% of the global disease burden.¹ A familial disposition to high levels of systolic and diastolic blood pressure has been demonstrated,² which implies that there is genetic susceptibility to human hypertension. The British Genetics of Hypertension (BRIGHT) study has collected a resource of 1,634 families with at least two affected siblings (i.e., having severe hypertension) drawn from the upper 5% of the U.K. blood pressure distribution. A genomewide linkage scan was performed and identified regions of interest on chromosomes 2, 5, 6, and 9.³ Follow-up work has focused attention on chromosome 5q13.⁴ In common with other complex-trait resources, a variety of phenotypic covariate data, including biometric and biochemical measurements, were collected from these severely affected siblings (see BRIGHT Web site).

The aim of a primary genome scan in affected sibling pairs is the detection of regions of excess identical-by-descent (IBD) genetic sharing, but, in complex traits, the presence of genetic heterogeneity and phenocopies may dilute linkage signals. Phenotypic covariate data may carry information about comorbid characteristics, which offers the opportunity to reduce genetic heterogeneity and to identify novel linked loci. Researchers could select a comorbid characteristic, such as body mass, and choose to study leaner individuals with hypertension who might be expected to possess stronger genetic predisposition. This method could augment or unmask linkage signals, but it uses only a portion of the data set and relies upon dichotomization of a quantitative variable, on the basis of an often arbitrary threshold. In addition, application of more-stringent selection thresholds (which lead to higher expected proportions of genetic cases) leads to smaller data subsets, which may, in turn, lead to a corresponding attrition in power. The optimal threshold for a covariate is usually unknown, which leads to the temptation to try multiple thresholds and incur additional penalties due to multiple testing. An approach known as “ordered-subset analysis”⁵ can be used to identify the optimal threshold, by ranking families by some covariate and by finding the subset that maximizes the LOD score. However, it remains unclear how easily this methodology can be extended to multiple related covariates, such as anthropometric measures.

An interesting alternative strategy to subset analysis is to include the quantitative covariate directly in the linkage analysis.^6,7 This strategy offers the potential advantage that the within–sib pair covariate similarity and the mean covariate levels may be jointly studied. The results of such maximum-likelihood–based analysis can be conveniently expressed as a LOD score. However, the level at which this LOD corresponds to genomewide significance is not established, and, in practice, permutations of the covariate data are required to determine statistical significance.⁸ This determination requires the repeated maximization of a likelihood at each of many locations across the genome and is computationally slow. Indeed, computational burden becomes an increasing problem as more covariates are considered.

In contrast to maximum likelihood, score tests do not require estimation of the full model, so they are considerably faster to implement while maintaining the same local power as likelihood-ratio tests.⁹ Thus, they present a particularly attractive method when permutation is a consideration. In this article, we describe the development of a score test for the Rice-Holmans model and its application to multiple phenotypic covariates and genome-scan data from the affected sibling pairs in the BRIGHT study. This application offers the opportunity to fully exploit the extensive phenotypic characterization of this hypertensive resource while controlling for multiple statistical comparisons.

Methods

The Rice-Holmans Likelihood

The likelihood ratio for observed IBD sharing at any genetic location among a sample of affected sib pairs may be written as

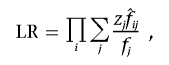where f_j and 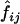are the prior and posterior IBD probabilities, respectively, that sib pair i shares j alleles IBD, and where z_j is the unknown probability that an affected sib pair shares j alleles IBD. If the IBD sharing of maternal and paternal alleles are assumed to be independent, then z_j may be expressed as a function of p, the probability that an affected sib pair share the allele they inherit from a given parent IBD. Assuming no parent-of-origin effect, we write z₀=(1-p)², z₁=2p(1-p), and z₂=p².

Covariates may be incorporated in the model by setting

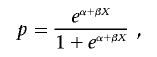where X denotes some vector of covariates and α and β are standard regression parameters for the intercept and slope, respectively. Holmans⁶ discusses two statistics,

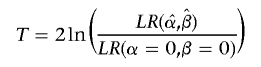and

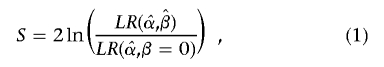where T is a test of linkage allowing for the effects of covariates and S is a test for dependence of IBD sharing on covariates. We consider it likely that a general test of linkage (without covariates) would be performed before a covariate analysis, in which case the latter statistic (a specific test for dependence of IBD sharing on covariate measures) would more likely be of interest. We shall, therefore, focus on developing a score test for this approach, although T is, in fact, a special case.

Development of a Score-Test Statistic

The likelihood for the Rice-Holmans model is¹⁰

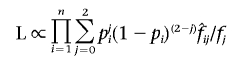with p_i=logit(e^α+βX_i), where X_i is some vector of covariates measured for sib pair i. We wish to test the null hypothesis H₀:β=0 against an alternative, H₁:β∈𝒞⊆ℜⁿ, where n is the number of covariates under testing, treating α as a nuisance parameter. Note that testing the null hypothesis corresponding to Holmans’s T statistic H^′₀:α=β=0 can be expressed as a special case, with α^′=0 and β^′=(α,β).

Let θ=(α,β) and X^′_i=(1,X_i). The first and second derivatives of the log likelihood under H₀ are, then,

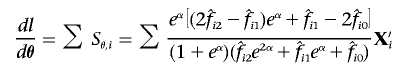and

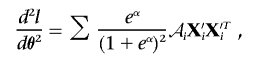where

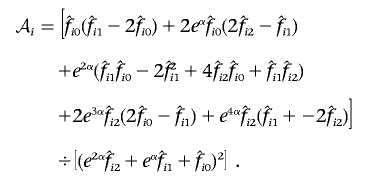Explicit forms for a generalized score test of H₁ against H₀, with allowance for parameter constraints and nuisance parameters, have been derived.^11–13 For the allowance of a nuisance parameter, the likelihood must be maximized under H₀ to find the maximum-likelihood estimate of α, 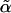. The vector S_θ,i is partitioned into S_α,i and S_β,i, according to the partitioning of θ. Let

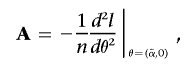and similarly partition A, so that

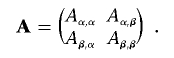Then, the score statistic is given by

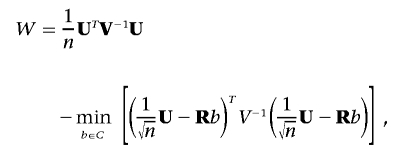where 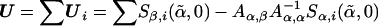, , 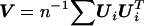and R=A_β,β-A_β,αA^-1_α,αA_α,β. Although the minimization may appear to negate the attractive properties of the score test stated above, this is a special case for which fast algorithms exist¹⁴ and can be solved much more quickly than a general minimization problem. Additionally, the minimum is always 0 when no constraints are placed on β.

Determining Genomewide Significance

Rather than assume a distribution for the score statistic (which might asymptotically be χ² or a mixture of χ², depending on the constraints¹⁵), we estimated it empirically by permuting the rows of the covariate matrix. Note that 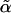at any locus is invariate to permutation and, so, needs to be calculated only once. To determine genomewide significance, we compared the maximum observed score statistic with its empirical distribution.

Significance in the Context of Testing Multiple Covariates

Studies will often collect multiple covariates, many of which will be correlated. The permutation procedure described above will generate a genomewide P value only for a single (set of) covariate(s). When multiple tests are being performed, we must take further action to maintain control of the familywise error rate (the probability of at least one false-positive result). A commonly used method is the application of a Bonferroni correction—multiplying each P value by the number of analyses undertaken—but this method is very conservative. A disadvantage common to this method and the more powerful sequential step-down and step-up procedures that have been suggested^16,17 is that each test is assumed to be independent. In practice, researchers may conduct multiple related tests (for example, in the case of a hypertension study, both of the related covariates serum creatinine and urea may be of interest).

We chose to calculate a global P value for the global null hypothesis—that genetic sharing among affected siblings is independent of any covariate—on the basis of the maximum observed score statistic across all genetic loci and covariates. Its distribution is easily estimated empirically (if permutations for each covariate are initiated with the same random seed) by the set of maximum score statistics across all covariates and genetic positions under each permuted data set. One attraction of this method is that it accounts naturally for any correlation structure between the covariates.

The Direction of Significant Results

If a significant result is found, it is of interest to know whether the increased IBD sharing is associated with increased or decreased levels of a covariate. In the context of score tests, this can be indicated by 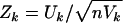for each covariate X_k. Z_k may be referred to a standard normal distribution, and its sign corresponds to the gradient of the likelihood surface at the null, so that a positive (or negative) Z_k indicates IBD-sharing increases with increasing (or decreasing) covariate k.

Subjects and Covariates in the BRIGHT Study

The 1,634 pedigrees in the BRIGHT study contain 2,044 affected full sibling pairs (3,376 individuals) from whom additional phenotypic covariate data were collected, including biochemical and biometric measures. Ascertainment and methods used for phenotyping and biochemical and urinary analyses are described elsewhere³ (BRIGHT Web site).

Other measures, including waist/hip ratio and BMI, were derived from these data, with the use of standard formulas. Although total serum calcium is conveniently measured, it is ionized calcium that is physiologically active. We used published formulas to estimate ionized calcium (“corrected calcium”)¹⁸ and the glomerular filtration rate (GFR),¹⁹ which is generally considered to be a better index of renal function than is serum creatinine concentration.

Construction of Pairwise Covariates

Since many of the covariates under study vary with age and sex, each was regressed on age and sex (allowing for an age-sex interaction), and the residuals were used as adjusted covariates in all subsequent analyses. For each adjusted covariate X measured on sibs 1 and 2, we defined 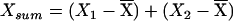and X_diff=|X₁-X₂| as pairwise covariates for the regression model, where 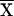is the mean of X in the entire sample. Thus, we are testing for dependence of IBD sharing on mean covariate levels and/or covariate similarity within a sibling pair. X_sum represents the mean covariate level for the sibling pair, so that β_sum≠0 would indicate dependence of genetic similarity on covariate values. X_diff represents the within–sibling pair covariate difference. If a covariate influences the propensity of a sib pair to exhibit linkage at a particular locus, genetic sharing would also be expected to be higher among siblings with more similar covariates (and would be identified by β_diff<0). The regression parameters were constrained so that α⩾0 and β_diff⩽0. This means that we did not allow mean genetic sharing to fall below that expected under the null or allow increasing covariate similarity to relate to decreased genetic sharing.

A problem common to all quantitative regressions is how to deal with outlying observations that may have a large influence on the test statistic. We decided it was inappropriate to drop outliers, since they may represent individuals with genuine but rare (in our sample) particular disease phenotypes. However, we also do not want to follow up results that depend on just a few families. Therefore, we conducted analyses of raw (X_diff and X_sum, as defined above) and ranked (X_diff and X_sum, replaced by their ranks) data that were interpreted in parallel.

Accommodating Missing Data

Only a minority of individuals had complete data for all covariates. It has been shown that statistical inference is more efficient if missing data are replaced by their expectation, given observed data, than if missing observations are dropped.²² Since intervariable correlations mean that information about the missing data exists in the complete data set, we imputed values for missing observations, using best-subset regression. Adjusted covariate data and age and sex for each sibling pair were used as explanatory variables, and the sum and difference variables were imputed. Inference using this mixture of observed and imputed data is valid, provided that the variance of any statistic is estimated appropriately, as with the robust-variance estimator described above.

Results

A total of 3,254 individuals (60% female) were included in this analysis. The mean age at recruitment was 60 (±SD 9.1) years, and 3,037 (93%) individuals were undergoing some kind of antihypertensive or lipid-lowering treatment, with 1,105 (34%), 398 (12%), and 131 (4%) taking two, three, or four or more distinct medications, respectively. A breakdown of antihypertensive medications is given in table 1. Summary statistics for all covariates studied are shown in table 2. Two covariates, urine albumin and albumin/creatinine ratio, showed strong positive skew and were log transformed.

Table 1. .

Antihypertensive/Lipid-Lowering Drug Treatment of Subjects in the BRIGHT Study

Medication	Na	Proportion (%)
β-Blocker	1,417	43.5
Thiazide diuretic	1,099	33.8
ACE inhibitor	1,020	31.3
Dihydropyridine Ca-channel antagonist	794	24.4
Statin	340	10.4
Loop diuretic	303	9.3
Other Ca-channel antagonist	156	4.9
α-Blocker	145	4.5
Centrally acting agent	50	1.5
A2-receptor antagonist	17	.5

^aNumber of subjects who reported each medication.

Table 2. .

Summary Statistics for Covariates Studied

Covariatea	Nb	Mean	SD	Median	Interquartile Range
Serum biochemistry:
Sodium (mmol/liter)	3,062	138.53	3.06	139.00	137.00–140.00
Chloride (mmol/liter)	3,062	102.03	3.13	102.00	100.00–104.00
Urea (mmol/liter)	3,082	6.07	1.71	5.90	5.00–6.90
Creatinine (μmol/liter)	3,083	89.56	20.47	87.00	77.00–99.00
Calcium (mmol/liter)	3,079	2.43	.13	2.43	2.35–2.51
Corrected calcium (mmol/liter)	3,082	2.34	.13	2.34	2.27–2.41
Albumin (g/liter)	3,071	44.47	2.84	44.00	43.00–46.00
GGT (U/liter)	3,071	34.44	30.75	26.00	19.00–38.00
Urate (mmol/liter)	3,071	.31	.08	.31	.26–.37
Total cholesterol (mmol/liter)	3,138	5.58	1.01	5.52	4.90–6.20
Tryglyceride (mmol/liter)	3,138	2.13	1.34	1.80	1.29–2.57
HDL cholesterol (mmol/liter)	3,138	1.36	.37	1.32	1.11–1.58
GFR (ml/min per 1.73 m2)	3,070	72.29	14.23	72.19	63.19–81.01
Urine biochemistry:
Sodium (24-h excretion) (mmol)	2,453	84.26	36.27	78.00	58.00–105.00
Potassium (24-h excretion) (mmol)	2,453	41.61	16.27	39.00	31.00–49.00
Creatinine (24-h excretion) (mmol)	2,452	6.39	3.03	5.60	4.30–7.80
Sodium concentration (mmol/liter)	2,440	141.33	59.89	132.60	100.30–172.65
Potassium concentration (mmol/liter)	2,439	69.90	26.65	67.60	52.50–83.70
Creatinine concentration (mmol/liter)	2,439	10.39	3.86	9.69	7.80–12.48
Creatinine clearance (ml/min)	2,308	82.33	29.80	79.17	63.33–96.81
Albumin (mg/liter)	2,452	13.73	68.47	5.00	3.00–8.00
Sodium/potassium ratio	2,453	2.16	.96	2.00	1.53–2.61
Urinary albumin/serum creatinine ratio (mg/mmol)	2,450	4.95	20.86	1.56	.90–3.11
Biometric measurements:
Triceps (cm)	2,831	18.84	8.77	18.00	12.00–25.00
Biceps (cm)	2,930	14.65	7.46	13.00	9.00–20.00
Subscapular (cm)	2,827	19.28	6.48	19.00	15.00–23.00
Suprailiac (cm)	2,886	18.91	6.45	18.00	14.00–23.00
Height (m)	3,250	1.66	.09	1.65	1.59–1.72
Weight (kg)	3,244	76.13	13.40	75.08	66.50–85.00
BMI	3,240	27.61	3.93	27.00	25.00–30.00
Mean waist (cm)	3,070	90.60	11.63	91.00	82.00–99.00
Mean hip (cm)	3,069	103.83	8.26	103.70	98.20–109.00
Waist/hip ratio	3,069	.87	.09	.87	.80–.94
Pulse and blood pressure measurements:
Pulse (beats/min)	3,250	68.44	11.93	68.00	60.00–76.00
SBP at phenotyping (mm Hg)	3,254	155.85	21.15	154.00	141.00–169.00
DBP at phenotyping (mm Hg)	3,254	93.56	11.39	93.00	86.00–101.00
SBP at diagnosis (mm Hg)	3,101	172.42	18.36	170.00	160.00–180.00
DBP at diagnosis (mm Hg)	3,101	104.57	8.83	103.00	100.00–110.00

^aGGT = γ-glutamyl transpeptidase; SBP = systolic blood pressure; DBP = diastolic blood pressure.

^bNumber of observations.

IBD Regression Results

We calculated genomewide significance levels, using score statistics and 10,000 permutations for each covariate. On a computer with a 2.6 GHz processor, maximizing the genomewide likelihood one time for a single covariate took ∼70 s. In contrast, permuting the data and calculating score statistics genomewide 10,000 times took only ∼35 min. Several covariates obtained a genomewide significant result (P<.05). To aid interpretation for geneticists who are more familiar with the LOD score in linkage, we also calculated LOD scores, defined by 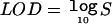, where S is as defined in equation (1). We present, in table 3, both P values and LOD scores for those results that were significant under both the raw and ranked analyses. More-complete results—all those that were significant under either analysis—are shown in table 4. Global P values (adjusted for the multiple traits and genetic locations studied) were .049 and .046 for the raw and ranked analyses, respectively.

Table 3. .

Results for Traits That Displayed Genomewide Significance (P<.05) for Both Raw and Ranked Analyses^[Note]

			Raw Data				Ranked Data
Covariate	Location	Marker	LOD	Z (Sum)	Z (Difference)	Minimum P	LOD	Z (Sum)	Z (Difference)	Minimum P
Anthropometric:
BMI	20q12	D20S107	2.71	−3.09	−2.49	.0202	3.04	−2.88	−2.81	.0232
Hip circumference	9q21	D9S273-D9S175	3.09	−.91	−3.56	.0212	2.91	−.83	−3.50	.0403
Hip circumference	20q11-20q13	D20S195-D20S119	3.26	−2.80	−3.21	.0035	4.25	−1.84	−4.11	.0015
Weight	20q11-20q13	D20S195-D20S178	3.70	−3.33	−3.23	.0023	3.96	−2.95	−3.60	.0026
Serum chemistry:
Creatinine	5p13-5q12	D5S426-D5S427	3.29	−4.60	−3.19	.0015	3.51	−3.77	−2.41	.0070
GFR	5p13-5q12	D5S426-D5S427	3.70	3.80	−1.29	.0032	3.71	3.90	−1.38	.0050
Urea	5p13-5q11	D5S426-D5S1969	3.29	−4.24	−1.68	.0059	3.15	−3.89	−.76	.0149
Urine chemistry:
24-h Creatinine	13q22	D13S156-D13S1812	2.49	1.58	−2.40	.0472	2.83	2.22	−2.53	.0252

Note.— Z statistics for the sum and difference covariates may be referred to a standard normal distribution.

Table 4. .

Results for Traits That Displayed Genomewide Significance (P<.05) for Either Raw or Ranked Analysis^[Note]

			Raw Data				Ranked Data
Covariate	Location	Marker	LOD	Z (Sum)	Z (Difference)	Minimum P	LOD	Z (Sum)	Z (Difference)	Minimum P
Anthropometric:
BMI	20q12	D20S107	2.71	−3.09	−2.49	.0202	3.04	−2.88	−2.81	.0232
Height	21q22.3	D21S266	…	…	…	…	3.18	−1.05	−3.84	.0145
Hip circumference	9q21	D9S273-D9S175	3.09	−.91	−3.56	.0212	2.91	−.83	−3.50	.0403
Hip circumference	20q11-20q13	D20S195-D20S119	3.26	−2.80	−3.21	.0035	4.25	−1.84	−4.11	.0015
Waist circumference	9q21.13	D9S175	2.84	−2.30	−2.91	.0225	…	…	…	…
Weight	20q11-20q13	D20S195-D20S178	3.70	−3.33	−3.23	.0023	3.96	−2.95	−3.60	.0026
Serum chemistry:
Albumin/creatinine ratio	9q33.1	D9S1776	…	…	…	…	3.05	−3.36	−2.33	.0229
Chloride concentration	9q34.3	D9S312-D9S1826	…	…	…	…	3.43	−2.37	−2.90	.0070
Chloride concentration	14q11.2	D14S283	…	…	…	…	3.15	−2.03	−2.69	.0315
Total cholesterol	16p12.3	D16S3103	…	…	…	…	3.10	−3.59	−1.23	.0285
Corrected calcium	2p22-2p21	D2S367-D2S2259	…	…	…	…	2.85	−1.12	−3.53	.0203
Creatinine	5p13-5q12	D5S426-D5S427	3.29	−4.60	−3.19	.0015	3.51	−3.77	−2.41	.0070
GFR	5p13-5q12	D5S426-D5S427	3.70	3.80	−1.29	.0032	3.71	3.90	−1.38	.0050
Sodium	15q26.2	D15S657	…	…	…	…	2.56	3.59	−.89	.0350
Tryglyceride	13q31.3	D13S265	2.65	−2.57	−4.67	.0259	…	…	…	…
Tryglyceride	13q33.1	D13S158	3.04	−2.03	−4.42	.0473	…	…	…	…
Urea	5p13-5q11	D5S426-D5S1969	3.29	−4.24	−1.68	.0059	3.15	−3.89	−.76	.0149
Blood pressure phenotypic measures:
SBP at diagnosis	15q12	D15S986	2.32	−3.09	−.71	.0454	…	…	…	…
DBP at phenotyping	3q13.31	D3S1278	2.76	−1.39	−3.48	.0202	…	…	…	…
DBP at phenotyping	15q23	D15S131	2.94	3.73	.11	.0136	…	…	…	…
Pulse at phenotyping	6q27	D6S264-D6S503	3.00	−1.18	−3.78	.0143	…	…	…	…
Pulse at phenotyping	15q26.2	D15S130	…	…	…	…	2.86	−2.64	−3.12	.0273
Urine chemistry:
Albumin/creatinine ratio	1q43	D1S2785-D1S2842	2.65	−3.94	−1.16	.0260	…	…	…	…
Albumin/creatinine ratio	9q33.2	D9S1682	…	…	…	…	2.74	−3.53	−1.55	.0298
24-h Creatinine	13q22	D13S156-D13S1812	2.49	1.58	−2.40	.0472	2.83	2.22	−2.53	.0252
Urine creatinine concentration	13q22	D13S156-D13S1812	…	…	…	…	2.94	2.22	−2.97	.0255
24-h Sodium	4p16.3	D4S412	3.24	.05	−3.75	.0106	…	…	…	…

Note.— Z statistics for the sum and difference covariates may be referred to a standard normal distribution.

Follow-up work on our primary genome scan revealed a region of suggestive linkage (LOD=2.5) on chromosome 5q13.⁴ Inclusion of at-phenotyping systolic (but not diastolic) blood pressure led to an increase in evidence for linkage in this region, although it did not achieve genomewide significance.

Analysis of Independent Sib Pairs

The likelihood model is expressed in terms of pairwise sharing, and a proportion of recruited families included more than two affected siblings. In this case, the genetic sharing and covariate data are not independent between sibling pairs in the same family, and it is difficult to account for a variety of family sizes in any permutation routine. This is a long-standing problem in analysis of sibling-pair data.²³ Therefore, to confirm that our results are not due to any problem introduced by ignoring nonindependence, we reran all analyses, selecting at random a single sibling pair from each family. The pattern of results was very similar, with mean correlation between score statistics from the independent and nonindependent sib pair analyses of 0.98 and identification of significant linkage for the same locations (data not shown). This analysis of independent sib pairs also achieved borderline genomewide significance for the raw and ranked analyses (P=.053 and P=.051, respectively).

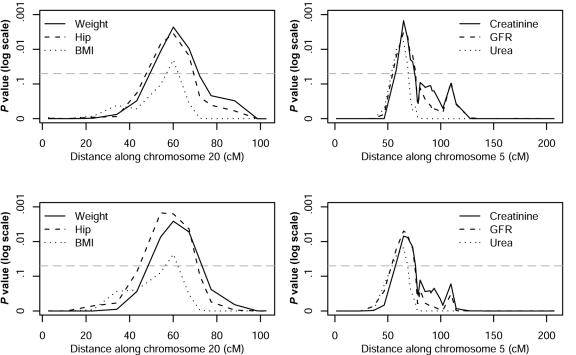
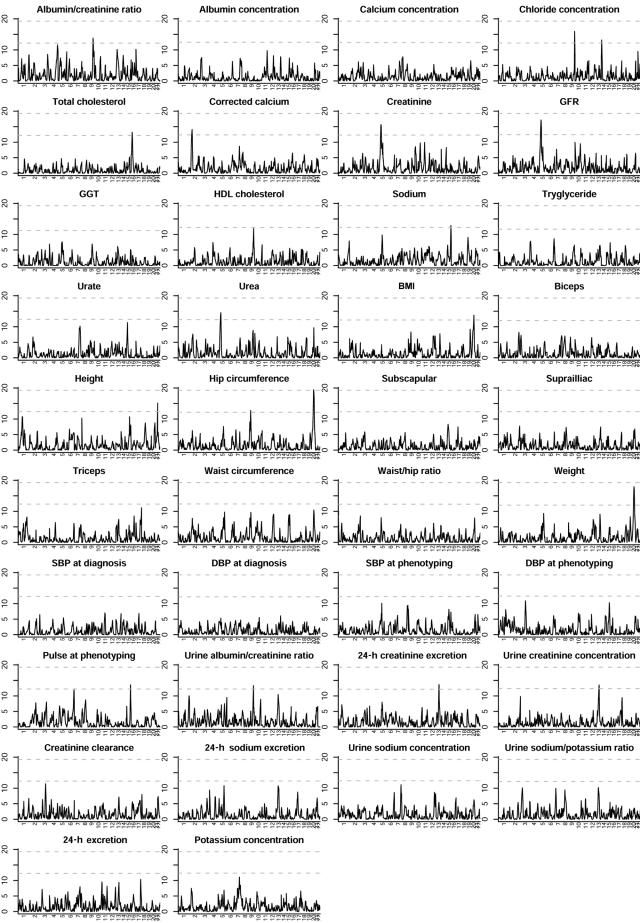
There were four regions that achieved genomewide significance in both the raw and the ranked analyses. The weaker signals were from hip circumference on chromosome 9q and increased total creatinine excretion on chromosome 13q. However, of particular interest were linkage signals found with two clusters of related measures. We found linkage to a 28-Mb region on chromosome 20q11-20q13 when the body-mass measures weight, BMI, and hip circumference were included in the analysis (minimum genomewide P=.002). This linkage is associated with leaner body mass: genetic similarity increases as the mean body mass of the sib pair decreases. We also found linkage to a 36-Mb region on chromosome 5p13-5q12 when the kidney function–related covariates serum creatinine, serum urea, and GFR were studied (minimum genomewide P=.002), although GFR showed significant linkage only in the ranked analysis. In this case, the linkage is associated with increasing measures of kidney function—higher GFR and lower serum creatinine and urea. For all these covariates, increasing linkage was also associated with increasing trait similarity between sibs. The P values for these traits and chromosomes are shown in figure 1. Genomewide score statistics for analysis of all ranked covariates studied are shown in figure 2.

Figure 1. .

P values for body mass and renal function–related traits that achieved genomewide significance on chromosomes 20 and 5, respectively. The results of the analysis of raw residuals and ranked data are shown in the top and bottom panels, respectively. The dotted line indicates the genomewide 5% significance threshold.

Figure 2. .

Genomewide score statistics for analysis of all ranked covariates studied. The score statistic is shown on the vertical scale. The upper and lower horizontal dashed lines represent the adjusted and unadjusted, respectively, thresholds for genomewide significance for the multiple covariates. GGT = γ-glutamyl transpeptidase; SBP = systolic blood pressure; DBP = diastolic blood pressure.

We chose to focus on the two clusters on chromosomes 5p13-5q12 and 20q11-20q13, for four reasons: the signals (1) come from analyses using multiple related traits, (2) are exhibited over several neighboring markers, (3) are present in both the raw and the ranked analyses, and (4) coincide with the smallest genomewide P values observed.

Discussion

We have developed a score test to facilitate the computationally efficient application of IBD regression for the simultaneous analysis of multiple covariates in sibling pairs severely affected with hypertension. An attraction of this approach is that it tests for excess or reduced allele sharing by capitalizing on all the phenotypic covariate data.

Our results identify two new loci linked to hypertension and specific anthropometric features that characterize leaner body habitus and to covariates for normal (or supranormal) renal function, which collectively attain genomewide significance. These regions were not implicated in the primary genome-scan analysis of hypertension alone.

We consider two alternative scenarios that would lead to deviation from our null hypothesis. The first is that the linkage signals arise from disease genes that were masked because of genetic heterogeneity or the presence of phenocopies. Since increased body mass and impaired renal function act as independent risk factors for hypertension, a subgroup of siblings who are leaner or who have retained normal renal function may be more homogeneous, in terms of genetic factors causing essential hypertension. Therefore, one explanation for our findings is that we have homed in on hypertensive loci that influence blood pressure through nonobesity or nonrenal dependent mechanisms. The alternative scenario, in which we would also expect deviation from our null hypothesis, relates to a locus that directly affects the covariate under study. Therefore, an alternative explanation for our findings is that we have identified loci that influence body mass or renal function directly, either within individuals with hypertension or within the general population. We evaluate our results in the light of data from experimental models and other human studies, to consider the biological plausibility of each explanation, but further work will be required to choose between these possibilities, since our data alone do not allow one to be distinguished from the other.

Our first linkage cluster was identified through analysis with three body-mass–related traits on chromosome 20q11-20q13 (weight, hip circumference, and BMI). Obesity is a phenotype that commonly accompanies hypertension and is an independent cause of high blood pressure, which also increases target organ damage. We first explore the possibility that we have identified a locus that directly influences body mass. Several studies of obesity-related traits have shown coincident linkage to an overlapping region on 20q13,^24–27 suggesting that our results may relate to the same locus. However, a search of the genes in our region revealed no clear candidate genes for control of weight gain or loss, with the exception of the lipin 3 (MIM 605520) gene, which may potentially play a role in metabolic disorders characterized by insulin resistance (another member of the lipin family, lipin 1 [MIM 605518] on chromosome 2, has been associated with lipodystrophy). Additionally, a search of the Rat Genome Database revealed no reports of weight-related loci in the syntenic region. Our population differs from those in the linkage studies of obesity, in that all individuals have severe hypertension but are generally not obese (median BMI=27), diabetics were excluded during recruitment, and linkage increased with decreasing body mass, so that this signal comes from lean individuals with hypertension. We, therefore, believe it more likely that this signal reflects linkage to hypertension among lean individuals rather than a locus responsible for a general predisposition to lower weight, body mass, and hip circumference. Further support comes from our bioinformatic searches, which reveal that there are several candidate genes within this interval that might influence blood pressure. The strongest candidates include the prostacyclin synthase gene (PTGIS [MIM 601699]) and the sodium-hydrogen exchanger 8 (SLC9A8), both located at 20q13.13. PTGIS encodes the enzyme prostacyclin synthase, which catalyzes the isomerization of prostaglandin H2 to prostacyclin, which is a potent vasodilator and inhibitor of platelet aggregation, whereas sodium/hydrogen exchangers have a central role in sodium excretion in the kidney.²⁸

The second linkage cluster, on chromosome 5p13-5q12, was identified through analysis with three indicators of renal function, which is itself a key determinant of blood pressure level. This locus is neighboring but distinct from the chromosome 5q13 locus identified by our primary genome scan.⁴ To our knowledge, no other linkage scans for kidney function among humans with hypertension have identified this region. This combination of covariate features (higher calculated GFR and lower serum creatinine and urea) is often seen in early nephropathy associated with metabolic syndrome and diabetes.²⁹ In this pathological process, an initial phase of supranormal renal function is associated with endothelial damage, leading to microalbuminuria and, eventually, to nephron loss. We know that, in early diabetic nephropathy, deterioration of renal function can be delayed with very tight blood pressure control.²⁹ These features of high GFR and low urea and creatinine have not been observed to date in hypertensive nephrosclerosis.

Again, we cannot discount the possibility that we have identified a locus directly responsible for kidney function. Of the genes in this region, the prostaglandin E receptor 4 (EP4 [MIM 601586]) on chromosome 5p13.1 has been shown to be expressed in rat kidneys and has a potential mechanism to influence kidney function. The effects of prostaglandin E2, which is involved in the maintenance of kidney function and renal blood flow during physiological stress, are mediated through EP4.^30,31 However, in support of a hypertension locus, it is notable that the syntenic region on rat chromosome 2 contains several rat blood pressure–related loci, and comparative genomics work has suggested that human chromosome 5p13.1 is a target region for human hypertension.^32,33 There are also a number of candidate genes in this region that may affect blood pressure through vascular rather than renal pathways. These include the gene encoding phosphodiesterase 4D (PDE4D [MIM 600129]), which localizes to chromosome 5q12, and, toward the opposite end of our identified region, the gene that encodes the natriuretic peptide receptor C, NPR3 (MIM 108962), at 5p14-5p12. Fine-mapping of an ischemic stroke–susceptibility locus identified through linkage³⁴ found significant evidence of association to PDE4D, and variants in NPR3 have been shown to affect blood pressure in mice.³⁵ Further work will be required to evaluate candidate genes in this region that might affect blood pressure and/or renal function.

The majority of subjects were being treated for high blood pressure when they were phenotyped. Such treatment affects not only blood pressure but also pulse and many biochemical covariates. Various methods have been proposed to adjust for treatment effects, in an attempt to reconstruct the blood pressure or covariate that would be observed were the individual not undergoing treatment.^20,21 However, all methods involve simplifying assumptions that may not hold in practice—in particular, that the distribution of the variable in the treated individuals would be the same, were they not treated, as its distribution among untreated individuals. Since these variables are monitored for effects of treatment, and treatment is varied accordingly, this assumption cannot hold. Further, issues of noncompliance (i.e., individuals report taking, but do not take, medication) and nonresponse (i.e., drug treatment does not produce the expected effect on the variable) are ignored. Additional problems are introduced for individuals on more than one treatment, by complex interactions between different drugs on biochemical variables. For example, it is not clear in what direction one might adjust high-density lipoprotein (HDL) cholesterol were an individual on both β-blocker and α-blocker treatments, since the former acts to decrease and the latter to increase HDL cholesterol. The alternative to adjustment—ignoring the effects of drug treatment—introduces additional noise, which can impair our ability to detect genuine signals but has been shown not to lead to any increase in type I error rates.²⁰ Therefore, although we are aware that this may impede our ability to detect genuine signals, we have chosen to use unadjusted blood pressure, pulse, and biochemical covariates in our analyses rather than to employ adjustments based on assumptions that may not be justifiable in practice.

Essential hypertension is a multifactorial trait, and the search for its genetic determinants has been hampered by the inability of researchers to discriminate between affected individuals who have differing genetic risk factors. We have developed a computationally efficient method for incorporating covariate data into affected-sib-pair linkage analysis. This method has allowed us to identify regions of the genome where genetic sharing between affected siblings is related to their covariate similarity as well as to their mean covariate levels—specifically, regions on chromosome 20q11-20q13 related to body mass and regions on chromosome 5p13-5q12 related to renal function. These regions have not been linked elsewhere to hypertension in humans, but the evidence suggests they are worthy of further research.

IBD regression offers the potential to maximize the value of comorbid characteristics in family-based–linkage data sets, without restriction to investigator-defined subsets. This strategy is readily applicable to other complex traits where multiple covariate phenotypes have been collected. Our results suggest that there may be additional important findings locked within complex-trait data sets and that this computationally efficient application may reveal new areas of research inquiry.