How Does Running Memory Span Work?

Abstract

In running memory span, a list ends unpredictably and the last few items are to be recalled. This task is of increasing importance in recent research. We argue that there are two very different strategies for performing running span tasks: a low-effort strategy in which items are passively held until the list ends, when retrieval into a capacity-limited store takes place; and a higher-effort strategy in which working memory is continually updated using rehearsal processes during the list presentation. In two experiments, we examine the roles of these two strategies and consequences of two types of interference.

How Does Running Span Work? The Quest to Measure Memory Capacity

In running memory span (Pollack, Johnson, & Knaff, 1959), each list continues for an unpredictable number of items, after which items from the end of the list are to be recalled. The mechanism of running span is of recent interest because this task has led to competing inferences about working memory. For example, Postle (2003) used a version of running span as an updating task to demonstrate the effects of episodic context, whereas Cowan, et al. (2005) assumed that information was passively received until the list ended, at which time attention was used to transfer information to a categorical form. The mechanism is important inasmuch as running span yields substantially higher correlations with intellectual aptitudes than does the digit span task used in intelligence tests (Cowan et al., 2005; Mukunda & Hall, 1992). A potentially critical factor is that Postle presented items at a slow, 3.5 s per item rate, whereas Cowan et al. presented items at a fast, 0.25 s per item rate. We examine the rate variable in Experiment 1.

It is often difficult to draw specific conclusions about processing from serial recall tasks. There are multiple hypotheses concerning the importance of interference from subsequent list items during input and from prior list items during recall, the means of maintaining items in memory, and the means of maintaining the correct serial order of items (e.g., Cowan, Saults, Elliott, & Moreno, 2002; Farrell & Lewandowsky, 2004). One complicating factor is that participants can use their knowledge of the list length to group and rehearse items (e.g., Anderson & Matessa, 1997; Ng & Maybery, 2005). However, that factor appears to be reduced in running span tasks because of the unpredictability of the list’s end and proactive interference from items earlier in the list (e.g., Hockey & Hamilton, 1977).

Still, one can imagine at least two methods of executing running span. The participant might keep track of the last few items, dropping older ones and adding new ones in an updating process (Postle, 2003). This has been the default assumption. Alternatively, though, the participant might perceive the items passively, letting them enter into some type of storage that does not require special mnemonic processing and, when the list ends, attempt to recall as many items as possible from passive storage. This might entail the transfer of information from phonological or sensory store to a more categorical form (Cowan et al., 2005).

Hockey (1973) demonstrated that the rate of presentation makes an important difference for how running span is carried out. Lists were presented at either a slow or a fast rate and participants were instructed either to try to rehearse items or to listen passively until the list ends. With a slow rate, participants did better when asked to rehearse whereas, with a fast rate, participants actually did better when asked to listen passively until the list ended. To observe potential benefits of rehearsal, therefore, in Experiment 1 we compared running span with relatively slow versus fast presentation and looked for enhanced performance with slow presentation.

We expected that the last 3 or 4 items typically would be retrieved without effort and that the items just before those often could be maintained using rehearsal. These expectations are based on an assumption that there is a core capacity of 3 to 4 separate units or chunks of information in adults. This capacity limit, smaller than Miller’s (1956) limit of seven or so items, is found in many studies in which rehearsal and the grouping of units to form larger chunks is impractical, preventing multi-item chunking (Broadbent, 1975; Cowan, 2001; Mandler, 1985); and also studies in which associated words are presented in serial recall to provide chunks of a known size (Chen & Cowan, 2005; Cowan et al., 2004; Glanzer & Razel, 1974; Tulving & Patkau, 1962).

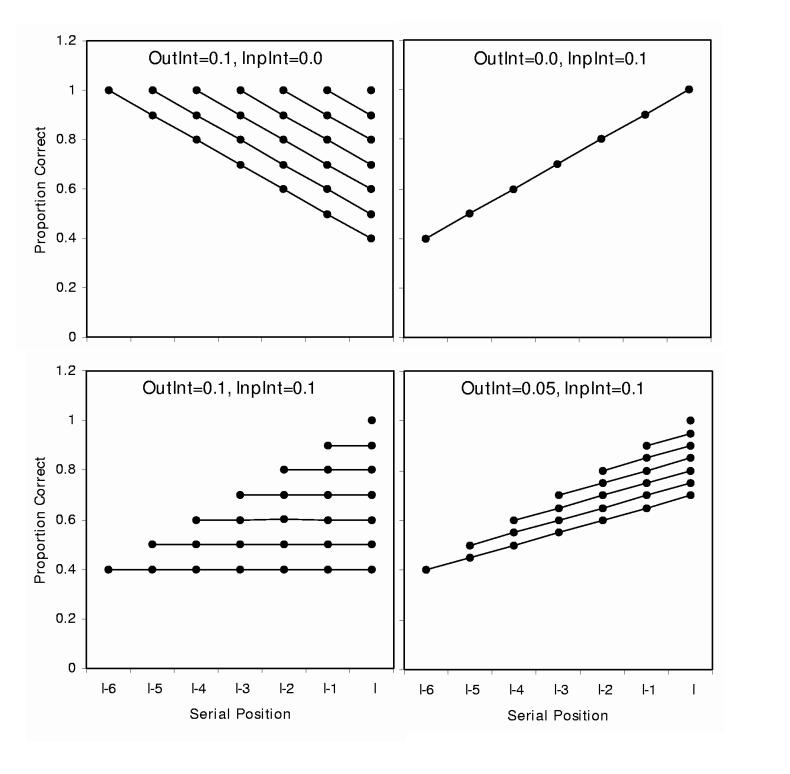
We were concerned about effects of input and output interference on running memory span, which we examined much as Cowan et al. (2002) did for fixed-length lists. We cued recall to begin at the last serial position (I) or at some prior position I-1 through I-6, always continuing until the end of the list. If there were no effect of interference from items presented after a particular item within the list (i.e., a type of retroactive interference that we term input interference), then the first-recalled item would be at the same level no matter what its serial position. Consistently greater-than-zero input interference should result in a rising curve across serial positions for the first-recalled item (a recency effect as in hypothetical Figure 1, top right panel). Also, if there were no interference from the participant’s prior recall on the trial (i.e., output interference), then the item in a particular position I-i would be recalled equally well no matter how many items preceded it in recall. Consistently greater-than-zero output interference should result in separate serial position curves for each beginning point of recall. In particular, performance at any Serial Position I-i should be better when recall starts at Serial Position I-i-x than when recall starts at an earlier Serial Position I-i-(x-y), for all y >0 (as in Figure 1, top left panel). The overall pattern of recall depends on the combination of input and output interference effects, with two hypothetical examples shown in the bottom panels of Figure 1.

Figure 1.

Simple hypothetical predictions of performance by serial position under different combinations of interference from subsequent items in the list, or input interference (InpInt), and interference from the participant’s own responses, or output interference (OutInt). The values of InpInt and OutInt refer to the amount deducted from the proportion correct for every item intervening between the presentation of an item and the appropriate time of recall of that item.

If the slow-paced running span task promotes rehearsal during presentation of the list items and the fast-paced task prevents it, then the slow paced task should offer less evidence of input interference. To assess this, we devised a probed-recall technique. After each list of spoken digits, a recall cue prompted recall of the last X items (1≤X≤ 7). This yielded a response pattern capable of separating input and output interference effects (see Figure 1).

EXPERIMENT 1

Method

Participants

Twenty-five native English speaking, University of Missouri undergraduates (13 female, 12 male) with normal or corrected-to-normal vision and unimpaired use of their dominant hand participated in exchange for course credit.

Apparatus, Stimuli, and Procedure

Participants were tested in a single session lasting under 50 min. The pace of the running span task was manipulated within participants, with counterbalancing for task order. For both the fast- and slow-paced tasks, there were 6 practice trials followed by 70 test trials, which included 10 trials (2 of each running span list length) per probed set size. A response was scored correct only for a digit placed in the blank indicating its correct serial position relative to the end of the list.

We presented stimuli by computer at a viewing distance of about 50 cm. The running memory span task was adapted from Cohen and Heath (1990), but the probed procedure was our own. The digits 1-9 were digitally recorded in a male voice and compressed to play within 250 ms each, without a change in fundamental frequency, using the SoundEdit 16 program (Macromedia, San Francisco, CA). They remained easily identifiable, as in compressed-speech advertisements. These digits were played over headphones at 66-68 dB (A).

The instruction was to try to remember the last seven digits in each list and, when the list ended, recall the most recent X digits (1≤X ≤7) as indicated by the response display. Each trial was initiated by the participant’s keypress. Immediately thereafter, a prompt (“+”) appeared for 1 s, after which a spoken list began. The list included 12, 14, 16, 18 or 20 random digits (from the set 1-9) presented via computer at either a fast pace of 0.25 s/digit or a slow pace of 1 s/digit. Throughout each list, there were restrictions on the random occurrence of digits: a digit was never repeated within a moving window of seven consecutive digits, no digit was repeated more than twice, and no two digits appeared in forward numerical order. A row of vertically-centered dots (“•”), one per digit, appeared from the left side of the screen as the digits were played. A probed recall procedure prompted recall of the last 1, 2, 3, 4, 5, 6 or 7 items. Just 250 ms after the list ended, the dots were replaced with the spoken digits and one blank per to-be-recalled item. For example, if given the series, “4, 8, 3, 9, 5, 2, 1, 7, 6, 3, 8, 5” in a 4-item recall condition, participants would see “4, 8, 3, 9, 5, 2, 1, 7, _, _, _, _”. The blanks were filled from left to right with digits, using the computer’s numerical key pad. Participants pressed “enter” following each digit, or to leave a blank and advance to the next item. Responses could be edited before but not after pressing “enter”.

At the end of the session, many of the participants answered several questions about the strategy that was used.

Results and Discussion

The independent variables were pace of the running span task (fast and slow) and probed recall set size (1 through 7). The dependent variables of interest were accuracy on the running span task and mean typing time per correct response.

Accuracy

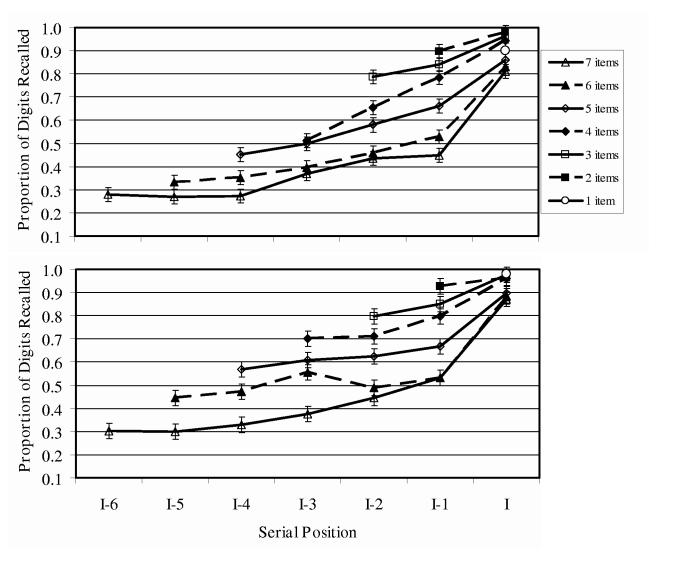
When there were only 1-3 items to recall (Serial Positions I-2 through I), performance appears similar in the fast and slow presentation conditions (Figure 2, top and bottom panels, respectively). However, the slower presentation rate facilitated performance for the lists with 4 to 6 items to be recalled, especially in Serial Positions I-5 through I-3.

Figure 2.

Proportion Correct with fast presentation rate (top) and slow presentation rate (bottom) in Experiment 1. Error bars represent 95% within-subject confidence intervals (Loftus & Masson, 1994).

ANOVAs on accuracy, performed separately for each probed recall set size, included within-participant effects of serial position (the number of levels depending on the set size) and presentation pace. Based on prior research (Cohen & Heath, 1990), we would not expect an effect of the total number of running span items (unless the number of items were in the vicinity of span; see Postle, 2003), and we collapsed the data across our range of 12-20 items. The significant main effect of serial position, which appears as a strong recency effect in both panels of Figure 2, is typical of running span; the long list of irrelevant digits preceding the recall set is highly detrimental to memory for primacy items. The main effect of presentation pace was significant only in the case of 1-item recall, F(1, 48) = 7.44, p < .01, partial eta squared (η_p²) = .134.

The effect of primary interest was the interaction between presentation pace and set size, significant in the cases of the 4- and 6-item recall, F(3, 144) = 5.68, p <.001, η_p² = .106, and F(5, 240) = 2.39, p < .04, η_p² = .047, respectively. The failure to detect this interaction for 5-item recall may be a power issue, F(4, 192) = 1.43, p = ns, η_p² = .029. If so, there appears to be a region 4 to 6 items back for which slow presentation helps, probably because of rehearsal. Of the 28 serial position-output interference combinations, separate t tests for each combination yielded a significant advantage for the slow presentation pace for Serial Positions I-3, I-4, and I-5 within recall sets of 4, 5, or 6 items. Table 1 shows the slow-fast difference scores in proportion recalled for each of the 28 combinations, and illustrates that difference was significant in a 1-tailed test (shown in bold) whenever the items fourth, fifth, or sixth from the end of the list were to be recalled first. Thus, in particular, for the I-3 item in 4-item recall set, recall was significantly better in the slow paced than fast paced condition, M_difference = .19, t = 3.24, p < .05. Recall of the I-3 and I-4 items in 5-item recall was also better in the slow paced than fast paced condition, M_difference = -.11, t = 1.81, p < .05, and M_difference = -.12, t = 1.73, p < .05, respectively. In 6-item recall, the I-3, I-4 and I-5 items all benefited from rehearsal in the slow paced condition, M_difference = -.16, t = 2.44, p < .05, M_difference = -.12, t = 2.06, p < .05, and M_difference = -.11, t = 1.84, p < .05, respectively.

Table 1.

Difference between Proportion Correct in Slow – Fast Conditions.

Recall Set Size	Serial Position
	I-6	I-5	I-4	I-3	I-2	I-1	I
1							0.08
2						0.03	-0.02
3					0.01	0.01	0.01
4				0.19	0.06	0.01	0.02
5			0.12	0.11	0.04	0.01	0.04
6		0.11	0.12	0.16	0.03	0.00	0.05
7	0.02	0.03	0.06	0.01	0.01	0.08	0.06

Note. Differences in bold are significant by t test (df = 24), p < .05 (one-tailed).

Several methods of rehearsal are consistent with these findings. It could be that participants rehearse Serial Positions I-3 through I, and then suffer gradual output interference for these rehearsed positions. However, it also is possible that they rehearse I-4 through I, with more severe output interference. It also is possible that they do not rehearse all the way through I. For example, they might only rehearse I-4 and I-3. These rehearsal scenarios all share the feature of rehearsal of Item I-3, where the largest benefit of slow presentation occurs. Rehearsal presumably offers no help for the last three items, because one can remember them just as well on a passive basis. While we do not know if participants actually rehearsed Serial Positions I-2 through I in the slow-paced condition, we know that they remembered them just as well without the opportunity for rehearsal, in the fast-paced condition.

When trying to recall seven items, interference may be too great for the aftereffects of rehearsal to last, as indicated by the failure to detect any difference in recall between the fast and slow paced conditions for this set size.

Response Time

We examined mean reaction time, the time it took participants to type each digit of their response, for correct responses only. In general, the time spent on the first item in recall was significantly longer in the slow than the fast condition. In fact, as is shown in Table 2, the mean difference was as great as 1838 ms for 7-item recall. Separate t-tests for each of the 28 serial position-output interference combinations confirm that the fast-slow difference was significant for the first item in each recall set, as shown by bold entries in Table 2.

Table 2.

Difference between Reaction Time (ms) on Correct Responses in Slow – Fast Conditions.

Recall Set Size	Serial Position
	I-6	I-5	I-4	I-3	I-2	I-1	I
1							394
2						499	145
3					332	65	134
4				599	295	-32	144
5			433	75	-240	23	-117
6		906	-65	54	14	39	244
7	1838	329	-235	-262	-133	-168	131

Note. Differences in bold are significant by t test (df = 24), p < .05 (one-tailed).

These differences in response time indicate that different cognitive processes are at play in fast and slow paced running span. In the slow paced condition, where response times were longer, it is possible that participants used the time to wrap up rehearsal or to integrate their rehearsed response with just-presented items. Most importantly, the response time patterns offer reassurance that the lower span scores for the fast-paced condition are not due to decay during a lag in response time.

Perceived Difficulty

As part of the debriefing process, first few participants were asked to comment on the difficulty of the task in general. A common response was that the fast-paced task was perceived to be less difficult than the slow-paced task. We implemented a more formal questionnaire for the remaining participants. In response to the open-ended question, “Did you find one of the tasks easier than the other,” 16 of 20 respondents to the questionnaire indicated that the fast task was easier, while just 4 of 20 respondents indicated that the slow task was easier; a significant difference, t(df = 19) = 3.27, p < .01. No one indicated that they were equally difficult. Ironically, even those who thought the fast task was easier actually did slightly better in the slow task, M_difference (and SD_difference) for recall set sizes 1 through 7 = -0.02 (0.07), 0 (0.14), 0 (0.31), 0.30 (0.35), 0.25 (0.85), 0.44 (0.73), and 0.37 (0.66), respectively. The differences are significant for set sizes 4, 6, and 7 by paired-samples t-tests (2-tailed), t(df = 15) = 3.33, 2.40, and 2.23, respectively, p’s < .05. This was true also of the 4 participants who correctly thought that the slow pace was easier. We suspect that “easier” for 16 participants was taken to reflect how little active processing they had to do; rehearsing (in the slow condition) is not as easy as listening passively (in the fast condition), even though rehearsing improves performance.

Experiment 1 suggests that running span was not an updating task when the items were presented at a rapid rate and hence could not be rehearsed. Rehearsal benefits (reflected in the performance difference between fast and slow presentation) appear to hold for the region four to six items from the end of the list. The benefit is lost for the seven-item recall set, probably due to output interference. The data also indicate that the last three items from the end of the list do not benefit from rehearsal, probably because they are readily retrievable through a passive strategy.

The pattern of steady increase across serial positions indicates effects of input interference; recall of each item is reduced by the presence of subsequent list items. At the same time, the pattern of separation of serial position functions for different recall set sizes indicates effects of output interference; recall of the item at any particular serial position is reduced when it follows the recall of more prior list items. Rehearsal in the slow paced condition appears to make the serial position functions shallower, but does not diminish the separation between functions of different recall set sizes. This suggests that rehearsal combats input interference but not output interference (refer to Figure 1).

EXPERIMENT 2

The nature of output interference effects in Experiment 1 is unclear because of the instruction to report a specified number of digits. When a list ends, it could be that the participant at first retains the necessary number of digits in memory but that the reporting process degrades not-yet-recalled digit memory representations. Alternatively, what creates output interference could be the need to respond in a fixed number of slots, if it exceeds the number of digits actually in memory. The participant might guess at a digit and, in doing so, interfere with memory for digits later in the list.

We were able to address this question using running span data from Cowan et al. (2005, Experiment 1) that they did not examine by serial position. Cowan et al. included two types of procedure: one in which the number of digits to be recalled was fixed within a trial block, and one in which the participant was to recall only as many digits from the end of the list as he or she could remember, up to the number of answer spaces provided. The latter procedure drastically reduces the tendency to guess at digits that were not remembered.

Method

The participants (N = 66: 41 female, 25 male) always received the fast (0.25 s/item) presentation rate of digits. The first procedure required that a certain number of items from the end of the list be recalled; the participant was to guess at digits that were not recalled. There were three trial blocks, with 5, 6, and 7 answer spaces per trial, respectively. After that, the second procedure allowed that the participant could recall as many or as few digits from the end of the list as could be remembered, up to the number of answer spaces provided (in separate trial blocks, 7, 6, and then 5 spaces). Answers in this procedure were right-justified for scoring. Each of the six trial blocks included two practice and nine test trials. Cowan et al. (2005, Experiment 1) described the method further.

Results and Discussion

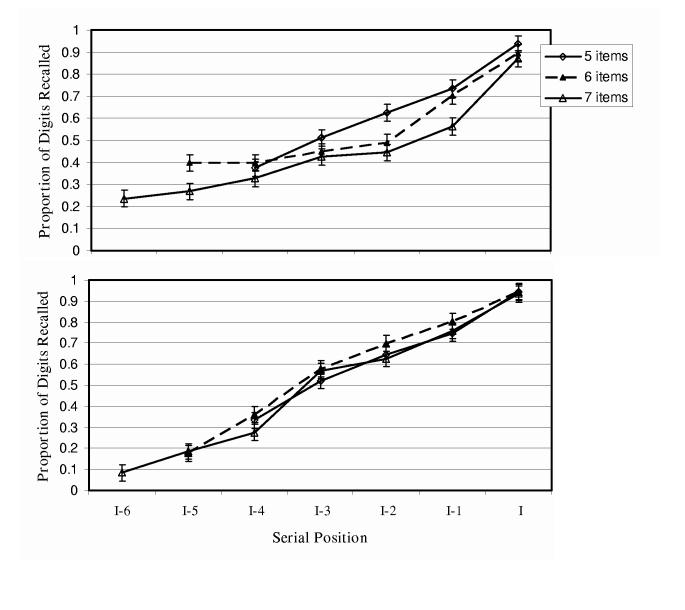
The results were clear. When a fixed number of digits had to be recalled (Figure 3, top panel), accuracy on items at each serial position depended on the number of items to be recalled. However, when the participant was free to recall only remembered items up to the number of spaces provided (Figure 3, bottom panel), recall depended only on serial position. This latter pattern is the one shown in Figure 1 as indicating only input interference, with no output interference.

Figure 3.

Proportion correct with a fixed recall window (top) and with a participant-determined recall window (bottom). Error bars represent 95% within-subject confidence intervals (Loftus & Masson, 1994).

The pattern was verified with an ANOVA of the last 5 serial positions in lists of every length in both procedures. Participants did better in the procedure in which they determined how many digits to recall (M = .65) than when the number of digits to recall was fixed (M = .58), F(1, 65) = 31.68, p <.001, η_p² = 0.33. Thus, having to guess at early digits interfered with memory for later digits.

Other theoretically meaningful effects include an interaction of Procedure x List Length, F(2, 130) = 9.41, p < .001, η_p² = 0.13,and Procedure x List Length x Serial Position, F(8, 520) = 4.81, p < .001, η_p² =0.07. With a fixed procedure, accuracy for the recall of 5, 6, and 7 digits was 0.64, 0.59, and 0.53, respectively, all significantly different by Newman-Keuls tests. Figure 3 (top) shows that the effect was largest at intermediate serial positions. When participants determined the number of digits to recall, the accuracy of recall of digits given 5, 6, and 7 answer spaces was similar: 0.64, 0.68, and 0.63. Although 6-space performance significantly exceeded the others, this does not conform to expectations based on output interference. In sum, output interference resulted primarily from having to guess earlier items, and was almost non-existent in the participant-determined procedure (Figure 3).

GENERAL DISCUSSION

Running memory span (Pollack et al., 1959) is a versatile procedure that is arguably simpler than fixed-length serial recall. Because running span does not produce a primacy effect, theoretical accounts of performance can focus on explanations of its recency effect. Performance processes still, however, can range from on-line rehearsal and updating (Postle, 2003) to retrieval from passive storage at the time of recall (Cowan et al., 2005). The present work shows that there is a place for both of these mechanisms.

In Experiment 1, performance was significantly higher with a slower-paced (1 s/item) than with a fast-paced (0.25 s/item) presentation, demonstrating the value of rehearsal in line with the analysis of Hockey (1973). Rehearsal seemed to act by diminishing input interference, reducing the loss of information over serial positions and thus making the serial position functions shallower (cf. Figures 1 & 2).

With either fast or slow pacing in Experiment 1, there was evidence of a similar amount of output interference (again, cf. Figures 1 & 2). In particular, recall accuracy at each serial position depended on how many other serial positions had to be recalled first. In Experiment 2, the reason for this output interference was identified. It occurred when a fixed number of digits had to be recalled (Figure 3, top panel), but disappeared when the participant was free to choose how many digits to recall (Figure 3, bottom panel). In the latter procedure, performance depended almost entirely on input serial position. This participant-determined recall procedure is therefore recommended as a way to elicit optimal performance and measure capacity. Indeed, Cowan et al. (2005) found that this participant-determined procedure yielded higher correlations with intellectual aptitudes in children and adults than did the other procedure.

Cowan (2001) suggested that there is a form of storage typically including 3 to 5 separate chunks of information in normal adults, and proposed that the special form of storage limit may be the capacity of the focus of attention (or scope of attention). The number of items that can be recalled in running span with fast presentation and a participant-determined recall set size may be equivalent to the scope of attention. A slow presentation appears to allow working-memory updating and rehearsal processes that, despite the difficulty of the task, raise performance levels somewhat beyond the scope of attention.