Swimming Paramecium in magnetically simulated enhanced, reduced, and inverted gravity environments

Abstract

Earth's gravity exerts relatively weak forces in the range of 10–100 pN directly on cells in biological systems. Nevertheless, it biases the orientation of swimming unicellular organisms, alters bone cell differentiation, and modifies gene expression in renal cells. A number of methods of simulating different strength gravity environments, such as centrifugation, have been applied for researching the underlying mechanisms. Here, we demonstrate a magnetic force-based technique that is unique in its capability to enhance, reduce, and even invert the effective buoyancy of cells and thus simulate hypergravity, hypogravity, and inverted gravity environments. We apply it to Paramecium caudatum, a single-cell protozoan that varies its swimming propulsion depending on its orientation with respect to gravity, g. In these simulated gravities, denoted by f_gm, Paramecium exhibits a linear response up to f_gm = 5 g, modifying its swimming as it would in the hypergravity of a centrifuge. Moreover, experiments from f_gm = 0 to −5 g show that the response is symmetric, implying that the regulation of the swimming speed is primarily related to the buoyancy of the cell. The response becomes nonlinear for f_gm >5 g. At f_gm = 10 g, many paramecia “stall” (i.e., swim in place against the force), exerting a maximum propulsion force estimated to be 0.7 nN. These findings establish a general technique for applying continuously variable forces to cells or cell populations suitable for exploring their force transduction mechanisms.

Swimming unicellular microorganisms such as bacteria and protozoa exhibit a variety of kinetic responses to external fields. Kinesis refers to a change in an organism's swimming speed or direction when exposed to external stimuli such as a chemical gradient (1), temperature gradient (2), and light (3). Of interest here is the gravikinesis exhibited by protozoa such as Paramecium, Didinium, and Loxodes (4–6). They actively alter their swimming speed as their orientation changes relative to Earth's gravity vector. This response enables them to fight sedimentation as they seek more favorable habitats (7). It is remarkable because it requires the ability to sense forces on the order of their apparent weight, which for Paramecium is only on the order of 100 pN. The details of how cells sense these small forces have not been established (8, 9).

Increasing the effective gravitational force accentuates graviresponses that are sometimes screened by other factors at normal gravity and thus difficult to detect (10, 11). Therefore, centrifugation simulations of increased gravity are attractive for studies of the gravisensitivies of swimming organisms (4, 5, 11), plant growth (12), and cell culture systems (13). Here, we will show that magnetic forces can be used to simulate variable gravity environments for paramecia. This work builds on previous studies using magnetic levitation (14–16) to simulate zero gravity for protein crystallization (17, 18) and fluid dynamics experiments (19) and magnetic forces to alter gravitropism in plants (20). In an earlier report (21), a magnetic force buoyancy variation technique (MFBV) was introduced to vary the apparent weight of immobile cells with magnetic forces. Here, MFBV is applied, with some modifications, to swimming paramecia to investigate their gravikinetic response. The advantage of MFBV as a gravity simulation technique is that it can simulate enhanced, reduced, and inverted gravities. Apart from centrifugation experiments in space, it is the only available method that can simulate both hypergravity and hypogravity in a single experimental setup. This quality permits direct comparative studies of the effects of these conditions on individual cell samples.

Our experiments show that paramecia exhibit a similar “negative” response to this magnetically simulated gravity environment as they do in centrifugation experiments. Their self-propulsion is greater when swimming against the simulated gravity force than when swimming with it. The gravikinetic response is linear from simulated −5 to 5 g and becomes nonlinear at higher simulated gravities. The gravikinetic factor obtained for the linear regime agrees with previous centrifugation results (4, 5). When the simulated gravity approaches 10 g, most paramecia orient antiparallel to the force direction and on average propel without advancing, i.e., they stall. This behavior suggests a maximum propulsive force for Paramecium of ≈0.7 nN.

Experimental Procedures

The gravity simulation method is based on the magneto-Archimedes principle, which has been used to “float” gold and other relatively dense diamagnetic materials (22, 23) and cells (21, 24) in solutions of lesser density. When a cell in solution is placed in an inhomogeneous magnetic field, B(z), the magnetic force changes the buoyancy or the apparent weight per volume from w_g = Δρg to w_gm = Δρg − ΔχBB′/μ₀, where B′ is the derivative of B(z) with respect to the vertical direction z. Δρ = ρ_cell − ρ_sol and Δχ = χ_cell − χ_sol represent the differences between the cell and solution densities and magnetic susceptibilities, respectively, and μ₀ = 4π × 10⁻⁷ H·m⁻¹ is the permeability of free space. It is important to note that in this approach we consider the cell as homogenous and thus χ_cell and ρ_cell are the average values for the whole cell. For simplicity, we define the net force per mass, f_gm, as:

Similar to a centrifuge, f_gm can be increased continuously. Moreover, simulated zero gravity, f_gm = 0, or decreased/inverted gravity, f_gm < g, also can be attained.

According to Eq. 1, the magnitude and the direction of f_gm can be tuned by changing either or all of Δχ, Δρ, and BB′. In our experiments, Δρ was held fixed at its natural value, which is Δρ = 40 kg·m⁻³. For Paramecium in water, χ_sol = −0.904 × 10⁻⁵ and χ_cell = −0.911 × 10⁻⁵ (21) so that Δχ = −0.007 × 10⁻⁵ (Système International, SI). This value affords a maximum adjustment of f_gm of only ≈50%, with the available BB′. Alternatively, a larger range of f_gm was produced by doping the solution with a fixed concentration of the paramagnetic compound gadolinium-diethylene-triamine-pentaacetate (Gd-DTPA) (see Materials and Methods) to enhance |Δχ|. A 4-mM solution of Gd-DTPA has a susceptibility, χ_sol (4 mM) = −0.764 × 10⁻⁵ (SI) estimated from χ_Gd-DTPA = 0.028 cm³·mol⁻¹ (24). The addition of Gd-DTPA also increases χ_cell because paramecia exchange solution constantly. However, χ_cell changes by a smaller amount than χ_sol, leading to a net increase in Δχ. The value of Δχ was determined experimentally for each solution by measuring the BB′ at which immobilized paramecia were neutrally buoyant, i.e., f_gm = 0:

For 4 mM Gd-DTPA, (BB′)₀ = −510 ± 10 T²·m⁻¹, implying Δχ = −(0.097 ± 0.002) × 10⁻⁵ (SI), and for 2 mM Gd-DTPA, (BB′)₀ = −1,020 ± 20 T²·m⁻¹, implying Δχ = −(0.048 ± 0.002) × 10⁻⁵ (SI).

For each sample of swimming paramecia, f_gm was adjusted by varying BB′ at fixed Gd-DTPA concentration and calculated by using a rewritten version of Eq. 1:

Thus, varying BB′ over the maximum range available yields −8 g ≤ f_gm ≤ 10 g and −3 g ≤ f_gm ≤ 5 g for the 4-mM and the 2-mM Gd-DTPA concentrations, respectively.

Results and Discussion

Samples of the swimming tracks of paramecia in f_gm = 4, 0, and −4 g are shown in Fig. 1. These and virtually all of the tracks can be labeled as either upward (green) or downward (red) because of a helpful artifact of this magnetic gravity simulation method. Magnetic fields align the trajectories of swimming paramecia parallel to the field lines without influencing their swimming speed (25). In our setup, where the magnetic field is parallel to the simulated gravity vector, the fraction of vertical swimmers within 10° of vertical approaches 100% for B > 10 T. This artifact ameliorates the quality of the statistical analysis.

Fig. 1.

The swimming trajectories and speed distributions of paramecia in variable simulated gravity. (a–c) f_gm is −4 g (a), 0 g (b), and 4 g (c). Upward (green) and downward (red) swimming trajectories were each tracked for 3 s in simulated gravity. (Scale bar: 500 μm.) (d–f) The upward and downward swimming speed distributions at each f_gm. The bulleted line shows the mean velocity. The bin size is the SD of speed distribution in each direction. Notice that virtually all of the tracks are upward or downward because of magnetic field alignment (see Results and Discussion).

Inspection of the swimming tracks reveals that paramecia swim faster downward (Fig. 1, red) than upward (Fig. 1, green) in f_gm = 4 g and vice versa in f_gm = −4 g. At f_gm = 0 g the upward and downward rates are comparable. The histograms in Fig. 1 show the corresponding velocity distributions (the bin size is 1 SD). Eighty percent of all of the distributions were normal to a 95% confidence level as determined by the Lilliefors test. Moreover, for all distributions, the maximum variation between the mean and the median of the velocities was 3%, which justifies the use of the mean rather than the median velocity in our analysis. Evaluation of a few hundred tracks at each f_gm shows that the mean speeds of vertical upward, V_U, and downward, V_D, swimmers decrease and increase, respectively, nearly linearly with f_gm from −5 to 5 g as shown in Fig. 2a. Note that “up” and “down” are relative to Earth's gravity vector and therefore for f_gm > 0 up signifies swimming against the force, whereas for f_gm < 0 up signifies swimming with the force.

Fig. 2.

Swimming speed of Paramecium in simulated gravity. (a) Mean upward (▴) and downward (▾) swimming speeds as a function of simulated gravity for trial 1. The bars indicate the widths of the speed distributions. The upper bar represents the first 68% of swimmers above the mean, and the lower bar indicates the first 68% of the swimmers below the mean. The solid lines denote the predicted change in the swimming speed in the absence of any kinetic effects. Their widths indicate the uncertainty in the mean sedimentation rate. (b) Linear fits to up and down swimming speeds. α and β are the fitting parameter to the line V = αf_gm/g + β. Data at f_gm = 0 are eliminated to reduce fitting error. Note that inverting the simulated gravity inverts the effect.

To assess whether the variation of V_U(f_gm) and V_D(f_gm) involves an active kinetic response to this magnetically generated force, it is necessary to first account for their passive tendency to sediment. Sedimentation is expected to lead to a linear dependence of V_U(f_gm) and V_D(f_gm) on f_gm as given by:

where V₀ denotes the average swimming speed at f_gm = 0 and v_S is the sedimentation rate at 1 g (4). We measured v_S by first levitating immobilized cells in a 4-mM Gd-DTPA solution and then releasing them to sediment by turning off the magnetic field. Measurements on 120 cells yielded v_S = 97 ± 2 μm·s⁻¹ (mean ± SE, σ_S = 22 μm·s⁻¹) similar to previously reported values (6).

The two solid lines in Fig. 2a represent the passive model embodied in Eq. 4. The uncertainty in the sedimentation speeds is indicated by the thickness of each line in Fig. 2a. V₀ was estimated from the weighted average of the y-axis intercepts of the linear fits to the data (Fig. 2b). The tendency to sediment without active regulation leads to a difference between downward and upward swimming rates given by:

which corresponds to the vertical separation of the solid lines in Fig. 2a. The measured V_U(f_gm) and V_D(f_gm), however, fall within the envelope defined by these lines, indicating that paramecia exhibit a negative kinetic response to f_gm.

To analyze this response, we use the terminology of Machemer and Braucker (6), decomposing the speed in each direction as:

Here, Δ_U(f_gm) and Δ_D(f_gm) are the gravikinetic factors for up or down swimmers, respectively. The average gravikinetic factor, Δ(f_gm) = [Δ_D(f_gm) + Δ_U(f_gm)]/2 readily follows as:

The measured Δ values as a function of f_gm for three different trials are plotted in Fig. 3. Each follows a linear dependence, Δ(f_gm) = Δ′f_gm/g + Δ₀ for the −5 g ≤ f_gm ≤ 5 g regime with similar slopes, Δ′. The specifics of each trial are summarized in Table 1. The average value of Δ′ from the three trials, 〈Δ′〉 = −50 ± 1 μm·s⁻¹, agrees with that measured for paramecia in the hypergravity of centrifuges (4–6, 26). Δ₀ exhibits a small variation of unknown origin from experiment to experiment. We cannot discern whether it is zero.

Fig. 3.

Gravikinetic factor measured for the three trials introduced in Table 1. The lines are least-square fits to the data. The negative slope implies negative gravikinesis. The fit parameters are given in Table 1. The uncertainty bars are ± 1 SD.

Table 1.

Gravikinetic factors, Δ, Δ₋, and Δ₊, for −5 g ≤ f_gm ≤ 5 g from three trials

Trial	Gd-DTPA	Δ = Δ′ fgm/g + Δ0, μm·s−1		V0, μm·s−1	Δ− = Δ−′fgm/g+Δ−0, μm·s−1		Δ+ = Δ+′fgm/g + Δ+0, μm·s−1
		Δ′	Δ0		Δ−′	Δ−0	Δ+′	Δ+0
1	4 mM	−53 ± 1	15 ± 2	450 ± 25	−63 ± 5	12 ± 15	−46 ± 2	4 ± 6
2	4 mM	−57 ± 1	3 ± 4	400 ± 30	−66 ± 2	3 ± 7	−48 ± 1	2 ± 3
3	2 mM	−49 ± 1	17 ± 3	510 ± 25	−65 ± 1	17 ± 3	−32 ± 2	19 ± 5

The slopes of fitted lines to up and down swimming speeds in Fig. 2b differ, suggesting that the regulation depends on whether the paramecia are swimming with or against the force. To quantify these phenomena, we define Δ₊(f_gm) and Δ₋(f_gm) to be the kinetic factors for swimming with or opposed to the applied force, respectively. For f_gm > 0, Δ₊(f_gm) = Δ_D(f_gm) and Δ₋(f_gm) = Δ_U(f_gm) and vice versa for f_gm < 0 g (Eq. 6). The measured values for Δ₊(f_gm) and Δ₋(f_gm) for the three trials are summarized in Table 1. Even though exact measurements of Δ₊(f_gm) and Δ₋(f_gm) are difficult because of uncertainties in estimating V_S(f_gm) and V₀, there are common trends in all trials. The regulation for both up and down swimmers increases with f_gm. In all cases paramecia swimming against the force adjust more than those swimming with the force as found by comparing the slopes of linear fits to Δ₊(f_gm) and Δ₋(f_gm) (Δ₊′ and Δ₋′, respectively) (see Table 1). This latter finding agrees with previous experiments based on centrifugation (4, 5, 26).

At high f_gm, nonlinearities in the response become evident, as shown in Fig. 4a. V_U(f_gm) appears to saturate at a minimum speed of ≈220 μm·s⁻¹ for 5 g < f_gm < 10 g. V_D(f_gm) also saturates in this regime but less prominently. In both cases these behaviors are consistent with an enhanced negative gravikinetic response in the high f_gm regime. It is possible to extract the average propulsion force exerted by the paramecia and measure directly their active fight against sedimentation. Their propulsion force, F_P(f_gm), is balanced by the sum of their apparent weight and the drag force exerted on them by the solution.

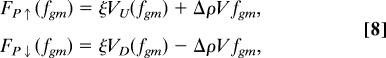where ξ is the linear drag coefficient. We estimated ξ and V by modeling the paramecia as solid ellipsoids of revolution with semiminor and semimajor axes of a = 20 ± 5 μm and b = 100 ± 10 μm, respectively. In this approximation ξ = 6πη(4a + b)/5 (27), where η is the viscosity of the medium; in our experiments η = η_water = 10⁻³ Pa·s. The resulting F_P↑ (up) and F_P↓ (down) are shown in Fig. 4b. Up to f_gm = 5 g, they appear linear in f_gm. Above f_gm = 5 g, F_P↑ rises more rapidly and F_P↓ decreases more rapidly consistent with the nonlinearity in Fig. 4a. At the highest f_gm, both the downward and upward swimmers reach their capacity for adjusting their forward propulsion force. Near f_gm = 8 g, F_P↓ → 0, suggesting the paramecia stop swimming. It is not clear whether they cease to beat their cilia entirely or adjust the angle of their ciliary beating so that they exert no forward propulsion force. Detailed investigations of individual swimmers may discern which possibility is correct. Whichever the case, their behavior is consistent with free sedimentation.

Fig. 4.

Gravikinesis in the high f_gm regime. (a) The swimming speed response becomes nonlinear for f_gm > 5 g. At 10 g, upward swimming paramecia stop advancing. No downward swimmers were observed. (b) Mean propulsion force, F_P, for up and down swimmers given by: F_P↑ (f_gm) = ξV_U(f_gm) + ΔρV f_gm, and F_↓ (f_gm) = ξV_D(f_gm) − ΔρV f_gm, respectively. At f_gm = 10 g, F_P↑ is estimated from stalled paramecia. The bars indicate the range of propulsion forces exhibited by the 68% of the swimmers nearest the mean. (c) Vertical position of upward oriented paramecia at f_gm = 10 g as a function of time. Arrows show points where paramecia stop propelling and drop at a rate consistent with free sedimentation at f_gm = 10 g. The movies for this experiment were digitized at 10 fps.

Above f_gm = 8 g, a number of downward swimmers were observed to flip midtrajectory to orient anterior end up and swim against the force. The upward swimmers approach their maximum propulsion force, 0.7 nN, at f_gm = 8 g. At even higher f_gm, f_gm ≈ 10 g, the upward oriented cells tend to stall (i.e., V_U ≃ 0) as shown by the plot of the vertical position as a function of time for a number of paramecia (Fig. 4c). They move slowly forward or backward at a body length per s or less before stalling in a new position. Occasionally a Paramecium drops abruptly. These events are indicated by the arrows in Fig. 4c. Analysis of 30 tracks shows that these drops occur at a rate of 1,044 ± 225 μm·s⁻¹ (mean ± SD), which is close to the estimated passive sedimentation speed at f_gm = 10 g. Our measured stalling force, F_Pmax = ΔρV f_gm = 0.7 nN, is ≈10 times smaller than that reported by Kuroda and Kamiya (28) using density graded solutions and a high-speed centrifuge.

The distribution widths in Fig. 1, and correspondingly the length of the bars in Fig. 2a, show an interesting trend with f_gm. At f_gm = 0 g, the widths defined as σ of both the upward and downward swimming speed distributions are almost equal. Moving to nonzero f_gm, the distributions narrow (broaden) for the swimmers moving against (with) the force. We can explain this behavior by considering the factors that contribute to σ and depend on f_gm. According to Eq. 6 the swimming speed of a Paramecium at a given f_gm is the sum of its zero gravity propulsion, V₀, sedimentation, V_S(f_gm), and gravikinetic response, Δ_i(f_gm) (where i denotes up or down). These parameters each have a corresponding distribution width of σ₀, σ_S, and σ_Δi, respectively. Generally, the total width, σ_i, of the speed distribution can be written as:

The cross terms are given for example by:

(29), where the subscript j denotes the value for each individual, and N is the total number of paramecia. V̄_S, V̄₀, and Δ̄_i represent the mean values of the distributions.

In the absence of correlations, the cross terms in Eq. 9 are zero, and hence we might expect σ_i to only increase with |f_gm|, because V_S(f_gm) and Δ_i(f_gm) are proportional to |f_gm| and therefore σ_S and σ_Δi are also linear functions of |f_gm|. Note that σ₀ does not depend on |f_gm|. Thus, to account for the near independence of σ_i on |f_gm| for paramecia swimming against the force, we need to consider the correlation terms. These can be negative, which will tend to reduce the total width. As a plausible example, consider that both propulsion and sedimentation depend on the drag coefficient. Paramecia that propel faster are likely to sediment faster as well. Consequently, this correlation leads to σ_0,S > 0. For swimmers with the force,

because the sedimentation and propulsion velocities point in the same direction. Therefore σ_i increases with f_gm. Conversely, σ_i has a tendency to decrease for swimmers against the force because the sedimentation and propulsion velocities point in opposite directions, resulting in

That is, sedimentation pulls the faster swimmers back into the pack.

As shown in Fig. 2, magnetic forces can be used to vary the buoyancy of the cells in solutions similar to density variation methods. Moreover, one can invert the direction of total buoyancy. This quality can be helpful for determining whether paramecia use a gravisensing mechanism similar to Loxodes (30). Loxodes have organelles, called Müller bodies, containing BaSO₄ grains that are attached to the cell membrane by filaments. In a gravitational field, the displacement of these dense bodies with respect to the cell acts as the gravisensor (30). The action of this sensor does not depend on the density of the surrounding solution (31). Correspondingly, neutrally buoyant Loxodes still sense gravity. The graviresponse of Paramecium, on the other hand, tends to disappear when it is made neutrally buoyant by matching the density of the solution with the addition of Ficoll or Percoll (4, 31, 32). The symmetry of the graviresponse in Fig. 2 (i.e., inverting the buoyant force inverts their graviresponse) suggests that paramecia either do not have internal gravisensing organelles, or the properties of the organelles are such that their buoyancy within the cytoplasm varies with BB′ in the same way as the buoyancy of the cell in solution. We investigate the latter possibility for organelles containing BaSO₄ particles for which ρ_org = 4,500 kg·m⁻³ and χ_org = −1.8 × 10⁻⁵ (SI). The BB′ required to make such particles neutrally buoyant within the cytoplasm is estimated from Eq. 2 by replacing Δρ and Δχ by Δρ′ = ρ_org − ρ_cyt and Δχ′ = χ_org − χ_cyt; the subscripts “org” and “cyt” denote the organelle and the cytoplasm, respectively. Approximating χ_cyt ≃ χ_cell and ρ_cyt ≃ ρ_cell, we obtain that (BB′)_0,org = 4,500 T²·m⁻¹, which is much larger than (BB′)₀ for a Paramecium in a 4-mM Gd-DTPA solution. Moreover, even if these (BB′)₀s were to match for 4-mM Gd-DTPA solutions, it seems highly unlikely that they would match for a different Gd-DTPA concentration. Thus, the data in Fig. 3 also tend to rule out the possibility of an internal gravisensor. The possibility remains that the whole cell acts as a statocyte (4, 26) although the forces exerted by the cytoplasm on the membrane are extremely small. Alternatively, the cells may use an indirect mechanism to sense gravity (33). The details by which such cells sense the gravitational field remain to be determined.

Conclusion

We have demonstrated that simulations of increased and decreased gravities ranging from −8 to 10 g using magnetic forces can elicit a biological response. This gravity simulation technique provides an alternative to currently used “microgravity” simulation techniques such as the rotating wall vessel (RWV) suspension technique. For example, it can also be used for investigations of 3D tissue engineering (34, 35) and microgravity-induced changes in osteoblast growth (36), gene expression (37), skeletal muscle adaptation (38), and cell signaling (39) without the shear stress associated with the RWV. More generally, this noninvasive technique can be used to apply forces to the whole bodies of populations of cells, and thus, can serve as an alternative to “point-like” methods like atomic force microscopy (40) and magnetic tweezers (41) that apply local stresses to single cells.

Materials and Methods

Paramecium and Gd-DTPA Solution.

P. caudatum (Carolina Biological Supply, Burlington, NC) was cultured on Hey medium inoculated by Enterobacter aerogenes. At their stationary phase of growth, they were collected by using low-speed centrifugation and suspended in test solution containing 1 mM CaCl₂, 1 mM KCl, 0.1 mM MgSO₄, and 1.5 mM Mops at pH 7.2. The paramecia were left in this solution for up to 2 h to adapt before experimentation.

To enhance the magnetic properties of the aqueous solution Gd-DTPA (Sigma-Aldrich, St. Louis, MO), a paramagnetic MRI contrast-enhancing agent (24, 41) was added to the test solution in 2 and 4 mM concentrations (pH 7.2). Gd-DTPA was chosen because it provides the strong paramagnetic response of Gd without producing a high concentration of Gd³⁺ ions as a salt like GdCl₃ would. Free Gd³⁺ ions are known as a Ca²⁺ inhibitor, which can affect ciliary motion (42). At these low concentrations of Gd-DTPA, paramecia showed no behavioral changes such as a change in swimming pattern and could survive for a few days. We did observe, however, that the swimming speed of paramecia dropped uniformly in Gd-DTPA solutions. No direct relationship between the Gd-DTPA concentration and speed could be deduced. Gd-DTPA's role in reducing the swimming speed of paramecia remains to be investigated.

Paramecia were immobilized by suspension in 0.5 mM NiCl₂ for 10 min. The NiCl₂ solution was made such that the final solution had the desired concentration of Gd-DTPA (2 or 4 mM) by diluting high concentration of NiCl₂ with solution containing Paramecium and high concentration of Gd-DTPA. After the paramecia were immobilized, they were collected with a micropipette and transferred into the experimental chamber containing the same concentration of Gd-DTPA (2 or 4 mM).

The experiments were performed in two types of chambers. Both types had a depth much smaller than the width and length to provide a nearly 2D environment. The square chambers (trial 3) were made of an acrylic frame of 2-mm depth and 15 × 15-mm² area. Both sides of the frame were covered with microscope slides and sealed with 5-min epoxy (Devcon, Glenview, IL). The chambers were flushed a few times with water and tested to be harmless to paramecia. Solution containing paramecia were injected with a syringe through holes on one side of the frame. These holes were later sealed with VALAP (1:1:1 vaseline/lanolin/paraffin). The second type of chamber had a rectangular geometry (trials 1 and 2). These were made from borosilicate rectangular tubes of dimensions 2 × 4 × 10 mm³ (VitroCom, Mountain Lakes, NJ) whose ends were sealed with acrylic caps.

Apparatus.

The experiments were carried out by using a resistive magnet at the National High Magnetic Field Laboratory (Tallahassee, FL). The magnet has a 50-mm bore and produces a 31-T maximum field and 4,754 ± 170 T²·m⁻¹ maximum BB′. The motion of paramecia was observed by using a 6-mm 90° side-view borescope (ITI, Westfield, MA), which provided an optical axis perpendicular to the magnetic field. The temperature of the chambers containing paramecia was kept at 22°C by using a water-circulating bath. Their motions were imaged with a CCD camera (XC-333, Sony, Tokyo, Japan) and recorded with a videocassette recorder. Green light generated by a light-emitting diode (565 nm, Luxeon V star LED, Lumileds Lighting, San Jose, CA) was used for illumination. A frame grabber (EPIX, Buffalo Grove, IL) digitized the movies at five frames per s for 3–4 min. Associated software (XCAP, EPIX) was used to generate the trajectories of swimming paramecia from the digitized movies. Further analysis was done by using custom-made Matlab (Mathworks, Natick, MA) codes. Details are explained elsewhere (43).

Reduced and inverted simulated gravity, f_gm < g, experiments were performed by placing the experimental chamber above magnet center where BB′ < 0 and for increased simulated gravity, f_gm > g, the chamber was placed below the center of the magnet where BB′ > 0. The control experiments, f_gm = g, were carried out at the center of the magnet where BB′ = 0. At all positions B and B′ were varied by adjusting the magnet current.

The velocity of a Paramecium was calculated as the displacement vector of the total trajectory divided by total time. Only trajectories that extended a couple of spatial periods or more and had an inclination angle of a maximum of 10° from the vertical were analyzed. The latter constraint insured that only vertical trajectories were analyzed. To minimize the influence of hydrodynamic interactions with the walls, only tracks that were at least a few body lengths away from the walls were analyzed. Because some paramecia reverse their swimming direction or make abrupt turns because of avoiding reactions such as bumping into other paramecia or particles in water, a filtering procedure was used to eliminate those tracks from final analysis.

Abbreviations

SI

Système International

Gd-DTPA

gadolinium-diethylene-triamine-pentaacetate