Scale-invariant structure of strongly conserved sequence in genomic intersections and alignments

Abstract

A power-law distribution of the length of perfectly conserved sequence from mouse/human whole-genome intersection and alignment is exhibited. Spatial correlations of these elements within the mouse genome are studied. It is argued that these power-law distributions and correlations are comprised in part by functional noncoding sequence and ought to be accounted for in estimating the statistical significance of apparent sequence conservation. These inter-genomic correlations of conservation are placed in the context of previously observed intra-genomic correlations, and their possible origins and consequences are discussed.

Selection and neutral drift, the dynamic duo of evolution, lead to degradation or loss of nonfunctional genomic sequence. Sequences greater than 50 nt in length (L) perfectly conserved among sets of diverse genomes (ultraconserved elements, or UCEs) have only recently been identified in mammals; they are enriched for and cluster near known functional elements (1–3). For example, ultraconserved elements with L > 100 shared by human, mouse, and rat genomes that overlap exons are enriched in genes for RNA binding, DNA binding, and transcriptional regulation; those that do not overlap exons tend to cluster near regulatory genes and sequences (1). Microconserved elements (perfectly conserved sequences with L < 50) are strongly enriched for mature micro-RNAs, other noncoding RNAs, and transcription factor binding sites (4) (T. Tran, P.H., and J.M., unpublished data).

In this article, we examine the length and spatial distributions of sequences perfectly conserved between the mouse and human genomes. Whereas for the most part we study “maximal L-mers” (sequences common to multiple genomes that are not contained in any longer sequences common to those genomes), mouse and human are sufficiently closely related that for L >30, this set is nearly identical to perfectly conserved sequences obtained from whole-genome alignment, differing in total number at L = 40, for example, by <3%.

Results

Distribution of Maximal L-mer Lengths in a Mouse/Human Genome Intersection.

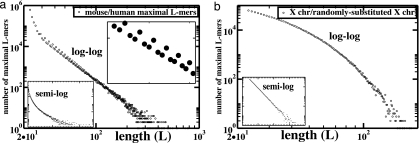
We identified nearly 1.6 × 10⁶ distinct maximal L-mers with L ≥ 23 common to repeat-masked mouse and human genomes, a set of sequences that we refer to as a “genomic intersection.” Their lengths are displayed in Fig. 1a on a log–log scale and in the Inset on a semilogarithmic scale. The linear regime on the log–log scale starting at L ∼ 30 encompasses just under 2.7 × 10⁵ sequences covering 1.3 × 10⁷ bases, or ≈0.9%, of the repeat-masked mouse genome (for rat/mouse intersections, this figure is closer to 10%). As a comparison, we randomly mutated repeat-masked mouse X chromosome at a rate of 0.1 substitutions per base and intersected it with the unmutated mouse X chromosome; Fig. 1b shows the anticipated exponential (or geometric) maximal L-mer length distribution—a convex curve on the log–log plot and a straight line on the semilogarithmic Inset. The 3-fold modulation of the mouse/human L-mer distribution at small L (Fig. 1a Inset) can be averaged over nearest neighbors (Fig. 2, curve d) to more clearly exhibit the linearity of this distribution on a log–log plot, revealing a power-law (or algebraic) distribution over more than four orders of magnitude in the ordinate, with a power close to −4. This observation seems to rule out a uniform rate of spatially uncorrelated base substitution, a standard “null-model” for estimating significance of sequence conservation.

Fig. 1.

Distributions of perfectly conserved sequence lengths in genomic intersections. (a) Log–log plot of the number of distinct maximal L-mers from mouse/human whole-genome intersection. The Inset at the lower left shows the same data on a semilogarithmic scale. The Inset at the upper right expands the small-L regime to show the 3-fold modulation clearly. (b) Log–log plot of the intersection of mouse X chromosome with a version of itself that has been randomly mutated at a rate of 0.1 substitutions per base.

Fig. 2.

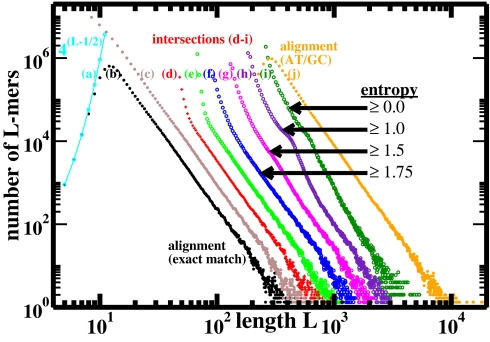
Length distributions (three-point running averages) of perfectly conserved L-mers from mouse/human genome alignment and intersection. Curve a, maximum possible number of distinct mers of length L (cyan); curve b, whole-genome alignment from UCSC, for L ≥ 4 (hg17/mm6): distinct sequences (black); curve c, same whole-genome alignment: all sequences (brown); curve d, intersection of repeat-masked genomes (red). No RepeatMasker: curve e, distinct maximal L-mers in intersection containing no 23-mer subsequence that occurs more than once in either genome (green); curves f–i, single-copy maximal L-mers in intersection with entropy of base composition exceeding selected values in bits (blue, magenta, violet, and dark green); curve j, (repeat-masked) whole-genome alignment as in curve b, allowing A/T and G/C substitutions within an L-mer (orange). Except for curve a, distributions are offset in the horizontal direction from the whole-genome alignment (curve b) for clarity of presentation; otherwise the linear regimes of curves b–f would fall right on top of one another.

The power-law distribution is readily apparent in intersections of orthologous fragments of sequence as short as 4 Mb (see Fig. 6, which is published as supporting information on the PNAS web site). Furthermore, the distribution of perfectly conserved sequence lengths derived from human/mouse whole-genome alignment [ultraconserved elements for L ≥ 50 (1)] exhibits the same power law (Fig. 2, curves b and c), extending from lengths as short as 12 bases through nearly six orders of magnitude in number; when A/T and G/C substitutions are permitted, the power is slightly altered (Fig. 2, curve j).

Repeat-Masking.

In the computations described so far, both mouse and human genomes were first “repeat-masked.” RepeatMasker (6) is a heuristic algorithm that identifies and tags (or “masks”) certain classes of sequence occurring throughout a genome as multiple repeats or near-repeats, based on a list of manually curated elements such as SINEs, LINEs, Alu, and satellite DNA; excessively “simple” sequences are tagged as well. Eukaryotic whole-genome alignments are ordinarily repeat-masked before alignment by, e.g., BLASTZ (7) or LAGAN (8); the masked sequence is later reinserted. In the neighborhood of half of a vertebrate genome may be masked. The original motivation for masking repeats here, as elsewhere, was the desire to avoid the capture of “simple” and/or complex repetitive interspersed sequences. Repetitive/simple sequence can be subject to distinctive evolutionary forces such as intrachromosomal recombination at frequencies beyond that of single-copy sequence (9). These forces may be reflected in the differences between curves f and i in Fig. 2, which are accounted for primarily by low-complexity sequences with Alu and interspersed repeats contributing significantly only for lengths ≤40.

To eliminate the possibility that the source of our observations is an artifact of the RepeatMasker algorithm, we examined intersections of mouse and human genome sequences that were not preprocessed by RepeatMasker but instead were subject to two different ad hoc but much simpler filters. Sets of single-copy sequence were generated from the genomic intersection in two distinct ways: (i) by discarding any maximal L-mer that contained as a subsequence a 23-mer that occurred more than once in either genome (Fig. 2, curve e); and (ii) by discarding any maximal L-mer that occurred more than once in either genome, and subsequently eliminating sequences whose entropy of base composition was less than a specified value (Fig. 2, curves f–i). Evidently, these two classes of complex, single-copy maximal L-mers exhibit the same power-law length distribution as the repeat-masked sequence (Fig. 2, curve d).

Spatial Correlations of Mouse/Human Maximal L-mers in the Mouse Genome.

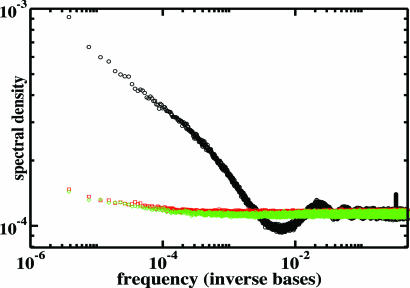
The power spectrum of mouse/human maximal L-mer positions within the mouse genome (red points in Fig. 3) exhibits several conspicuous features: (i) a peak at a wavelength corresponding to 3 bases—this mode has been observed in the power spectrum of single genomes and is also reflected in the maximal L-mer distribution; (ii) harmonics with a peak near 30 bases that arise because termini of two maximal L-mers of minimum length L can be no less than L + 1 bases apart (otherwise, their concatenation would have been recorded as a single maximal L-mer); and (iii) a linear regime, starting at a wavelength of 5,000 and extending to the window size (2¹⁸), reflecting power-law decay of maximal L-mer positional correlations within the mouse genome. The slope of this linear regime corresponds to an exponent of −3/4 for decay of correlations in real space.

Fig. 3.

Log–log plot of window-averaged power spectra for mouse/human maximal L-mer locations over the mouse genome and for random “control” sequences (see Repeat-Masking). Black, mouse/human maximal L-mers; red, random locations: excluded from masked regions of genome; green, minimally separated and excluded from masked regions. See Supporting Methods and Fig. 7b.

In this analysis, maximal L-mers are disjoint from repeat-masked sequence and the genome is effectively fragmented by repeat-masked intervals. The lengths of the remaining unmasked intervals themselves display a distribution that may contain a power-law regime (Fig. 7a, which is published as supporting information on the PNAS web site). To confirm that correlations seen in the mouse/human intersection power spectrum are not artifacts of this fragmentation, we constructed two random sequences that contained the same mean density of 1s as did the sequence derived above directly from the mouse/human maximal L-mer locations but subject to constraints of (i) exclusion from masked regions of the genome and (ii) minimum separation. The power spectra of the random signals show little modulation across all wavelengths (Fig. 3). These observations indicate that the power-law decay of maximal L-mer correlations is not an artifact of RepeatMasker, although we are not suggesting that repetitive sequence does not play a role in the evolutionary processes from which these correlations arise.

Spatial Clustering.

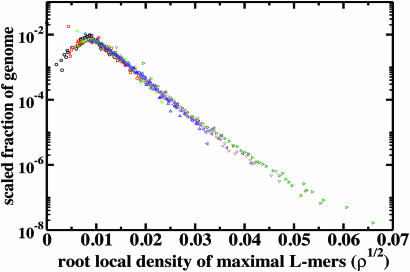
Ultraconserved elements have been observed to cluster in the neighborhood of functional genomic sequences (1). To quantify clustering, we computed the fraction, f, of mouse genome with a given local density of maximal L-mers, ρ. The local density ρ_n is defined as the number of maximal L-mers per base within a sequence window of length n. We divided the repeat-masked mouse genome into nonoverlapping windows of length n and computed the distribution of local densities for log₂n = 2, 3, …, 22. For n below the inverse mean density of L-mers (≈2¹¹ bases), trivial scaling is expected and observed, whereas for excessively large n, sampling issues dominate. In the intermediate regime, 14 ≤ log₂n ≤ 20, we find that we can collapse the curves onto one another as shown in Fig. 4, yielding a scaling function h(ρ) = f(ρ_n)/g_n, where ρ is independent of n, g_n is the multiplicative factor needed to collapse f(ρ_n), and h is evidently a stretched exponential, exp(−κρ^1/2); κ is a constant. Thus, the L-mers form denser clusters and sparser lacunae than randomly chosen positions, which exhibit a Gaussian scaling function. This observation can be summarized loosely as an “attraction” between maximal L-mers. A stretched-exponential for GC clustering was reported previously (10).

Fig. 4.

Scaling function h for the fraction f of repeat-masked mouse genome (y axis) with a given local density of maximal L-mers ρ (x axis). Note that a square-root has been taken on the x axis. A stretched exponential is observed, whereas a spatially random choice of positions in the repeat-masked mouse genome yields the expected Gaussian, with a quartic decay on this plot (data not shown). Window lengths are 2ⁿ for n = 14 (dark green), 15 (brown), 16 (violet), 17 (blue), 18 (green), 19 (red), and 20 (black).

Power-Law Distribution of “Highly Conserved” Sequence.

State-of-the-art methods used to estimate the significance of conserved sequence are described in two recent papers (11, 12). In ref. 11, highly conserved sequence within the aligned CFTR locus from 29 mammals was identified through phylogeny-based position-by-position computation of the ratio of observed to expected substitution rates (see Methods). The significance of conservation was assessed by comparing the total length of “highly conserved” sequence against the total length of sequence yielded by a “null model” in which the substitution rates were randomly permuted in space. The null model plays an essential role in their analysis by allegedly making it possible to identify regimes where conservation exceeds what would be expected under neutral drift alone.

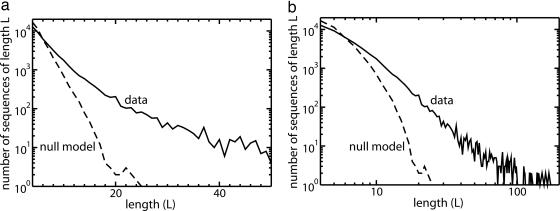
We analyzed the length distributions for the data and the null model, based on the sequences of expected/observed substitutions that were provided as supplementary data to ref. 11. As exhibited in Fig. 5, the lengths of “highly conserved” sequences display a power-law distribution, whereas for the null model the length distribution decays exponentially. The interpretation of “rejected substitutions” (RS) computed in ref. 11 relies on the independence of additive contributions, so that events arising from intragenomic correlations may be attributed to selection, leading to overestimates of the significance of longer sequences and underestimates of the significance of shorter sequences.

Fig. 5.

Length distribution of the highly conserved L-mers derived by Cooper et al. (11). (a) Semilogarithmic plot. (b) Log–log plot. Number of sequences as a function of length is plotted for the threshold RS value of 8.5 selected in ref. 11 but is very insensitive to the choice of this quantity. Dashed line, null model; solid line, alignments of CFTR loci. The horizontal scale of the semilogarithmic plot is expanded to exhibit the linearity of the null model curve on these axes.

The critical distinction is drawn in ref. 11 between substitutions arising from neutral drift versus those arising from selection and is accounted for by the RS. The same distinction applies to correlations; that is, one would expect to find intragenomic positional correlations of observed substitution rates that differ from those of expected substitutions; however, to recover an uncorrelated RS would require some kind of cancellation between the long-range components of these two contributions, which seems to us implausible.

As reviewed in Discussion, slowly decaying positional correlations are a well known phenomenon in noncoding sequence and can arise in the absence of selection. We would expect the method of ref. 11 to be applicable in the study of protein-coding exonic sequence where exponentially decaying correlations appear to be typical; but in general, their null model seems to be difficult to justify and sheds some doubt on the proper interpretation of their calculations.

The methodology of ref. 12 is explicitly biased in favor of coding exons, which are known to display exponentially decaying spatial correlations, and their null model neglects correlations in the same spirit as ref. 11; they report a geometric (exponential) distribution of highly conserved sequence lengths. Our human/dog/frog whole-genome intersections (T. Tran, P.H., and J.M., unpublished data) exhibit a power law and show >10³-fold enrichment for certain classes of functional noncoding elements but are close to neutral with respect to coding exons.

Discussion

It has been recognized for almost 15 years that two-point nucleotide correlations within a single genome can exhibit power-law behavior (13–15). The original studies revealed a tendency for correlations in protein-coding exons to exhibit exponential decay, whereas “noncoding” sequence, for example from selected introns, showed power-law decay. These early observations from the physical sciences community were reported when the prevailing opinion among biologists was that with the exception of classical protein-coding exons and some nearby regulatory elements, the bulk of the genome was composed mainly of nonfunctional “junk.” The power-law correlations were rationalized at the time as a consequence of the repetitive structure that is often a feature of (generally assumed to be nonfunctional) sequence in noncoding regions (16), and it remains an open question whether the intra-genomic power-law correlations can, by themselves, distinguish functional from nonfunctional noncoding sequence (for a review, see ref. 17).

The 2002 comparison (7) of the newly completed human and mouse genomes altered the perspective of many biologists when it was found that (i) there was not enough conserved protein-coding sequence to account for the complexity of higher eukaryotes, and (ii) whereas strong conservation of 2% of the sequence between these genomes could be accounted for by protein-coding sequence, an additional 4% could not. Although there had been previous indications that much of the sequence of these genomes had nonclassical functions, perhaps representing undiscovered regulatory elements or genes for so-called “noncoding” RNAs, recent years have seen a vast expansion of the quantity, variety, and scope of functional sequence that does not code for proteins. In particular, the RIKEN FANTOM3 consortium demonstrated recently (18) that on the order of half of each strand of the mouse genome is transcribed—although within these transcripts, roughly half of previously discovered noncoding RNAs remain undetected.

One obstacle to recognizing the significance of the early power-law data is that sequence correlations, some exceptions such as those arising from the classical triplet codon aside, have generally admitted no natural biological interpretation. For example, a functional role for intragenomic fluctuations of GC content, which certainly display nontrivial scaling properties (10), remains speculative. The current paradigm of molecular biology is largely based on “motifs” and other local structures such as genes. The observations described here fit this paradigm: We identify by general considerations a class of sequence, relatively short on the genomic scale, that we expect to fulfill novel and important biological roles.

On the other hand, the location of functional elements within a genome is known to be closely coordinated with their expression. The relative location of HOX genes within a HOX cluster influences the order of their spatial and temporal expression. Micro-RNA expression has been shown to be correlated with the expression of nearby genes (19). Observations of scaling over more than two orders of magnitude in length have recently been reported for organization of genes within microbial chromosomes (20), and a scaling regime of 10–200 bases in eukaryotes has been reported that may be related to positioning of nucleosomes (21). Both of these latter phenomena are intragenomic and more limited in dynamic range.

The characterization and modeling of power-law correlations within genomes has undergone steady refinement since 1992, when Li (22) proposed that they could be accounted for by a simple model of neutral evolution, the “expansion-modification” model. Most recently, the scaling of correlations in the expansion-substitution model and some natural generalizations have been derived analytically and the decay of correlations directly related to λ, the ratio of the rate of expansion to the rate of substitution (23). Substitution, possibly together with insertion and deletion at fixed total length but without expansion, yields exponentially decaying base–base correlations; turning on expansion in the form of single-base duplication is then sufficient to yield the power law. Most interestingly, although there is no phase transition in the two-point correlations as a function of λ, there is a critical value of λ above which base probabilities retain a memory of initial sequence composition. This observation underscores the importance of distinguishing correlations in and conservation between genomes that are consequences of selection rather than of the “memory.”

Other Organisms.

As illustrated in Fig. 2 (curves b and c), whole-genome alignment can reveal algebraic distributions in regimes where intersection (curve d) is dominated by coincidences. For example, fly/bee whole-genome alignment reveals a power law from 10 to 30 bases that is entirely obscured in intersection of those genomes. Where alignments are readily available, algebraic distributions of perfectly conserved sequence appear to be general phenomena, provided the genomes are not too closely related. The latter restriction is not entirely unexpected, because eventually a crossover to distributions characteristic of whole-genome self-alignment is inevitable. Intersections and alignments among Drosophila subspecies and between human and chimp exhibit this more complex behavior (illustrated for Drosophila in Fig. 8, which is published as supporting information on the PNAS web site).

For sufficiently distantly related species, whole-genome alignment exhibits power-law regimes not only in metazoans, but in plants, yeast, and bacteria as well. Remarkably, these powers tend to fall within a fairly narrow range, suggestive of universal limits as genomes diverge (J.M., unpublished data).

Perfectly Conserved Sequence.

The strong enrichment for known functional elements in sequences perfectly conserved among multiple vertebrates has been demonstrated in other contexts (1) (T. Tran, P.H., and J.M., unpublished data). For 26 ≤ L ≤ 50, they are particularly enriched for mature micro-RNAs, other noncoding RNAs, micro-RNA targets, and transcription factor binding sites, often by factors of 1,000 or more over whole genome. This observation alone indicates that perfectly conserved sequences are subject to strong negative selective pressure. Protein motifs such as homeodomains are also represented, specifically as coding sequences that, subject to codon bias, can sustain little if any variation without altering the amino acids they encode; however, their enrichment is lower by orders of magnitude. As stressed in ref. 24, a distinctive property of these functional elements is that they are subject to multiple nonlocal constraints. A highly conserved micro-RNA, for example, may regulate tens or hundreds of distinct targets. For a mutation in the mature micro-RNA sequence to be sustained, independent compensatory mutations in each of these targets would be required, an extremely unlikely set of events under neutral drift. Enhancers are comprised of multiple and overlapping transcription-factor-binding sites. A mutation in the enhancer would require compensatory changes within the transcription factors whose binding sites overlap the mutation.

These observations suggest that perfectly conserved sequences arise from their combinatorial interaction with multiple and remotely located parts of a genome—either directly, in the case of the complementary base pair mediated interactions of micro-RNAs and other small RNAs, or indirectly, in the case of protein–DNA binding (25). Thus, the “digital” (in contrast to “analog”) encoding mechanism postulated by Mattick may be a consequence of the sequence constraints entailed by overlapping combinatorial sequence interactions, e.g., a single micro-RNA regulating multiple distinct targets, and a single target being regulated by multiple distinct micro-RNAs.

Mattick (26) has conjectured the role of a “hidden layer” of regulatory RNA in multicellular organisms as a network of regulatory elements whose number scales as the square of the number of proteins that they regulate; these regulatory elements, and not the number of protein-coding genes, are what he argues distinguish mammals from worms. The strong enrichment for noncoding RNA among perfectly conserved sequences suggests to us that this network may be comprised in part by sequences strongly constrained by overlapping combinatorial interaction, and that the scaling of perfectly conserved sequence lengths may reflect this network of regulatory elements.

Finally, as illustrated in Fig. 2 (curve j) and Fig. 5, for highly conserved sequence in the CFTR locus, the phenomena described here extend well beyond perfect conservation.

Information.

Our definition of maximal L-mer is reminiscent of the (symmetric) “match-length,” defined for the purpose of computing intragenomic entropy (27, 28) as the length of the shortest sequence starting at position i that is not contained elsewhere in the genome (or equivalently of the longest sequence starting at position i that is contained elsewhere in the genome). It seems plausible to us that the mutual information between two genomes may be related via match-length to maximal L-mers and their length distribution.

Conclusions.

Our principal observation is that the lengths of sequences perfectly conserved between mouse and human genomes are distributed algebraically (Figs. 1 and 2). This scale-invariance manifests itself in the algebraic distribution of spatially local objects (inter-genomic highly conserved sequence) rather than merely in nonlocal constructs such as intra-genomic two-point correlations. It is not obvious that the power-law distribution of lengths is entailed by long-range correlations alone; although we expect that a model of neutral drift that yields this power-law distribution can be conceived, the vast enrichment for functionality among these sequences suggests to us an essential role for selection. The spatial correlations and clustering of perfectly conserved sequences within the mouse genome (Figs. 3 and 4) indicate self-similarity at much greater scales as well. Conservation can be closely associated with functionality, so that our observations highlight the urgency of addressing the biology that drives scale-invariant organization of genomic sequence.

Methods

Identifying Mouse/Human Maximal L-mers.

The repeat-masked mouse genome [Mus musculus NCBI Build 34 (mm6)] and the repeat-masked human genome [Homo sapiens NCBI Build 35 (hg17)] were obtained from the UCSC genome browser (29). Sequence perfectly conserved between these two genomes was computed in several different ways: (i) as described in ref. 4 by L-mer intersection, a process that neglects sequence location; (ii) based on whole-genome alignments obtained from UCSC, again as described in ref. 4; and (iii) in such a way as to retain location (for details, see Supporting Methods, which is published as supporting information on the PNAS web site). We have applied the same procedures to multiple versions of the mouse and human genome sequences (hg16, hg18, mm5, mm6, mm8) and observed no differences in the outcome of the computations reported here.

Highly Conserved Sequence from Alignments of CFTR Loci.

In ref. 11, ≈1.9 megabases of genomic sequence encompassing the CFTR locus from 29 mammals were aligned, gapped positions were discarded, and expected rates of substitution for each position were determined based on phylogeny via maximum likelihood. At each position, the ratio of the observed to the expected substitution rate was computed. The difference between observed and expected rates was summed over runs of positions with sufficiently low ratio to yield the rejected substitutions, or RS. If the RS was below a specified threshold, the run was classified as a “highly conserved” sequence. To serve as a standard, a null model was derived by randomly permuting the substitution rates in space and once again extracting runs of sequence as described above.

To produce the figures shown here, files containing the expected and observed rates of substitution at each position of the alignment were downloaded as http://mendel.stanford.edu/supplementarydata/cooper_GERP_2005/CooperEtAl_RawData.zip.