Influence of spatial heterogeneity on an emerging infectious disease: the case of dengue epidemics

Abstract

The importance of spatial heterogeneity and spatial scales (at a village or neighbourhood scale) has been explored with individual-based models. Our reasoning is based on the Chilean Easter Island (EI) case, where a first dengue epidemic occurred in 2002 among the relatively small population localized in one village. Even in this simple situation, the real epidemic is not consistent with homogeneous models. Conversely, including contact heterogeneity on different scales (intra-households, inter-house, inter-areas) allows the recovery of not only the EI epidemiological curve but also the qualitative patterns of Brazilian urban dengue epidemic in more complex situations.

1. Introduction

Over the past few decades, the world has experienced the emergence, or the re-emergence, of several infectious diseases in connection with fast-changing environment, population growth, human migration and international travel (Cohen 2000). An example of these emerging diseases is the resurgence of dengue (Gubler 2002a). Dengue is a human arboviral disease, which is mainly transmitted by the domestic mosquito Aedes aegypti—even though other Aedes (e.g. A. albopictus and A. polynesiensis) can also act as vectors. The dengue virus belongs to the Flaviviridae family and has four distinct serotypes DEN-1, -2, -3 and -4 (see Rigau-Pérez et al. 1998 for a detailed description).

Dengue has been known since the late eighteenth century as a benign flu-like syndrome appearing sporadically, with intervals of 10–40 years. Over the past few decades, the expansion of this disease in Southeast Asia and South America and the increase of benign and lethal forms (Gubler 2002b; Guzmàn & Kouri 2002) have been observed. The different forms of dengue—dengue fever (DF), dengue haemorrhagic fever (DHF) and dengue shock syndrome (DSS)—constitute one of the most important re-emerging tropical diseases at the beginning of the twenty-first century. It has been estimated that 50–100 million people suffer from dengue each year, and that half of the human population lives in areas at risk (Gibbons & Vaughn 2002).

The resurgence of epidemic DF and the emergence of DHF/DSS have been connected to societal changes such as population growth, urbanization (Guzmàn & Kouri 2002) and the transport of infected hosts and vectors (Gubler 2002a). Furthermore, rising temperatures and global climate change may be leading to the expansion of the range of A. aegypti in both time and space, thereby exposing host populations to a longer transmission season and immunologically naive populations to the newly introduced virus (Epstein et al. 1998; Patz & Reisen 2001; Hales et al. 2002). Finally, the increase of the severity of dengue, even in primary infections, suggests an evolution of the virulence of dengue strains (Holmes & Burch 2000). In the end, although the factors at the origin of this emergence are qualitatively known, the way they interplay is not clearly understood (Schrag & Wiener 1995; Gubler 2002a). The development of models to describe the interactions of these different factors and their effects on the transmission of the dengue virus are of fundamental importance for understanding and predicting the patterns of dengue epidemics. Modelling dengue dynamics can help us to understand, locally, the influence of the different parameters and, on a larger scale, the mechanisms of emergence.

In dengue epidemics, the hosts (i.e. humans) lie at the centre of the epidemic process. Contrary to other arboviral diseases that primarily affect animals (e.g. cattle for the Rift Valley fever, birds for West Nile fever), transmission from human to human via the mosquito is the only way dengue can spread. As with other diseases (Grenfell & Bolker 1998), the spatial dynamics of dengue are potentially influenced by human behaviour; in other words, by the spatial and social structure of the human population (geographical separation of neighbourhoods or villages, separations along lines of social interaction or social segregation). On a local scale (a neighbourhood or a village), can the contacts between hosts and vectors be assumed homogeneous? If not, how does the population structure influence the epidemic dynamic?

Although recent epidemiological models of certain diseases include the role of spatial and social networks for the spread of epidemics, dengue models do not incorporate the spatial structure (e.g. Newton & Reiter 1992; Esteva & Vargas 1998). We have based our study on the Easter Island (EI) epidemic, where a relatively small, initially immunologically naive population is concentrated in a single village on an island. We show that, even in the most simple case, contact heterogeneity must be considered to reproduce the epidemiological curve. We then compare the qualitative pattern of the modelled epidemics with other urban epidemics in Brazil with different initial conditions and in open environments.

2. Models

To determine the influence of local heterogeneity in the epidemic, the data are confronted with two models. The null model assumes homogeneous mixing between host and vector population, while heterogeneity of contacts is considered in the second model. Parameters definitions and values are summarized in table 1.

Table 1.

Summary of the parameters of the model with their notations, the range of values in literature (from Luz et al. 2003), the range of values used to test the homogeneous model and the values for the EI case. EI, Easter Island; EIP, extrinsic incubation period; IIP, intrinsic incubation period.(* in the 5% infested households, no vector at all elsewhere, which correspond to 1.5 vectors per host in the whole population.)

actor	parameter	notation	range in theliterature	range for simulations	value for EI
vector	total number per host	k	0.3–3	1–10	30*
	duration of the EIP	tEIP	7–12	4–12	6
	daily mortality	m	0.1–0.3	0.1–0.9	0.2
	contact rate with viraemic hosts	ch→v	0.4–0.9	0.1–0.9	0.9
host	daily probability to leave the intrinsic incubation period	pIIP	IIP of some days	0.1–0.6	0.22
	daily probability to leave the viraemic period	pr	viraemia of 3–5 days	0.1–0.6	0.2
	contact rate with infective vectors	cv→h	0.4–0.9	0.1–0.9	0.8

(a) Null homogeneous model

The homogenous model is based on the classical hypothesis that each vector can bite any host with equal probability. The populations are divided into classes in relation to the disease: susceptible (S), incubating or exposed (E), infective (I) and immunized or removed (R).

The vectors are represented by a discrete-time aggregated SEI model, slightly modified from Anderson & May (1991). We set V_s, V_i, V_v to be the populations of susceptible, incubating and infective vectors, respectively, and ΔV(t) to be the variation of the population between day t and day t+1. The model is represented as follows:

$$\begin{array}{l}\mathrm{\Delta }{V}_{\text{s}}\left(t\right)=-m\cdot V_{\text{s}}(t)+r[V_{\text{s}}(t)+V_{\text{i}}(t)+V_{\text{v}}(t)]\times \left(1-\left(1-\frac{m}{r}\right)\frac{V(t)}{k\cdot H(t)}\right)-c_{\text{h}\to \text{v}}\frac{H_{\text{v}}(t)}{H(t)}{V}_{\text{s}}(t)\hfill \\ \mathrm{\Delta }{V}_{\text{i}}\left(t\right)=-m\cdot V_{\text{i}}(t)+c_{\text{h}\to \text{v}}\frac{H_{\text{v}}(t)}{H(t)}{V}_{\text{s}}(t)-{(1-m)}^{t_{\text{EIP}}}\times c_{\text{h}\to \text{v}}\frac{H_{\text{v}}(t-t_{\text{EIP}})}{H(t-t_{\text{EIP}})}{V}_{\text{s}}(t-t_{\text{EIP}})\hfill \\ \mathrm{\Delta }{V}_{\text{v}}\left(t\right)=-m\cdot V_{\text{v}}(t)+{(1-m)}^{t_{\text{EIP}}}\times c_{\text{h}\to \text{v}}\frac{H_{\text{v}}(t-t_{\text{EIP}})}{H(t-t_{\text{EIP}})}{V}_{\text{s}}(t-t_{\text{EIP}}),\hfill \end{array}$$

Death and birth are described in classical logistic terms, where the number of deaths is proportional to the number of vectors (m is the daily vector mortality), and the birth term contains a competition term that ensures the convergence to a total amount of kH mosquitoes (r is the basic recruitment rate, H is the number of hosts—each of which can sustain a population of k mosquitoes—and k is directly dependent on the number of bites per day that an individual host can experience, and which can evolve in accordance with climatic variations or vector control measures). Each day, each mosquito bites, on average, a times (a can be less than 1). The number of bites by susceptible mosquitoes is aV_s. Assuming that mosquitoes bite any host with equal probability, then the proportion of bites of susceptible mosquitoes biting viraemic hosts is equal to the proportion of viraemic hosts in the population (H_v/H, where H_v is the number of viraemic hosts). Of these bites, only a fraction b will eventually lead to the infection of the vector. The product ab is the effective contact rate between viraemic hosts and susceptible mosquitoes and is denoted by c_h→v (host to vector). Assuming that the extrinsic incubation period (EIP: the time necessary for the virus to follow the cycle that brings it from the mosquito's stomach to its salivary gland) is a constant (t_EIP), then the mosquitoes changing status from incubating to infective are those that were infected t_EIP days before and that outlived this period: their proportion is ${(1-m)}^{t_{\text{EIP}}}.$

The host population is represented by an individual-based SEIR model: here, the fate of each host is described (DeAngelis & Gross 1992). The transitions between the S, E, I and R states are stochastically modelled. As c_h→v, we define c_v→h to be the effective contact rate between infective vectors and the susceptible hosts, it is the product of the number of bites per day by an infective vector and the proportion of infective bites that eventually lead to host infection. The mean number of infective bites per day is c_v→hV_v and the probability that a susceptible host is bitten (assuming that this probability is homogeneously distributed among hosts) is c_v→h(V_v/H). If a susceptible host is bitten by an infective vector, then it becomes infected unless it has already encountered the same virus and is immune. Once infected, the host will enter the viraemic phase with a probability p_IIP per day. Subsequently, the host has a probability p_r per day of recovering and becoming immune to the current strain (so far, co-circulating viruses are not considered).

(b) Heterogeneous model

In the heterogeneous model, we assume that the heterogeneity of contacts emerges from the structure of the populations of vectors and hosts in households. The homogeneous mixing hypothesis is still supposed to hold in each household. In addition, the contacts between households are ensured by hosts' movements, as the vectors are tied to the household.

This kind of heterogeneity can be characterized by a single parameter π, which is the daily probability for each host to visit the host population of another house, randomly chosen—and thus to participate in its algorithm—then return to his home. The population of a house can thus become infected in two ways: (i) by the visit of a viraemic host, or (ii) through the infection of a susceptible host while staying in another house (already infected).

3. Data

Three sources of data are compared with the model outputs: the EI epidemic in 2002, the epidemics in Belém, Para in 1997 (Mondet et al. 1997) and Brasília, Federal District (Brazil) in 2002. These epidemics differ in nature and in the information which can be extracted from them.

The epidemiological curve in EI is taken from Aguilera et al. (2002). There, the whole population (approximately 3600 people) is concentrated in one village and was previously unaffected by dengue. The DEN-1 virus involved in the epidemic (Perret et al. 2003) was imported from French Polynesia (FP), where it created an epidemic at the end of 2001 (Hubert 2001). Some information is lacking; notably, the proportion of people infected was not reported (some of them may not have been registered with the medical staff or they may have had an asymptomatic form of the disease). However, limits as to the proportion of asymptomatic people can be estimated by considering that the proportion of asymptomatic forms caused by this virus cross-secondary infection (with a different serotype) was lower than those in primary infections. The lower limit is obtained by assuming that the proportion of asymptomatic secondary form was equal to that of primary forms, while the upper limit is obtained by assuming that there was no asymptomatic form in cross-secondary infections. Calculations from the figures of Hubert (2001) yield a proportion of asymptomatic forms between 30% and 74%. The characteristics of the EI epidemic thus inferred are summarized in table 2.

Table 2.

Characteristics of Easter Island dengue epidemic in 2002 (from Aguilera et al. 2002).

prevalence (% population)	peak height (% population)	epidemic duration (days)	peak day (from the epidemic beginning)
22–58	0.7–2.7	76	21

The epidemiological data of the Brasília and Belém epidemics were reported by the Brazilian Health Ministry. In Brazil, successive dengue epidemics have occurred since 1982 (Degallier et al. 1996), and the proportion of the susceptible population before these epidemics is not known. Therefore, the study is limited to the qualitative pattern of the epidemic dynamic in these cases (in particular, the final prevalence cannot be computed).

4. Methods

We first explored the model behaviour, assuming a homogeneous host population. The number of hosts was fixed to a large arbitrary number (1000) in order to limit noise. We randomly varied the parameters in the range indicated in table 1 corresponding to realistic values. We simulated 3000 random sets of parameters, with two infectious hosts and a totally uninfected vector population as initial conditions. Four variables are used to characterize the epidemic peak: two time characteristics (duration of the epidemic and peak day from the beginning of the epidemic) and two population characteristics (final prevalence and peak height (the maximum number of people per day declaring dengue)).

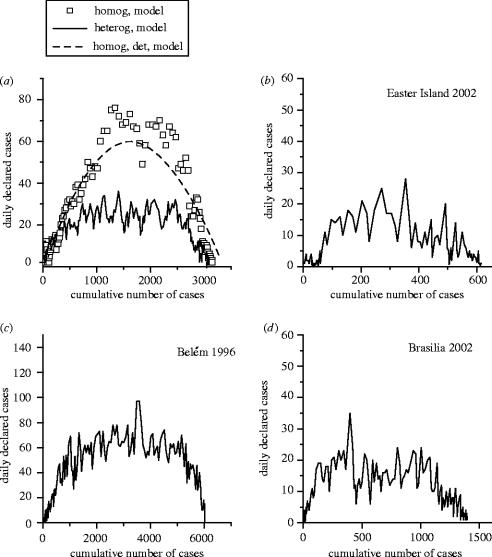
In the second step, we explored the influence of household heterogeneity on these characteristics and on the epidemic development. We define N(t) as the cumulative number of dengue declarations at time t (as the sum of the number of infective and removed hosts at time t) and ΔN(t)=N(t)−N(t−1) as the daily number of declarations. Traditionally, epidemiological curves represent the time evolution of N(t). Instead, we characterize the epidemic development by a plot of ΔN(t) against N(t) (the phase space of the variable N). As shown in figure 3d, this approach more effectively determines the beginning of an epidemic after a phase of low level circulation. We determine how the phase space N is changed by the introduction of contact heterogeneity and compare it with the phase space of real epidemics.

Figure 3.

Epidemiological curves: new cases declared daily versus cumulative number of cases. (a) Individual-based modelled epidemics, with and without household heterogeneity. The dashed line represents the pattern of the homogeneous model written in differential equations. (b–d) Real epidemics in the Easter Island, in Belém and in Brasília. As in the heterogeneous model, a plateau follows an initial linear growth before extinction.

5. Results

(a) Epidemics in a homogeneous population

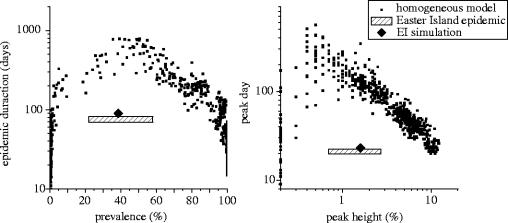
In a large homogeneous population, the outcome of our individual-based model without heterogeneity is similar to that of a classical difference equation model, like that used in Anderson & May (1991) and Newton & Reiter (1992), with a peak in the number of daily new viraemic hosts and a delayed peaks for the infective vectors (figure 1). Figure 2 presents the relationship between time characteristics of the epidemics. Results show a strong nonlinear association between time and population characteristics (figure 2). These epidemiological features evaluated for the EI epidemic (table 2) are clearly outside the cloud of points computed with the homogeneous model.

Figure 1.

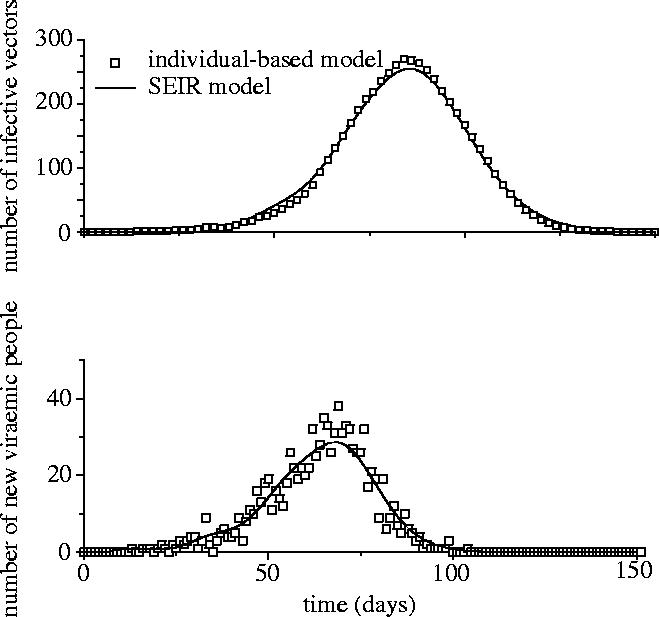
Evolution of the number of infective vectors (top) and the number of new viraemic hosts per day (bottom) using the individual-based model (open squares) without spatial parameters and the discrete-time version of the classical differential equation model (the daily number of new viraemic hosts being $c_{\text{h}\to \text{v}}{V}_{\text{i}}(t-t_{\text{IIP}})H_{\text{s}}(t-t_{\text{IIP}})/H$, where H_s is the number of susceptible hosts and t_IIP the intrinsic incubation period).

Figure 2.

Link between time and populations characteristics for epidemics simulated by the homogeneous model. Each black square represents the output of the model run with 1 of 3000 random parameter sets. The range of possible values for the same characteristics in the Easter Island case (from table 2) is displayed in the same graphs.

(b) Influence of contact heterogeneity

The heterogeneity of contacts induces changes in the epidemic pattern, which are particularly perceptible in the phase space of the cumulative number N of dengue cases. With homogeneous contacts (figure 3a), the line initially progresses in a straight direction (which tallies with the initial exponential phase of the epidemic growth), progressively curves and finally decreases. The structure of the population in households results in a similar beginning but in a saturation to a nearly constant value in the middle of the curve, which corresponds to a linear increase in the cumulative number of cases. A similar pattern is found in the plots of real epidemics, as shown in figure 3.

(c) Dengue in Easter Island

Aguilera et al. (2002) showed discrepancies in vector infestation rate between areas in EI. In the absence of detailed data, we chose a realistic representation of this situation. It appears possible to simulate an epidemiological curve similar to the real one in considering a two-level household-based heterogeneity with the parameters summarized in the last column of table 1 (figure 4). On the first level, 3600 people are grouped into 10-people households. On the second level, households are grouped into areas of 60, with the probability of contacts between households in the same area (p=0.5) being greater than the probability of contacts between households of different areas (p=0.05). Only 5% of the households are infested (Aguilera et al. 2002), with all households concentrated in the same area. The other parameters were chosen within the possible range to ensure that the real and the simulated curves were as close as possible (figure 4). The static characteristics of this simulated epidemics are displayed in figure 2 and match the range estimated for the real epidemic.

Figure 4.

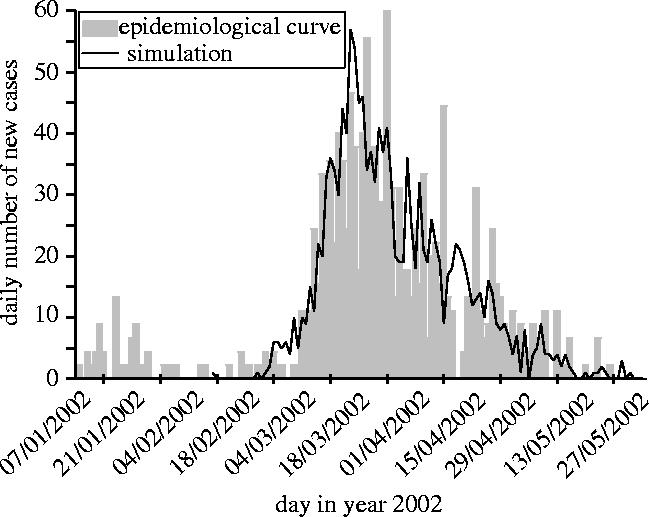
Comparison between the time evolution of number of reported cases in the real Easter Island epidemic (Aguilera et al. 2002) and the model output with a two-level spatial structure.

6. Discussion

To date, models of the dynamics of dengue epidemics have assumed homogeneous mixing of the human and mosquito populations. This was justified by the purposes of the studies as qualitative evaluations of the effect of different types of vector control (Newton & Reiter 1992; Miorelli & Adami 1999) or as computations of the possible evolution of seroprevalence over time (Focks et al. 1995).

However, these simple models are unable to describe epidemics on a local scale. The comparison with the 2002 epidemic in EI is particularly interesting for two reasons. First, the whole population can be assumed susceptible before the epidemic and, second, the population is strongly localized. Even in this simple scheme, the homogeneous model is unable to reproduce the static characteristics of the EI epidemic. Indeed, the static properties of homogeneous mixing-based models are constrained and not compatible with the same characteristics evaluated for the EI epidemic.

Some heterogeneity must therefore be considered even on a local scale. Including two-level heterogeneity allows the researcher to recover an epidemiological curve similar to the observed one in the EI. Of course, other factors may intervene and were not considered, especially the under-reporting of causes, vector control efforts during epidemics and seasonal variation of climatic conditions influencing the vector population. For example, the pre-epidemic period may be explained by a lower level of mosquito density or by the circulation of the virus in areas where mosquitoes were rare before the virus reached the most infested area. For these reasons, we do not claim that our simulation is anything more than an illustration of the necessity of including heterogeneity to represent the development of an epidemic, even on a local scale.

However, our study provides further indications that it is necessary to consider the natural structure of the population, partitioned by households. Indeed, this allows the recovery of the qualitative patterns of real epidemics in more complex situations than in the EI, Brasília or Belém, where the initial exponential growth of the epidemic is followed by a period when the cumulative number of cases grows linearly before the saturation. Quantitative simulations in these cases are hindered by a lack of information about the initial immunological status of the population (for Brasília), the proportion of infested houses in the different districts, and so on. From a qualitative point of view, the proportion of infested houses and the population density (in the districts where epidemics took place) were certainly greater in Belém than in Brasília, which means that the degree of heterogeneity was less. This can explain why the Belém epidemic pattern was closer than the Brasília epidemic to the homogeneous model.

To conclude, this paper underlines the critical influence of the spatial structure of population, even on a local scale. On a local scale, the influence of the contact network on the spread of diseases has been studied for sexually transmitted diseases (Anderson et al. 1990; Friedman & Aral 2001; Klovdahl 2001; Eames & Keeling 2002). Recent studies in theoretical epidemic modelling have focused on the influence of two scales of contact, local and global, in ‘small world’ models (Moore & Newman 2000; Kuperman & Abramson 2001), cellular automata (Turner et al. 2003) or the households model (Ball & Neal 2002). In the latter model, as in our simulations, the contact between people happens on two levels: (i) a local level (contacts within a household), and (ii) a global level (possibility of contacts between people belonging to different households). In the case of dengue, this study suggests that the structure of the human population and of the contacts between humans and mosquitoes are important determinants for the evolution of an epidemic. These theoretical considerations are confirmed by recent field studies that also reported heterogeneity in incidence of dengue on a town scale (Bohra & Adrianasolo 2001; Aguilera et al. 2002), which was correlated with the hygiene conditions and consequent mosquito density (Bohra & Adrianasolo 2001). It appears that the number of contacts between host and vector is highly dependent on socio-economic and cultural factors, such as hygiene and vector control.

In the future, the degree of heterogeneity in real situations and its effect on epidemic development will have to be quantified through theoretical research and field studies. Furthermore, this model can be extended further to a hierarchical model that is able to describe an epidemic at a larger geographical scale. The use of Geographic Information Systems technology could allow the development of a model that could describe the epidemic dynamics on regional or national scales. Additional parameters such as virulence of the virus and host genetic predisposition may also play a role and need to be assessed in a more realistic model as well as in field studies.