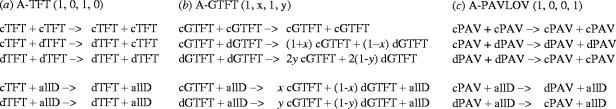Evolution of cooperation by generalized reciprocity

Abstract

The evolution of cooperation by direct reciprocity requires that individuals recognize their present partner and remember the outcome of their last encounter with that specific partner. Direct reciprocity thus requires advanced cognitive abilities. Here, we demonstrate that if individuals repeatedly interact within small groups with different partners in a two person Prisoner's Dilemma, cooperation can emerge and also be maintained in the absence of such cognitive capabilities. It is sufficient for an individual to base their decision of whether or not to cooperate on the outcome of their last encounter—even if it was with a different partner.

1. Introduction

Studies on the evolution of altruistic behaviour among organisms that are selected for their individual fitness are often based on the Prisoner's Dilemma (PD) (Axelrod & Hamilton 1981; Axelrod 1984; Boyd & Richerson 1988; Nowak & Sigmund 1992, 1993; Dugatkin 1997). Two individuals that interact in a PD, simultaneously have the choice between cooperation (C) and defection (D). If both individuals cooperate, they gain a ‘reward’ (R), whereas if both individuals defect they only receive a ‘penalty’ (P). If, however, one individual cooperates and the other defects, the defector is rewarded by the highest payoff, ‘temptation’ (T), whereas the cooperator receives the lowest payoff, ‘sucker's payoff’ (S). Given the payoff structure of the PD T >R >P >S and 2R>T+S, it always pays to defect, irrespective of the partner's choice. Thus cooperation cannot evolve if individuals interact only once in a ‘one-shot’ PD. Cooperation, however, can evolve if individuals interact repeatedly, as in the iterated Prisoner's Dilemma (iPD). In the iPD, strategies that allow individuals to base their behaviour on the outcome of previous interactions with the present partner, such as tit-for-tat (TFT), may establish cooperation in a population of selfish individuals (Axelrod & Hamilton 1981; Axelrod 1984; Nowak & Sigmund 1992, 1993). This mechanism for the evolution of cooperation is often referred to as ‘direct reciprocity’ because individuals can reciprocate previous cooperative behaviour of their partners (Trivers 1971). Direct reciprocity, however, can only be successful if individuals recognize their partner and remember the outcome of their previous encounter, or if individuals interact with only one partner for a long time (Dugatkin 2002). Thus, direct reciprocity either requires specific cognitive capabilities of the interacting individuals (Milinski & Wedekind 1998) or requires a very specific population structure such that the latter mechanism can take effect.

Behavioural studies on humans (Berkowitz & Daniels 1964) and a novel behavioural study on rats (Rutte & Taborsky submitted), however, indicate that individuals may base cooperative behaviour on prior experiences—irrespective of the identity of their partners. Such behaviour is referred to as generalized reciprocity (Rutte & Taborsky submitted). In contrast to direct reciprocity, generalized reciprocity does not require such advanced cognitive skills as partner recognition and memory of previous encounters, but relies only on the ability of an individual to judge the outcome of its most recent interaction. Although mechanisms similar to generalized reciprocity have been studied in the field of economics (Kandori 1992), there are so far, to our knowledge, no theoretical studies analysing whether generalized reciprocity can evolve from a non-cooperative population, and can maintain cooperation in a population. Here, we show that if individuals interact repeatedly in small groups, then it is sufficient for the evolution and maintenance of cooperation that individuals base their behaviour towards the present partner on the outcome of the last encounter they had, irrespective of the identity of the partner.

2. Simulations for the evolution of generalized reciprocity

To study whether cooperation can evolve and be maintained in a population by generalized reciprocity, we use population dynamical simulations, analogous to those used for studying direct reciprocity (Nowak & Sigmund 1993, 1994). We assume that the population consists of groups of n individuals. Here, we first describe simulations for groups of three individuals and then discuss generalized reciprocity in larger groups. We assume that individuals interact repeatedly within their group. In each round, two individuals of a group are chosen randomly to interact in a ‘one-shot’ PD. After a sufficiently large number of interactions such that the average payoffs can be approximated by the payoffs for an infinite number of interactions (Nowak & Sigmund 1993, 1994), the groups are dissolved and new groups are formed randomly from the population. Furthermore, we assume that individuals do not recognize their partners and base their decision solely on the outcome of their last encounter within the group. Thus, individuals use ‘memory one’ strategies that are described by four probabilities (p₁, p₂, p₃, p₄), namely the probabilities of cooperating after the payoff of the last encounter was R, S, T or P, respectively. Note that in contrast to direct reciprocity, where these probabilities describe the response of an individual to the previous encounter with the present partner, here these probabilities describe the response of an individual to its last interaction within the group. To emphasize this essential difference between strategies of direct and of generalized reciprocity, we refer to the latter as anonymous (A–) strategies. A detailed description of the simulations is given in Appendix A. A typical simulation is shown in figure 1.

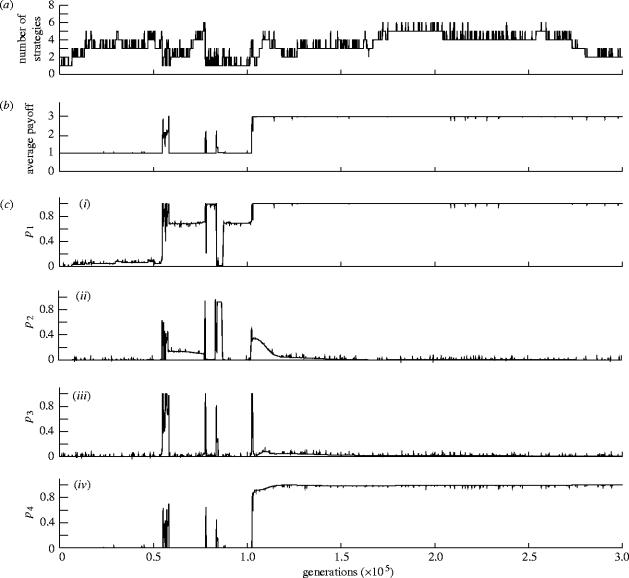
Figure 1.

Simulation of the evolution of strategies for generalized reciprocity for group size three. The figure shows (a) the number of strategies present in the population, (b) the average payoff per individual per encounter, and (c) the average probabilities ((i) p₁, (ii) p₂, (iii) p₃, (iv) p₄) that characterize the strategies in the population. We start with a population of unconditional defectors. New strategies are inserted on average once per 100 generations. In the simulation, A-TFT emerges after about 55 000 generations and establishes cooperation. Then, more generous strategies evolve and eventually allow defecting strategies to invade. Here, a retaliator-like strategy close to (0.68, 0.14, 0.001, 0.001) wins and dominates the population until about generation 80 000. Subsequently, cooperation is re-established twice for very short periods, until A-TFT again establishes cooperation shortly after generation 100 000. Again, more generous strategies invade, but this time, A-PAVLOV-like strategies with values close to (0.999, 0.001, 0.001, 0.999) take over and eventually outcompete A-GTFT. A-PAVLOV dominates the population for the remaining time of the run.

3. Results

In all of the simulations, cooperation evolves and is stably maintained in the population by anonymous strategies. The emerging strategies are analogous to those emerging in simulations of direct reciprocity, namely to PAVLOV (sometimes referred to as ‘win–stay, lose–shift’; Nowak & Sigmund 1993), and to generous tit-for-tat (GTFT; Nowak & Sigmund 1992): we observe A-PAVLOV described by probabilities close to (1, 0, 0, 1) dominating 62% of the runs with average frequencies of more than 90% over the complete length of a simulation, and A-GTFT-like strategies with probabilities of around (1, 0.5, 1, 0.2) dominating 38% of the runs. Populations are usually homogeneous once A-PAVLOV dominates, but are heterogeneous, often with more than 10 coexisting strategies, when A-GTFT-like strategies dominate. Similar to TFT in studies on direct reciprocity, A-TFT, characterized by probabilities close to (1, 0, 1, 0), never dominates a run for long periods, but plays an important transient role for establishing cooperation in a non-cooperative population. Generally, our findings are remarkably similar to the results of the studies on direct reciprocity (Nowak & Sigmund 1993), given that in contrast to direct reciprocity, in our model individuals do not know whom they are interacting with. (For comparison, a simulation for the evolution of direct reciprocity is shown in figure 1 of the Electronic Appendix.) Starting from a non-cooperative population, A-TFT establishes cooperation in a similar way as does TFT in direct reciprocity: in groups that consist exclusively of A-TFT players, individuals cooperate at a frequency of 0.5 (owing to the effect of occasional mistakes), as a pair of TFT players does in direct reciprocity (Nowak & Sigmund 1992, 1993). If, however, there are non-cooperative individuals in the group, A-TFT players refrain from their high level of cooperation and cooperate only slightly more frequently than non-cooperative individuals. Thus, if present at a sufficient initial frequency, the high individual payoff in groups that consist exclusively of A-TFT players compensates for the slight disadvantage of A-TFT in the presence of defectors. This frequency is higher for groups of three individuals using A-strategies compared with two individuals using direct reciprocity. Thus we choose a comparatively high initial frequency of new strategies in our simulations (see Appendix A).

An intuition for the successful behaviour of A-TFT is that in contrast to TFT, where defection is reciprocated directly, A-TFT indirectly reciprocates non-cooperative behaviour of an individual by defecting towards another individual in the group, which at a later interaction may defect towards the non-cooperative individual.

Once A-TFT has established cooperation at a frequency of 0.5, more generous strategies that cooperate at a certain probability even after the last partner defected, such as A-GTFT, can spread and increase the frequency of cooperation to levels close to 1.0. Too much generosity, however, invites defecting strategies—and A-PAVLOV, a cooperative strategy that can exploit unconditional cooperators. In summary, our simulations show that if individuals interact in groups of three, cooperation can be established by generalized reciprocity. Thus, it is not necessary for the evolution and maintenance of cooperation to distinguish between the two other partners in a group. Note that although the population is structured in groups, in our model, cooperation is not facilitated by spatial clustering of unconditional cooperators (Nowak et al. 1994) or group selection (Wilson 1975), as it is in many other studies on the evolution of cooperation (van Baalen & Rand 1998; Hauert 2001). In our model, groups are formed randomly, there is no selection between groups, and strategies interact with all other strategies in all possible combinations.

4. Generalized reciprocity in larger groups

Generalized reciprocity may also be a mechanism for the evolution of cooperation if individuals interact in groups with more than three individuals. Since cooperation can at least temporarily emerge by generalized reciprocity if A-TFT is capable of invading a non-cooperative population, conditions for the evolution of generalized reciprocity can be approximated as follows: the response of A-TFT on erroneous cooperation by a non-cooperative individual is cooperation instead of defection. Thus, the disadvantage of A-TFT players in the presence of defectors is about ϵc, where ϵ is the frequency of erroneous moves, and c is the cost of cooperation (for payoff values with S−P=R−T as used in our simulations, the cost of cooperation can be defined as c=P−S=T−R; Nowak & Sigmund 1994). For the spread of A-TFT, this disadvantage needs to be balanced by the benefit of (b−c)/2 (with b=T−P=R−S for payoff values as described above), as it has in groups that exclusively consist of A-TFT players where the players cooperate on average at a frequency of 0.5 (figure 2a). In a well-mixed population, the probability of an A-TFT player being in such a group is given by αⁿ⁻¹, where α is the frequency of A-TFT players. This implies that in a well-mixed, infinite population, the initial frequency that is required for a successful invasion of A-TFT in a non-cooperative population is approximately given by $\alpha ={(2ϵc/(b-c))}^{1/(n-1)}$. Thus even for a low frequency of mistakes, ϵ, and a low cost–benefit ratio, c/b, the initial frequency that is required for A-TFT to invade a non-cooperative population rapidly increases with increasing group size. In well-mixed, infinite populations, generalized reciprocity is therefore more likely to fail establish cooperation with increasing group sizes.

Figure 2.

Behavioural patterns of key strategies of generalized reciprocity. (a) A-TFT. Cooperating and defecting A-TFT players are denoted by cTFT and dTFT, respectively. Unconditional defectors are denoted by allD. In groups that consist exclusively of A-TFT players, there is no interaction that changes the number of cooperating players, except of erroneous moves. In the presence of defectors, however, there is a process that reduces the number of cooperating A-TFT players. As a consequence, A-TFT cooperates on average at a frequency of 0.5 in the absence of defectors, since erroneous moves are equally often cooperative as defective. In the presence of defectors, cooperation breaks down. (b) A-GTFT. A-GTFT players occasionally cooperate after the previous partner defected. Thus, in contrast to A-TFT, groups of A-GTFT players can correct erroneous defection. In the presence of defectors, A-GTFT players still cooperate at a high frequency. This allows defectors to invade if A-GTFT is too generous. (c) A-PAVLOV. In the presence of defectors, A-PAVLOV cooperates at an average frequency of 0.5, irrespective of the size of the group. The performance of groups that exclusively consist of A-PAVLOV players, however, becomes worse with increasing group size, because a single defecting A-PAVLOV player (dPAV) that interacts with a cooperative A-PAVLOV player (cPAV) results in two dPAV players. Thus, a single erroneous move spreads through the entire group. To run again into a state where all members of a group cooperate, the last pair of defecting dPAV need to interact and then annihilate.

However, a recent study on the evolution of reciprocal altruism (Nowak et al. 2004) indicates that in finite populations, the invasion barrier for strategies such as A-TFT, which have only a small selective disadvantage in a non-cooperative population, may be crossed by random drift. Thus in finite populations, generalized reciprocity can be expected to evolve even for high values of the initial frequency. Furthermore, in populations that are not well mixed, local reproduction and low dispersal may favour the initial spread of A-TFT, because within-group relatedness increases the fraction of groups that exclusively consist of A-TFT. Once A-TFT dominates a population, it may resist invasion by defecting strategies as long as group size is sufficiently small that the presence of a single defector has a strong effect on a group of A-TFT players. This is the case as long as the frequency of interaction between A-TFT players and a single defector in the group is much higher than the frequency of occasional mistakes, i.e. if n≪ϵ⁻¹. A-TFT is, however, vulnerable to generous strategies such as A-GTFT (figure 2b). With increasing group size, such generous strategies in turn become increasingly vulnerable to defective strategies. Additionally, the performance of A-PAVLOV decreases with increasing group size (figure 2c). This may lead to an increased cycling between, or coexistence of A-TFT, more generous strategies and defective strategies. Agent-based simulations for the invasion of A-TFT and the evolution of anonymous strategies in finite, viscous populations with local reproduction for groups with up to 10 individuals are shown in the Electronic Appendix.

5. Conclusions and discussion

In summary, our simulation results demonstrate that if individuals interact for many rounds within small groups, cooperation can evolve even if individuals cannot recognize their present partner and recall the outcome of the last encounter with them. Anonymous strategies that base their behaviour towards the present partner on the outcome of the interaction with the last partner may establish and maintain cooperation. Thus, generalized reciprocity represents an alternative mechanism for the evolution of cooperation. It has very similar strategies and remarkably similar game dynamics, but differs from direct reciprocity in that considerably less information is used as the basis for future behaviour. Furthermore, generalized reciprocity clearly differs from indirect reciprocity (Nowak & Sigmund 1998). Indirect reciprocity requires that individuals observe interactions between other individuals and base their behaviour on these observations, which requires even more specific cognitive abilities than direct reciprocity.

Although, in our simulations, pairs of individuals interact in the 2-player PD, some important aspects of our model resemble the evolution of reciprocity in the n-player iPD (Boyd & Richerson 1988), where all individuals of the group interact simultaneously. In the simplest version of the n-player iPD, as in our model, it is impossible to recognize and punish single defectors in the group. It has been reported (Boyd & Richerson 1988) that the only memory-one strategy that can stably establish and maintain cooperation is a TFT-like strategy that cooperates only if all other players cooperated in the previous round. The performance of such a strategy is similar to A-TFT in generalized reciprocity, in that a single defector in a group of TFT players leads to the breakdown of cooperation. Accordingly, our findings for the initial frequencies and stability of A-TFT are in agreement with those obtained from the n-player iPD (Boyd & Richerson 1988). However, TFT-like strategies in the n-player iPD need to estimate the number of cooperative individuals in the group. A-TFT is much simpler: it cooperates if, and only if, the last partner was cooperative. Furthermore, A-TFT allows the evolution of generous strategies and is more robust against occasional mistakes than TFT-like strategies in the n-player iPD, where a single mistake leads to the irreversible breakdown of cooperation in the group (Boyd & Richerson 1988).

Importantly, generalized reciprocity requires fewer cognitive capabilities than direct reciprocity. Thus, the evolution of cooperation by reciprocity might be possible for organisms that do not fulfil the requirements for direct reciprocity. Given that cognitive abilities such as individual recognition and memory may be associated with fitness costs (Mery & Kawecki 2002), generalized reciprocity may have advantages over direct reciprocity. Thus if cooperation is established in a population by direct reciprocity, then the strategies of direct reciprocity may degenerate to anonymous strategies. On the other hand, direct reciprocity also has benefits over generalized reciprocity, because it allows avoiding cooperation specifically towards non-cooperative group members while maintaining cooperation with cooperative group members. Thus, the outcome of competition between strategies of direct and generalized reciprocity may depend on the costs of cognitive capabilities and may be an interesting topic for further theoretical studies. Furthermore, generalized reciprocity may be used in addition to direct reciprocity. For example, direct reciprocity may be used towards known partners, while generalized reciprocity may be used in the first encounter with unknown partners.

Behaviour consistent with generalized reciprocity has been observed in humans (Berkowitz & Daniels 1964) and rats (Rutte & Taborsky submitted). On the other hand, studies primarily focusing on generalized reciprocity in sticklebacks (Milinski et al. 1990) and chimpanzees (de Waal 1997), describe behaviour that is not consistent with generalized reciprocity. To investigate the role of generalized reciprocity it appears to be essential to conduct further experimental studies, particularly on organisms with population structures that facilitate generalized reciprocity.

Appendix A

(a) Simulations for group size three

For simulating the evolution of generalized reciprocity we use population dynamical simulations analogous to those used for studying direct reciprocity (Nowak & Sigmund 1993, 1994), implying that we assume an infinite, well-mixed population, and an infinite number of noisy interactions within a group. Thus the strategies of generalized reciprocity are characterized by four probabilities (p₁, p₂, p₃, p₄) that lie between the values ϵ and 1−ϵ, where ϵ is the minimal frequency of mistakes. In our simulations, ϵ is set to 10⁻³ as in the previous simulations on direct reciprocity (Nowak & Sigmund 1993, 1994). Based on such stochastic strategies, the dynamics of the iterated game within one group corresponds to a Markov process. The stationary distribution resulting from the Markov process allows the average payoff of an individual within a group after an infinite number of iterations be computed (Nowak & Sigmund 1990). The transition matrix describing the Markov process for group size three is given below. Strategies interact with themselves and with other strategies in all possible combinations. Frequencies of strategies change according to replicator dynamics, i.e. proportionally to the ratio between the average fitness of a strategy and the average fitness of the population. For the PD, we use in our simulations the following payoff values: R=3, S=0, T=4, P=1. We start with a non-cooperative population, where all individuals use unconditional defection (allD) given by (ϵ, ϵ, ϵ, ϵ). New strategies are inserted on average once per 100 generations at an initial frequency of 3.3% in the population. Rare strategies with frequencies below 3% are removed. These values are higher than those generally used in studies of direct reciprocity (Nowak & Sigmund 1993, 1994) for reasons given in the main text (see §4). The probabilities (p₁, p₂, p₃, p₄) of new strategies are generated using a U-shaped distribution. The U-shaped distribution is generated from a uniform distribution ranging from −0.5 to 1.5. Values below 0.001 are set to 0.001, values larger than 0.999 are set to 0.999. Note that this distribution is more biased towards extreme values than the distribution typically used in direct reciprocity (Nowak & Sigmund 1993, 1994). It therefore decreases the computational time until A-TFT emerges in the population, and may favour the evolution of A-PAVLOV rather than A-GTFT. The total length of a single simulation is 2×10⁶ generations, resulting in about 2×10⁴ strategies that are tested in each run. We performed 100 replicate simulations.

(b) Calculation of payoffs

For the calculation of the payoffs we use the Markov chain formalism describing the game dynamics within a group. The three players of the group are denoted by A, B and C. The strategy of each player is characterized by four probabilities, here denoted by (a₁, a₂, a₃, a₄), (b₁, b₂, b₃, b₄) and (c₁, c₂, c₃, c₄), respectively. Each player has two options: cooperation (C), and defection (D), resulting in eight possible states for the group given by (CCC, CCD, CDC, CDD, DCC, DCD, DDC, DDD), where the letters in each triplet describe the last moves of player A, B and C, respectively. Transitions between states of the group are described by the transition matrix $M=(M_1+M_2+M_3)/3$, where M₁, M₂ and M₃ describes the state transitions for interactions between B and C, A and C, and A and B, respectively. M₁, M₂ and M₃ are related to the transition matrix for direct reciprocity between two players (Nowak & Sigmund 1994) and are given in figure 3. The stationary probability distribution is calculated numerically by iterating matrix multiplication until the distribution converges.

Figure 3.

The transition matrix describing the Markov process for group size three.