Skip to main content
PMC home page
Proceedings of the Royal Society B: Biological Sciences logoLink to Proceedings of the Royal Society B: Biological Sciences
. 2005 Jul 6;272(1572):1617–1624. doi: 10.1098/rspb.2005.3108

Pathogen adaptation under imperfect vaccination: implications for pertussis

Michiel van Boven 1,*, Frits R Mooi 2,3, Joop FP Schellekens 4, Hester E de Melker 5, Mirjam Kretzschmar 5
PMCID: PMC1559845  PMID: 16048777

Abstract

Mass vaccination campaigns have drastically reduced the burden of infectious diseases. Unfortunately, in recent years several infectious diseases have re-emerged. Pertussis poses a well-known example. Inspired by pertussis, we study, by means of an epidemic model, the population and evolutionary dynamics of a pathogen population under the pressure of vaccination. A distinction is made between infection in immunologically naive individuals (primary infection) and infection in individuals whose immune system has been primed by vaccination or infection (secondary infection). The results show that (i) vaccination with an imperfect vaccine may not succeed in reducing the infection pressure if the transmissibility of secondary infections is higher than that of primary infections; (ii) pathogen strains that are able to evade the immunity induced by vaccination can only spread if escape mutants incur no or only a modest fitness cost and (iii) the direction of evolution depends crucially on the distribution of the different types of susceptibles in the population. We discuss the implications of these results for the design and use of vaccines that provide temporary immunity.

Keywords: Bordetella, virulence, evolutionary stability, adaptive dynamics

1. Introduction

The twentieth century has witnessed the enormous success of vaccination campaigns against infectious diseases. This prompted optimism in the 1970s that a decisive victory in the battle against infectious diseases would be within reach. Alas, except for smallpox, eradication has not been achieved for any infectious disease, and in recent years the incidences of several infectious diseases show an increasing trend (see Cohen (2000) for a review).

An example of such a re-emerging infectious disease is pertussis or whooping cough. Before the introduction of mass vaccination, pertussis was one of the main causes of infant mortality, causing more deaths than all other infectious diseases of childhood taken together. Mass vaccination campaigns, started in the 1940s and 1950s, have led to a drastic reduction of the morbidity and mortality rates, and also have greatly reduced the level of circulation of Bordetella pertussis (Rohani et al. 2000). Unfortunately, in the last decade it has become clear that what was once thought to be an infectious disease under the firm control of vaccination is now a re-emerging problem in developed countries (von König et al. 2002; van Boven et al. 2004).

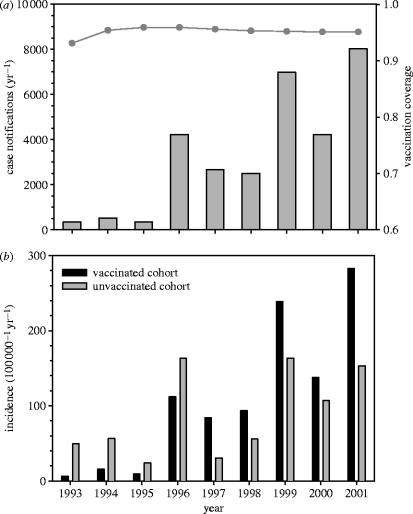
To illustrate this, figure 1 (top panel) shows the yearly number of reported cases of pertussis in the Netherlands over the years 1993–2001. The panel shows a strong increase in the number of cases since 1995. Interestingly, the increase in the number of reported cases is largely due to an increase in the incidence in vaccinated children, adolescents and adults. This is exemplified by figure 1 (bottom panel), which shows the estimated incidence in vaccinated and unvaccinated children aged 5–9 years. This panel shows that, although the incidence in unvaccinated children (ca 4% of the population) has increased considerably since 1995, the incidence in vaccinated children (ca 96% of the population) has increased much more strongly. As a result, the incidences in the vaccinated and unvaccinated cohorts are at present not significantly different.

Figure 1.

Figure 1

Open in a new tab

(a) Numbers of reported cases of pertussis in the Netherlands (grey bars), and (b) the estimated incidence of pertussis in vaccinated (grey bars) and unvaccinated (black bars) children aged 5–9 years over the years 1993–2001 (see de Melker et al. (2000) for details). Note that (a) also shows the vaccination coverage (grey line) at age 1 in infants born in the years 1993–2001.

Furthermore, the true incidence of pertussis infections may be more than an order of magnitude higher than the incidence based on notification data, as most infections in adolescents and adults are subclinical and, therefore, go unnoticed (van Boven et al. 2004 and references therein). In view of this, B. pertussis is increasingly recognized not only as an infection of infants, but also as an infection of children, adolescents and adults (e.g. Mink et al. 1992; Schmitt-Grohé et al. 1995; Wright et al. 1995; Nennig et al. 1996; Birkebaek et al. 1999; Senzilet et al. 2001; Strebel et al. 2001; Gilberg et al. 2002; see von König et al. (2002) for an overview). In fact, a recent estimate from the Netherlands suggests that the attack rate in the adult population is between 4 and 10% per year (Teunis et al. 2002).

The question arises as to why pertussis is increasing. Could this be a population dynamic phenomenon? Or is it due to changes in the pathogen population, i.e. has adaptation of the pathogen played a role? In most developed countries the composition and quality of the vaccines generally have remained constant over time, thereby excluding the possibility that the recent increases are due to defective vaccines (see van Loo et al. 1999; van Loo & Mooi 2002; von König et al. 2002; van Boven et al. 2000, 2004). It is also known that vaccines do not prevent infection for life (von König et al. 2002), and that in recent years, the fraction of infections in vaccinated individuals has increased steadily.

Recent molecular studies have resulted in a wealth of genetic data, and offer the potential to greatly improve our understanding of the genes and regulatory pathways involved in determining pathogen virulence (e.g. Smith et al. 2001; Parkhill et al. 2003). In fact, genetic studies have already revealed that populations of B. pertussis evolve by two different mechanisms. (i) The pathogen can evolve by changing its level of expression of virulence genes. As a consequence, it may become less visible to the host's immune system (in case of lowered expression) or become more efficient in colonizing the host (in case of increased expression; e.g. Cotter & DiRita 2000; Cotter & Miller 2000; Yuk et al. 2000). (ii) Polymorphisms can evolve in the epitopes of major virulence genes that hinder recognition of the pathogen by the host's immune system after vaccination (e.g. Mooi et al. 1998, 1999, 2001; van Loo et al. 1999; Cassiday et al. 2000; van Loo & Mooi 2002; Hijnen 2004).

The aim of this paper is twofold. First, we study the population dynamical consequences of mass vaccination, paying special attention to secondary infections. The population dynamical analysis sets the stage for the ensuing evolutionary analyses. We model two mechanisms of pathogen adaptation. In our first scenario, we assume that there is a trade-off between the efficiency of the pathogen in colonizing primary and secondary susceptibles, corresponding to the first evolutionary mechanism mentioned above. In the second scenario, there is a trade-off between the susceptibility of vaccinated individuals and the duration of the infectious period, corresponding to the second evolutionary mechanism mentioned above.

2. Population dynamics

How does the incidence of primary and secondary infection depend on the vaccination coverage (the fraction of the population that is vaccinated) and the transmissibility of primary and secondary infection? The epidemic model presented in figure 2 and Electronic Appendix A forms the basis of our reasoning. In a pathogen-free population, the pathogen can invade if the so-called reproduction ratio exceeds one (Diekmann & Heesterbeek 2000). The reproduction ratio is given by

Rp=(1−p)f1g1α1+μ+pσVσV+μf2g2α2+μ, 2.1

where the subscript p stresses the dependence of the reproduction ratio on the vaccination coverage (Electronic Appendix A). The critical vaccination fraction pc to achieve herd immunity is easily obtained by putting p=pc in equation (2.1) and solving the equation for Rp=1. Equation (2.1) indicates that eradication is not always feasible when vaccinating with an imperfect vaccine (McLean 1999, 2002; Gandon et al. 2003).

Figure 2.

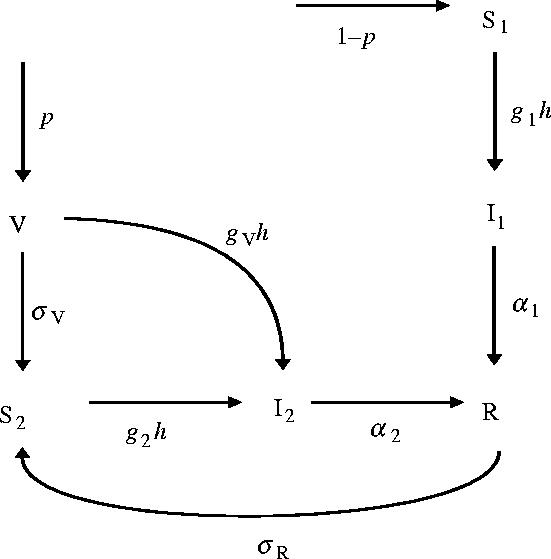
Figure 2

Open in a new tab

Model structure. Individuals are classified as primary or secondary susceptible (S1 and S2), primary or secondary infected (I1 and I2), vaccinated (V) or recovered and immune (R). Notice that we have assumed gV=0 in the population dynamical analysis.

It is possible that the reproduction ratio increases with increasing vaccination coverage. In fact, if we assume for a moment that the infectious period of primary infection equals the infectious period of secondary infection (α2=α1) this will happen if

f2g2f1g1>σV+VσV. 2.2

Hence, vaccination increases the reproduction ratio if the transmissibility of secondary infections is sufficiently higher than that of primary infections, or if secondary susceptible individuals are sufficiently more susceptible than primary susceptibles. Consequently, the reproduction ratio may be smaller than one in an unvaccinated population but higher than one in a vaccinated population (Hethcote & Li 1999; Greenhalgh et al. 2000; Medley et al. 2001).

Note that for realistic parameter values equation (2.2) may be satisfied even if primary infections are only slightly more transmissible than secondary infections. In fact, g2=g1=1, gV=0, σV=0.2 yr−1 and μ=0.013 yr−1 in the default parameter setting so that the reproduction ratio increases by vaccination if the transmissibility of secondary infections is just 7% higher than the transmissibility of primary infections.

The results of the equilibrium analyses are summarized by figure 3 (see Electronic Appendix A for details). The figure illustrates that, in general, the incidence of primary infection is much lower in a vaccinated than in an unvaccinated population. The reason is that only a small fraction of the population is available for primary infection in a vaccinated population. Figure 3 furthermore shows that the incidences of both primary and secondary infection decrease with increasing vaccination coverage if primary infections have higher transmissibility than secondary infections (i.e. f1>f2). In this case, vaccination is always beneficial because it reduces the fraction of individuals available for primary infection, as well as the infection pressure. Hence, vaccination not only has a direct protective effect to those who are vaccinated, but it also reduces the probability of infection for those who are not vaccinated.

Figure 3.

Figure 3

Open in a new tab

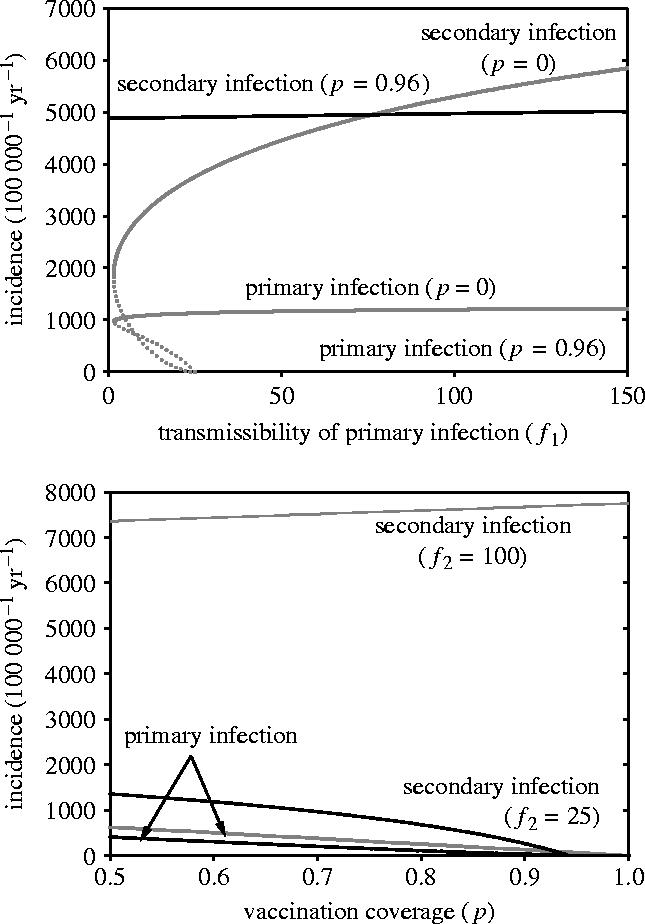
Overview of the population dynamical analysis. The top panel shows the prevalence of primary and secondary infection as a function of the infectiousness of primary infection in an unvaccinated (p=0; grey lines) and vaccinated (p=0.96; black lines) population. Stable and unstable equilibria are represented by solid and dotted lines, respectively. Parameter values are as in table 1 with f2=50. The bottom panel shows the prevalence of primary and secondary infection as a function of the vaccination coverage. Parameter values are f2=25 (black lines) or f2=100 (grey lines), with f1=50. In both panels, incidence is calculated as the prevalence at equilibrium (see Electronic Appendix A) divided by the infectious period (1/(α+μ)).

However, primary infections need not necessarily be more transmissible than secondary infections. In fact, primary infections occur most often in infants and young children, and usually lead to severe disease. This results in measures that decrease infectiousness such as isolation and antibiotic treatment. Secondary infections, on the other hand, are found mostly in adolescents and adults, and often go unnoticed. It is therefore plausible that in effect, asymptomatic secondary infections have higher transmissibility than primary infections, as secondary infected individuals will be more actively spreading the pathogen than primary infected individuals.

The consequences are profound. If secondary infections are sufficiently more transmissible than primary infections, vaccination may hamper rather than aid elimination of the pathogen. The intuitive explanation is that the effect of vaccination is to shift individuals to the class of secondary susceptibles where they are prone to highly transmissible secondary infection. As a result, vaccination may have the unpleasant consequence of increasing the infection pressure in the population. This implies that unvaccinated individuals in a vaccinated population may be at a higher risk of contracting a primary infection than individuals in an unvaccinated population. Moreover, they also may be infected at a younger age.

To give an example, let us set the transmissibility of primary and secondary infection at f1=10 yr−1 and f2=100 yr−1, and keep all other parameters at their default values (table 1). The probability that an unvaccinated individual escapes primary infection is given by μ/(h*+μ), where μ denotes the mortality rate and h* the equilibrium force of infection (e.g. Diekmann & Heesterbeek 2000). In an equilibrium state the probability of escaping infection is 4.6% in an unvaccinated population, while it is only 4.0% in a vaccinated population. The average age at primary infection is given by 1/(h*+μ). Hence, the average age at infection is 3.5 years in an unvaccinated population and 3.1 years in a vaccinated population. Since age at infection is negatively correlated with the occurrence and severity of complications (e.g. von König et al. 2002), vaccination may increase the number of primary infections with severe complications as it increases the probability of infection and decreases the age at infection.

Table 1.

Overview of the model parameters and their default values.

parameter default value description
p 0.96 vaccination coverage
μ 0.013 (yr−1) birth and death rate
σV 0.2 (yr−1) rate of loss of immunity after vaccination
σR 0.1 (yr−1) rate of loss of immunity after infection
α1 25 (yr−1) recovery rate after primary infection
α2 25 (yr−1) recovery rate after secondary infection
f1 1–250 (yr−1) transmissibility of primary infection
f2 1–250 (yr−1) transmissibility of secondary infection
g1 1 susceptibility of primary susceptibles
g2 1 susceptibility of secondary susceptibles
gV 0 susceptibility of vaccinated individuals
Open in a new tab

Notice that the parameters governing pathogen transmissibility (f1 and f2) are composite measures that incorporate both infectiousness and contact intensity.

Summarizing, although for pertussis there are undeniable benefits of mass vaccination in preventing infections with severe complications, there also is an important caveat: even in the absence of an evolutionary response by the pathogen, a vaccination campaign may not succeed in reducing the incidence of infection if the immunity conferred by vaccination is temporary and if secondary infections are in effect more transmissible than primary infections. As we have argued, this is not unlikely for pertussis.

3. Pathogen adaptation

Inspired by pertussis, we consider two different scenarios of pathogen adaptation. First, adaptation to vaccination may occur by altering the expression levels of virulence genes (adherence molecules, toxins). Second, mutations in the (epitopes of the) virulence genes may cause the bacterium to escape from the immunity in the population induced by vaccination. Figure 4 gives a schematic of the two kinds of pathogen adaptation.

Figure 4.

Figure 4

Open in a new tab

Schematic of two types of pathogen adaptation described in the text.

(a) Virulence gene expression

Will vaccination select for highly virulent pathogens that efficiently colonize and exploit unvaccinated susceptible hosts, and in doing so may cause considerable damage? Or does it select for relatively avirulent pathogens that are less efficient and do not inflict much damage? Recent theory predicts that certain types of vaccines are expected to increase virulence of the pathogen population so that unvaccinated susceptible individuals are exploited more efficiently and suffer more from the negative consequences of infection (Gandon et al. 2001). Here we ask whether similar phenomena occur if immunity against infection is temporary.

Throughout, we equate virulence with the efficiency of the pathogen to infect and exploit primary susceptibles. Hence, it is measured by the parameter f1 and it does not take into account pathogen-induced host mortality (which, on the population level, is negligible in case of pertussis in developed countries). Notice that our definition of virulence differs from definitions used in other modelling studies (e.g. van Baalen 1998; Gandon et al. 2001, 2003; Day & Burns 2003). We refer to Casadevall & Pirofski (1999) for a detailed account of the different faces and definitions of virulence.

The idea that there may be differences between strains in their ability to exploit susceptible hosts, and that there is a systematic relation between the efficiency to colonize and exploit primary and secondary susceptibles, is not hypothetical. In fact, it is conceivable that B. pertussis strains can increase their efficiency in colonizing immunologically naive hosts by an increase in the expression of surface proteins involved in adherence to host tissue (e.g. pertactin), or by an increase in the expression in the toxins involved in the suppression of the immune response of the host (e.g. pertussis toxin). At the same time, however, an increased expression of these proteins facilitates the recognition of the pathogens by the immune system of the host (Cotter & DiRita 2000; Cotter & Miller 2000; Yuk et al. 2000). In addition, the production of virulence molecules must impose an energetic cost making it unlikely that maximal expression of these genes is profitable.

Electronic Appendix B gives an outline of the analyses. In short, we have calculated the growth rates of a spectrum of mutant strains in a population in which a resident strain is present. Mutants with a positive growth rate will increase in frequency and successfully invade, while mutants with a negative growth rate cannot invade. Combinations of mutant parameter values that yield a zero growth rate represent, from an evolutionary point of view, strategies that are equivalent to the prevailing resident strategy. We focus on such strategies where the benefits of increased virulence (higher transmissibility from primary infecteds) are exactly balanced by the costs due to a lower transmissibility from secondary infecteds. The value of an increase in f1 (virulence) in terms of an evolutionarily equivalent change in f2 is given by

df2df1=−S1[f1]S2[f1], 3.1

where for simplicity we have set gV=0 (see Electronic Appendix B for general derivation). Equation (3.1) shows that the value of a change in the transmissibility of primary infection (i.e. f1) in terms of an equivalent change in the transmissibility of secondary infection (i.e. f2) is completely determined by the number of primary susceptibles per secondary susceptible in the resident population.

Figure 5 gives a graphical overview of the results. In an unvaccinated population (top panel), the value of an increase in f1 in terms of an equivalent decrease in f2 is almost independent of the transmissibility of secondary infection if the transmissibility of primary infection is high (f1=250 yr−1). The intuitive explanation is that primary susceptible individuals will be infected quickly anyway, while the distribution of primary and secondary susceptible hardly depends on the transmissibility of secondary infection. If, on the other hand, the transmissibility of primary infection is low (f1=1 yr−1), the pathogen cannot persist if the transmissibility of secondary infection drops below a certain threshold value. For values of f2 just above the threshold value the infection pressure in the population is very low and secondary susceptibles are almost absent. As a result, a small decrease in the transmissibility of primary infection f1 is equivalent to a large increase in the transmissibility of secondary infection f2.

Figure 5.

Figure 5

Open in a new tab

The evolutionary value of an increase in the infectiousness of primary infections in terms of an equivalent decrease in the infectiousness of secondary infections. The figure shows equation (3.1) as a function of the infectiousness of secondary infection. The top and bottom panels refer to an unvaccinated ( p=0) and a vaccinated ( p=0.96) population, respectively. Parameter values are as in table 1.

In a population with high vaccination coverage (figure 5, bottom panel) the value of an increase in the transmissibility of primary infection is hardly affected by the transmissibility of primary and secondary infection if the transmissibility of secondary infection is high enough (say f2>50 yr−1). Here, the intuitive explanation is that most individuals are rapidly shifted to the class of secondary susceptibles by vaccination. In this case, a certain increase in the transmissibility of primary infection is, from an evolutionary perspective, equivalent to a very small decrease in the transmissibility of secondary infection. If the transmissibility of secondary infection is very low the pathogen has difficulties persisting. As a consequence, a small increase in the transmissibility of primary infection is equivalent to a large decrease in the transmissibility of secondary infection.

To illustrate the above general results we consider a specific example. In the example, the relation between f2 and f1 is given by the following trade-off function

f2[f1]=a−bf12, 3.2

(a,b>0,0≤f1≤b/a). Using equations (3.1) and (3.2) the evolutionarily stable strategies (ESSs) can be located (Metz 1992; Dieckmann 2002; van Boven & Weissing 2004).

Figure 6 shows the relation between the vaccination coverage ( p) and the evolutionarily stable (ES) level of primary and secondary transmissibility (top panel) and the corresponding ES incidence of primary and secondary infection (bottom panel). In the figure, f1 and f2 are both able to evolve to values in the range 0–250. The top panel of figure 6 corroborates our argument that, from an evolutionary perspective, f2 is more important than f1. In fact, f2 evolves to values near its maximum while f1 evolves to low values (f1*<50). Figure 6 also shows that both the reproduction ratio and the incidence of secondary infection increase with increasing vaccination coverage, while the incidence of primary infection decreases from 1.3% per year in an unvaccinated population to 0% in a completely vaccinated population.

Figure 6.

Figure 6

Open in a new tab

The relation between the vaccination coverage and the evolutionarily stable (ES) level of primary and secondary infectiousness (top panel) and the ES level of primary and secondary infection (bottom panel). The trade-off between f2 and f1 is given by equation (3.2). Parameter values are a=1/b=250.

We conclude that whether selection favours virulent or avirulent pathogen strains depends to a large extent on the distribution of the various types of susceptible individuals in the population. Secondary susceptibles prevail for a broad range of parameter constellations. Therefore, the main selection pressure on the pathogen population will be to efficiently colonize and exploit secondary susceptibles. As a consequence, highly virulent strains that efficiently exploit primary susceptibles can only spread in the population if in doing so they are not hampered in their efficiency to infect secondary susceptibles.

(b) Immune evasion

A natural infection with B. pertussis induces long-lasting immunity in its host. As a consequence, there is a strong selection pressure on the pathogen to evade the immunity induced by prior infection. As a result, the pathogen population is expected to become highly polymorphic (May & Anderson 1983). This early theoretical prediction is corroborated by a suite of subsequent studies (Gomes et al. 2002 and references therein).

In a vaccinated population there also is selection on the pathogen to evade the immune responses elicited by the vaccine. In fact, a mutant strain that is able to infect a certain fraction of the vaccinated individuals not available to a resident strain and that is otherwise identical has a selective advantage, and can always invade. Here we explore, by means of a simple model, how differences between a resident and mutant strain affect the mutant strain's invasion prospects. Specifically, we focus on a mutant strain for which the vaccine is less effective, and we assume that individuals in the vaccinated compartment (V) can still be infected by the mutant strain. At the same time, however, the mutant strain is less fit as it induces a shorter infectious period.

A straightforward calculation (see Electronic Appendix B for methodology) shows that, at an ESS, the marginal value equation where the costs of a reduced infectious period exactly balances the benefits due to the possibility of direct infection of individuals in compartment V is given by

dαdgV=f2V[gV]=f2μμ+σV+gVh[gV]p. 3.3

Equation (3.3) shows that the success of a mutant strain is closely related to the vaccination coverage (p), the transmissibility of secondary infection (f2), and to the probability that a vaccinated individual will die before it loses its protection against infection (μ/(μ+σV+gVh[gV])). In fact, the mutant's invasion prospects increase as the vaccination coverage or the protected period after vaccination increases, because then a large fraction of the population is in compartment V.

To give an example, take the default parameter setting (table 1) with f2=50. For these parameter values the right-hand side of equation (2.1) equals 2.93 yr−1. This means that a mutant against which vaccination provides no protection at all still has to maintain an infectious period of at least (1/(25+0.013+2.93))365=13.1 days if it is to invade a population where a resident strain with infectious period of (1/(25+0.013))365=14.6 days is present. If the protected period after vaccination is 10 years instead of 5 years (σV=0.1), the mutant can invade if the infectious period is at least 11.9 days. Hence, even a mutant strain that is able to completely avoid the immunity induced by vaccination can only invade if its infectious period is only a couple of days shorter than the infectious period of the resident strain.

The empirical data on pertussis strongly suggest that vaccination has indeed selected for strains that are, to a certain extent, able to circumvent the immunity induced by vaccination (Mooi et al. 1998, 1999, 2001; van Loo et al. 1999; King et al. 2001; van Loo & Mooi 2002). For instance, the allelic variants of the pertactin and the pertussis toxin subunit 1 genes that match the Dutch vaccine were the predominant alleles in the early days of mass vaccination. Nowadays, the frequencies of these alleles have decreased to very low values, or have even disappeared altogether.

Taken together, the third message is that the invasion prospects of a rare mutant strain increase as the vaccination coverage or the period of protection after vaccination increase. However, for realistic parameter values the fitness cost of such escape mutants in terms of, for instance, a reduction in the infectious period cannot be large.

4. Discussion

We have shown that vaccination with an imperfect vaccine can have a number of counterintuitive implications. First, it may increase the level of circulation of a pathogen. As a result, elimination of the pathogen may prove more difficult in a vaccinated than in an unvaccinated population. Moreover, susceptible unvaccinated individuals in a vaccinated population may be exposed to a higher infection pressure than susceptible individuals in an unvaccinated population, thereby increasing the probability of infection and decreasing the average age at infection. Since in pertussis the age at infection is negatively correlated with the severity of disease, vaccination may increase the number of infections and complications in unvaccinated individuals.

Second, whether vaccination will select for high levels of virulence depends on the relative ability of pathogens to infect and exploit primary and secondary susceptibles. In general, a mutant pathogen strain with increased virulence (i.e. increased transmissibility of primary infection) will only successfully invade if it does not or only slightly reduces the transmissibility of secondary infection. The intuitive reason is that in a vaccinated population primary susceptibles constitute only a small fraction of the total host population (less than 5% in The Netherlands) while secondary susceptibles abound. Hence, the main selection pressure on the pathogen population will be to efficiently infect and exploit secondary susceptibles.

Third, the pathogen population may adapt to circumvent the immune responses elicited by the vaccine. In fact, mutant strains that are able to evade the immunity induced by vaccination or infection are selectively favoured. Hence, one could anticipate that the pathogen population will evolve to become highly polymorphic. However, this conclusion rests on the assumption that such mutant strains are intrinsically equally fit, or almost as fit as the resident strains. The fact that B. pertussis populations are relatively clonal could thus be taken as prima facie evidence that fitness differences between strains are not negligible. Alternatively, it could also indicate that population bottlenecks are common.

The fact that populations of B. pertussis may have evolved to circumvent the immune responses elicited by vaccination and to alter their virulence levels raises a number of questions concerning the design and use of future vaccines: which combination of antigens protects optimally against the circulating strains? How should one balance the breadth against the depth of a vaccine, i.e. should one include many polymorphic antigens or only a few monomorphic ones? Which vaccines, vaccination schemes and coverages minimize the probability of appearance of escape mutants? How does the evolutionary pressure on the pathogen population depend on the relationship between natural and vaccine-induced immunity? Should the aim of vaccination be to reduce symptomatic disease while maintaining circulation, or should it be to reduce virulence? Will vaccination select for aggressive virulent strains that efficiently exploit the host, or does it select for stealthy avirulent strains that are less visible to the immune system?

Recent transitions from whole-cell vaccines comprising tens or perhaps even hundreds of antigens to subunit vaccines comprising far fewer antigens (one to five in the case of pertussis) have made the above questions pressing. Nevertheless, up to now, vaccine effectiveness studies almost invariably have focused on short-term effects in individual persons (immune responses, side-effects; e.g. Jefferson et al. 2003). However, these studies cannot provide insight into the effect of vaccination on the level of circulation in the population, and into the long-term effects of vaccination. In view of our model results and the experimental evidence on pathogen adaptation, we believe that the design of vaccines should not only be focused on short-term individual responses, but it should take into account and anticipate the population dynamical and evolutionary consequences of vaccination as well.

Acknowledgments

Sabine de Greeff is gratefully acknowledged for providing the data of figure 1. The constructive comments of Ido Pen and two anonymous reviewers are highly appreciated.

Supplementary Material

rspb20053108s06.pdf (89.2KB, pdf)

References

  1. Birkebaek N.H, Kristiansen M, Seefeldt T, Degn J, Moller A, Heron I, Andersen P.L, Moller J.K, Ostergard L. Bordetella pertussis and chronic cough in adults. Clin. Infect. Dis. 1999;29:1239–1242. doi: 10.1086/313448. [DOI] [PubMed] [Google Scholar]
  2. Casadevall A, Pirofsky L. Host–pathogen interactions: redefining the basic concepts of virulence and pathogenicity. Infect. Immun. 1999;67:3701–3713. doi: 10.1128/iai.67.8.3703-3713.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Cassiday P, Sanden G, Heuvelman K, Mooi F, Bisgard K.M, Popovic T. Polymorphism in Bordetella pertussis pertactin and pertussis toxin virulence factors in the United States, 1935–1999. J. Infect. Dis. 2000;182:1402–1408. doi: 10.1086/315881. [DOI] [PubMed] [Google Scholar]
  4. Cohen M.L. Changing patterns of infectious disease. Nature. 2000;406:762–767. doi: 10.1038/35021206. [DOI] [PubMed] [Google Scholar]
  5. Cotter P.A, DiRita V.J. Bacterial virulence gene regulation: an evolutionary perspective. Annu. Rev. Microbiol. 2000;54:519–565. doi: 10.1146/annurev.micro.54.1.519. [DOI] [PubMed] [Google Scholar]
  6. Cotter P.A, Miller J.F. Genetic analysis of the Bordetella infectious cycle. Immunopharmacology. 2000;48:253–255. doi: 10.1016/s0162-3109(00)00237-x. [DOI] [PubMed] [Google Scholar]
  7. Day T, Burns J.G. A consideration of patterns of virulence arising from host–parasite coevolution. Evolution. 2003;57:671–676. doi: 10.1111/j.0014-3820.2003.tb01558.x. [DOI] [PubMed] [Google Scholar]
  8. de Melker H.E, Schellekens J.F, Neppelenbroek S.E, Mooi F.R, Rumke H.C, Conyn-van Spaendonck M.A. Reemergence of pertussis in the highly vaccinated population of The Netherlands: observations on surveillance data. Emerging Infect. Dis. 2000;6:348–357. doi: 10.3201/eid0604.000404. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Dieckmann U. Adaptive dynamics of pathogen–host interactions. In: Dieckmann U, et al., editors. Pursuit of virulence management: adaptive dynamics of infectious diseases. Cambridge University Press; Cambridge: 2002. pp. 39–59. [Google Scholar]
  10. Diekmann O, Heesterbeek J.A.P.Mathematical epidemiology of infectious diseases. Model building, analysis and interpretation2000Wiley; New York [Google Scholar]
  11. Gandon S, Mackinnon M.J, Nee S, Read A.F. Imperfect vaccines and the evolution of pathogen virulence. Nature. 2001;414:751–756. doi: 10.1038/414751a. [DOI] [PubMed] [Google Scholar]
  12. Gandon S, Mackinnon M, Nee S, Read A. Imperfect vaccines: some epidemiological and evolutionary consequences. Proc. R. Soc. B. 2003;270:1129–1136. doi: 10.1098/rspb.2003.2370. 10.1098/rspb.2003.2370 [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Gilberg S, Njamkepo E, Du Chatelet I.P, Partouche H, Gueirard P, Ghasarossian C, Schlumberger M, Guiso N. Evidence of Bordetella pertussis infection in adults presenting with persistent cough in a French area with very high whole-cell vaccine coverage. J. Infect. Dis. 2002;186:415–418. doi: 10.1086/341511. [DOI] [PubMed] [Google Scholar]
  14. Gomes M.G.M, Medley G.F, Nokes D.J. On the determinants of population structure in antigenically diverse pathogens. Proc. R. Soc. B. 2002;269:227–233. doi: 10.1098/rspb.2001.1869. 10.1098/rspb.2001.1869 [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Greenhalgh D, Diekmann O, de Jong M.C. Subcritical endemic steady states in mathematical models for animal infections with incomplete immunity. Math. Biosci. 2000;165:1–25. doi: 10.1016/s0025-5564(00)00012-2. [DOI] [PubMed] [Google Scholar]
  16. Hethcote H.W, Li Y. Hopf bifurcation in models for pertussis epidemiology. Math. Comput. Model. 1999;30:29–45. [Google Scholar]
  17. Hijnen M, Mooi F.R, van Gageldonk P.G, Hoogerhout P, King A.J, Berbers G.A. Epitope structure of the Bordetella pertussis protein P.69 pertactin, a major vaccine component and protective antigen. Infect. Immun. 2004;72:3716–3723. doi: 10.1128/IAI.72.7.3716-3723.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Jefferson T, Rudin M, DiPietrantonj C. Systematic review of the effects of pertussis vaccines in children. Vaccine. 2003;21:2003–2014. doi: 10.1016/s0264-410x(02)00770-3. [DOI] [PubMed] [Google Scholar]
  19. King A, Berbers G, van Oirschot H.F, Hoogerhout P, Knipping K, Mooi F.R. Role of the polymorphic region 1 of the Bordetella pertussis protein pertactin in immunity. Microbiology. 2001;147:2885–2895. doi: 10.1099/00221287-147-11-2885. [DOI] [PubMed] [Google Scholar]
  20. May R.M, Anderson R.M. Parasite–host coevolution. In: Futuyma D, Slatkin M, editors. Coevolution. Sinauer; Sunderland, MA: 1983. pp. 186–206. [Google Scholar]
  21. McLean A.R. Development and use of vaccines against evolving pathogens: vaccine design. In: Stearns S.C, editor. Evolution in health and disease. Oxford University Press; Oxford: 1999. pp. 138–151. [Google Scholar]
  22. McLean A.R. Evolution of vaccine-resistant strains of infectious agents. In: Dieckmann U, editor. Pursuit of virulence management: adaptive dynamics of infectious diseases. Cambridge University Press; Cambridge: 2002. pp. 339–361. [Google Scholar]
  23. Medley G.F, Lindop N.A, Edmunds W.J, Nokes D.J. Hepatitis-B virus endemicity: heterogeneity, catastrophic dynamics and control. Nat. Med. 2001;7:619–624. doi: 10.1038/87953. [DOI] [PubMed] [Google Scholar]
  24. Metz J.A, Nisbet R.M, Geritz S.A. How should we define ‘fitness’ for general ecological scenarios? Trends Ecol. Evol. 1992;7:198–202. doi: 10.1016/0169-5347(92)90073-K. [DOI] [PubMed] [Google Scholar]
  25. Mink C.M, Cherry J.D, Christenson P, Lewis K, Pineda E, Shlian D, Dawson J.A, Blumberg D.A. A search for Bordetella pertussis infection in university students. Clin. Infect. Dis. 1992;14:447–464. doi: 10.1093/clinids/14.2.464. [DOI] [PubMed] [Google Scholar]
  26. Mooi F.R, van Oirschot H, Heuvelman K, van der Heide H.G, Gaastra W, Willems R.J. Polymorphism in the Bordetella pertussis virulence factors P.69/pertactin and pertussis toxin in The Netherlands: temporal trends and evidence for vaccine-driven evolution. Infect. Immun. 1998;66:670–675. doi: 10.1128/iai.66.2.670-675.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Mooi F.R, He Q, van Oirschot H, Mertsola J. Variation in the Bordetella pertussis virulence factors pertussis toxin and pertactin in vaccine strains and clinical isolates in Finland. Infect. Immun. 1999;67:3133–3134. doi: 10.1128/iai.67.6.3133-3134.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Mooi F.R, van Loo I.H, King A.J. Adaptation of Bordetella pertussis to vaccination: a cause for its reemergence? Emerging Infect. Dis. 2001;7:526–528. doi: 10.3201/eid0707.017708. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Nennig M.E, Shinefield H.R, Edwards K.M, Black S.B, Fireman B.H. Prevalence and incidence of adult pertussis in an urban population. JAMA. 1996;275:1672–1674. [PubMed] [Google Scholar]
  30. Parkhill J, et al. Comparative analysis of the genome sequences of Bordetella pertussis, Bordetella parapertussis and Bordetella bronchiseptica. Nat. Genet. 2003;35:32–40. doi: 10.1038/ng1227. [DOI] [PubMed] [Google Scholar]
  31. Rohani P, Earn D.J, Grenfell B.T. Impact of vaccination on pertussis transmission in England and Wales. Lancet. 2000;355:285–286. doi: 10.1016/S0140-6736(99)04482-7. [DOI] [PubMed] [Google Scholar]
  32. Schmitt-Grohé S, Cherry J.D, Heininger U, Uberall M.A, Pineda E, Stehr K. Pertussis in German adults. Clin. Infect. Dis. 1995;21:860–866. doi: 10.1093/clinids/21.4.860. [DOI] [PubMed] [Google Scholar]
  33. Senzilet L.D, Halperin S.A, Spika J.S, Alagaratnam M, Morris A, Smith B. Pertussis is a frequent cause of prolonged cough illness in adults and adolescents. Clin. Infect. Dis. 2001;32:1691–1697. doi: 10.1086/320754. [DOI] [PubMed] [Google Scholar]
  34. Smith A.M, Guzman C.A, Walker M.J. The virulence factors of Bordetella pertussis: a matter of control. FEMS Microbiol. Rev. 2001;25:309–333. doi: 10.1111/j.1574-6976.2001.tb00580.x. [DOI] [PubMed] [Google Scholar]
  35. Strebel P, Nordin J, Edwards K, Hunt J, Besser J, Burns S, Amundson G, Baughman A, Wattigney W. Population-based incidence of pertussis among adolescents and adults, Minnesota, 1995–1996. J. Infect. Dis. 2001;183:1353–1359. doi: 10.1086/319853. [DOI] [PubMed] [Google Scholar]
  36. Teunis P.F, van der Heijden O.G, de Melker H.E, Schellekens J.F, Versteegh F.G, Kretzschmar M.E. Kinetics of IgG-antibody response to pertussis toxin after infection with B. pertussis. Epidemiol. Infect. 2002;129:479–489. doi: 10.1017/s0950268802007896. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. van Baalen M. Coevolution of recovery ability and virulence. Proc. R. Soc. B. 1998;265:317–325. doi: 10.1098/rspb.1998.0298. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. van Boven M, Weissing F.J. The evolutionary economics of immunity. Am. Nat. 2004;163:277–294. doi: 10.1086/381407. [DOI] [PubMed] [Google Scholar]
  39. van Boven M, de Melker H.E, Schellekens J.F, Kretzschmar M. Waning immunity and subclinical infection in an epidemic model: implications for pertussis in the Netherlands. Math. Biosci. 2000;164:161–182. doi: 10.1016/s0025-5564(00)00009-2. [DOI] [PubMed] [Google Scholar]
  40. van Boven M, Ferguson N.M, van Rie A. Unveiling the burden of pertussis. Trends Microbiol. 2004;12:116–119. doi: 10.1016/j.tim.2004.01.002. [DOI] [PubMed] [Google Scholar]
  41. van Loo I.H, van der Heide H.G, Nagelkerke N.J, Verhoef J, Mooi F.R. Temporal trends in the population structure of Bordetella pertussis during 1949–1996 in a highly vaccinated population. J. Infect. Dis. 1999;179:915–923. doi: 10.1086/314690. [DOI] [PubMed] [Google Scholar]
  42. van Loo I.H, Mooi F.R. Changes in the Dutch Bordetella pertussis population in the first 20 years after the introduction of whole-cell vaccines. Microbiology. 2002;148:2011–2018. doi: 10.1099/00221287-148-7-2011. [DOI] [PubMed] [Google Scholar]
  43. von König C.H, Halperin S, Riffelmann M, Guiso N. Pertussis of adults and infants. Lancet Infect. Dis. 2002;2:744–750. doi: 10.1016/s1473-3099(02)00452-8. [DOI] [PubMed] [Google Scholar]
  44. Wright S.W. Pertussis infections in adults with persistent cough. JAMA. 1995;273:1044–1046. [PubMed] [Google Scholar]
  45. Yuk M.H, Harvill E.T, Cotter P.A, Miller J.F. Modulation of host immune responses, induction of apoptosis and inhibition of NF-κB activation by the Bordetella type III secretion system. Mol. Microbiol. 2000;35:991–1004. doi: 10.1046/j.1365-2958.2000.01785.x. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

rspb20053108s06.pdf (89.2KB, pdf)

Articles from Proceedings of the Royal Society B: Biological Sciences are provided here courtesy of The Royal Society

RESOURCES