Population effects of increased climate variation

Abstract

Global circulation models predict and numerous observations confirm that anthropogenic climate change has altered high-frequency climate variability. However, it is not yet well understood how changing patterns of environmental variation will affect wildlife population dynamics and other ecological processes. Theory predicts that a population's long-run growth rate is diminished and the chance of population extinction is increased as environmental variation increases. This results from the fact that population growth is a multiplicative process and that long-run population growth rate is the geometric mean of growth rates over time, which is always less than the arithmetic mean. However, when population growth rates for unstructured populations are related nonlinearly to environmental drivers, increasing environmental variation can increase a population's long-run growth rate. This suggests that patterns of environmental variation associated with different aspects of climate change may affect population dynamics in different ways. Specifically, increasing variation in rainfall might result in diminished long-run growth rates for many animal species while increasing variation in temperature might result in increased long-run growth rates. While the effect of rainfall is theoretically well understood and supported by data, the hypothesized effect of temperature is not. Here, I analyse two datasets to study the effect of fluctuating temperatures on growth rates of zooplankton. Results are consistent with the prediction that fluctuating temperatures should increase long-run growth rates and the frequency of extreme demographic events.

1. Introduction

Anthropogenic modification of the biosphere is projected to result in increased variability in precipitation and diminished variability but more frequent extreme temperatures (Karl et al. 1995; Groisman et al. 1999; Easterling et al. 2000). Empirical evidence supporting these predictions is quickly accumulating (Karl et al. 1995; Easterling et al. 2000). In contrast to the effects of changing average environmental conditions, like global warming (Schneider & Root 2002; Nemani et al. 2003; Verburg et al. 2003), the effects of increasing climate variability on biological populations are poorly understood (Fang et al. 2001; Knapp & Smith 2001; Knapp et al. 2002; McLauglin et al. 2002; Weltzin et al. 2003).

Population growth rate is the central unifying concept of population dynamics (Sibly & Hone 2002; Lewontin 2003), linking together all aspects of density dependence, resource dependence, and interspecific and intraspecific interactions like competition, predation, mutualism, cannibalism and cooperation (Sibly & Hone 2002). Represented by the parameter λ, population growth rate relates the abundance of individuals in an unstructured population at two times t and t+τ by the fundamental equation (Royama 1977)

$$N_{t+\tau }=\lambda N_t.$$ 1.1

Though simple, this model is useful for illustrating the key idea of this paper: that how environmental variation affects average population growth rates depends on individual species' physiological ecologies. In general, λ is a function of numerous features of the population's environment, including the abundance of the population, the abundance of other species and abiotic features of the environment. In a randomly fluctuating environment, λ is a random variable. The long-run growth rate of the population, the rate at which almost every population will eventually grow, is given by the geometric mean of the individual realizations of λ, λ_G=(Πλ_i)^1/k, for k+1 censuses (Lewontin & Cohen 1969; Lande et al. 2003). The fact that the arithmetic mean of λ, λ_A=(1/k)Σλ_i, is always greater than or equal to its geometric mean has been interpreted to imply that increasing environmental variability, such as results from anthropogenic climate change, will result in a decrease in long-run population growth rates (Lewontin & Cohen 1969; Efford 2001; Lande et al. 2003). This perspective does not consider how environmental variability is transmitted to a population's growth rate (Higgins et al. 2000; Davis et al. 2002).

When variability is transmitted to population growth rate through a mediating environmental variable such as temperature or rainfall, represented by ξ, the effect of increasing the variance of ξ will depend on the shape of the functional dependence of λ on ξ (Royama 1977; Davis et al. 2002). If λ(ξ) is convex, Jensen's inequality ensures that λ_A will increase with increasing variance in ξ, while λ_A will decrease with increasing variance in ξ if λ(ξ) is concave (Ruel & Ayres 1999; Pásztor & Kisdi 2000). If λ(ξ) is linear, λ_A will not change with increasing variance in ξ. Finally, if λ(ξ) has an inflection point somewhere in its range so that it is convex over some interval and concave over another interval, then the effect of increasing variance in ξ on λ_A will depend on the distribution of ξ. Thus, because λ_G≤λ_A, the well known effect that increasing variance in ξ diminishes λ_G is only ensured when λ(ξ) is concave or linear. Where λ(ξ) is convex, the effect of increasing variance in ξ on λ_G is inconsistent in the sense that it can either increase or decrease (or, as an unlikely borderline case, have no effect). A sufficient condition for λ_G to increase with increasing variance in ξ is for λ(ξ) to be increasing and log-convex (Cohen 1980).

Global circulation models suggest and empirical observations confirm that anthropogenic climate change has resulted in increased variation in precipitation and might cause increased variation in temperature (Easterling et al. 2000). Increased variability in these two environmental factors may have very different effects on biological populations. The relationship between population growth rate and the availability of a resource, which is sometimes called numerical response (Turchin 2003), is a saturating (concave) function for numerous consumer-resource systems (Sibly & Hone 2002; Turchin 2003). Thus, when rainfall has a direct effect on a resource, such as forage for herbivores, the effect of increasing variability in rainfall will be to decrease both the average population growth rate of the herbivore population and the long-run population growth rate. In contrast, metabolic theory, Arrhenius's equation in particular, predicts that individual development and resulting population growth rates will be at least an exponential function of temperature for birds and virtually all exotherms (Gillooly et al. 2002; Huntley & Lopez 1992). This prediction is supported by data collected for numerous species from a range of ecosystems (Gillooly & Dodson 2000; Huntley & Lopez 1992). Thus, increasing variability in temperature might result in increasing long-run growth rates through infrequent realization of extremely high growth rates.

The effects of fluctuations in resources and resource limitation are well known to be ubiquitous (Berryman 2004; White 2004). Here, I bring together two lines of evidence that support the hypothesis that increasing variation in temperature might result in increased long-run population growth rate. First, I analysed a dataset collected by Huntley & Lopez (1992) on the effect of controlled incubation temperature on generation time in zooplankton. Second, I examined long-term time-series of zooplankton abundance in a temperate lake to determine if extremely high and low population growth rates are more likely to occur in years when water temperature is more variable. The results of both analyses are consistent with the hypothesis that increased variation in temperature will result in higher long-run growth rates.

2. Material and Methods

(a) Effect of water temperature on generation time in zooplankton

To examine whether or not population growth rates might be a log-convex function of temperature, I examined the dataset compiled by Huntley & Lopez (1992; their appendix A) relating generation time, individual growth rate and temperature for 33 species of copepods studied under controlled conditions. For species with overlapping generations, the population growth rate (λ) is related to generation time (η) through the concept of the intrinsic rate of increase (r), according to

$$r={\eta }^{-1}={\text{log}}_{\text{e}}(N_{t+\tau }/N_t)={\text{log}}_{\text{e}}(\lambda ).$$ 2.1

If λ(ξ) was exponential, the plot of η⁻¹ versus temperature would be linear. I determined if a linear or exponential model better explained variation in generation time by fitting a generalized linear model for the relationship between η⁻¹ and water temperature using identity and log link functions and comparing Akaike's information criterion (AIC) scores for model fit (McCullough & Nelder 1989).

(b) Frequency of extreme demographic events in zooplankton

To test if variation in water temperature at current levels has an effect on population growth rates, I obtained data on the population dynamics of zooplankton in Trout Lake, Wisconsin, USA. The North Temperate Lakes Long Term Ecological Research data catalogue (http://limnosun.limnology.wisc.edu/) was accessed on 16 September 2004 to obtain a multi-species time-series of plankton density and water temperature for Trout Lake, Wisconsin, USA (89°40′ W, 46°02′ N) for approximately 23 years, beginning in April 1981. Zooplankton data from the dataset ‘North Temperate Lakes LTER: Zooplankton—Trout Lake Area’ represent the density of each species reported as number per litre. Samples were collected biweekly when the lake was ice-free and every six weeks, otherwise. Additional metadata are available from the LTER web site.

These raw data were filtered so that only species with greater than 100 recorded observations in 23 years were retained. Pseudospecies that represent groups larger than a single species were also eliminated (i.e. copepod nauplii), resulting in time-series of 11 species for analysis: Diacyclops thomasi, Filinia terminalis, Gastropus stylifer, Kellicottia longispina, Keratella cochlearis, Keratella crassa, Keratella earlinae, Keratella quadrata, Polyarthra remata, Polyarthra vulgaris and Tropocyclops extensus. Each of these was observed in at least 19 of 23 years and six species were observed in all 23 years. Estimates of the average growth rate between consecutive observations were obtained from the standard formulae $\hat{r}={\log }_{\text{e}}(N_{t+\tau }/N_t)/\tau$ and $\hat{\lambda }=e^{\hat{r}}$, where N_t and N_t+τ are subsequent observations of a species in the dataset (sometimes, but not necessarily, on subsequent sampling dates) and τ is the time lag in days between subsequent observations.

Water temperature data from the dataset ‘Physical Limnology of the North Temperate Lakes Primary Study Lakes’ were obtained for the same period. Water temperature measurements from various depths were averaged to obtain a depth-averaged estimate for each observation date. I then computed the mean and standard deviation of depth-averaged water temperature in a year to use as predictors of growth rate. I used linear regression to confirm that there was no evidence for a trend in the mean or standard deviation of depth-averaged water temperature over time (mean: p=0.560; s.d.: p=0.822).

For each year and species, I identified the minimum and maximum values of λ as indicators of the frequency and severity of extreme demographic events. To test for effects of variation on growth parameters for each species for each year, I fitted a repeated measures general linear model using species as the subject and standard deviation in water temperature as an effect. Mean water temperature was included as a covariate as it is known to have an effect on generation time (Huntley & Lopez 1992; Gillooly 2000; Gillooly & Dodson 2000).

3. Results

(a) Effect of water temperature on generation time

The dependence of η⁻¹ on water temperature is approximately exponential (figure 1), implying that the relationship between λ and temperature is log-convex. Fitting generalized linear models with identity and log link functions confirms this impression. The AIC difference is Δ_AIC=115, providing overwhelming support for the exponential model against the linear model (Burnham & Anderson 2002).

Figure 1.

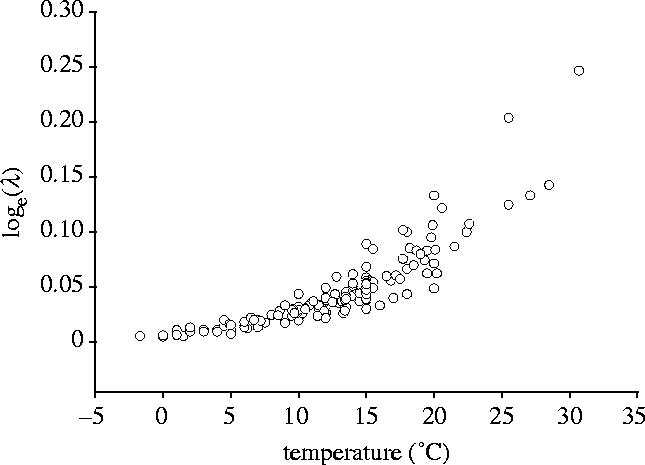
The natural logarithm of population growth rate (λ) is an exponential function of temperature for 33 species of copepods, implying that the relationship between λ and temperature is log-convex.

(b) Frequency of extreme demographic events

Standard deviation and mean depth-averaged water temperature were positively associated with λ_max (p<0.001 and p=0.050, respectively). Similarly, standard deviation in depth-averaged water temperature was negatively associated with λ_min (p<0.001), while mean depth-averaged water temperature was negatively associated with λ_min, though this result is marginally insignificant (p=0.069). There was no evidence that standard deviation and mean depth-average water temperature were correlated with each other (Pearson's ρ=0.065, p=0.309). These results imply that as variation in water temperature increases, extreme values of λ at both ends of the range are more likely to occur (figure 2). Whether the severity of observed extreme demographic events is a direct causal effect of environmental variation or is due to covariation with an unknown factor cannot be determined from these data.

Figure 2.

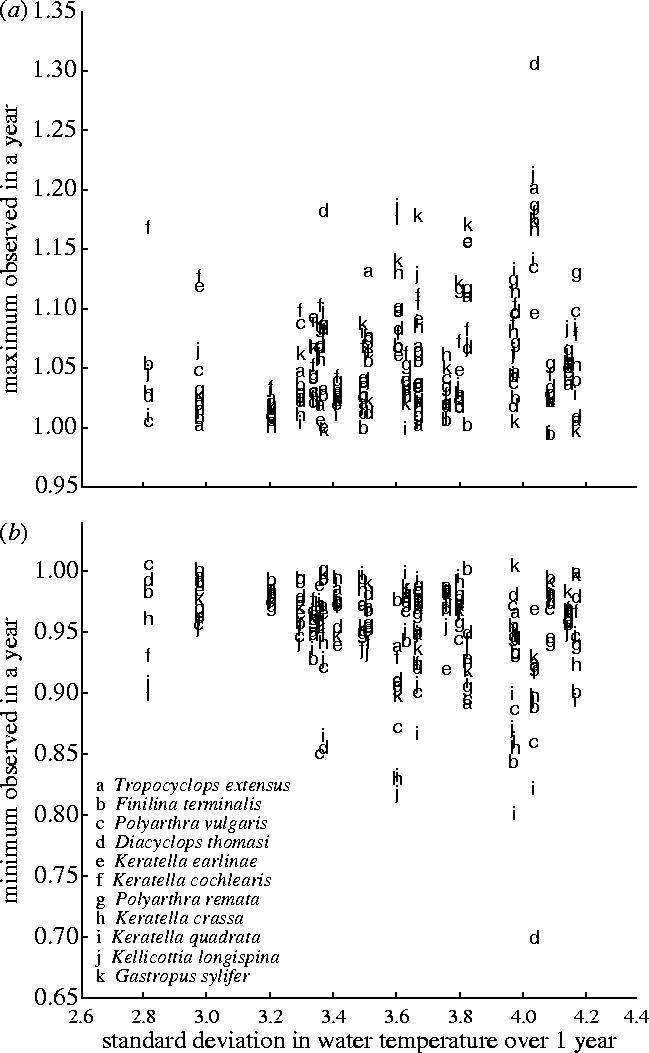
Maximum estimated values of λ in a year were positively associated with variability in water temperature for 11 plankton species (p<0.001), while minimum estimated values of λ were negatively associated (p<0.001). The effect of mean water temperature was treated as a covariate to control for known effects.

4. Discussion

These results imply that the increase in extreme weather events resulting from climate change might cause extreme demographic events that could either increase or decrease long-run population growth rates, depending on how environmental variability is translated into demography. Specifically, increasing variation in rainfall is expected to diminish the long-run growth rate of populations that are dependent on precipitation driven resources, such as herbivores, because the numerical responses of these species are typically concave (Davis et al. 2002; Sibly & Hone 2002). In contrast, as a result of Arrhenius's equation, which describes the effect of temperature on the rate of a chemical reaction, increasing environmental variability might increase the long-run population growth rate of populations whose instantaneous growth rates are determined by temperature in a direct way, such as plankton and most other exotherms (Gillooly & Dodson 2000). Two independent lines of evidence confirm this prediction. First, analysis of the experimental data compiled by Huntley & Lopez (1992) indicates that the relationship between population growth rate and temperature is log-convex in copepods. Second, analysis of long-term plankton data confirmed that extreme demographic events—observations of growth rate over short time-scales that fall within the tails of the distribution—are associated with variability in temperature.

That vital rates often depend nonlinearly on temperature is known to the large empirical literature on temperature dependent rates of development (Joshi 1996) and developmental norms of reaction (genetic×environment effect on phenotype; Brakefield & Kesbeke 1997), particularly in entomology (Beck 1983; Ayres & Scriber 1994; Joshi 1996). I am unaware, however, of previous efforts to understand how fluctuations in temperature resulting from anthropogenic climate change will affect population dynamics.

The finding reported here, that environmental variation can increase population growth rates under some conditions, is not entirely unprecedented. Recently, Levine & Rees (2004) showed that environmental variation can increase the fitness of an inferior competitor in simulated mixed forb–grass communities. Additionally, results derived by Cohen (1980) imply that the long-run growth rate of a strictly age-structured population is a log-convex function of ξ when each vital rate (survivorship or fecundity) is itself a log-convex function of ξ. The extension of these ideas to models for stage-structured and density-dependent population growth (along the lines of Turelli 1977; Royama 1977; Tier & Hanson 1981; Tuljapurkar 1990), and growth of populations with more realistic, and mixed functions for the relationship between environmental drivers and vital rates awaits development. Meanwhile, it is evident that increasing variation in climate need not necessarily diminish population growth rates, as has been conventionally supposed, but rather that effects will depend on the population and metabolic processes that relate the realized growth rates of a population to its environment.