Skip to main content
PMC home page
Proceedings of the Royal Society B: Biological Sciences logoLink to Proceedings of the Royal Society B: Biological Sciences
. 2005 Jul 26;272(1574):1769–1773. doi: 10.1098/rspb.2005.3133

Terror birds on the run: a mechanical model to estimate its maximum running speed

R Ernesto Blanco 1,*, Washington W Jones 2
PMCID: PMC1559870  PMID: 16096087

Abstract

‘Terror bird’ is a common name for the family Phorusrhacidae. These large terrestrial birds were probably the dominant carnivores on the South American continent from the Middle Palaeocene to the Pliocene–Pleistocene limit. Here we use a mechanical model based on tibiotarsal strength to estimate maximum running speeds of three species of terror birds: Mesembriornis milneedwardsi, Patagornis marshi and a specimen of Phorusrhacinae gen. The model is proved on three living large terrestrial bird species. On the basis of the tibiotarsal strength we propose that Mesembriornis could have used its legs to break long bones and access their marrow.

Keywords: palaeobiology, phororhacids, biomechanics, maximum running speed

1. Introduction

The phororhacids, which consists of five subfamilies and 13 genera (Alvarenga & Höfling 2003), were large terrestrial birds that thrived in the ecosystems of the American continents from the Middle Palaeocene to the Pliocene–Pleistocene limit. Most of the fossil record of these birds has been found in South America, but includes also a species of the late Pliocene of North America, Titanis walleri with more than 300 kg (Baskin 1995). It was commonly accepted among palaeontologists that T. walleri was the most recent species, until the finding of a tibiotarsus in San José (Uruguay), dated as Pliocene—Early Pleistocene (Tambussi et al. 1999).

There is a general agreement regarding the terror birds inability to fly. They had to rely on legged terrestrial locomotion. Anatomical similarities with living Cariamidae and Sagittaridae families have been observed (Andrews 1899), but due to the great difference of body mass between these extant birds one cannot rely on them as an input for palaeobiological inferences. According to some authors, the extinction of this group at the beginning of the Pleistocene was provoked by the ecological displacement by placental predators coming from North America during the Great American Biotic Interchange (Marshal & Cifelli 1990; Webb 1991). Not much is known about the palaeobiology of these non-flying birds.

The maximum running speed of a species can be highly relevant to its fitness (Irschik & Garland Jr 2001). For a faster predator it is easier to surprise and confuse its victim, reducing the possibility of counter-attack. Furthermore, high speed also minimizes the time spent within the range of the prey's weaponry (Paul 1998). Many authors have proposed parameters that may be correlated with the running abilities of an animal, such as length ratios of limbs bones (Garland Jr & Janis 1993; Christiansen 2002) and bone strength (Blanco et al. 2003; Christiansen 1998). For non-avian theropods some other limiting factors have been proposed, such as risk of falling (Blanco & Mazzetta 2001; Farlow et al. 1995) and leg extensors muscle mass (Hutchinson 2004; Hutchinson & García 2002). There are studies of locomotor capabilities in birds (for example: Alexander et al. 1979; Zeffer et al. 2003). However, none of these works provide a method of estimating maximum running speeds of extinct taxa. In a recent previous work, one of us developed and tested a biomechanical model to estimate maximum running speed of extant mammals (Blanco et al. 2003). In this model the strength of the appendicular bones is the main constraint for the development of maximum speed of displacement in tetrapods with parasagital limbs. There is a good correlation between the predictions of the model and known data of extant mammals. The required osteometric information is accessible from fossil bones of many extinct species. All mammals studied in Blanco et al. (2003) have body masses above 20 kg. The main hypothesis of the model might be doubtful for smaller animals. Locomotion in large and very large mammals has been proposed to be constrained by a bone safety factor (Biewener 1990), but the general limitations for maximum speed have not been completely explored (see Biewener 1989, 1990; Farley 1997; Weyand et al. 2000; Hutchinson 2004). However, the good fit between the predictions of the model and the observed values for large mammals suggests that the main assumption may be valid for the range of body size given in Blanco et al. (2003). In the present work we calculate the maximum running speed of three species of South American terror birds: Mesembriornis milneedwardsi (70 kg; see figure 1), Patagornis marshi (45 kg) and a specimen of Phorusrhacinae gen. (350 kg; see figure 2). The choice of species was made to have a set representing a broad range of body size (from 40 to 350 kg) and a large span of geological time (from Early Miocene to Pliocene–Pleistocene limit). We also calculated the maximum running speed of three large ratite species (rhea, ostrich and emu) to establish the reliability of the mechanical model for birds. We leave aside smaller running birds such as phasianids and rails, because their masses are beyond the scope of the model (Blanco et al. 2003). Finally we end our discussion with the more particular case of the moa (Anomalopteryx didiformis), a giant bird from the Quaternary of New Zealand.

Figure 1.

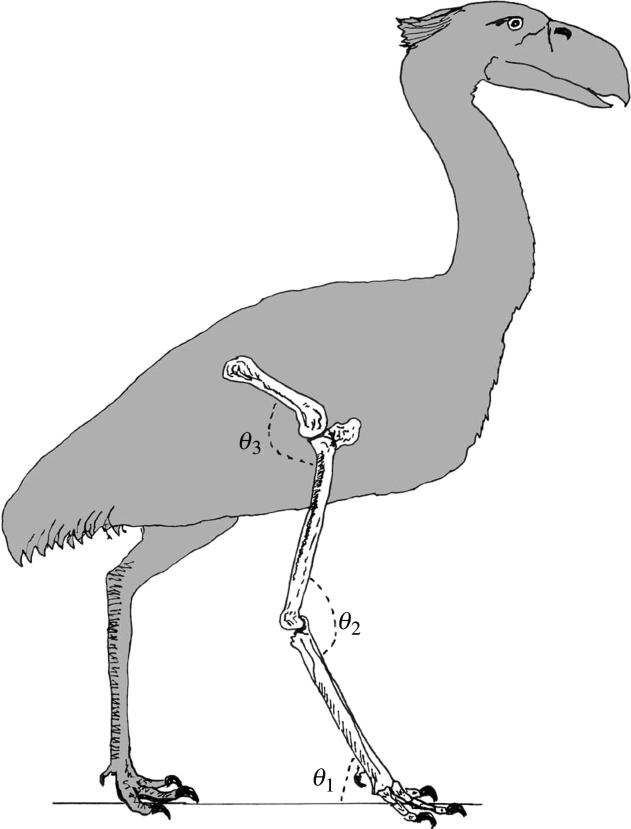
Figure 1

Open in a new tab

Silhouette of Mesembriornis milneedwardsi showing the three limb segments and the corresponding angles considered in the mechanical model (see table 3; modified from Kraglievich 1932, Pl. LVIII)

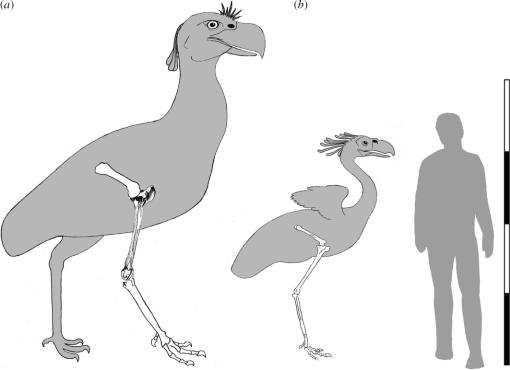
Figure 2.

Figure 2

Open in a new tab

Siluets of Phorusrhacinae gen. (a) modified from figure 1 and tibiotarsus adapted from Tambussi et al. (1999, fig. 1) and Patagornis marshi (b) modified from Andrews (1899, fig. 3) showing the three limb segments considers. Each scale bar represents 50 cm (adapted from Rinderknecht & Noriega (2002, fig. 5).

2. Material and Methods

The mechanical model is based in Blanco et al. (2003). We consider for each species the lengths of the three main segments of the hindlimbs (femur, tibiotarsus and foot segment), lever arm length of the ankle extensors, body mass, section moduli in several points of the tibia calculated from transverse and antero-posterior diameters (tables 1 and 2).

Table 1.

Input data of the model: phororhacids.

species Patagornis marshi Mesembrionis milneedwarsi Phorusrhacinae gen.
femoral length (cm) 22.7 24.1 41.2a
tibial length (cm) 39.5 42.1 72
interval of diameters and distance for the first measurement to the proximal end (cm) 3/5.4 4/4.8 6/9.6
antero–posterior diameters (mm) 28, 24, 24, 22, 20, 22, 22, 22, 22, 20, 36 72, 36, 36, 36, 36, 30, 30, 30, 54 178, 70, 54, 51, 45, 48, 38, 38, 38, 89
transverse diameters (mm) 34, 36, 33, 31, 29, 29, 28, 28, 26, 28, 37 64, 43, 43, 39, 34, 34, 34, 39, 52 96, 77, 64, 64, 57, 57, 57, 57, 70, 96
foot length (cm) 42.3 39 66.7a
lever arm (cm) 3 3.6 5.1a
body mass (kg; body mass range) (23)–45–(68) (35)–70–(105) (200)–350–(500)a
Open in a new tab

The foot length is considered from tarsometarsus segment to the more proximal phalange that makes contact with the ground. The lever arms of the ankle extensors were estimated for extinct taxa by personal observation in extant dissected birds. In parentheses are the estimated limits of body mass.

a

These values were estimated assuming geometric similarity with Mesembriornis milneedwardsi.

Table 2.

Input data of the model: the moa and extant birds.

species Anomalopteryx didiformis Struthio camelus Rhea americana Dromaius novaehollandiae
femoral length (cm) 23 30 23 20
tibial length (cm) 40.5 55 35 36
interval of diameters and distance for the first measurement to the proximal end (cm) 5/10 10/10 3/4 5/5
antero–posterior diameters (mm) 37, 27, 28, 25, 25 39, 29, 28, 28, 25 25, 22, 20, 19, 19, 19, 18, 18, 18 43, 28, 21, 19, 18, 17
transverse diameters (mm) 44, 44, 38, 38, 42 43, 36, 37, 31, 40 26, 23, 22, 23, 23, 22, 21, 21, 25 35, 27, 23, 22, 20, 21
foot length (cm) 19 60 41 40
lever arm (cm) 4.5 4 3 3
body mass (kg; body mass range) (20)–40–(60) (40)–70–(100) (20)–25–(30) (30)–40–(50)
Open in a new tab

The foot length is considered from tarsometatarsus segment to the more proximal phalange that makes contact with the ground. The lever arms of the ankle extensors were estimated for extinct taxa by personal observation in extant dissected birds. In parentheses are the estimated limits of body mass.

The bone measurements used in the present work were taken from the following sources:

Phorusrhacinae gen., tibial antero-posterior and tibial transverse diameters were measured from Tambussi et al. (1999, fig. 1).

For Mesembriornis and Patagornis other limb measurements (femoral, tibiotarsal and foot-segment lengths) and body mass estimations were taken from Alvarenga & Höfling (2003). For Phorusrhacinae gen. only the tibia is known, and for this reason other measurements were estimated assuming geometrical similarity with Mesembriornis.

For extant birds and moa, bone measurements and body masses were taken from specimens kept in the Zoological Museum of the University of Copenhagen (CN). The specimens are: ostrich, Struthio camelus CN s/n; rhea, Rhea americana CN 22; emu Dromaius novaehollandiae CN 23; moa, Anomalopteryx didiformis CN s/n.

The predicted maximum speed is very sensitive to body mass value estimates and at the same time the body mass estimate is the most uncertain. The other measurements used have a relatively small effect on the predicted maximum running speed. For error estimation we looked at error ranges of body mass, and error estimation was made following the methods described in Blanco et al. (2003).

3. Results

All the results are shown in table 3. The model predicted for ostrich a speed of 18 m s−1∼65 km h−1. The observed speed in ostrich, S. camelus, was 17 m s−1∼61 km h−1 in a female of 40 kg (Alexander et al. 1979) very close to our result. The speed predicted by the model for emu is 13 m s−1∼47 km h−1. Wild emus D. novaehollandiae have been recorded running several kilometers at speeds exceeding 14 m s−1∼50 km h−1 (Patak & Baldwin 1998), again very close to our result. The speed obtained by the model for rhea is 15 m s−1∼54 km h−1. In the literature there are no reliable records of maximum running speed for R. americana, but the zoologist Brehm wrote that some of these birds could reach the speed of a horse (Brehm 1880), i.e. consistent with our result.

Table 3.

Results.

species maximum running speed ( m s−1) limb geometry (θ1θ2θ3)* ground reaction force (body weight units)
Patagornis marshi (30)–14–(9) (61° 109° 123°) 63° 117° 134° (64° 121° 139°) (3.8)–2.3–(1.7)
Mesembriornis milneedwardsi (58)–27–(17) (61° 97° 86°) 59° 103° 108° (59° 107° 117°) (6)–3.5–(2.6)
Phorusrhacinae gen. (26)––14–(10) (60° 113° 128°) 62° 120° 137° (63° 123° 140°) (2.8)–1.8–(1.4)
Anomalopteryx didiformis (69)–31–(20) (57° 98° 70°) 55° 102° 91° (54° 104° 101°) (7.5)–4.4–(3.2)
Struthio camelus (32)–18–(12) (62° 115° 132°) 64° 121° 139° (65° 125° 143°) (3.6)–2.4–(1.8)
Rhea americana (19)–15–(12) (63° 115° 134°) 64° 118° 137° (65° 120° 139°) (2.9)–2.4–(2.1)
Dromaius novaehollandiae (17)–13–(10) (65° 120° 139°) 63° 117° 135° (64° 119° 137°) (2.7)–2.2–(1.9)
Open in a new tab

Between parentheses the results obtained for the body mass range extremities. The ground reaction force is expressed in body weight terms: body mass times gravitational constant (g=9.8 m s−2). Limb geometry: the relative positions of the bones of the foot at maximum running speed: *θ1: the angle of the foot segment with the ground; *θ2: the angle between the foot segment and the tibiotarsus; *θ3: the angle between the tibiotarsus and the femur (see figure 1).

The speed obtained for P. marshi and Phorusrhacinae gen. is 14 m s−1∼50 km h−1. For M. milneedwardsi, a speed superior to S. camelus was predicted (27 m s−1~97 km h−1). Even higher is the estimated speed of moa, A. didiformis (31 m s−1∼112 km h−1).

4. Discussion

Studies of maximum running speed in extant wild animals are still lacking accuracy and broad sample studies. Many published speeds are estimates, based on speedometer readings of a vehicle driving alongside the running animal. These are highly unreliable. For example, in the case of the fastest terrestrial tetrapod, the cheetah, there is only one record published for a tamed specimen (Alexander 2003). Leaving aside these difficulties the model explained very satisfactorily the maximum speed observed in mammals (Blanco et al. 2003) and the living birds modelled by us.

The speeds obtained for P. marshi and Phorusrhacinae gen. (14 m s−1∼50 km h−1) are as fast as several large extant mammalian carnivores. According to a study on the running capabilities in bipeds and the leg extensor muscles mass, the increment of the body size implies a decline in the running speed (Hutchinson 2004). With this assumption, the estimated speed for the huge Phorursrhacinae gen. seems doubtful. However, the phororhacid group could have an apomorphically large extensor muscles like the fast running extant ratites (Hutchinson 2004). For M. milneedwardsi, an extremely high speed was predicted (27 m s−1∼97 km h−1). But this speed is only accessible for the fastest extant terrestrial tetrapod, the cheetah (Acynonix jubatus). This unexpected result suggests that other explanations of the unusual tibial strength must be explored. The estimate based on allometry of the avian tibial diameter for a 70 kg terror bird yields a range from 1.8 to 2.2 cm (Cubo & Casinos 1998). The range does not include the direct measure obtained upon the width at the middle section of the tibial diaphysis giving a value of 3.2 cm (Alvarenga & Höfling 2003). This observation provides further evidence of excessive strength for the bones of Mesembriornis. It is clear that the maximum speed could be overestimated if the greatest forces that act on a limb are not for running. Indeed, the study of moas gives another suggestion. The moas were a group of giant terrestrial and hebivorous birds of the New Zealand islands. The leg bones of these birds are clearly overdesigned as already studied by other authors (Alexander 1983a, 1983b; Cracraft 1976). But, to gain some quantitative insight on the effect of excessive leg bones strength on maximum running speed we applied here the model to one specimen of moa. For Anomalopteryx, the model predicts a extraordinary speed of 31 m s−1∼112 km h−1. But the slowness of movement in these birds is well known from eighteenth century description upon the arrival of the Europeans (Alexander 1989). The main theoretical explanation for the model's overestimated prediction in this case came from considering the geographic isolation of its insular habitat and the lack of selective pressure generated by predators. Therefore, the metabolic cost of having high safety factors probably did not affect the fitness of the moas (Alexander 1989). But such a theoretical argument cannot be extended to Mesembriornis. The terror bird was a carnivore living in a large continent, thereby exposed to many ecological interactions with other fierce predators (Argot 2004).

According to some calculations about punches in martial arts (Walker 1975), a force of 3142 N is required to break a bone of 1 cm of radius and 20 cm in length. Refined calculations (Blum 1977) suggest that a force of 2355 N suddenly applied at the midpoint will suffice to fracture the same bone rigidly supported on its ends. The model applied here shows that the tibiotarsus of Mesembriornis was able to support a ground reaction force of 3.5 times the body weight, that means 2401 N. Therefore, this terror bird could have been able to fracture bones as long as those of a modern medium size ungulate like the saiga, Saiga tatarica, Thomson's gazelle, Gazella thomsoni or chamois, Rupicapra rupicapra (Blanco et al. 2003). This observation suggests the use of kicking for bone breaking as a possible food-processing behaviour, for terror birds, in order to access the bony marrow a dietary resource not frequently accessed by birds. But we mention, as an exception, the bearded vulture Gypaetus barbatus, which drops bones from high altitude against rocks, as a means of breaking them to access to the marrow (Campbell & Lack 1985). This behaviour could imply that Mesembriornis would occupy a special ecological niche.

Another possibility is that the strength of the bones of these species would be implied also in kicking to seize their prey. This vision would have an analogue in the African secretary bird, Sagittarius serpentarius (4 kg of body mass), which kills snakes with repeated kicks (Brehm 1880, Campbell & Lack 1985). The secretary bird belongs to the Sagittaridae family, with many osteological similarities with the phororhacids (Andrews 1899), but this example is not the best analogy since there are great differences in size. However, other larger terrestrial birds like ratites, with body masses of the same order as some terror birds, use their legs as weapons in interspecific and defensive fighting (Campbell & Lack 1985). Although our suggestions on kicking behaviour are highly speculative we can state, based on the mechanical model, that Mesembriornis was able to break a long bone of a medium size mammal without risk of breaking its own tibiotarsus. The use of legs as weapons is consistent with the morphology of the toes. The ungual phalanges of Mesembriornis, Patagornis and other species are large, curved and laterally compressed (Kraglievich 1932), a claw shape consistent with the function of stabbing prey, a well known behaviour in some modern birds (Campbell & Lack 1985). The exceptional bone strength of this bird is interesting on its own and could have relevant implications in further evolutionary and systematic studies of this group of birds.

All these palaeobiological suggestions could be useful in understanding the ecological role of terror birds and their interactions with large marsupial predators, such as the borhyaenids (Argot 2004). Also, it would be interesting, in future works, to consider, from a biomechanical point of view, the predatory interactions of terror birds, using their beaks and claws, against some groups of mammals such as the well armoured armadillos and glyptodonts (Alexander et al. 1999) in the Tertiary South American ecosystems.

Acknowledgments

We are grateful to R. Fariña, P. Arrighi, A. Rinderknecht, J. R. Hutchinson, P. Christiansen, G. Lecuona and N. Silvera.

References

  1. Alexander R.McN. Allometry of the leg bones of moas (Dinornithes) and other birds. J. Zool. 1983;200:215–231. [Google Scholar]
  2. Alexander R.McN. On massive legs of a moa (Pachyornis elephantopus, Dinornithes) and other birds. J. Zool. (Lond.) 1983b;201:363–376. [Google Scholar]
  3. Alexander R.McN. Columbia University Press; New York: 1989. Dynamics of dinosaurs & others extinct giants. [Google Scholar]
  4. Alexander R.McN. Princeton University Press; 2003. Principles of animal locomotion. [Google Scholar]
  5. Alexander R.McN, Maloiy G.M.O, Njau R, Jayes A.S. Mechanics of running of the ostrich (Struthio camelus) J. Zool. 1979;187:169–178. [Google Scholar]
  6. Alexander R.McN, Fariña R, Vizcaíno S.F. Tail blow energy and carapace fractures in a large glyptodont (Mammalia, Xenarthra) Zool. J. Linn. Soc. 1999;126:41–46. [Google Scholar]
  7. Alvarenga H.M.F, Höfling E. Systematic revision of the Phorusrhacidae (Aves: Ralliformes) Papéis Avulsos de Zoologia. Museu de Zoologia da Universidade de Sao Paulo. 2003;43:55–91. [Google Scholar]
  8. Andrews C. On the extinct birds of Patagonia. Trans. Zool. Soc. Lond. 1899;15:55–86. [Google Scholar]
  9. Argot C. Evolution of South American mammalian predators (Borhyaenoidae): anatomical and palaeobiological implications. Zool. J. Linn. Soc. 2004;140:487–521. [Google Scholar]
  10. Baskin J.A. The giant flightless bird Titanis walleri (Aves: Phorusrhacidae) from the Pleistocene coastal plain of South Texas. J. Vert. Paleontol. 1995;15:842–844. [Google Scholar]
  11. Biewener A.A. Scaling body support in mammals: limb posture and muscle mechanics. Science. 1989;245:45–48. doi: 10.1126/science.2740914. [DOI] [PubMed] [Google Scholar]
  12. Biewener A.A. Biomechanics of mammalian terrestrial locomotion. Science. 1990;250:1097–1103. doi: 10.1126/science.2251499. [DOI] [PubMed] [Google Scholar]
  13. Blanco R.E, Mazzetta G.V. A new approach to evaluate the cursorial ability of the giant theropod Giganotosaurus carolinii. Acta Palaeontol. Pol. 2001;46:193–202. [Google Scholar]
  14. Blanco R.E, Gambini R, Fariña R.A. Mechanical model for theoretical determination of maximum running speed in mammals. J. Theor. Biol. 2003;222:117–125. doi: 10.1016/s0022-5193(03)00019-5. [DOI] [PubMed] [Google Scholar]
  15. Blum H. Physics and the art of kicking and punching. Am. J. Phys. 1977;45:61–64. [Google Scholar]
  16. Brehm A.E. Wien Bibliographisches Institut; Leipzig: 1880. Brehms Tierleben. Allgemeine Kunde des Tierreichs. [Google Scholar]
  17. Campbell B, Lack E. Buteo Books; Vermillion: 1985. A dictionary of birds. [Google Scholar]
  18. Christiansen P. Strenght indicator values of theropod long bones, with comments on limb proportions and cursorial potential. Gaia. 1998;15:241–255. [Google Scholar]
  19. Christiansen P. Locomotion in terrestrial mammal: the influence of the body mass, limb length and bone proportions on speed. Zool. J. Linn. Soc. 2002;136:685–714. [Google Scholar]
  20. Cracraft J. The hindlimb elements of the moas (Aves: Dinornithidae): a multivariate assessment of size and shape. J. Morphol. 1976;150:495–526. [Google Scholar]
  21. Cubo J, Casinos A. The variation of the cross sectional shape in the long bones of birds and mammals. Ann. Sci. Nat. 1998;1:51–62. [Google Scholar]
  22. Farley C.T. Maximum speed and mechanical power output in lizards. J. Exp. Biol. 1997;200:2189–2195. doi: 10.1242/jeb.200.16.2189. [DOI] [PubMed] [Google Scholar]
  23. Farlow J.O, Smith M.B, Robinson J.M. Body mass, bone “strength indicator”, and cursorial potential of tyrannosaurus rex. J. Vert. Paleontol. 1995;15:713–725. [Google Scholar]
  24. Garland T, Jr, Janis C.M. Does metatarsal/tarsal ratio predict maximal running speed in cursorial mammals? J. Zool. 1993;229:133–151. [Google Scholar]
  25. Hutchinson J.R. Biomechanical modeling and sensitivity analysis of bipedal running ability. I. Extant taxa. J. Morphol. 2004;262:421–440. doi: 10.1002/jmor.10241. [DOI] [PubMed] [Google Scholar]
  26. Hutchinson J.R, García M. Tyrannosaurus was not a fast runner. Nature. 2002;415:1018–1021. doi: 10.1038/4151018a. [DOI] [PubMed] [Google Scholar]
  27. Irschik D.J, Garland T., Jr Integrating function and ecology in studies of adaptation: investigations of locomotor capacity as a model system. Annu. Rev. Ecol. Syst. 2001;32:367–396. [Google Scholar]
  28. Kraglievich L. Una gigantesca ave fósil del Uruguay. Devincenzia gallinali n. gen. n. sp., tipo de una nueva familia, Devincenziidae, del Orden Stereornithes. Ann. Mus. Hist. Nat. Mont. 1932;3:323–355. [Google Scholar]
  29. Marshal L.G, Cifelli R.L. Analysis of changing diversity patterns in Cenozoic land mammals age faunas, South America. Palaeovertebrata. 1990;19:169–210. [Google Scholar]
  30. Moreno F.P. Breve reseña de los progresos del Museo La Plata, durante el segundo semestre de 1888. Boletin del Museo La Plata. 1889;3:1–44. [Google Scholar]
  31. Moreno F.P, Mercerat A. Catálogo de los pájaros fósiles de la República Argentina conservados en el Museo de La Plata. Anales del Museo de La Plata. 1891;1:7–71. [Google Scholar]
  32. Patak A.E, Baldwin J. Pelvic limb musculature in emu Dromaius novaehollandiae (Aves: Struthioniformes: Dromaiidae): adaptations to high-speed running. J. Morphol. 1998;238:23–37. doi: 10.1002/(SICI)1097-4687(199810)238:1<23::AID-JMOR2>3.0.CO;2-O. [DOI] [PubMed] [Google Scholar]
  33. Paul G.S. Limb design, function and running performance in ostrich-mimics and tyrannosaurs. Gaia. 1998;15:257–270. [Google Scholar]
  34. Rinderknecht A, Noriega J.I. Un nuevo género de Anhingidae (Aves: Pelecaniformes) del Plioceno–Pleistoceno del Uruguay (Formación San José) Ameghiniana. 2002;39:183–191. [Google Scholar]
  35. Tambussi C, Ubilla M, Perea D. The youngest large carnassial bird (Phorusrhacidae, Phorusrhacinae) from South America (Pliocene—Early Pleistocene of Uruguay) J. Vert. Paleontol. 1999;19:404–406. [Google Scholar]
  36. Walker J.D. Karate strikes. Am. J. Phys. 1975;43:845–849. [Google Scholar]
  37. Webb S.D. Ecogeography and the Great American interchange. Paleobiology. 1991;17:266–280. [Google Scholar]
  38. Weyand P.G, Sternlight D.B, Bellizzi M.J, Wright S. Faster top running speeds are achieved with greater ground forces not more rapid leg movements. J. Appl. Physiol. 2000;89:1991–1999. doi: 10.1152/jappl.2000.89.5.1991. [DOI] [PubMed] [Google Scholar]
  39. Zeffer A, Johansson L.C, Marmebro Å. Functional correlation between habitat use and leg morphology in birds (Aves) Biol. J. Linn. Soc. 2003;79:461–484. [Google Scholar]

Articles from Proceedings of the Royal Society B: Biological Sciences are provided here courtesy of The Royal Society

RESOURCES