The effect of disease life history on the evolutionary emergence of novel pathogens

Abstract

We present a general analytical result for the probability that a newly introduced pathogen will evolve adaptations that allow it to maintain itself within any novel host population, as a function of disease life-history parameters. We demonstrate that this probability of ‘evolutionary emergence’ depends on two key properties of the disease life history: (i) the basic reproduction number and (ii) the expected duration of an infection. These parameters encapsulate all of the relevant information and can be combined in a very simple expression, with estimates for the rates of adaptive mutation, to predict the probability of emergence for any novel pathogen. In general, diseases that initially have a large reproductive number and/or that cause relatively long infections are the most prone to evolutionary adaptation.

1. Introduction

The majority of existing human infectious diseases have originated from other animals, from the beginning of domestication up until the present time (Diamond 1997; Woolhouse 2002; e.g. influenza, plague, tuberculosis, malaria, HIV, Ebola fever, SARS). In some instances, ecological changes are sufficient to yield the entry and maintenance of a novel pathogen in the human population (sedentary lifestyles, animal domestication, urbanization; Schrag & Wiener 1995). In other instances, however, the zoonotic pathogen causes only sporadic cases upon each introduction but is unable to sustain itself in humans without repeated introductions. The most familiar examples involve the various strains of avian influenza that have caused small clusters of infections in humans (Webster et al. 1992; Earn et al. 2002). Such pathogens nevertheless remain a serious public health threat because, at some point, they might acquire specific adaptations that allow them to spread from human to human more effectively. For instance, SARS coronavirus has most likely been unsuccessfully introduced several times in humans, before provoking a significant epidemic (Peiris et al. 2004). The eventual epidemic then became possible, presumably because of the adaptation of viruses to humans (The Chinese SARS Molecular Epidemiology Consortium 2004).

Our aim here is to provide a very general analysis of the risk of pathogen adaptation and emergence as a function of differences in disease life histories. By disease life history we mean the temporal pattern of transmission, mortality and/or recovery that occurs during an infection (Day 2003). For example, suppose there are two different novel pathogens that might accidentally be introduced into the human population. One of these is not transmitted in the beginning of infection but only after a certain amount of time (e.g. SARS viruses are weakly transmitted in the first five days of infection), whereas the other has its transmission spread more evenly all along the infection, but provokes shorter infections. Which of these pathogens is more prone to evolving adaptations that will allow it to persist in the human population? It is this type of question that our analysis will answer, in terms of very general disease life-history parameters.

Consider a pathogen, newly introduced into humans, but unable to sustain itself. This pathogen might generate some new infections in humans, causing a cluster of cases of some size, but it will eventually die out owing to its poor overall transmissibility from human to human. One can describe the life history of an infection caused by this pathogen using various parameters, including its transmission rate, pathogen-induced mortality rate and clearance rate during each stage of infection, as well as its expected duration and/or the total number of new infections generated. It is not immediately obvious which of these pieces of information will be most important for determining the risk of pathogen adaptation, or whether a combination of them is required.

The most widely quantified single descriptor of disease life histories is the reproductive number, R₀, which is essentially the number of new infections that are generated over the course of a single infection (Anderson & May 1991). By definition, if the pathogen is originally unable to persist in humans, then its reproductive number is less than one. An interesting recent paper by Antia et al. (2003) demonstrates that this reproductive number also contains important information about the risk of pathogen adaptation as well. In particular, they show that novel pathogens with reproductive numbers closer to one (in the human population) pose a greater risk of adaptation because they can remain within the population for substantially longer periods of time after each occasional entrance, and this will, therefore, increase the probability that adaptation occurs before extinction.

The results of Antia et al. (2003) should prove to be extremely useful for identifying potentially threatening pathogens, but they also lead one to ask if there might be other important attributes of disease life histories that affect the likelihood of adaptation. In the models developed below we demonstrate that there are, in fact, other crucial disease life-history parameters. This is done by first examining two relatively simple but specific models. From there we then derive some very general results that encompass arbitrary pathogen life histories, and we show that the crucial disease life-history attributes affecting the likelihood of adaptation can be summarized with two intuitive quantities: (i) the reproductive number of the disease and (ii) the expected duration of an infection. Diseases with large reproductive numbers and/or long infections are the most prone to adaptation in novel hosts and both of these factors can have substantial effects. In terms of their relative effects, our results also suggest that the expected duration of an infection is often likely to be a more important determinant of the probability of evolutionary emergence than is the reproductive number of the disease. In these circumstances, introduced diseases that cause few but long infections in humans are more apt to evolve adaptation than those that cause many short infections.

2. Models and analyses

Our aim is to calculate the probability that an introduced pathogen, originally maladapted to humans, generates adaptive mutation(s) before extinction, and therefore eventually invades the host population (see also Antia et al. 2003; Iwasa et al. 2004). In contrast with Antia et al. (2003) who consider discrete generations, we model the life cycle of infections in continuous-time, and begin with two simple models.

(a) One-stage disease life history

Suppose that infections by the introduced pathogen can be characterized by a single stage such that they generate secondary infections (by transmission to susceptible hosts) at a constant rate b over the entire duration of infection. An infection might also end at any time owing to host death or clearance by the immune system, and we suppose that these combined events happen at an overall fixed per capita rate of d throughout the entire infection. The expected length of an infection by the introduced strain is, therefore, L=1/d, and the pathogen's reproductive number (i.e. the expected number of new infections caused by a single infected individual) is R₀=b/d. Immediately following an introduction, the pathogen is assumed to be maladapted to humans and thus its rate of production of new infections is lower than the rate at which infections end (i.e. b<d). As a result, in the absence of evolution, extinction will eventually occur (figure 1a,b). Furthermore, we assume that the total outbreak size, in the absence of evolution, is small enough that it does not cause an appreciable decline in the number of susceptible individuals.

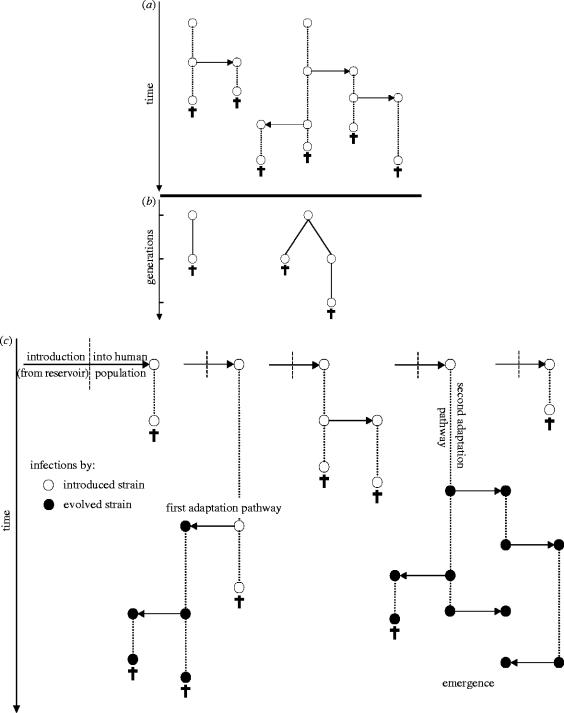
Figure 1.

Schematic of the transmission chain and emergence of an infectious disease. Introductions from the reservoir are followed by survival, transmission and death in the human population. In (a) and (c) the course of infections is symbolized by dotted lines; infections can reproduce at any time by transmission to susceptible hosts (right or left arrows), or die owing to immune clearance or host mortality (crosses). The introduced strain (open circles) is unable to spread because its reproduction rate, b, is lower than its death rate, d. (b) is a generation-based equivalent of (a), constructed in the same manner as fig. 1 of Antia et al. (2003). This is constructed by following the introduced infection of (a), and counting the total number of secondary infections that it generates (R₀ in expectation). These are then noted as offspring in the next generation and the procedure is repeated for each infection that is generated. The total number of reproduction events in the chain of transmission of the introduced pathogen, B, can be obtained graphically from (a), by considering one introduction event and counting the overall number of horizontal links in the arborescence generated. It can also be obtained from (b) by counting the number of links between two infections. The cumulative length of introduced infections, T, can be also obtained graphically from (a) by considering one introduction event and counting the overall length of vertical links in the transmission chain. T cannot be measured from (b) (nor from fig. 1 of Antia et al. 2003), because it lacks information relative to time. In (c) adaptation can occur; a single mutation (affecting b and/or d) is able to bring the pathogen above the epidemic threshold (b_a>d_a). The adaptive mutation can occur along two pathways: first, at each transmission event, the new infection can carry the mutation with a probability u (first adaptation pathway); second, the mutation can reach fixation during the course of an infection, at a rate μ per unit of time (second adaptation pathway). The infections caused by the evolved strain (filled circles) can go on to cause an epidemic (emergence).

During the period of time in which the introduced pathogen remains extant within the human population, adaptive mutations will occasionally appear (figure 1c), and we need to specify the mechanism by which this takes place. Mutations are generated at low frequency within infections, owing to errors in the replication of the pathogen. But the benefit of an adaptive mutation is to improve the infections' R₀, and hence it can be expressed only if that mutation reaches a large frequency within an infection. This within-host fixation might occur through two distinct mechanisms (figure 1c). First, the adaptive mutation might fix by chance within a secondary infection owing to a transmission bottleneck. Second, the mutation might be favoured in local competition between individual pathogens within a host, and hence directly reach a large frequency within the infection where it first appeared. Indeed, for pathogens that are recently introduced into a new host, it is likely that at least a fraction of beneficial mutations that might occur will represent basic adaptations (e.g. better resistance to immunity, improved affinity for host tissues), and therefore will be beneficial both to microbes in local competition within a host and to the entire infection.

Mathematically, we model these mechanisms with two distinct parameters. First, at each transmission event, the secondary infection has an overall probability, u, of being fixed for an adaptive mutation (i.e. the first pathway in figure 1c). Second, each infection can change in genotype at any time owing to the fixation of an adaptive mutation through within-host mechanisms. We assume that this occurs at an overall rate μ (i.e. the second pathway in figure 1c). If only a single adaptive mutation is required to allow the pathogen to persist within the human population, then the probability of evolutionary emergence from an initially maladapted pathogen is approximately (Appendix A)

$$P\approx \frac{1}{1-R_0}[u{R}_0+\mu L]P_{\text{a}},$$ 2.1

where (1/(1−R₀))[uR₀+μL] is the probability that an appropriate adaptation occurs, and P_a is the probability of an epidemic, given that the adaptation has occurred, which is equal to P_a=1−1/R*, where R* is the reproductive number of the adapted pathogen (which is greater than one by definition). Note that equation (2.1) is derived from the exact expression of the probability of emergence (equation (A 3)), as a first-order approximation, assuming small mutation rates. Also recall that R₀=b/d is the reproductive number of the maladapted pathogen and L=1/d is the expected duration of infections that it causes.

In the case where m adaptive mutations are needed for adaptation to humans, and assuming that all not-yet-adapted strains have the same life-history traits, b and d, the probability of emergence of the pathogen can be derived by recurrence as (see Appendix A)

$$P\approx \frac{1}{{(1-R_0)}^m}{[u{R}_0+\mu L]}^m{P}_{\text{a}},$$ 2.2

where all higher order terms of mutation rates have been dropped. Note that all the effects of mutation rates of order lower than m are nil, because at least m mutation events must occur for emergence to take place. As a result, equation (2.2) is an m^th order approximation.

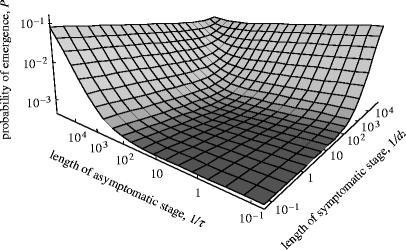
Figure 2 plots the exact expression of the probability of emergence (equation (A 3)), as a function of the reproductive number and the expected duration of an infection. From equations (2.1) and (2.2), we can see that both parameters affect the probability of emergence positively, and figure 2 illustrates that either of them alone can have a substantial effect. The introduced pathogen is more likely to generate adaptations when its infections are long-lived and/or well transmitted.

Figure 2.

Probability of emergence in the single-stage model, plotted as a function of the reproductive number (R₀=b/d) and expected length (L=1/d) of introduced infections (equation (A 3)). The probability for a secondary infection to carry an adaptive mutation (first adaptation pathway) is u=10⁻³; the rate of adaptation in the course of infection (second pathway) is μ=10⁻⁶; the probability of emergence of adapted strains is P_a=0.5 We could also estimate the probability of emergence of pathogens from Monte Carlo simulations, which confirmed the validity of our analytical model (not shown).

In order to understand the role of each adaptation pathway in more detail, we can directly interpret the simple mathematical expression given in equation (2.1). The two terms in brackets measure the contribution of each type of mutation process to emergence. The first term is the contribution of adaptive mutations occurring at transmission (happening with probability, u). Bringing the denominator inside the parenthesis, we can see that the magnitude of this effect is proportional to the ratio B=R₀/(1−R₀). This quantity is simply the expected number of transmission events that occur prior to extinction. In particular, this can be directly calculated as $\sum _{i=1}^{+\infty }{(R_0)}^i$, which simplifies to R₀/(1−R₀)=B (see also figure 1a,b for a graphical interpretation of B). In a situation where adaptations occur at the moment of transmission, the risk of emergence depends on the total number of transmission events in the life of the introduced strain.

The second term in the brackets of equation (2.3) measures the contribution of adaptations occurring as a result of within-host selection during the course of an infection. The effect of the mutation rate along this pathway (μ) is proportional to the ratio T=L/(1−R₀) or equivalently T=1/(d−b). This quantity is simply the sum of the expected durations of all the infections generated by the introduced pathogen. In particular, it can be directly calculated as $(1/d)\sum _{i=0}^{+\infty }{(R_0)}^i$, which simplifies to (1/d)[1/(1−R₀)]=1/(d−b)=T (see also figure 1a for the graphical interpretation of T). In a situation where adaptations can occur at any time during the course of each infection, the risk of emergence depends on the cumulative duration of all infections.

(b) Two-stage life history

The above results apply to a very simple disease life history but how are they altered for more realistic situations? We next go one step further in this direction and suppose that the infection starts with an asymptomatic stage, during which the pathogen is not transmitted (b₁=0) and the host has a low mortality (d₁ is low). The pathogen is transmitted and impacts the host mortality only during the second stage of infection (which is characterized by the rates, b₂ and d₂). Infections progress from the first to the second stage at a given ‘transition’ rate τ. We assume that the mutation rates along both pathways (u and μ) are the same in the two stages. We then use the same method as above to derive a first-order approximation for the probability of emergence of the pathogen, valid for low mutation rates. It is again given by equation (2.1) but with

$$R_0=\frac{\tau }{d_1+\tau }\frac{b_2}{d_2}\text{and}L=\frac{1}{\tau +b_1}+\frac{\tau }{\tau +b_1}\frac{1}{d_2}.$$ 2.3

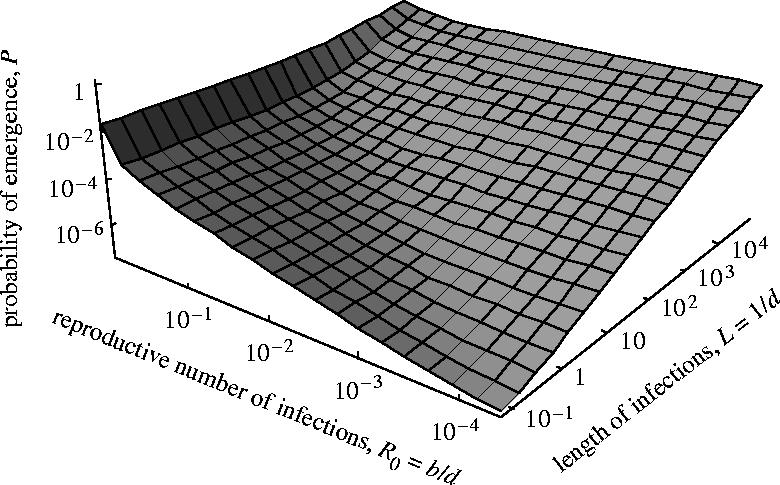
In this more complex disease life history, we again see that the probability of emergence of the pathogen can be expressed with two components measuring the contribution of each adaptation pathway (equations (2.1) and (2.3)). And again R₀ is the reproductive number and L is the expected duration of an infection (which are now given by the more complex expressions in equation (2.3)). As a result, again the two mutation processes contribute to the probability of emergence in a way that depends on the total number of transmission events prior to extinction and the cumulative duration of all infections prior to extinction respectively. Therefore, in this case as well, the overall consequences of these findings are that (i) introduced pathogens are more dangerous when R₀ is high, but (ii) for a given R₀, pathogens that provoke durable infections (large L) are intrinsically more dangerous. Figure 3 plots the exact expression of the probability of emergence, as a function of the length of the symptomatic and asymptomatic stages, keeping the overall pathogen reproductive number constant. For a given reproductive number, the introduced disease is more likely to emerge if it provokes durable infections.

Figure 3.

Probability of emergence in the two-stage model, plotted as a function of the expected length of the first and second stage (1/τ and 1/d₂, respectively), the overall pathogen fitness (R₀=b₂/d₂) being kept constant. The pathogen is transmitted and impacts host mortality only during the second stage (b₁=0 and d₁=0). All other parameters are as in figure 2.

(c) General life histories

The correspondence between the results for two simple disease life histories suggest that similar results might hold for more complex life histories. Indeed, Appendix B demonstrates that these results are extremely general. Regardless of the pattern of transmission, death, and clearance during an infection, equation (2.1) continues to be valid. In other words, the transmission rate, death rate and clearance rate might change with infection age for each infected individual, but it is still the disease reproductive number and the expected duration of an infection that govern the probability of evolutionary emergence.

In fact, these results generalize even further to situations in which the rate of within-host adaptation, μ, changes with infection age. This is probably often the case as a result of changes in the within-host density and/or replication rate of pathogens. For example, we might expect that the rate at which strains arise via within-host selection that have R>1 (i.e. μ) increases with infection age, owing to the accumulation of incremental adaptations over time within a host. In this case, a slightly more general form of equation (2.1) holds (Appendix B)

$$P=\frac{1}{1-R_0}(\overline{\mu }(L)L+u{R}_0).$$ 2.4

Here, $\overline{\mu }(L)=\frac{1}{L}{\int }_0^L\mu (s)\text{d}s,$ is the average rate of within-host adaptation for an infection of length L, and it will be a strictly increasing function of L whenever μ(s) increases with infection age. This thereby imparts an additional risk of having long infections; they have a higher average rate of within-host adaptation.

Interestingly, in this more general context, it is no longer solely the total cumulative duration of all infections that determines the risk of within-host adaptation. Recall that, when the rate of within-host adaptation, μ, is constant during an infection, having many very short infections yields an equivalent risk of within-host adaptation as having few long infections (since the total cumulative duration of all infections is the same in both cases). When μ(s) increases with infection age, however, having many short-lived infections yields a lower probability of within-host adaptation than having a few long-lived infections, because the latter suffer high average rates of evolutionary adaptation (Appendix B).

In any case, the risk of adaptation posed by novel pathogens can, quite generally, be characterized by two simple indices of their life histories. Those diseases with large reproduction numbers and/or long infections pose the greatest threat of adaptation. Moreover, the significance of each of these parameters depends on the extent to which adaptation is likely to occur through mutations arising at transmission versus arising as a result of within-host competition during an infection. Both of these routes are undoubtedly very important for pathogens that have recently begun to exploit a new host.

3. Discussion

When a novel pathogen is first introduced into the human population it will be able to sustain itself only if its reproductive number is larger than one (i.e. R₀>1). In this case, the pathogen is said to be above the epidemic threshold, and this is clearly the worst situation from the perspective of human health. Even if the pathogen's reproductive number is lower than one, however, the pathogen might nevertheless eventually evolve to sustain itself in the human population through the generation of adaptive mutations. The aim of this paper is to provide a very general analysis of the risk of pathogen adaptation and emergence, as a function of disease life-history parameters.

Our results demonstrate that the risk of pathogen adaptation is largely determined by two simple disease life-history parameters: (i) the basic reproduction number and (ii) the expected duration of an infection. The first of these parameters is exactly that identified by Antia et al. (2003) as being an important determinant of disease emergence, but the second represents an additional aspect of disease life history that can have an equally, if not more significant, effect on the probability of pathogen adaptation. We discuss each of these in turn.

The effect of the reproductive number on the probability of emergence arises from mutations that reach fixation within a host as a result of a bottleneck during the moment of transmission from one host to another. In general, pathogens are less likely to adapt, and thus emerge, if they initially have a reproductive number that is far below the epidemic threshold (R₀≪1). From an epidemiological standpoint this occurs because the reproductive number of the pathogen (R₀) determines the expected number of times that it is transmitted from one host to another prior to going extinct. Each transmission event represents an opportunity for an adaptive mutation to reach fixation, and hence adaptation is more likely when R₀ is close to one.

The occurrence of mutations at the moment of transmission is analogous to mutations occurring during the reproduction of non-microbial invaders (e.g. invasive plant species), where adaptive mutations actually occur at the moment of reproduction. In the case of pathogens, however, the situation is more subtle. Adaptive mutations are initially generated randomly among individual microbes within infections, which would be equivalent to the generation of mutations among gametes in an invasive animal or plant. These random modifications can then reach fixation within a host during transmission bottlenecks as discussed above, but they can also reach fixation by rising in frequency directly within the host body over the course of an infection itself. This alternate pathway, called within-host adaptation, strongly affects the likelihood of adaptation and emergence of an introduced pathogen. In particular, for a given reproductive number, R₀, the risk of emergence is larger for pathogens that provoke long-lasting infections (figure 2). Long infections are intrinsically more prone to adaptive evolution because the amount of time during which within-host selection can operate is increased.

If the rate of occurrence of within-host adaptation increases during the course of an infection (e.g. through an increased rate of generation of appropriate mutations) then long-lived infections exhibit an additional increase in the likelihood of adaptive evolution, over and above the simple effect due to the increased time available for adaptation. In this case, long-lived infections also experience a greater average rate of within-host adaptation (see equation (2.4)). As a result, from the standpoint of within-host evolution alone, having few long-lived infections is more dangerous in terms of evolutionary emergence than having many short-lived infections.

The risk of emergence of a given introduced pathogen is thus strongly affected by the actual mechanism of adaptation available in this species, the key point being whether adaptation can take place directly within each host or not. We suggest that within-host adaptation might be very significant in numerous cases, and that it might often be even more important than transmission-dependent mutations.

As an example, consider the adaptation of pathogens that are being driven to extinction by antibiotics. The above results can be readily applied to this situation. Antibiotic resistance is probably most likely to occur by mutation (or recombination with other bacterial species) and then fixation within an infection owing to local selection imposed by the antibiotic. Indeed it is probably unreasonable to think that antibiotic resistance reaches fixation only by chance at the time of transmission to a new host. The same reasoning applies to the evolution of escape mutants in the presence of vaccine use as well. As a consequence, the key parameters that treatments should control are not only the reproductive number of an infection but its duration as well. In other words, antibiotics and other medical interventions should be used in a way that rapidly clears infections rather than simply reduces their transmissibility.

In the context of novel pathogens, when a pathogen is first introduced into a new host species, a large fraction of the initial beneficial mutations will likely represent basic adaptations to this new host, such as better resistance to immunity or improved affinity for host tissues (see Webby et al. 2004). In other words, pathogen adaptation is likely to be characterized by an increase of its replication ability within the host body. For instance, in the case of influenza, viruses that are adapted to birds have been shown to replicate poorly in humans, and vice versa (Webby et al. 2004). Therefore, in addition to being favourable to the infection as a whole, a large fraction of the initial adaptations occurring in a novel pathogen are probably beneficial to microbes in local competition within a host as well. Moreover, the large population size and short generation time of microbes within a host should also enhance the importance of this process since within-host populations can then ‘test’ numerous mutations. This contrasts with the adaptive mutations that are not favoured locally and that can fix only by chance at transmission. Mutations fixing at transmission are a somewhat random subset of all the mutations that have occurred, and many of these are likely to be deleterious or neutral to the infection.

Further, processes other than those explicitly modelled here can also take place during the course of infections and can influence the probability of emergence. For instance, if transmission bottlenecks are important, then newly established infections carry very few neutral polymorphisms. In this case, neutral polymorphism increases during the course of an infection owing to de novo mutations. As a result, even in the absence of within-host adaptation per se, the probability of adaptation at transmission, u, is expected to be an increasing function of the length of infection, again suggesting that long-lasting infections should be more dangerous. Second, mutation is not the only source of adaptation, but rather recombination and/or reassortment between pathogen strains within a host can also occur. For instance in the case of influenza, reassortment between an avian strain and a human strain is thought to be the decisive event leading to the emergence of influenza pandemics, and this event is all the more likely to occur for avian influenza strains that provoke long infections in each human that they accidentally infect.

We close by making a few remarks about the simplifying assumptions that have been used in the analysis. First we assumed that each infection is established by a single pathogen genotype. Therefore, any new infection that is generated is either a wild-type infection (with a probability 1−u) or a mutant infection (with a probability u), and cannot be made up of an intermediate frequency of both types (see also Antia et al. 2003). Second, and more importantly for the present paper, we considerably simplified the process of within-host adaptation. We assumed that the predominant genotype of an infection could change instantaneously (at a rate μ(s) where s is infection age) into a mutant infection owing to ‘within-host adaptation’. In other words, once an adaptive mutation has appeared within an infection, its reaches fixation effectively instantaneously. This assumption is very useful for simplifying the mathematical analysis; however, it has the dangerous side effect of providing a somewhat caricatured image of within-host adaptation. It is very likely that within-host selection is not strong enough in many instances to yield the complete fixation of adaptive mutants within the course of a single infection. Instead, within-host selection might only yield an increase in the frequency of adaptive mutants during each infection. Even in this case, however, within-host selection (and all other within-host processes) will boost the probability of emergence in long-lasting infections by increasing the probability of an adaptive mutation being transmitted to susceptible hosts. Thus the qualitative conclusions reached here should nevertheless be quite robust.

Appendix A

Appendix A. Branching process and probability of emergence

Consider an infection caused by a novel pathogen that is initially unable to spread in the human population (i.e. its birth rate is lower than its death rate, b<d). Suppose that a single mutation is sufficient for adaptation such that b_a>d_a, where the subscript a refers to the adapted pathogen. In order to calculate the probability of emergence, we first derive the probability, Q(t), that an introduced pathogen, present in the population at time t, ultimately goes extinct. Let us also define Q_a(t) as the probability that an adapted pathogen, present in the population at time t, ultimately goes extinct. Equations for Q(t) and Q_a(t) can be derived by considering all the events that might occur during an infinitesimal period dt

$$\begin{array}{l}\begin{array}{l}Q(t)=b(1-u)\text{d}t{(Q(t+\text{d}t))}^2+bu\text{d}tQ(t+\text{d}t)Q_{\text{a}}(t+\text{d}t)\\ +\mu \text{d}t{Q}_{\text{a}}(t+\text{d}t)+d\text{d}t+Q(t+\text{d}t)\\ [1-b\text{d}t-d\text{d}t-\mu \text{d}t],\end{array}\hfill \\ \begin{array}{l}{Q}_{\text{a}}(t)=b_{\text{a}}\text{d}t{(Q_{\text{a}}(t+\text{d}t))}^2+d_{\text{a}}\text{d}t\\ +Q_{\text{a}}(t+\text{d}t)[1-b_{\text{a}}\text{d}t-d_{\text{a}}\text{d}t].\end{array}\hfill \end{array}\}$$ A1

First, the maladapted strain might give rise to a new infection (with probability bdt) in which case this infection will also be maladapted with probability (1−u) and it will have mutated to the adapted strain with probability u. In these cases, the probability of ultimate extinction is Q(t+dt)² and Q(t+dt)Q_a(t+dt), respectively. Second, the infection can give rise to an adaptive mutation as a result of within-host processes with probability μdt, in which case extinction occurs with probability Q_a(t+dt). Finally, the infection itself ends and extinction occurs with probability ddt. Similar considerations hold for the equation for Q_a(t).

Equation (A 1) assumes that the introduced strain never attains high prevalence and, therefore, does not affect the density of susceptible hosts. In contrast, the evolved strain is assumed to be very efficient (b_a≫d_a). Therefore, its fate is decided while it is still at very low frequency. As a result, the density of susceptible hosts can be assumed constant (n) during the whole stochastic process, and the rates at which both genotypes produce new infections (b=βn and b_a=β_an) are therefore also constant. Accordingly, the probabilities of ultimate loss (Q and Q_a) can be derived by modeling the demography of the strains as a branching process (Fisher 1922, 1930 pp. 73–83; Haldane 1927; Antia et al. 2003), i.e. a single copy of each strain, present at time t, has the same probability of being lost as a copy present at t+dt. Therefore, Q and Q_a are independent of time and equation (A 1) yield

$$\begin{array}{l}b(1-u){(Q)}^2+buQ{Q}_{\text{a}}+\mu Q_{\text{a}}+d-Q(b+d+\mu )=0,\hfill \\ b_{\text{a}}{(Q_{\text{a}})}^2+d_{\text{a}}-Q_{\text{a}}(b_{\text{a}}+d_{\text{a}})=0.\hfill \end{array}\}$$ A2

The second equation in (A 2) can be solved to give Q_a=d_a/b_a, and this can then be used to calculate Q, and correspondingly the probability of emergence P=1−Q, as

$$P=(({(b+d+\mu -bu{Q}_{\text{a}})}^2-4b(1-u)(d+\mu Q_{\text{a}}){)}^{1/2}-d-\mu +b(1-u(2-Q_a)))/(2b(1-u)).$$ A3

Finally, developing P in a Taylor series to the first-order in the mutation parameters (u and μ) yields equation (2.1) in the text.

In the case where m adaptive mutations are required for adaptation, the equivalent of equation (A 1) can be written as a system of m equations

$$\begin{array}{l}\begin{array}{l}{b}_i(1-u){(Q_i)}^2+b_{i}u{Q}_i{Q}_{i+1}+\mu Q_{i+1}\\ +d_i-Q_i(b_i+d_i+\mu )=0,\forall i\in [0,m-1],\end{array}\hfill \\ b_m{(Q_m)}^2+d_m-Q_m(b_m+d_m)=0,\hfill \end{array}\}$$ A4

where the subscript i indicates the number of adaptive mutations carried by the genotype and Q_i is the probability that a given pathogen is ultimately lost, conditional on the fact that this pathogen carries i adaptive mutations. This system can be solved step-by-step, from Q_m=d_m/b_m to Q_m−1, … ,Q_m−j… down to Q₀=Q and finally to P=1−Q. In the analysis presented here, we assume a simple scenario, the jackpot model (Antia et al. 2003), where the life-history traits (b_i and d_i) of the pathogens with intermediate number of mutations (i<m) are identical to that of the initial pathogen (equal to b and d). The properties of the adapted strain are b_m=b_a and d_m=d_a.

One can then use a recurrence reasoning. The probability that an introduced pathogen generates one adaptive mutation and ultimately emerges is the probability of emergence P as given by equation (A 3), except that Q_a must be replaced by Q₁ the probability of ultimate loss for a pathogen carrying one adaptive mutation. Assuming that the opposite probability P₁=1−Q₁ is low (which is reasonable as more than one adaptive mutation is required to spread), the probability of emergence can be expressed by a Taylor development to the first-order on P₁ and on mutation parameters as P=[Bu+Tμ+o(u)+o(μ)]P₁+o(P₁), where T=L/(1−R₀) and B=R₀/(1−R₀). The probability of emergence of the strain with one mutation can in turn be expressed as P₁=[Bu+Tμ+o(u)+o(μ)]P₂+o(P₂), assuming that P₂ is low. Therefore, the probability of emergence gives approximately P≈[Bu+Tμ]²P₂. This can be repeated m times to yield the probability of emergence P≈[Bu+Tμ]^mP_a, which is equation (2.2) of the text. This derivation assumes that the probability of emergence of all non-adapted strains (P_i,∀i<m) are low but it does not make any assumption about the probability of emergence of the adapted strain (P_a=P_m).

Appendix B

Appendix B. Probability of emergence in the general case

To derive general results for pathogens with arbitrary life histories we need to take a different approach. Suppose that a novel pathogen is introduced into the human population. We would like to calculate the probability that at least one adaptive mutation occurs prior to the pathogen lineage going extinct. First let's condition on the total number of transmission events, τ, that occur before the pathogen dies out, as well as the realized durations of all of the τ+1 infections (denoted by L₁,L₂, …,  L_τ+1). For maximum generality, we allow the rate at which adaptation occurs via with-host processes (i.e. μ) to change with infection age. For example, we might sometimes expect that the rate at which adaptation occurs during an infection is higher later in an infection. In this case, the probability that at least one adaptive mutation occurs during the entire outbreak is one minus the probability that no mutations occur: $1-{(1-u)}^{\tau }{e}^{-\underset{0}{\overset{L_1}{\int }}\mu (s)\text{d}s}{e}^{-\underset{0}{\overset{L_2}{\int }}\mu (s)\text{d}s}\dots e^{-\underset{0}{\overset{L_{\tau +1}}{\int }}\mu (s)\text{d}s}$. This can be written as $1-{(1-u)}^{\tau }\text{exp}(-\overline{\mu }(L_1)L_1-\overline{\mu }(L_2)L_2\cdots -\overline{\mu }(L_{\tau +1})L_{\tau +1})$, where $\overline{\mu }(L)=\frac{1}{L}\underset{0}{\overset{L}{\int }}\mu (s)\text{d}s$ is the average rate of within-host adaptation over an infection of length L. We then need to un-condition the variables τ and $\stackrel{\rightharpoonup }{L}\equiv (L_1,L_2,\dots ,L_{\tau +1})$ to obtain the probability of emergence

$$P=\underset{\tau }{E}\left[\underset{\stackrel{\rightharpoonup }{L}}{E}\left[1-{(1-u)}^{\tau }\text{exp}\left(-\overline{\mu }(L_1)L_1-\overline{\mu }(L_2)L_2\cdots -\overline{\mu }(L_{\tau +1})L_{\tau +1}\right)|\tau \right]\right].$$ A5

Equation (A 5) is exact, but the mutation rates will typically be small and therefore u and the function μ(s) will be of small magnitude. This can be formalized by viewing u as being composed of some underlying constant multiplied by a small factor, ϵ. Similarly, we can view the function μ(s) as being composed of some underlying (bounded) function of L multiplied by the same small factor, ϵ. Then we can expand expression (A 5) in a Taylor series with respect to ϵ to first-order, giving

$$P=\underset{\tau }{E}\left[\underset{\stackrel{\rightharpoonup }{L}}{E}\left[1-{(1-u)}^{\tau }\text{exp}(-\overline{\mu }(L_1)L_1-\overline{\mu }(L_2)L_2\cdots -\overline{\mu }(L_{\tau +1})L_{\tau +1})|\tau \right]\right]=\underset{\tau }{E}\left[\underset{\stackrel{\rightharpoonup }{L}}{E}[\overline{\mu }(L_1)L_1+\overline{\mu }(L_2)L_2\cdots +\overline{\mu }(L_{\tau +1})L_{\tau +1}+u\tau |\tau ]\right]+o(ϵ)=\underset{\tau }{E}\left[(\tau +1)\underset{\stackrel{\rightharpoonup }{L}}{E}[\overline{\mu }(L)L]+u\tau \right]+o(ϵ)=(\overline{\tau }+1)\underset{\stackrel{\rightharpoonup }{L}}{E}[\overline{\mu }(L)L]+u\overline{\tau }+o(ϵ),$$ A6

where $\overline{\tau }$ is the expected number of transmission events. Standard results from stochastic models of epidemics show that, regardless of the distribution of number of new infections generated by each infected individuals, the expected number of transmission events is $\overline{\tau }=R_0/(1-R_0)$. Consequently, we have $P\approx (1/(1-R_0))(\underset{\stackrel{\rightharpoonup }{L}}{E}[\overline{\mu }(L)L]+u{R}_0)$. If we make the further assumption that there is not much variation in the length of an infection, then this can be further approximated by $P\approx (1/(1-R_0))(\overline{\mu }(L)L+u{R}_0)$ where L is now the typical, average length of an infection. Notice that this result is extremely general, applying to any disease regardless of the pattern of mortality, clearance and transmission during an infection (i.e. it does not rely on the assumption that the transmission and death/clearance rates, b and d respectively, are constant as models 1 and 3 in the text do).