Experimental allometry: effect of size manipulation on metabolic rate of colonial ascidians

Abstract

The allometric scaling of metabolic rate of organisms, the three-quarters power rule, has led to a questioning of the basis for the relation. We attacked this problem experimentally for the first time by employing the modular organism, the ascidian that forms a single layered flat colony, as a model system. The metabolic rate and colony size followed the three-quarters power relation, which held even after the colony size was experimentally manipulated. Our results established that the three-quarters power relation is a real continuous function, not an imaginary statistical regression. The fact that all the hypotheses failed to explain why the two-dimensional organism adhered to the three-quarters power relation led us to propose a new hypothesis, in which the allometric relation derives from the self-organized criticality based on local interaction between modulus-comprising organisms.

1. Introduction

Many biological processes are described by scaling relationships (power law) between two variables: Y=aX^b, where a is the normalization constant and b is the power exponent. When b=1 the relationship is isometric; when b≠1 the relationship is allometric. The three-quarters power law in which the metabolic rate is proportional to 0.75 power of body mass is the most famous and, thus, most studied among the biological allometric scaling rules (Rubner 1883; Hemmingsen 1960; Kleiber 1961; Gould 1966; Peters 1983; Calder 1984; Schmidt-Nielsen 1984). The mechanism that produces this power law has been researched for decades and various hypotheses have been proposed (McMahon 1973; Patterson 1992; West et al. 1997; Banavar et al. 1999). The hypothesis currently prevailing is the one based on the transport network by West, Brown & Enquist (WBE model; West et al. 1997). However, some serious questions were raised against this model from both theoretical and experimental points of view (Alexander 1999; Nakaya et al. 2003; Kozlowski & Konarzewski 2004). The debate on the WBE model was one of the main topics of a recent issue of Functional Ecology where the entire volume was devoted to the discussion of metabolic scaling (Functional Ecology 18, no. 2, 2004).

In spite of continuing efforts, we have not yet established consensus on the metabolic scaling of organisms. We are yet to achieve consensus at several different levels. Most people agree with the presence of ‘universal three-quarters power law’ (West & Brown 2004) but have different opinions on the basis from which the power law emerges. Some people do not agree with the exponent three-quarters. Bokma (2004) claimed, from studies on fishes, that there is no single exponent value that covers all the organisms. Several authors argued that the exponent is not different from the two-thirds proposed from the surface law (Heusner 1982; Dodds et al. 2001; White & Seymour 2003). Heusner (1982) claimed that the three-quarters power relationship was imaginarily derived from statistics. The three-quarters power regression curve has been derived from statistical comparisons of discrete data points from various species and, thus, there is no evidence of a continuous relationship between mass and metabolic rate. This is a fundamental question that has never been answered properly. The direct way to answer this is to experimentally manipulate the body size and see if the metabolic rate shifts after the size manipulation to the value expected from the three-quarters regression line. This experimental method has, however, never been employed because of the difficulty in obtaining body-size changes large enough for statistical analysis, regardless of whether the metabolic rate changed according to three-quarters allometry or isometry.

So far we do not have a good experimental system for metabolic scaling in which size or shape can be artificially manipulated. If we could manipulate such parameters at will, we could design experiments that definitely falsify or support theoretical approaches for, and criticisms of, the three-quarters power law. The manipulation of shape is important because the current theories commonly suppose some dominant structural features that rule over the metabolic rate. The surface area is such a structural feature for the two-thirds power hypothesis (Rubner 1883) and the fractal branching network is for the three-quarters power hypothesis (West et al. 1997). All these features are dependent on the dimension of the body. If we made an organism with a three-dimensional shape into that with a two-dimensional shape, we could test whether the metabolic rate changed according to the hypotheses predicted.

Here we report a system in which size and shape can be manipulated experimentally. We used the colonial ascidian Botrylloides simodensis. This modular organism is a suitable material for studies on allometry for the following reasons (Saito et al. 1981). (i) The colony follows the three-quarters power law. Our previous study (Nakaya et al. 2003) demonstrated that the metabolic rate of B. simodensis is proportional to M^0.799 (M, mass) and that the power coefficient is not different from three-quarters, the exponent for individual organisms, including solitary ascidians (Fisher 1976). (ii) The colony size can be easily manipulated. We can obtain colonies of various sizes by simply dividing a large colony or fusing several little colonies. (iii) The shape of the system is simple: they form a flat single layered colony; thus, effects in the third dimension can be neglected. We can make colonies with various shapes by cutting. (iv) They do not harbour any symbiotic algae and do not produce bony skeletons. (v) The unit that constitutes the system is definite: the full-grown zooids are identical in size and shape, regardless of colony size. (vi) On one hand, the zooids show individual activities and, on the other hand, they are connected to each other by a vascular system and show coordinated behaviour. The presence of a vascular connection is important because West's hypothesis explains the three-quarters power law by vascular networks. The most striking cooperation among zooids can be seen at the time of ‘take over’: all zooids simultaneously give rise to a generation of daughters and the parent generation is absorbed (Watanabe 1953). The take-over occurs once every week. Because of this, the size-manipulated colonies renew themselves within a week, leaving no scars of operation (Hirose et al. 1995).

The size manipulation using colonial ascidians definitely showed that the relation between size and metabolic rate is real, not imaginary. The size manipulation also showed that all current hypotheses fail to explain the results obtained. This leads us to propose a new hypothesis based on self-organized criticality.

2. Material and methods

Colonies of B. simodensis were collected in the vicinity of Nabeta Bay, Shimoda, Shizuoka Prefecture, Japan (Saito et al. 1981). A small colony was put on a thin but tough polyethylene substrate, which was then set in a container hung from a raft in the bay. The colonies spread out on the substrate increasing their size. They were reared for at least two weeks before they were brought into the laboratory. Fouling organisms and detritus were removed from the area of the substrate outside the colony.

Figure 1 is the schematic drawing of colonial ascidian B. simodensis. Botrylloides simodensis reared on a polyethylene substrate made a colony of a simple shape, as in the field. The zooids, approximately 2.0 mm in length and 1.0 mm in width, were arranged in the horizontal plane without overlapping to make a mono-layered sheet-like structure (Saito et al. 1981; Nakaya et al. 2003). The colony surface was smooth and flat. The thickness of the colony was approximately 2.5 mm, irrespective of colony size. The zooids were embedded in a tunic of organic matrix that included several types of cells (Hirose et al. 1995). The tunic, and also zooids, did not harbour symbiotic organisms and did not bear a bony skeleton. Several to several tens of zooids made a ladder system in which the exhalent currents from zooids shared a common drainage that led to a common cloacal aperture. A vascular network evenly spread in the tunic underneath the plane of zooids. Each zooid was connected to the common vascular network by connecting vessels (Mukai et al. 1978). Every colony experienced the phase shift called take-over every week. In the take-over phase, the zooids of the parent generation degenerate and those of the filial generation developed equally and synchronously from a bud state to a full-grown state. All zooids in a colony were thus identical, not only in morphology but also in age (Mukai 1974). We determined the phase of the colony through observation by microscope.

Figure 1.

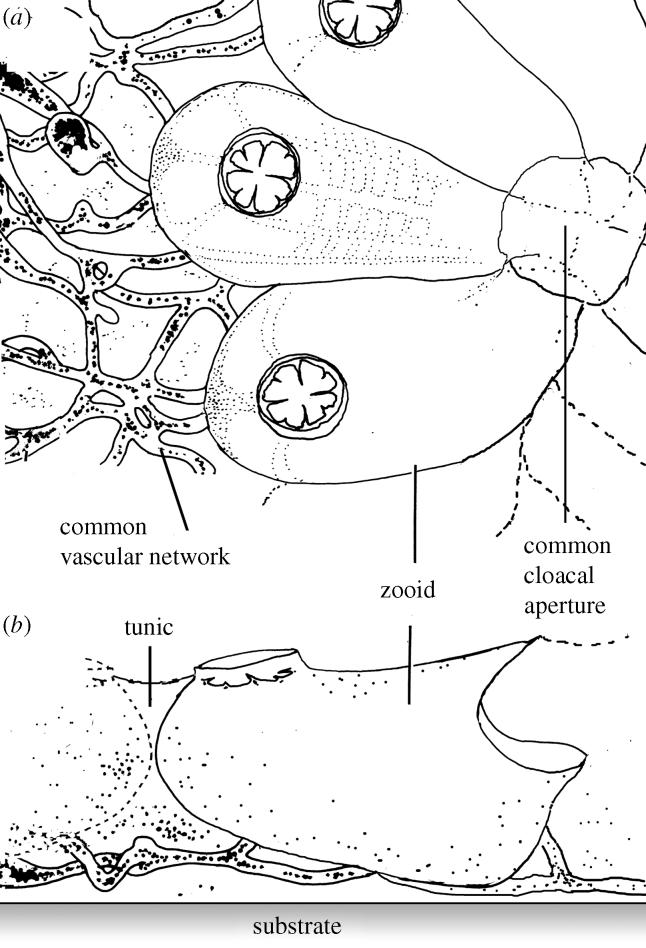
Schematics of the colonial ascidian B. simodensis as seen (a) from above and (b) from side. The common vascular network ran under the zooids, which were removed to show the network (left part of (a); modified from Shirae 2000).

We used genetically identical colonies that originated from a single colony in the size-manipulation experiments. We divided a colony into smaller colonies by cutting it, together with the polyethylene substrate, and reared them for one week for wound healing in the open water. The cut surface was covered with a regenerating cuticular layer within a few hours and the healing was completed within 12 h (Hirose et al. 1995). All the colonies continued to grow well in the sea after division. Since the colonies go through a simultaneous asexual digenetic reproduction process once a week, the wounds, if any, completely disappeared, leaving no scars. We fused 2–4 colonies into one by keeping their edges in contact (Hirose et al. 1997). The tunic cuticles dissolved at the contact area and the vascular ampulla of each colony expanded into their facing colony (Hirose et al. 1997). The ampullae continued penetrating until their tips touched the proximal parts of the ampullae of the facing colony. The ampullae fused and, thus, the vascular vessels of the two colonies fused and the two colonies became a single colony with the same tunic and vascular system. We measured the oxygen consumption of both divided and fused colonies after they had experienced the first generation alternation after the operation.

We used artificial seawater, Mysea (Jamarine, Japan), dissolved in distilled water. The colonies were not fed during the measurement period. To measure the metabolic rate, the colony was acclimatized to experimental conditions in air-saturated artificial sea water (ASW; 33‰ salinity, temperature: 20 °C) for 3 h. The polyethylene substrate to which the colony was attached was placed in an experimental chamber filled with air-saturated ASW. The chamber was placed in a water bath that was maintained at a temperature of 20±0.03 °C (CL-80L, Taitec, Japan). The metabolic rate was measured by the same method as in our previous paper (Nakaya et al. 2003). It was measured by the rate of oxygen consumption using polarographic oxygen electrodes (Model 5300, Yellow Spring Instrument Co., USA). The rates of changes, VO₂, in the dissolved O₂, of the experiments and the controls were calculated using simple linear regression (r²>0.9). The control values were measured every five respiration measurements using the chamber filled with only ASW. The respiration rate per colony was calculated by deducting the control value.

We employed wet weight (M_w) as the variable of the colony size. Our previous study have demonstrated that wet weight (M_w) was proportional to dry weight (M_d; M_w=13.1M_d^1.02 in grams, r²⁼0.990, n=12, 95% confidence interval: 0.960–1.07), and to the number of zooids (N_Z) in a colony (N_Z=418M_w^1.01, r²⁼0.952, n=39, 95% confidence interval: 0.962–1.05); thus, M_w is a convenient and reliable measure of colony size. The M_w was measured as follows: the samples were drained off and were sandwiched between two sheets of tissue paper (KIMWIPE S-2000, Crecia, Japan) whose untouched parts were folded back to wrap around the sample. The samples were thus blotted for 180 s and then weighed with an electric balance. The wet weight of a colony was calculated by deducting the weight of the polyethylene substrate before culturing.

The mass-specific metabolic rates after the manipulation were statistically compared against those before the manipulation. The null hypothesis (that the rates after size manipulation equalled those before the manipulation) was tested using a sign test, where the level of significance was 0.05.

Logarithmic linear regression by a least-squares method gave the following equation:

$$\text{log}{\text{VO}}_2=\text{log}a+b\text{log}{M}_{\text{w}},$$

where VO₂ is oxygen consumption rate, M_w is colonial wet weight, b is the slope of the regression and a, the proportionality coefficient, is the intercept at unity mass. This relation gives the power function VO₂₌a M_w^b. The coefficient a (at 1 g) gives the weight-specific metabolic rate which was used to compare the metabolic activities between species (Schmidt-Nielsen 1984). It should be noted that the specific metabolic rate does not mean the metabolic rate per 1 g, but the metabolic rate of the animal whose body size is 1 g. The 95% confidence interval of the population regression α and β was estimated to test for the regression intercept a and slope b. The following equation was used:

$$\alpha =a\pm t(\text{d}\text{.f}\text{.}=n-2;p=0.05)\times \text{s}\text{.e}{\text{.}}_a,$$

and

$$\beta =b\pm t(\text{d}\text{.f}\text{.}=n-2;p=0.05)\times \text{s}\text{.e}{\text{.}}_b,$$

where d.f. is the degree of freedom, p is critical value and s.e._a and s.e._b are the standard errors of a and b, respectively. The deviation of a constant value from the interval indicates the significant difference (p<0.05). It was also examined to see whether each power coefficient (b) was different from a constant value (b_const). The null hypothesis that each power coefficient (b) equalled a constant value (b_const) was tested using a t-test (H₀: b−b_const=0) with a 0.05 level of significance.

The parameters (a, b) of the regressions of manipulated colonies were statistically compared against those of intact colonies (a_i, b_i), already obtained by our previous study (Nakaya et al. 2003). Null hypothesis that the parameters of manipulated colonies (a, b) equalled those of intact colonies (a_i, b_i) was tested using a t-test (H₀: a−a_i=0, H₀: b−b_i=0) with a 0.05 level of significance.

3. Results

(a) Dividing experiment

Eleven colonies with M_w values ranging from 3.59×10⁻¹ to 1.60 g were used for dividing experiments. Each colony was divided into two to four similar-sized colonies to make 27 colonies in total with M_w values ranging from 6.36×10⁻² to 1.18 g. The metabolic rates of the colonies before division ranged from 1.30×10⁻² to 5.85×10⁻² ml O₂ h⁻¹, and those after division ranged from 4.41×10⁻³ to 5.18×10⁻² ml O₂ h⁻¹ (figure 4a). In figure 2 the changes in colony size represented by the colonial wet weight (M_w), metabolic rate (VO₂), and mass-specific metabolic rate (VO₂/M_w) were shown for each dividing experiment. The filled bar denotes the value of a colony before division and the two to four grey bars right to it denote the values of the colonies created by cutting the colony. The value of M_w of course decreased by division, and so did VO₂ with only one exception. The exceptional case was observed in the colony that experienced the least decrease in the ratio of the change in M_w by division. The mass specific metabolic rate after division, however, increased significantly without exception (sign test, p<0.001, 11 sets 27 pairs).

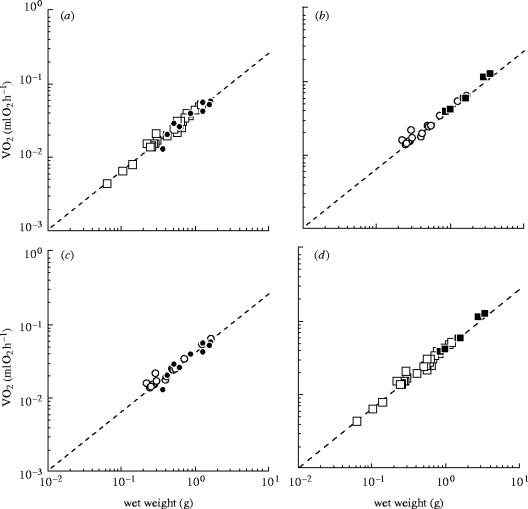
Figure 4.

Oxygen consumption rate plotted against colony size (a, b) and their scaling (c, d). (a) dividing experiment; (b) fusing experiment (c) before size manipulation and (d) after size manipulation. In (c) and (d) data of both dividing experiments and fusing experiments were combined. Filled circles, colonies before division; open squares, colonies after division; open circles, colonies before fusion; filled squares, colonies after fusion. The broken lines denote the allometric relation of intact colonies (VO₂₌0.0412M_w^0.799) reported by Nakaya et al. (2003).

Figure 2.

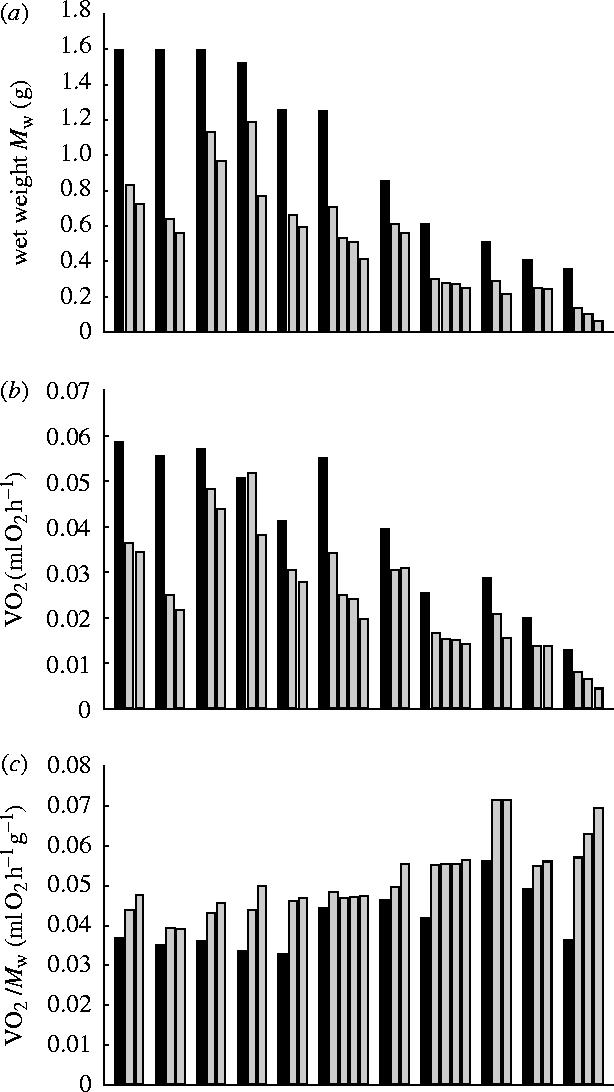
Dividing experiment. (a) wet weight (M_w), (b) oxygen consumption rate (VO₂) and (c) mass specific oxygen consumption rate (VO₂/M_w). Eleven sets of experiments are shown. A filled bar denotes the value of the original colony and the two to four grey bars to the right of the filled bar denote the values of the colonies generated by division of the original colony. Note the VO₂/M_w value increased after division in every set.

(b) Fusing experiment

Sixteen colonies with M_w values ranging from 2.16×10⁻¹ to 1.65 g were used. Two or four colonies were fused to make one colony. The colonies after fusion weighed from 8.56×10⁻¹ to 3.56 g. The metabolic rates of the colonies before fusion ranged from 1.39×10⁻² to 6.43×10⁻² ml O₂ h⁻¹, and those after fusion ranged from 3.95×10⁻² to 1.26×10⁻¹ ml O₂ h⁻¹(figure 4b). Figure 3 shows changes in M_w, VO₂, and VO₂/M_w for each fusing experiment. The filled bar denotes the value of the colony created by fusion and two or four grey bars left to it denote the values of the colonies used in fusion. The value of VO₂ increased without exception after fusion. The mass specific metabolic rates, however, decreased significantly after fusion (sign test, p<0.001, 6 sets 16 pairs).

Figure 3.

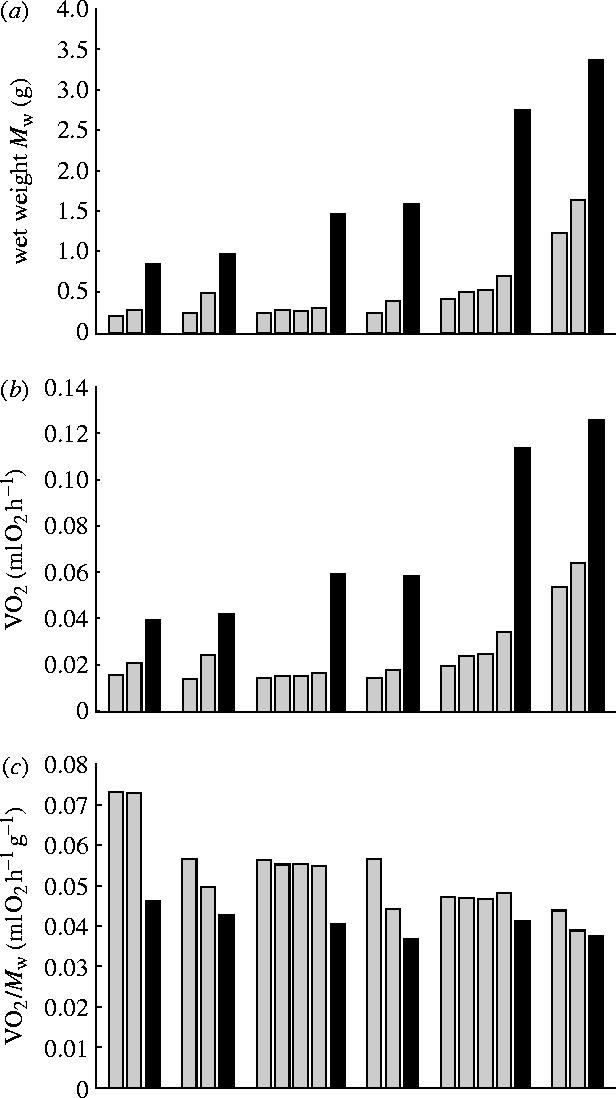
Fusing experiment. (a) wet weight, (b) oxygen consumption rate (VO₂) and (c) mass specific oxygen consumption rate (VO₂/M_w). Six sets of experiments are shown. A filled bar denotes the value of the colony after fusion and the two or four grey bars to the left of the filled bar denote the values of the smaller colonies that were fused together. Note the VO₂/M_w value decreased after fusion in every set.

(c) Scaling of size-manipulated colonies

The metabolic rates of the colonies before size manipulation were plotted against M_w in figure 4c. The plots fell just on the regression line of the intact colonies of this species VO₂=0.0412M_w^0.799 (Nakaya et al. 2003) that was obtained from the dataset with much broader M_w range and larger sample number (M_w: 2.86×10⁻²–4.10 g; n=60). A statistically significant regression line could be generated from the present plots. The allometric relationship thus obtained was VO₂=0.0407M_w^0.751 (r²=0.946, n=27, 95% confidence of coefficients; a, 0.0382–0.0435 and b, 0.677–0.825). This relationship was not different from that of Nakaya et al. (confidence parameter a; t=0.0120, p=0.990, slope b; t=0.0570, p=0.955).

The metabolic rates of dividing experiments were plotted against M_w in figure 4a and those of fusing experiments in figure 4b. The plots after size manipulation fell just on the regression line of Nakaya et al. (2003) obtained for intact colonies (figure 4d). The data of the dividing experiments and the fusing experiments were combined and the regression of the metabolic rates after size manipulation was calculated. The size-manipulated colonies gave the statistically significant regression line VO₂=0.0441M_w^0.828 (r²=0.983, n=33, 95% confidence of coefficients; a, 0.0422–0.0460 and b, 0.788–0.868). This relationship did not differ significantly from that of intact colonies of Nakaya et al. (confident parameter a; t=0.0854, p=0.932, slope b; t=0.0439, p=0.997). The regression lines were calculated from each dataset of the colonies before division, after division, before fusion, and after fusion, and the lines were compared with the regression line of the intact colonies of Nakaya et al. 2003 (table 1). None of the lines were statistically different from the intact colonies, which implied that the metabolic rates before size-manipulation and after size-manipulation, irrespective of division or fusion, belonged to the same population as the intact colonies did.

Table 1.

Regression lines of VO_2.

	n	coefficient	slope	statistical difference from intact colony
a	b	a		b
t	p	t	p
before size manipulation	27	0.0407	0.751	0.0120	0.990	0.0570	0.955
after size manipulation	33	0.0441	0.828	0.0854	0.932	0.0439	0.997
before division	11	0.0394	0.825	0.0357	0.972	0.0126	0.990
after division	27	0.0437	0.819	0.0686	0.945	0.0286	0.977
before fusion	16	0.0426	0.770	0.0321	0.975	0.0316	0.975
after fusion	6	0.0427	0.898	0.0231	0.982	0.0441	0.965
intact colony (Nakaya et al. 2003)	60	0.0411	0.799	—	—	—	—

4. Discussion

Our experiments clearly showed that the size-manipulated colonies adapt their metabolic rate to their new body size according to the three-quarters power rule. The largest colony after fusion was 53 times larger than the smallest colony after division. The size range of nearly two orders was large enough to obtain a reliable regression line. We thus succeeded, for the first time in the long history of studies of the three-quarters-power rule, in developing a model system whose size can be manipulated experimentally. Although this system is a colony, the prevailing hypotheses, both classic and modern, such as the surface law and the WBE model (West et al. 1997), do not distinguish between colonial and unitary organisms. Thus, we could test the generality of these hypotheses with the present system.

With this system we could also consider the two fundamental reservations regarding the widely accepted view that the exponent three-quarters is real and different from two-thirds, the value that the surface rule predicts. Heusner (1982) claimed that the three-quarters is a statistical artefact. He supposed that the intraspecific exponent is two-thirds and that the three-quarters power relation is an imaginary one extracted from the dispersive data points from different species. The reliable value for the intraspecific exponent is, however, difficult to obtain because the range of adult body sizes is quite narrow. With our system we could show that the intraspecific exponent for the colony is close to three-quarters (Nakaya et al. 2003) and, thus, is not different from interspecific exponents. Our experiment showed that the size-manipulated colonies just fell on the regression line of intact colonies, which implies our data points are not dispersive but continuous. Our experiment thus established for the first time that the metabolic rate is, in fact, a dependent variable for the weight as the independent variable, which has been taken for granted without experimental justification in the long history of scaling studies.

Dodds et al. (2001) showed, using sophisticated statistical methods, that the measured three-quarters value is not statistically different from two-thirds. This is a fundamental discussion that cannot be circumvented if we use the organisms whose surface area is proportional to two-thirds power of body mass. In our system of colonial ascidians, however, the surface area is proportional to the body mass because the colony grows two dimensionally (Nakaya et al. 2003) and yet the exponent is close to three-quarters, rather than 1 (the value surface law predicts for two-dimensional organisms). This is clear evidence that the three-quarters power law cannot be attributed to the surface area only.

The colonies we made by division and fusion took various shapes in a two-dimensional plane. And yet the metabolic rate of all the colonies fell on a single regression line. This provided evidence against the hypotheses that assume special relations between the parameters of external shape, such as the elastic similarity hypothesis (McMahon 1973). Our results suggest that the factors that determine the external shape of organisms may not be indispensable for producing the three-quarters power law.

Both the surface law and the elastic similarity hypothesis are based on the classic geometry concept and rely on the scaling of the external structure of the body. The recent hypothesis, however, paid attention to the internal structure of the body (West et al. 1997). The discussion of West et al. used geometry extended to non-whole number dimensions (Mandelbrot 1982). If some internal structure dominating the rate of energy consumption has a dimension of 2.25, the three-quarters coefficient can be theoretically derived. The model based on this theoretical framework is the WBE model (West et al. 1997). The authors showed that the network of mammals' blood vessels has a fractal branching pattern and they skilfully connected this fact with the three-quarters power law. Their network was, however, a hierarchical fractal with a single root. The colonial ascidians in the present study do not have such a hierarchical fractal-like network. Their network of vessels is a simple mesh-like system in which uniform units were connected locally with each other. The WBE model predicts that the organisms with such a mesh-like network will show isometric scaling and that two-dimensional organisms with hierarchical branching will show the two-thirds power scaling. Our system, however, showed an exponent close to three-quarters that is different from 1 and from two-thirds. Thus, our system cast doubt upon the generality of the area-preserving branching model.

The hypotheses so far proposed have pursued some structure, external or internal, that has a dominant effect on the metabolic rate. The failure of these hypotheses to explain our results led us to take an entirely different approach. The colony of B. simodensis is a discrete system made of uniform units with local interaction: zooids are of the same size and shape with no differentiation in their role in the colony and are connected to each other by vessels that make a diffuse network. We have discovered that the metabolic scaling switched from allometry to isometry when the connection between zooids disappeared (Nakaya et al. 2003). This suggests that it is the local interaction that produces metabolic allometry. Unitary organisms could also be regarded as a discrete system composed of similar sized modules, namely cells, with local mutual interaction (Vogel 1988). This macroscopic view of the animal body has allowed us to treat the metabolic allometry as a phenomenon in statistical mechanics. When a system is made of identical units with local interaction, criticality can be produced spontaneously (Bak et al. 1987). It should be noted that if the discrete system with local interaction shows allometry, the system is dynamic not static. In the static state, the behaviour of the units is described by an exponential function of size, not by a power function. The power law is the sign of criticality in the dynamic system because the critical phenomena are defined by the divergence of the integral of the power function (Goldenfeld 1992). Several studies suggested that some biological phenomena are associated with criticality (Gisiger 2001; Torres 2001). Usual critical phenomena, such as boiling and melting, are not stable. However, it has been known that some criticalities of discrete systems can be produced and maintained spontaneously (Bak et al. 1987; Goldenfeld 1992). The ascidian colonies seem to be such a system because they spontaneously kept the allometric relation, even when their size was disturbed. The size manipulation suggests that spontaneous criticality is maintained by self-organization. One basis for this idea was the question of how each zooid could ‘know’ the colony size. The adult ascidians have no image-making eyes and no tentacles long enough to feel the whole colony. The colony has no centre of sensing and decision-making that orders the zooids to follow a certain rule. Yet each zooid changed its metabolic rate as if it ‘knew’ the size of the colony it was in and the amount of energy it should consume. If the ascidian colony is the system keeping the criticality through self-organization, the allometric relation is maintained after size manipulation, even if the zooids have no organs to sense the colony size and the colony has no sensing and decision-making centre.

The hypothesis that self-organized criticality is the source of allometry is a general hypothesis that may be applicable to both unitary organisms and colonial organisms. It is also applicable to unicellular organisms if a cell can be regarded as an assembly of some functional units. We hypothesize that criticality through self-organization played a key role in the evolution of organisms. The organisms with larger sizes appeared later in the history of both unicellular and multicellular organisms' evolution. When the system becomes larger, and thus the number of units increases, the chance of the units' activities becoming uneven in the system increases. This may impair the stability of the system. The system with self-organized criticality, however, can keep the activities of units even without elaborate controlling structures. Thus, it seems reasonable to suppose that the organisms with self-organized criticality had more chance of survival in the early stages of evolution. The local interaction described by a power function has no limit in the distance between the interacting units and, thus, the system with such an interaction can increase its size indefinitely, without changing the power relation (Bak et al. 1987). These systems without size limits possess a scale invariance. It was suggested that systems with a scale-free network have high tolerance to random errors (Réka et al. 2000). These features seem to be of great merit in the early metazoan evolution.

The self-organized criticality hypothesis explains why the metabolic activities of wide varieties of organisms follow the power function. We hypothesize that the power three-quarters was adopted by the first organism with self-organized criticality; once the system started with one particular exponent, it would have been quite difficult to change it. The number three-quarters might well have been selected by chance. Otherwise our hypothesis suggests that the reason three-quarters was selected should be explored in the first organism with self-organized criticality, not in the well developed organisms prospering today. Our hypothesis does not exclude, however, the WBE model because it is possible that vertebrates later developed the circulatory system with a fractal-like branching pattern that secures the power relation inherited from ancestors. With that system, they may have acquired the freedom to differentiate units of body organs into various sizes and functions.