Fuzzy Logic in Medicine and Bioinformatics

Abstract

The purpose of this paper is to present a general view of the current applications of fuzzy logic in medicine and bioinformatics. We particularly review the medical literature using fuzzy logic. We then recall the geometrical interpretation of fuzzy sets as points in a fuzzy hypercube and present two concrete illustrations in medicine (drug addictions) and in bioinformatics (comparison of genomes).

INTRODUCTION

The diagnosis of disease involves several levels of uncertainty and imprecision, and it is inherent to medicine.

A single disease may manifest itself quite differently, depending on the patient, and with different intensities. A single symptom may correspond to different diseases. On the other hand, several diseases present in a patient may interact and interfere with the usual description of any of the diseases.

The best and most precise description of disease entities uses linguistic terms that are also imprecise and vague. Moreover, the classical concepts of health and disease are mutually exclusive and opposite. However, some recent approaches consider both concepts as complementary processes in the same continuum [1–6]. According to the definition issued by the World Health Organization (WHO), health is a state of complete physical, mental, and social well-being, and not merely the absence of disease or infirmity. The loss of health can be seen in its three forms: disease, illness, and sickness.

To deal with imprecision and uncertainty, we have at our disposal fuzzy logic. Fuzzy logic introduces partial truth values, between true and false.

According to Aristotelian logic, for a given proposition or state we only have two logical values: true-false, black-white, 1-0. In real life, things are not either black or white, but most of the times are grey. Thus, in many practical situations, it is convenient to consider intermediate logical values. Let us show this with a very simple medical example. Consider the statement “you are healthy”. Is it true if you have only a broken nail? Is it false if you have a terminal cancer? Everybody is healthy to some degree h and ill to some degree i. If you are totally healthy, then of course h = 1, i = 0. Usually, everybody has some minor health problems and h < 1, but

$$h+i=\mathrm{1\; .}$$ (1)

In the other extreme situation, h = 0, and i = 1 so that you are not healthy at all (you are dead). In the case you have only a broken nail, we may write h = 0.999,i = 0.001; if you have a painful gastric ulcer, i = 0.6,h = 0.4, but in the case you have a terminal cancer, probably i = 0.95, h = 0.05. As we will see, this is a particular case of Kosko's hypercube: the one-dimensional case [4].

Uncertainty is now considered essential to science and fuzzy logic is a way to model and deal with it using natural language. We can say that fuzzy logic is a qualitative computational approach.

Since uncertainty is inherent in fields such as medicine and massive data in bioinformatics, and fuzzy logic takes into account such uncertainty, fuzzy set theory can be considered as a suitable formalism to deal with the imprecision intrinsic to many biomedical and bioinformatics problems. Fuzzy logic is a method to render precise what is imprecise in the world of medicine. Several examples and illustrations are mentioned below.

FUZZY LOGIC IN MEDICINE

The complexity of medical practice makes traditional quantitative approaches of analysis inappropriate. In medicine, the lack of information, and its imprecision, and, many times, contradictory nature are common facts. The sources of uncertainty can be classified as follows [7].

1. Information about the patient.

2. Medical history of the patient, which is usually supplied by the patient and/or his/her family. This is usually highly subjective and imprecise.

3. Physical examination. The physician usually obtains objective data, but in some cases the boundary between normal and pathological status is not sharp.

4. Results of laboratory and other diagnostic tests, but they are also subject to some mistakes, and even to improper behavior of the patient prior to the examination.

5. The patient may include simulated, exaggerated, understated symptoms, or may even fail to mention some of them.

6. We stress the paradox of the growing number of mental disorders versus the absence of a natural classification [8]. The classification in critical (ie, borderline) cases is difficult, particularly when a categorical system of diagnosis is considered.

Fuzzy logic plays an important role in medicine [7, 9–14]. Some examples showing that fuzzy logic crosses many disease groups are the following.

1. To predict the response to treatment with citalopram in alcohol dependence [15].

2. To analyze diabetic neuropathy [16] and to detect early diabetic retinopathy [17].

3. To determine appropriate lithium dosage [18, 19].

4. To calculate volumes of brain tissue from magnetic resonance imaging (MRI) [20], and to analyze functional MRI data [21].

5. To characterize stroke subtypes and coexisting causes of ischemic stroke [1, 3, 22, 23].

6. To improve decision-making in radiation therapy [24].

7. To control hypertension during anesthesia [25].

8. To determine flexor-tendon repair techniques [26].

9. To detect breast cancer [27, 28], lung cancer [28], or prostate cancer [29].

10. To assist the diagnosis of central nervous systems tumors (astrocytic tumors) [30].

11. To discriminate benign skin lesions from malignant melanomas [31].

12. To visualize nerve fibers in the human brain [32].

13. To represent quantitative estimates of drug use [33].

14. To study the auditory P50 component in schizophrenia [34].

15. Many other areas of application, to mention a few, are

    1. to study fuzzy epidemics [35],
    2. to make decisions in nursing [36],
    3. to overcome electroacupuncture accommodation [37].

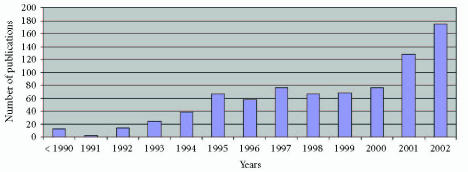
We used the database MEDLINE to identify the medical publications using fuzzy logic. We used as keywords fuzzy logic and grade of membership. The total number of articles per year appears in Table 1. The data is from 1991 to 2002 and includes also the number of those publications in 1990 and before. It results in a total of 804 articles and agrees essentially with the numbers indicated in [7, 13]. We plan to screen databases in the engineering literature that covers medicine-related articles since it is difficult to publish medical results using a fuzzy logic approach. In the future we will compare the figures obtained.

Table 1.

Number of papers per year in medicine using fuzzy logic.

Year	Number
≤1990	13
1991	2
1992	14
1993	24
1994	38
1995	66
1996	58
1997	76
1998	66
1999	68
2000	76
2001	128
2002	175

Figure 1 indicates an exponential growth in the number of articles in medicine making use of fuzzy technology. The preliminary data we have for 2003 and 2004 [38] supports this tendency.

Figure 1.

Number of publications per year indexed in MEDLINE using fuzzy logic.

FUZZY LOGIC IN BIOINFORMATICS

Bioinformatics derives knowledge from computer analysis of biological data. This data can consist of the information stored in the genetic code, and also experimental results (and hence imprecision) from various sources, patient statistics, and scientific literature. Bioinformatics combines computer science, biology, physical and chemical principles, and tools for analysis and modeling of large sets of biological data, the managing of chronic diseases, the study of molecular computing, cloning, and the development of training tools of bio-computing systems [39]. Bioinformatics is a very active and attractive research field with a high impact in new technological development [40].

Molecular biologists are currently engaged in some of the most impressive data collection projects. Recent genome-sequencing projects are generating an enormous amount of data related to the function and the structure of biological molecules and sequences. Other complementary high-throughput technologies, such as DNA microarrays, are rapidly generating large amounts of data that are too overwhelming for conventional approaches to biological data analysis. We have at our disposal a large number of genomes, protein structures, genes with their corresponding expressions monitored in experiments, and single-nucleotide polymorphisms (SNPs) [41]. For example, the EMBL Nucleotide Sequence Database (http://www.ebi.ac.uk/embl) has increased in 12 months from 18.3 million entries comprising 23 Gb (Release 71, September 2002) to 27.2 million entries comprising over 33 Gb (Release 76, September 2003) as indicated in [42].

Handling this massive amount of data, in many cases imprecise and fuzzy, requires powerful integrated bioinformatics systems and new technologies.

Fuzzy logic and fuzzy technology are now frequently used in bioinformatics. The following are some examples.

1. To increase the flexibility of protein motifs [43].

2. To study differences between polynucleotides [44].

3. To analyze experimental expression data [45] using fuzzy adaptive resonance theory.

4. To align sequences based on a fuzzy recast of a dynamic programming algorithm [46].

5. DNA sequencing using genetic fuzzy systems [47].

6. To cluster genes from microarray data [48].

7. To predict proteins subcellular locations from their dipeptide composition [49] using fuzzy k-nearest neighbors algorithm.

8. To simulate complex traits influenced by genes with fuzzy-valued effects in pedigreed populations [50].

9. To attribute cluster membership values to genes [51] applying a fuzzy partitioning method, fuzzy C-means.

10. To map specific sequence patterns to putative functional classes since evolutionary comparison leads to efficient functional characterization of hypothetical proteins [52]. The authors used a fuzzy alignment model.

11. To analyze gene expression data [53].

12. To unravel functional and ancestral relationships between proteins via fuzzy alignment methods [54], or using a generalized radial basis function neural network architecture that generates fuzzy classification rules [55].

13. To analyze the relationships between genes and decipher a genetic network [56].

14. To process complementary deoxyribonucleic acid (cDNA) microarray images [57]. The procedure should be automated due to the large number of spots and it is achieved using a fuzzy vector filtering framework.

15. To classify amino acid sequences into different superfamilies [58].

THE FUZZY HYPERCUBE

In 1992, Kosko [4] introduced a geometrical interpretation of fuzzy sets as points in a hypercube. In 1998, Helgason and Jobe [1] used the unit hypercube to represent concomitant mechanisms in stroke. Indeed, for a given set

$$X=\{x_1,\dots ,x_n\},$$ (2)

a fuzzy subset is just a mapping

$$\mu :X\to I=[0,1],$$ (3)

and the value μ(x) expresses the grade of membership of the element x ∈ X to the fuzzy subset μ.

For example, let X be the set of persons of some population and let the fuzzy set μ be defined as healthy subjects. If John is a member of the population (the set X), then, μ (John) gives the grade of healthiness of John, or the grade of membership of John to the set of healthy subjects. If λ is the fuzzy set that describes the grade of depression, then λ (Mary) is the degree of depression of Mary.

Thus, the set of all fuzzy subsets (of X) is precisely the unit hypercube Iⁿ = [0, 1]ⁿ, as any fuzzy subset μ determines a point P ∈ Iⁿ given by $P=(\mu (x_1),\dots ,\mu (x_n))$. Reciprocally, any point $A=(a_1,\dots ,a_n)\in I^n$ generates a fuzzy subset μ defined by μ(x_i) = a_i, $i=1,\dots ,n$. Nonfuzzy or crisp subsets of x are given by mappings $x:X\to \{0,1\}$, and are located at the 2ⁿ corners of the n-dimensional unit hypercube Iⁿ. For graphic representations of the two-dimensional and three-dimensional hypercube, we refer to [59].

Given,

$$p=(p_1,p_2,\dots ,p_n),$$$$q=(q_1,q_2,\dots ,q_n)\in I^n$$ (4)

, not both equal to the empty set not both equal to the empty $\varnothing \text{=(0,0,}\dots \text{,0)}$, we define the difference between p and q as

$$d(p,q)=\frac{{\sum }_{i=1}^n\left|p_i-q_i\right|}{{\sum }_{i=1}^n\max \{p_i,q_i\}\; .}$$ (5)

Of course d( ∅, ∅) = 0. We know that d is indeed a metric [60]. Hypercubical calculus has been described in [61], while some biomedical applications of the fuzzy unit hypercube are given in [1, 6, 59]. Recently, the fuzzy hypercube has been utilized to study differences between polynucleotides [59] and to compare genomes [44, 62].

AN APPLICATION TO DRUG ADDICTIONS

We now present an example of the use of the fuzzy hypercube in a medical case of consumption of drugs.

Consider the following fuzzy variables: smoking and alcohol drinking. If you do not smoke, then your degree of being a smoker is evidently 0. If you smoke, for example, six cigarettes per day, we say that your degree of being a smoker is 0.8. If the consumption is ten or more, the degree is 1. See [63 Figure 3.8] for a geometrical representation of the fuzzy concept of being a smoker.

With respect to the other fuzzy variable, if you drink no alcohol, the degree of this variable is 0. If you drink more than 75 cc of alcohol per day, the degree of alcoholism is 1. For 25 cc/d, the degree could be 0.4 and for 50 cc/d, 0.8.

Thus, the fuzzy set μ = (0, 0) corresponds to a nonsmoker and teetotaler. Some further examples are the following: the set μ = (1, 0) represents a heavy smoker, but a teetotaler, and the set μ = (0.8, 1) is a person who smokes about six cigarettes a day and is a risk consumer of alcohol.

Suppose you correspond to the fuzzy set λ = (1, 1), have recently had some health problems, and your physician has advised you to reduce your consumption of cigarettes and alcohol by half. The ideal situation for your health is, of course, the point μ = (0, 0), but it is possibly difficult to achieve.

Cigarette smoking and alcohol drinking during adolescence have been shown to be associated with a greater possibility of concurrent and future substance-related disorders (Lewinsohn etal [64]; Nelson and Wittchen [65]). In order to report patterns of drug use and to describe factors associated with substance use in adolescents, a cross-sectional survey was carried out in a representative population sample of 2550 adolescents, aged 12 to 17 years, from Galicia (an autonomous region located in the Northwest of Spain). The original survey covered the use of alcohol, tobacco, illicit drugs, and other psychoactive substances. For tobacco smoking and alcohol drinking, each subject of the population sample was assigned a fuzzy degree of addiction (or risk use) and mapped into the two-dimensional hypercube I² by an expert.

Several subjects occupy the same point in the two-dimensional hypercube. For example Figure 2 represents the number of subjects in the cross-sectional survey according to the two fuzzy degrees of addiction. The reader can see that there are 1278 subjects corresponding to the point (0,0), that is, nonsmoker and teetotaler. Also 7 adolescents are at the point (0.8,0.2). There are 121 subjects on the line of probability x₁ + x₂ = 1. Indeed (see Figure 2), 23 + 1 + 1 + 2 + 2 + 7 + 1 + 84 = 121.

Figure 2.

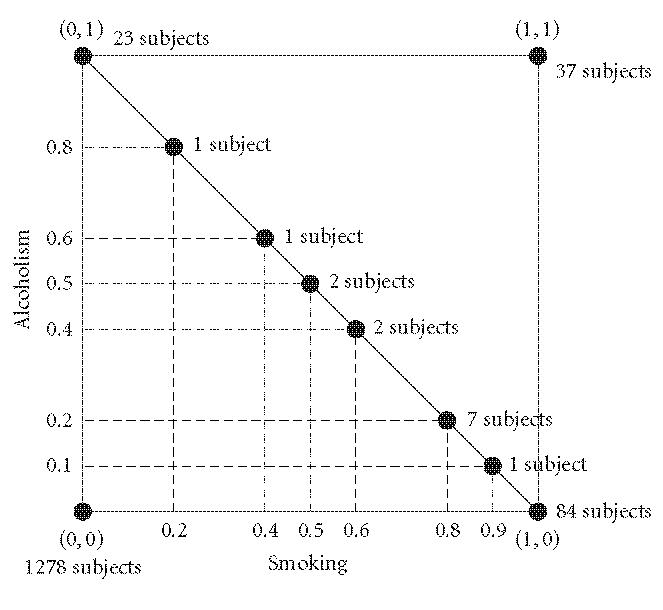
Number of subjects in the two-dimensional fuzzy hypercube I².

Most subjects were inside the hypercube but outside the line of probability. This means that the vast majority of subjects ($2429/2550\approx 95.25\%$) are outside the line of probability. This is in agreement with the fundamental limitation of probability theory with respect to clinical science in general [1] and agrees with its results ($29/30\approx 96.66\%$).

We refer to [59] for details on the general theory of fuzzy midpoints and their applications. It has been used recently to average biopolymers [66].

AN APPLICATION TO THE COMPARISON OF GENOMES

Whole genome sequence comparison is important in bioinformatics [44, 67].

The complete genome sequence of Mycobacterium tuberculosis H37Rv is available at http://www.ncbi.nlm.nih.gov with accession number NC_–000962.

The genome comprises 4 411 529 base pairs, contains around 4000 genes, and has a very high guanine+cytosine content [68]. Computing [44] the number of the nucleotides at the three base sites of a codon in the coding sequences of M tuberculosis (Table 2), and then calculating the corresponding fractions, we have the fuzzy set of frequencies of the genome sequence of M tuberculosis (Table 3). This set can be considered as a point in the hypercube I¹². Indeed, the point

$$\begin{array}{l}\text{(0}\text{.1632, 0}\text{.3089, 0}\text{.1724, 0}\text{.3556, 0}\text{.2036, 0}\text{.3145, }\\ \text{0}\text{.1763, 0}\text{.3056, 0}\text{.1645, 0}\text{.3461, 0}\text{.1593, 0}\text{.3302)}\in {\text{I}}^{\text{12 .}}\end{array}$$ (6)

Table 2.

Number of nucleotides at the three base sites of a codon in the coding sequence of Mycobacterium tuberculosis.

	T	C	A	G
First base	216 051	409 011	228 244	470 868
Second base	269 638	416 457	233 472	404 607
Third base	217 803	458 256	210 892	437 223

Table 3.

Fractions of nucleotides at the three base sites of a codon in the coding sequence of Mycobacterium tuberculosis.

	T	C	A	G
First base	0.1632	0.3089	0.1724	0.3556
Second base	0.2036	0.3145	0.1763	0.3056
Third base	0.1645	0.3461	0.1593	0.3302

Aquifex aeolicus was one of the earliest diverging, and is one of the most thermophilic, bacteria known [69]. It can grow on hydrogen, oxygen, carbon dioxide, and mineral salts. The complex metabolic machinery needed for A aeolicus to function as a chemolithoautotroph (an organism which uses an inorganic carbon source for biosynthesis and an inorganic chemical energy source) is encoded within a genome that is only one-third the size of the E coli genome.

The corresponding data for A aeolicus was obtained from http://www.ncbi.nlm.nih.gov with accession number NC_000918, and is presented in Tables 4 and 5, respectively. The complete genome sequence has 1 551 335 base pairs. The fuzzy set of frequencies of the genome of A aeolicus is

$$\begin{array}{l}\text{0}\text{.1706, 0}\text{.1605, 0}\text{.3241, 0}\text{.3446, 0}\text{.3282, 0}\text{.1735, }\\ \text{0}\text{.3478, 0}\text{.1504, 0}\text{.2139, 0}\text{.2455, 0}\text{.3052, 0}\text{.2352)}\in {\text{I}}^{\text{12 .}}\end{array}$$ (7)

Table 4.

Number of nucleotides at the three base sites of a codon in the coding sequence of Aquifex aeolicus.

	T	C	A	G
First base	82 722	77 800	157 096	167 050
Second base	159 068	84 092	168 591	72 917
Third base	103 692	119 016	147 956	114 004

Table 5.

Fractions of nucleotides at the three base sites of a codon in the coding sequence of Aquifex aeolicus.

	T	C	A	G
First base	0.1706	0.1605	0.3241	0.3446
Second base	0.3282	0.1735	0.3478	0.1504
Third base	0.2139	0.2455	0.3052	0.2352

Using the distance given in (5), it is possible to compute the distance between these two fuzzy sets representing the frequencies of the nucleotides of A aeolicus and M tuberculosis:

$$d(\mathrm{A aeolicus, M tuberculosis})=\frac{2.2125}{6.106}\approx \mathrm{0.3623\; .}$$ (8)

In [44] we calculate the difference between M tuberculosis and E coli K-12 obtaining

$$d(\mathrm{M tuberculosis, E coli})=\frac{\text{0}\text{.8506}}{\text{3}\text{.4253}}\approx \text{0}\text{.2483 .}$$ (9)

Using the corresponding data for E coli (see [44 Tables 3 and 3]), we get

$$d(\mathrm{A aeolicus, E coli})=\frac{\text{0}\text{.8514}}{\text{5}\text{.0161}}\approx \text{0}\text{.1697 .}$$ (10)