A ratio model of perceived speed in the human visual system

Abstract

The perceived speed of moving images changes over time. Prolonged viewing of a pattern (adaptation) leads to an exponential decrease in its perceived speed. Similarly, responses of neurones tuned to motion reduce exponentially over time. It is tempting to link these phenomena. However, under certain conditions, perceived speed increases after adaptation and the time course of these perceptual effects varies widely. We propose a model that comprises two temporally tuned mechanisms whose sensitivities reduce exponentially over time. Perceived speed is taken as the ratio of these filters' outputs. The model captures increases and decreases in perceived speed following adaptation and describes our data well with just four free parameters. Whilst the model captures perceptual time courses that vary widely, parameter estimates for the time constants of the underlying filters are in good agreement with estimates of the time course of adaptation of direction selective neurones in the mammalian visual system.

1. Introduction

Given that the early stages of visual processing are relatively well understood, it is surprising that there is no consensus as to how the human visual system encodes the speed of a moving image. There are at least three classes of model that have attempted to characterize this fundamental property of vision: first, motion energy models (we include here also gradient and Reichardt approaches which may be differently motivated but are formally equivalent to motion energy models; Adelson & Bergen 1985; van Santen & Sperling 1985; Watson & Ahumada 1985), second, response frequency models (Barlow & Hill 1963; Clifford & Langley 1996; Bex et al. 1999) and most recently, Bayesian models of speed perception (Ascher & Grzywacz 2000; Hurlimann et al. 2002; Weiss et al. 2002). None of these models can capture what we know about how perceived speed may vary following adaptation to a moving pattern.

Motion energy models assume that non-directional spatiotemporal filters are added and subtracted in quadrature pairs to create direction selective units. A squaring of the units' outputs ensures a smooth response and a differencing of left and right sensitive units gives an unambiguous directional, but not speed, signal. This class of model confounds velocity and contrast and, although scaling the detector's output by some ‘static’ detector's response (Adelson & Bergen 1986) would eliminate contrast dependence, the motion energy model does not concern itself with how an ensemble of detectors might encode speed. Clearly an array of ‘motion detectors’ each tuned to a different speed might be envisaged but such a ‘labelled lines’ approach to speed encoding is not consistent with much of what we know about human speed perception. For instance, adaptation to a moving stimulus reduces the perceived speed of that stimulus and all slower speeds in the same direction and may increase the perceived speed of faster stimuli (Carlson 1962; Clymer 1973; Thompson 1981; Smith & Edgar 1994). Similarly, reducing the contrast of a slowly moving pattern reduces its perceived speed (Thompson 1982; Stone & Thompson 1992; Hawken et al. 1994). These findings do not point towards a ‘place’ or labelled lines model of speed in which the output of an ensemble of narrowly tuned overlapping channels determines speed (Heeger 1987; Grzywacz & Yuille 1990). Nor do they fit well with the Bayesian class of models that assume that a prior will ‘distort’ our estimate of speed. Whilst this class of model can account for distortions in one direction, e.g. reductions in perceived speed, they cannot simultaneously predict both increases and decreases in perceived speed that are contingent upon prevailing viewing conditions without the invocation of a somewhat arbitrary second prior.

Another approach, which we term the Response Frequency model, has been to postulate that speed is encoded in the frequency of response of direction-selective mechanisms (Barlow & Hill 1963). This approach envisages a ‘frequency’ code similar to that assumed to underlie contrast coding. Such a proposal readily explains the reduction in perceived speed of patterns following adaptation in a fashion analogous to Blakemore et al.'s (1973) model of contrast adaptation. Recently, a number of studies have attempted to elucidate the nature and function of speed adaptation by measuring the time course of its effects (Clifford & Langley 1996; Bex et al. 1999). The decay of perceived speed as a function of adaptation duration has been found to be well fit by a simple exponential model of the reduction of spike rates in cat cortical cells after motion adaptation (Giaschi et al. 1993). Upon the basis of these findings it has been proposed that the exponential decay of spike rates may form the neural substrate for motion adaptation. This suggestion has a long history and offers a potentially powerful model for many perceptual phenomena (Sutherland 1961; Barlow & Hill 1963) but in its simplest form this model struggles to explain well established phenomena. For instance, how could observed increases in speed following adaptation (Carlson 1962; Rapoport 1964; Clymer 1973; Thompson 1981; Smith & Edgar 1994) be explained? Moreover, whilst a large range of time courses for perceptual decay in perceived speed has been found (Clifford & Ibbotson 2002), physiological estimates of reduction in spike rates converge on a much smaller range (Maddess & Laughlin 1985; Giaschi et al. 1993; Ibbotson & Mark 1996). The solution to these problems may lie in a ratio model of speed encoding for which there is much psychophysical evidence (Harris 1980; Thompson 1982; Harris 1986; Smith & Edgar 1994).

We have previously measured speed adaptation and its subsequent recovery and have shown that decreases in perceived speed after adaptation were consistent with a ratio model of perceived speed (Hammett et al. 2000). Here we report the results of a parametric study of perceived speed as a function of adaptation duration, test and adaptation speed. We measured the perceived speed of sinusoidal gratings that drifted over a wide range of speeds after adapting to a moving grating for one of six adaptation durations. Six adaptation speeds were investigated with adaptation gratings always moving in the same direction as the test gratings. In order to ensure that contrast adaptation did not confound adaptation to speed per se (Blakemore et al. 1973; Thompson 1981; Hammett et al. 1994) we ensured that the contrast of adapting patterns was much lower than that of the test patterns. We show that both the increases and decreases in perceived speed observed in these psychophysical measurements are well described by a model that assumes speed is encoded as the ratio of two temporal filters whose sensitivities decay exponentially over time.

2. Material and Methods

(a) Apparatus and stimuli

All stimuli were horizontally oriented sinusoidal gratings generated on a VSG 2/3W (Cambridge Research Systems) waveform generator and displayed on an EIZO 6600-M Monochrome monitor. The monitor was gamma corrected using the CRS OPTICAL photometric system. Mean luminance was 32 cd m⁻² and the frame rate was 100 Hz. The active display subtended 30°×24° and the gratings were presented in circular windows (diameter=6°) situated such that the inner edge was 1° to the left (adapting patterns) or 1° to the right (test patterns) of a small dark fixation spot. The spatial frequency was always 1 c °⁻¹ and the test and adapting patterns drifted upwards at one of a range of speeds (2–20° s⁻¹). The stimuli were windowed with sharp edges in both space and time. The adapting contrast was 10% and the test contrast was 50%. The viewing distance was 57 cm.

(b) Procedure

At the beginning of each trial two stimuli were presented simultaneously for 500 ms. The subjects' task was to indicate which of the two patterns (left or right) appeared faster by pressing a button. An adapting pattern was subsequently presented to the left of the central fixation point for each of five durations (4, 8, 16, 32 or 64 s). Following adaptation the adapting stimulus was replaced with a blank field of mean luminance for 10 ms. Subsequently two stimuli were presented simultaneously for 500 ms. A standard pattern was located in the original position of the adapting pattern, and a test pattern, whose speed was controlled by a modified PEST procedure (Taylor & Creelman 1967) was located to the right of the fixation point. The subject indicated which pattern appeared faster after each presentation. The speed of the test patterns was altered by independent PEST procedures that were set to converge on the 50% point using six interleaved staircases. After each such run subjects rested for at least 2 min in order to minimize build up of adaptation. Thirty such runs were taken and the 50% point of the resultant psychometric function was estimated by Probit (Finney 1971). The mean of four such estimates was taken as the point of subjective equality.

The experiments were conducted binocularly in a semi-darkened room with no head restraint. One of the subjects was naive to the purpose of the experiment, the other was aware of the general purpose of the experiment. Both subjects were experienced psychophysical observers.

3. Results

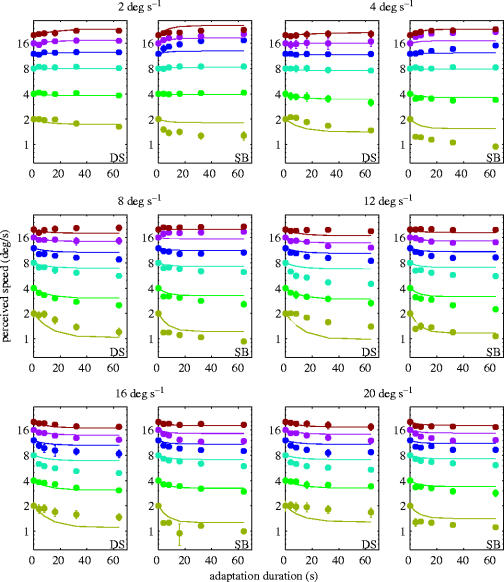
The results (along with the best fit of the model described below) are shown in figure 2. For the higher adaptation speeds (>12° s⁻¹), the effect of adaptation was to reduce perceived speed at all test speeds (2–20° s⁻¹). Perceived speed reduced quasi-exponentially as a function of adaptation duration. This is in good agreement with previous psychophysical studies (e.g. Bex et al. 1999; Hammett et al. 2000). However, for the lower adaptation speeds (2 and 4° s⁻¹), the effect of adaptation depended upon test speed. At low-test speeds, adaptation resulted in a reduction in perceived speed similar to that observed for high adaptation speeds. However, under conditions where adaptation speed was low (2 and 4° s⁻¹) and test speed was higher (>8° s⁻¹) perceived speed increased quasi-exponentially as a function of adaptation duration. Whilst no such increase as a function of time has been reported before, the basic effect of an increase in speed under such conditions is well documented (Thompson 1981). Thus the psychophysical data indicate that adaptation can lead to both increases and decreases in perceived speed depending upon adapt and test speeds and that these effects take a quasi-exponential form. In the following section we develop a simple ratio model, based upon physiologically plausible temporal filters, in order to capture these characteristics of speed perception.

Figure 2.

Perceived speed (solid symbols) as a function of adaptation duration and the best fit of the model (solid lines). Each panel represents the results for one adaptation speed (indicated above the graph). Each test speed is represented by a different colour. The results for each subject (SB and DS) are shown separately. Error bars represent ±s.e.m.

(a) The model

The model assumes that perceived speed is based upon the ratio of a low-pass and band-pass temporal filter. The model employs the filters recently proposed by Perrone (2005). These filters provide a good fit to typical tuning functions in macaque V1. The low-pass filter takes the form

$$p(\omega )=\sqrt{a^2+b^2},$$ 3.1

where

$$a={({(2\pi \omega {\tau }_1)}^2+1)}^{-(9/2)}\text{and}b={({(2\pi \omega {\tau }_2)}^2+1)}^{-(10/2)},$$

and the band-pass filter is given by

$$m(\omega )=\frac{\omega }{k}p(\omega ),$$ 3.2

where ω is temporal frequency. Following Perrone, we have used values of 0.0072, 0.0043 for the time constants (measured in seconds) τ₁ and τ₂, respectively. The parameter k is set to 4. We have adhered to Perrone's convention of labelling the low-pass and band-pass filters p and m, respectively. As noted by Perrone, a simple ratio of m(ω)/p(ω) is proportional to ω, a desirable feature of a speed encoding mechanism. Note that there are no free parameters at this stage of the model. Figure 1a shows the filter sensitivities for these parameter values. The filter sensitivities are determined by an additive combination of the two low-pass filters, a and b, the features of which are in turn determined by the time constants τ₁ and τ₂. Due to the differences in time constants used here, the upper limb of p(ω) is dominated by the component b. For frequencies greater than ${(2\pi {\tau }_2)}^{-1}$ (i.e. 37 Hz) the expression tends to ${(2\pi \omega {\tau }_2)}^{-10}$ and thus tends to a slope of −10 on a log–log plot. The component, a, plays its role on the lower limb of the combined filter p(ω) by controlling the corner frequency (i.e. the frequency at which response is attenuated 3 dB). For the filters used here the corner frequency is 8 Hz. For the band-pass filter, m(ω), upper and lower limbs are similarly dominated by the terms a and b. The term k scales the filter's response. For the parameter values used here, peak response of m(ω) is at 10.8 Hz.

Figure 1.

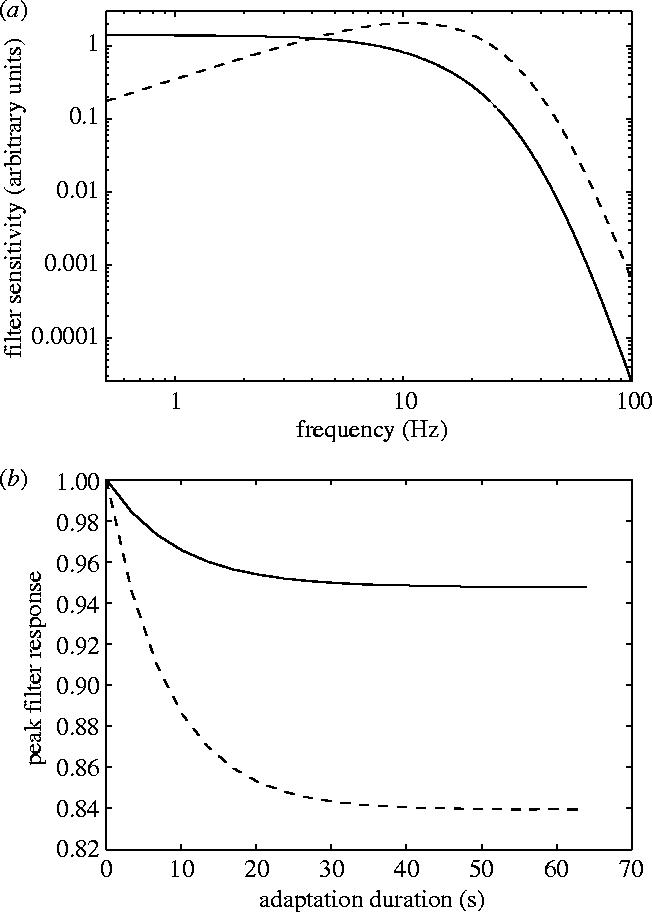
(a) The filter sensitivities for p (solid line) and m (broken line) are shown. (b) The decay of peak filter response as a function of adaptation duration is illustrated for cases of near-optimal adaptation (i.e. at values of ω_a close to peak filter sensitivity). The decay functions have been normalized with respect to peak filter response. The decay functions are shown for p (solid line) at ω_a=2 Hz and for m (broken line) at ω_a=12 Hz using the best fit of the model to data averaged over both subjects.

The model comprises four free parameters that determine the time constants of exponential decay and asymptotic response attenuation for the low-pass and band-pass filters. Thus the filters' sensitivities decay over time such that their responses as a function of speed and time are given by:

$$P(\omega ,t)=p({\omega }_{\psi })-K_{p}p({\omega }_a)\left\{1-{\text{e}}^{-t/T_p}\right\},$$ 3.3

$$M(\omega ,t)=m({\omega }_{\psi })-K_{m}m({\omega }_a)\left\{1-{\text{e}}^{-t/T_m}\right\},$$ 3.4

where ω_a and ω_ψ are the adaptation and test frequencies, respectively, and t is adaptation duration measured in seconds. The free parameters T_p and T_m are the time constants, measured in seconds, of the adaptation dependent reduction in filter sensitivities. The other free parameters K_p and K_m determine the magnitude of the reduction in the filters' sensitivities resulting from adaptation, that is the maximum (asymptotic) response attenuation. Thus the model assumes that filter sensitivities will decay exponentially over time by an amount determined by the product of the free parameter K_p (or K_m) and a term that reflects the relative sensitivity of the filter to the adaptation frequency p(ω_a). Figure 1b illustrates how the peak responses of these filters decrease for the case where adaptation frequency is near the peak sensitivity of the respective filters. For the case ω_a=ω_ψ a value of unity for K_p or K_m could result in zeroing the filter's response as t tends to infinity. Although K_p and K_m were not constrained in the model fitting, it was anticipated that they would lie between 0 and 1 so as to limit the effect of adaptation on the filter responses to plausible values.

Perceived speed S is given by the ratio of the output of these two filters such that:

$$S=\frac{M(\omega ,t)}{P(\omega ,t)}.$$

In order to estimate the time constants and saturation levels of the filters we found the best-fitting values of these free parameters using an error minimization function (fminsearch) in Matlab 7.0.1 (Mathworks Inc). The resultant best fits (solved for all adaptation speeds, test speeds and adaptation durations simultaneously) are shown in figure 2, alongside the psychophysical data.

The psychophysical estimates of perceived speed in the absence of adaptation (at t₀) were near veridical (the average standard error was within 4.2% of the physical speed). However, in order to avoid the model fit being biased by measurement error at t₀ perceived speed for each condition was scaled to be veridical at t₀ and this scaling factor was subsequently applied to all other points within the condition. This is equivalent to constraining the model fit such that perceived speed is veridical in the absence of adaptation. The model parameters for the best fits for each subject are shown in table 1. The time constants are in good agreement with those reported for the decay in response of single directionally selective neurones in the cat cortex (Giaschi et al. 1993; around 5–8 s) and our previous estimates of the underlying filters' time constants (Hammett et al. 2000; 8 and 7.25 s for T_p and T_m, respectively). The model captures the essential characteristic of both increases and decreases in perceived speed, contingent upon the adapt–test relationship. The model captures both increases and decreases in perceived speed because p may decrease proportionately more or less than m as a function of adaptation duration. Overall, the model captures around 96% of the variance of the data (table 2). There are, however, a few conditions where the fits are less adequate. These tend to be at moderate test speeds (8 and 12° s⁻¹). However, even here, the lowest r² value is 0.42 and is typically much higher than that. Encouragingly, these less adequate fits are not confined to the same conditions across subjects and it seems reasonable to assume that the lower r² values are a reflection of the transitional nature of these conditions. Note that whilst low adaptation speeds (e.g. 2 and 4° s⁻¹) yield increases in perceived speed at high test speeds, high adaptation speeds (e.g. 16 and 20° s⁻¹) yield reductions in perceived speed. Thus, the model must render a point of inflection at some intermediate speed in order to capture both effects. The model does this smoothly but tends to miss the subjects' actual point of inflections. Given this, and the fact that the model still adequately fits all conditions, it seems reasonable to assume that the lower r² values for these conditions is attributable to ‘under-constraining’ the model with respect to the point of inflection rather than to a systematic error in the model.

Table 1.

Model parameters for the best fits for each subject.

parameter	DS	SB
Tp	13.42	6.31
Tm	10.26	6.15
Kp	0.05	0.06
Km	0.18	0.15

Table 2.

r² values for the model fit for each test speed and overall fit at all test speeds.

test speed (° s−1)	DS	SB
2	0.9979	0.9983
4	0.9988	0.9971
8	0.8507	0.9404
12	0.4225	0.6149
16	0.9785	0.8950
20	0.9842	0.9796
overall	0.9774	0.9616

4. Discussion

Previous researchers have suggested that the neural substrate for decreases in perceived speed may be the decrease in single unit activity of cells sensitive to motion (Barlow & Hill 1963; Clifford & Langley 1996; Bex et al. 1999). Whilst this approach has intuitive appeal, it fails to account for the increases in perceived speed after adaptation that is reported here and elsewhere (Thompson 1981). Similarly, whilst motion energy models have been highly successful at describing how direction of motion may be computed, they require a ‘labelled line’ approach to speed encoding that is not consistent with much psychophysical data. Furthermore, it is not clear how they should account for increases in perceived speed. A final class of model that uses Bayesian priors (e.g. Hurlimann et al. 2002) to explain reductions in perceived speed under certain circumstances should also have difficulty in accommodating both increases and decreases in speed after adaptation without assuming that the prior can change.

The present results indicate that perceived speed is exquisitely sensitive to prevailing viewing conditions and can increase or decrease over time, depending upon previously seen speeds. The time course of these velocity after-effects is well described by an exponential function, regardless of whether perceived speed increases or decreases over time. These findings are in agreement with previous psychophysical studies that have measured a much more limited range of adaptation speeds and durations. Around 96% of the variance in our data can be resolved by a simple ratio model of perceived speed that has only four free parameters that control the time constants and asymptotic response attenuation of a low-pass and a band-pass temporal filter. The filters are consistent with the temporal tuning properties of cortical cells in the macaque (Foster et al. 1985; Hawken et al. 1996) and bear a close resemblance to those suggested by Anderson & Burr's (1985) psychophysical study. The time constants of the best fitting model are consistent with the empirically derived time constants reported for the decay in response of single cortical neurones in the cat (Giaschi et al. 1993). Furthermore, psychophysical estimates of the time constants of adaptation vary widely, from 1 to 16 s (Clifford & Ibbotson 2002), depending upon stimulus parameters. In the present study, our more extensive psychophysical estimates of perceived speed yielded time constants for best fitting exponentials over an even greater range (from 2 to 46 s for conditions where perceived speed reduced). Despite these wide differences in time constants for the perceptual phenomenon, estimates of the model's filter time constants are very similar to the estimates obtained for single cells whilst their ratio simultaneously captures the wider ranging psychophysically derived time constants. Thus the model captures large changes in perceptual dynamics with physiologically plausible and stable underlying filter dynamics.

We conclude that a model that employs physiologically plausible temporal filters and that assumes that speed is encoded as the ratio of the output of those filters adequately captures many of the characteristics of perceived speed with just four free parameters. The question of what may constitute the neural substrate of these filters is clearly of great interest. It has not escaped our notice that Perrone (2005) labelled his low-pass and band-pass filters p and m, respectively, and that both parvo- and magno-cellular pathways appear to be implicated in the creation of direction selective cells in V1(DeValois et al. 2000). However, the very different contrast gain (Kaplan & Shapley 1986; Sclar et al. 1990), and presumably adaptation, properties of the two pathways may mitigate against such a scheme. We are currently investigating whether the ratio of magno- and parvo-cellular responses may be implicated in the computation of object speed.