Influence of density dependence on predator–prey seabird interactions at large spatio-temporal scales

Abstract

Theoretical investigations of competitive dynamics have noted that numbers of predator and prey influence each other. However, few empirical studies have demonstrated how a life-history trait of the prey (such as fecundity) can be affected simultaneously by its own density and the density of predators. For instance, density dependence can reduce fecundity with increasing number of prey, while inverse density dependence or Allee effects may occur especially when the prey is a social organism. Here we analysed an intraguild predator–prey system of two seabird species at a large spatio-temporal scale. As expected, we found that fecundity of prey was negatively affected by predator density. Nevertheless, fecundity of prey also increased nonlinearly with its own density and strikingly with the prey–predator ratio. Small groups of prey were probably not able to defend their nests especially against large number of predators. At the highest prey densities (i.e. when anti-predator strategies should be most efficient), prey fecundity also lowered, suggesting the appearance of density dependence mediated by food competition. Allee effects and density dependence occurred across a broad range of population sizes of both the prey and the predator at several local populations facing different ecological environments.

1. Introduction

Predator–prey models have received a great deal of interest in different fields of science, from evolutionary and behavioural ecology to conservation and population biology and even economics (e.g. Quentin-Grafton & Silva-Echenique 1997). The first theoretical framework developed under the Malthus–Verhuslt logistic theory treated single species population dynamics, and was followed by the first models of trophic (predator–prey) interactions by Lotka and Volterra. More recently, and evolving from logistic theory, several attempts have been made to model predator–prey dynamics incorporating ratio-dependent functional responses (Berryman 1992; Ginzburg & Akçakaya 1992). A keystone assumption of ecological theory is that densities of both prey and predator are forcedly influencing their population dynamics. For instance, density dependence on predation rates is expected when predator densities attain the carrying capacity (e.g. Lande et al. 2003). At the opposite end, smaller groups of prey may be more exposed to predation than larger groups (inverse density dependence, or Allee effect; Crawley 1992; Courchamp et al. 1999; Stephens & Sutherland 1999). In general, several mechanisms can lead to a reduction in population growth rate at small population sizes, including difficulties in finding mates, poorer defence against predators and lower foraging efficiency (e.g. Engen et al. 2003). Although Allee effects have been shown theoretically, there are few empirical data, mostly coming from species with cooperative breeding and broadcast spawning (Gascoigne & Lipcius 2004). Yet, theoretical models of predator–prey interactions have been tested with observational data mainly using organisms with short generation times and rapid dynamics, especially invertebrates from aquatic ecosystems, while terrestrial studies come mainly from cyclic dynamics (e.g. Cappuccino & Price 1995). Data are even scarcer when predator and prey share the same ecological guild, even though it has been recently recognized that potentially competing species engaged in predator–prey interactions can contribute greatly to community structure (Ives et al. 2005). Here we analysed a simple predator–prey system composed of two top-level marine predators in which one (yellow-legged gull, Larus michahellis) is a facultative predator on the other (Audouin's gull, Larus audouinii). Prey fecundity depends not only on food availability, but also on nest predation rates (e.g. Oro et al. 1999). Previous studies of this predator–prey relationship have already suggested that changes in the densities of not only the predator, but also that of the prey, could influence prey fecundity through changes in nest predation rates (Oro 1996; Oro et al. 1996). For instance, some behavioural studies (Oro & Martínez-Vilalta 1994; Martínez-Abraín et al. 2003a) showed that small groups of prey could be more exposed to predation, owing to a combination of two factors: a small number of conspecifics to collaborate in nest defence, and a high ratio of perimeter/colony size, which exposes a relatively larger number of nests to access by predators. We explore the appearance of density dependence and Allee effects by analysing whether fecundity of prey was influenced by its own density, by predator densities and by the ratio between them, using long-term data from four different local populations (i.e. colonies) with different ecological features.

2. Material and methods

(a) The focal species and the study area

The two species of syntopic gulls share most of their life-history traits and the main difference is the facultative predation exerted by yellow-legged gulls on eggs and chicks of Audouin's gulls. The yellow-legged gull is almost exclusively the sole predator for Audouin's gull nests (Oro et al. 1999). Other forms of interaction can also affect prey fecundity in an indirect way, such as competition for food at foraging grounds and kleptoparasitism (Oro & Martínez-Vilalta 1994; Arcos et al. 2001).

The local populations under study were those of the Columbretes Islands (39°54′ N, 00°41′ E), Alboran Island (35°56′ N, 3°02′ W), Chafarinas Islands (35°11′ N, 3°46′ E) and the Ebro Delta (40°33′ N, 0°39′ E), all in the western Mediterranean. The main differences among populations are their ecological features: Columbretes and Alboran are small (19 and 7 ha, respectively) and have limited foraging grounds owing to their oceanographic characteristics (ca 55 km from the mainland) with a relatively small available foraging area of continental shelf. The Ebro Delta is at the opposite extreme, with a much larger patch (2500 ha) and with very large foraging grounds, while Chafarinas is an intermediate case in surface area (50 ha) and feeding opportunities. This also explains why total numbers of breeders (of predator and prey together) were much lower at Alboran and Columbretes than at Chafarinas and especially than at the Ebro Delta (figure 1). Densities of predator and prey (as number of breeding pairs) and prey fecundity were estimated through standard methods already tested in our study sites over the years (e.g. Oro & Ruxton 2001; Martínez-Abraín et al. 2003b,c).

Figure 1.

Density of predators (breeding females of L. michahellis, open circles) and prey (breeding females of L. audouinii, solid circles) and prey fecundity (dashed line refers to second y-axis) of four different local populations: (a) Columbretes, (b) Alboran, (c) Chafarinas and (d) Ebro Delta. All time-series end in 2004 but they begin when all the three parameters were available, the first year being different in each local population. Prey fecundity has the same scale for the four populations, but not population density, which is different in each case.

(b) Statistical treatment and biological hypotheses

We used a generalized linear mixed model to analyse the relationship between prey fecundity (noted Pf) and density of both prey and predator, and the ratio between the two densities. This allowed us to introduce explicative variables that could be correlated, such as the densities of both predator and prey (expressed in the models as Pd and Py, respectively, see below) in space and time. Since the dependent variable Pf did not follow a normal distribution (Shapiro–Wilk test=0.847, d.f.=62, p<0.0001), we carried out a square root transformation, which is appropriate in our case of variance increasing as the mean increases. This is especially true because our sample was considered as taken from a Poisson distribution. Transformation was performed using the equation

$$P{f}^{\prime }=\sqrt{Pf}+\sqrt{Pf+1},$$

which has good variance-stabilizing qualities for variables such as fecundity, with values ranging from 0 to 2 (see figure 1; Shapiro–Wilk test on Pf′=0.969, d.f.=62, p=0.118). Because of the temporal stochastic nature of fecundity, we corrected for the year term by introducing it as a random effect. This precluded a goodness-of-fit test of the models, but comparisons of their deviances with the null model yielded small discrepancies (see electronic supplementary material). Potential autocorrelation in densities and fecundities was not taken into account, because the temporal autocorrelations in the study populations are weak, due to the extremely high and stochastic emigration–immigration rates among populations (Oro & Ruxton 2001; Oro et al. 2004). We reduced the test of interactions between factors to avoid overparameterized models and in turn the non-convergence of deviance profiles or the unreliability in parameter estimators.

To explore the underlying patterns between prey fecundity and density of both prey and predator, we plotted the variables and fit a robust locally weighted regression smoothing surface using a lowess method by iteration of weighted least squares (Simonoff 1996). Following this exploratory analysis (see §3), we tested not only for linear correlations between prey fecundity and the explanatory variables, but also for nonlinear effects between prey fecundity and population density of both prey and predator (e.g. Courchamp et al. 1999), by including nonlinear functions (such as quadratic and logarithmic; see figure 2). These models were based on the type II and type III behavioural patterns described first by Holling (1959) on predator–prey interactions (see also Berryman 1992 for ratio-dependent functional responses). For instance, the quadratic function of prey density (denoted as Pf²) would suggest an Allee effect (or inverse density dependence) on prey fecundity before the appearance of density dependence. This type of function, with higher values of fecundity at intermediate population densities, was what Allee (1931) found in his original study on social inhibition of breeding, and it was similar to the type III functional response. We also tested whether the fecundity curve changed monotonically with density to an asymptote (S-shaped—or sigmoid—and logarithmic forms, similar to the type III and type II functional responses, respectively; see figure 2).

Figure 2.

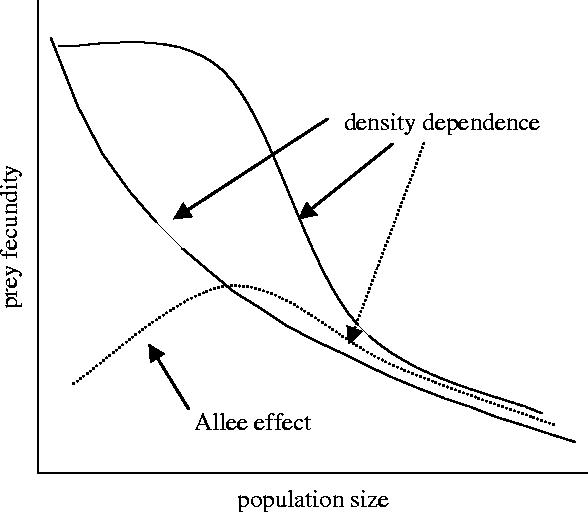
Illustration of several biological hypotheses modelled in our analysis: the solid lines show density dependence of prey fecundity with population size (the predator and prey densities together) with a logarithmic and logistic shapes; the dashed line shows an inverse density dependence at low prey numbers (Allee effect) before the appearance of density dependence at higher population sizes. Several mathematical models were fitted to each hypothesis (see §2).

The significance of the main effects and interactions was assessed by comparing models with or without the effects tested, in interaction or additive manner. Although many theoretical models have employed the ratio of the predator and prey, we only tested this factor in combination with at least one of the two actual variables (Jasienski & Bazzaz 1999). When using the ratio, either of the two variables (densities of both prey and predator) is no longer identifiable, so the use of at least one of them is statistically and biologically sensitive. Model selection was made on the basis of Akaike's Information Criterion adjusted for small sample sizes (AICc).

3. Results

The results shown in figure 3 suggest that prey fecundity changed following a pattern depending on densities of both prey and predator. Maximum values of fecundity occurred with the lowest densities of predators, while fecundity seemed to show a quadratic relationship with the density of prey, i.e. the highest values were found at intermediate prey density levels. In fact, the combinations of the two factors (lowest predator densities together with intermediate prey densities) yielded the highest fecundity values (figure 3). Fecundity also decreased nonlinearly with increasing predator density although a slight increase occurred at relatively high prey density values. Modelling confirmed some of these trends (table 1, see electronic supplementary material). The finally selected model (model 1) actually showed a logarithmic and statistically significant relationship between prey fecundity and densities of both prey (positive trend: t=6.455, d.f.=46.9, p<0.0001) and predator (negative trend: t=−5.614, d.f.=49.5, p<0.0001). Furthermore, fecundity increased significantly as the ratio between density of prey and density of predators increased (t=2.188, d.f.=45.8, p<0.01). Other associations between the dependent and explicative variables (linear—such as models 5–7—and nonlinear, including quadratic—such as models 8, 9, 13 and 19—and logarithmic—such as models 10 and 16—as interactions or additive) did not result in more parsimonious models (table 1 in the electronic supplementary material). In general, the addition of the colony effect yielded similar values of AICc than the models without the effect (e.g. model 1 versus model 2, model 8 versus model 9). This was also true for the finally selected model: adding a colony effect resulted in a statistically equivalent model (model 2 in table, see electronic supplementary material). Coefficients of this model suggested that the nonlinear association between prey fecundity and densities of prey and predators and their ratio was more pronounced at the smallest local populations (Columbretes and Alboran). In these populations, failures of prey fecundity were regular (more than 30% of the years, see figure 1a,b), and breeding seemed to succeed only above a threshold of prey densities determined by a ratio of 1 : 1 with predators (figure 4). In the larger colonies (Ebro Delta and Chafarinas), prey fecundity was less variable for the whole ranges of densities of prey and predator, which were well above that threshold of 1 : 1 (see figure 4 and also figure 1c,d). The logarithmic relationship found in figure 4 confirmed the results of the modelling (see above). Below this threshold, prey fecundity was significantly lower than above the 1 : 1 ratio (U Mann–Whitney test=101.0, p<0.0001).

Figure 3.

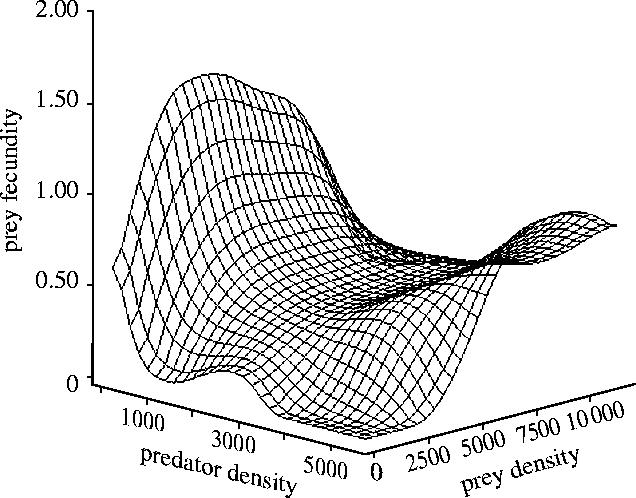
Smoothing regression surface of the relationship between prey fecundity (measured as number of fledglings per breeding female) and density of both prey and predator (both as number of breeding females). All the data available (actual variable values for all years and local populations) were used. Note than even though the regression surface covers all the range of predator and prey densities, predators and prey were always present in the study (see figure 1).

Figure 4.

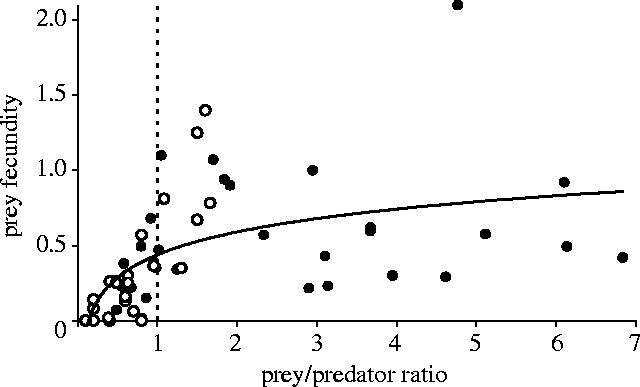
Association between prey fecundity and the ratio prey/predator for the four-study local populations. Open circles show the relationship for the smaller populations (Columbretes and Alboran) and solid circles the relationship for the larger populations (Ebro Delta and Chafarinas). The solid line shows the logarithmic relationship between the two variables for the pooled data, which was statistically significant (F=60.8, d.f.=59, p<0.0001). The dashed line shows the threshold below which predator population was larger than prey population (see text).

4. Discussion

An emergent feature of the present study was the prediction of Allee effects across a broad range of population sizes of both the prey and the predators and at a large spatial scale, within several local populations facing different ecological environments. Allee effects resulted in lower prey fecundity with low prey densities, whatever the density of predator recorded. Yet, breeding failures occurred always below a threshold of prey/predator 1 : 1 ratio, which occurred especially in the smaller prey populations under study (see also Martínez-Abraín et al. 2003b). Allee effects were actually stronger in these populations, but even here they could be slight when predator densities were low. Allee effects also appeared with low densities of predator (see figure 3) and here low fecundity could be more influenced by lower social foraging enhancement (Arcos et al. 2001). A demographic Allee threshold can influence colony extinction probability, which in Audouin's gull can be mediated (at least partially) by the Allee threshold on breeding failures found here (see also Martínez-Abraín et al. 2003a). An additional Allee effect below the threshold of breeding failure may result in high emigration and low immigration depensatory rates at metapopulation level through conspecific attraction from much larger prey populations, where predation is lower and, in turn, fecundity is higher (Holyoak & Lawler 1996; Oro et al. 2004). The relationship between prey fecundity and density of both prey and predators presented here followed similar stochastic patterns than the per capita population growth rate in non-deterministic population dynamic models after the incorporation of Allee effects (e.g. Cappuccino & Price 1995; Courchamp et al. 1999; Lande et al. 2003; Taylor & Hastings 2005). These models show that population growth rate is highest at intermediate population sizes, and that Allee effects preclude small populations from performing better. One of the mechanisms underlying an Allee effect was social facilitation (Allee 1931). Conspecific facilitation against predators had already been recorded in Audouin's gull and other colonial birds where anti-predator strategies become inefficient in small groups (e.g. Oro 1996; Brunton 1999; Brown & Brown 2001; Cuthbert 2002).

Study populations were also affected by density dependence on prey fecundity. Fecundity was actually higher at intermediate prey densities, and then lowered. At the highest prey densities, fecundity was likely to be more constrained by competition for food although several studies have shown that predation still occurred (Oro & Martínez-Vilalta 1994; Martínez-Abraín et al. 2003b). Density dependence on prey fecundity was probably affected not only by intraspecific but also by interspecific competition for food resources (Brown & Brown 2001). Again, results suggested that density dependence was stronger in the smaller populations, with a lower number of foraging habitats available (Oro et al. 1996; Ruiz et al. 1998; Oro & Pradel 2000; Oro & Ruxton 2001; Genovart et al. 2003). Higher prey fecundities were actually recorded in the largest prey populations (figure 1c,d), where predator densities were actually lower and thus the prey/predator ratio was the highest. The stabilization of prey fecundity with the increase in population density (prey and predators together) is probably enhanced by an increase of predation rates that occurs when food-mediated density dependence appears. For instance, new fishing policies will reduce an important foraging resource (i.e. fishing discards) in seabird communities, and would affect intraguild predator–prey systems and their relationships in time and space. Under this scenario, it is expected that facultative predators, in the absence or lowering of the main food, would increase predation rates and population dynamics of smaller sympatric species, some of them with a conservation concern (Votier et al. 2004).