Dispersal is not female biased in a resource-defence mating ungulate, the European roe deer

Abstract

Dispersal is frequently more prevalent in one sex compared to the other. Greenwood proposed that patterns of sex-biased dispersal among birds and mammals are linked to their mating strategies. For species where males defend resources rather than females, he predicted female-biased dispersal, because males should remain at their birth site where they are familiar with the distribution of the resources that they must defend. Greenwood's hypothesis has been extensively supported among birds, where most species exhibit a resource-defence mating strategy. However, almost no equivalent information is available for mammals as males generally defend mates in this group. An exception is the European roe deer, a resource-defence mating ungulate. We thus tested Greenwood's hypothesis on this atypical mammalian model, looking for female-biased dispersal using sex-specific inter-individual genetic distances. We conclusively show that gene flow is not higher among females compared to males in the studied roe deer population, and hence that dispersal is not female-biased, suggesting that male mating strategy is not the primary selective force driving the evolution of dispersal in roe deer. We discuss the role of female mate choice and intra-sexual competition as possible alternative selective pressures involved.

1. Introduction

Dispersal is a universal phenomenon which refers to the movement of an organism from its birth place to its first breeding site (natal dispersal) or from one breeding site to another (breeding dispersal; Shields 1987). A considerable amount of research has focused on the evolution of this behaviour, either from reviews of empirical data (e.g. Greenwood 1980; Waser & Jones 1983; Moore & Ali 1984; Wolff 1993; Lambin et al. 2001), or with a modelling approach (e.g. Gandon 1999; Perrin & Mazalov 1999, 2000; Perrin & Goudet 2001). In particular, these studies focused on understanding why dispersal is frequently more prevalent in one sex compared to the other. Indeed, among mammals, most species show male-biased dispersal, whereas in birds, dispersal is predominantly female-biased (Greenwood 1980).

Greenwood (1980) proposed that patterns of sex-biased dispersal among birds and mammals are linked to their mating strategies. In a resource-defence strategy, which occurs in most birds, males defend a resource which is of primary importance to females. Under this scenario, females choose their mate in relation to this resource, which may be important for rearing offspring and/or an indicator of the owner's quality. Greenwood supposed that philopatric males may acquire and defend this resource more easily than dispersing males, due to their better local knowledge of the site; thus, males would benefit from being philopatric, while females should disperse in order to avoid inbreeding. In a mate-defence strategy, which is typical of the majority of mammals, males do not need to express site-specific dominance, they compete directly for access to females; female distribution thus determines male dispersal behaviour, and males are thus expected to disperse more than females. This prediction is quite well supported by the available empirical data (e.g. Favre et al. 1997), with certain exceptions (Waser & Jones 1983; e.g. yellow-bellied marmots: resource-defence polygyny and male-biased dispersal), and by mathematical models (Perrin & Mazalov 1999, 2000; Perrin & Goudet 2001).

Greenwood (1980) noted that he was not able to test his hypothesis of female-biased dispersal in resource-defence strategy ungulates due to the lack of information on dispersal in this group. This situation still persists, as most ungulate species where males defend resources are located in Africa (Owen-Smith 1977) and to date little information is available on their dispersal patterns. In contrast to most ungulates of the northern hemisphere, the European roe deer (Capreolus capreolus), a medium-sized species, widely spread across Europe, exhibits resource-defence polygyny (Liberg et al. 1998): males defend a territory which overlaps with the home range of one or more females with whom they may mate, but they do not defend females themselves. Hence the roe deer provides a unique case in which to test Greenwood's hypothesis.

In this species, offspring share their mother's home range until their first spring, when they may either settle in a home range contiguous and/or overlapping with their mother's range, or disperse. Natal dispersal is sometimes delayed, mainly for males, until their second spring (Linnell et al. 1998). There is no breeding dispersal in roe deer as adults generally remain faithful to their home range from one year to the next (Danilkin & Hewison 1996; but see §4). Despite a large number of intensive studies on this species, few data on sex-specific patterns of dispersal are available (see Linnell et al. 1998). Conclusions based on observations of marked or radio-tracked animals are hampered by small sample size and a variable pattern, with little or no sex-bias in dispersal rate and distance (Linnell et al. 1998). Wang & Schreiber (2001) studied population genetic structure of roe deer at a bio-geographical scale (up to 1000 km between two populations) and suggested that dispersal was male-biased. However, at such a scale processes other than dispersal, such as colonization and population dynamics, also determine genetic structure. Hence, until now, there has been insufficient information available with which to assess sex-specific patterns of roe deer dispersal at a population scale.

Here, we use genetic analysis of a large set of individuals sampled at a local scale to test Greenwood's hypothesis that mating strategy is a primary selective force driving the evolution of dispersal in ungulates. As roe deer exhibit a resource-defence strategy, following Greenwood, we predicted that dispersal should be female-biased. Hence, our null hypothesis was the absence of any sex-bias in roe deer dispersal and our alternative hypothesis was the presence of a female-bias.

2. Material and methods

(a) Study site

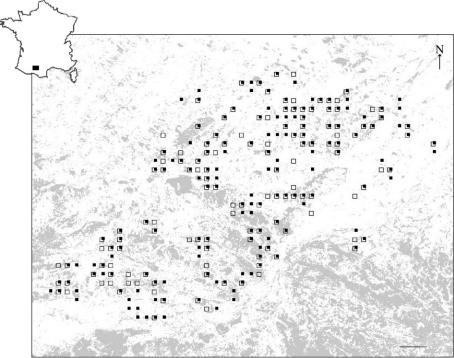
Roe deer were sampled over a 55×40 km² area, in south-western France (figure 1). The landscape is highly fragmented, with a few large forests, numerous small interspersed woodland patches which represent 25% of the surface area, fields and grasslands. The topography is undulating, with elevations ranging from 250 to 400 m.

Figure 1.

Geographical location of the study site and sampling of roe deer individuals in south-western France. Woodland habitat is represented by grey shading, male samples by full squares and female samples by open squares (at least one roe deer was genotyped at each location). Scale bar, 3 km.

(b) Sampling

Skin samples were obtained from legal hunting during the winters 2000–2001 and 2001–2002, and from deer that we caught with long nets in order to fit radio collars for studying space use. For each of the 252 females and 262 males, we assigned a geographical coordinate corresponding to the centre of the square kilometre of the Lambert grid where it was killed or caught. These coordinates can be considered a good estimate of the location of the individual's home range as ranges are generally less than 100 ha in our study site (Cargnelutti et al. 2002) and, during flight, roe deer circle within or near their home range (B. Cargnelutti, personal observation). All of the animals sampled originated from a single continuous population governed by isolation-by-distance (Coulon et al. 2004).

(c) DNA conservation and genotyping

Skin samples were stored in 95% ethanol prior to DNA extraction, which was carried out using the DNeasy Tissue Kit (Quiagen). DNA was amplified using the polymerase chain reaction and genotyped with a multiplex panel of 12 microsatellites (Galan et al. 2003) in a genotyper ABI PRISM 310 Genetic Analyser (Applied Biosystems). Genotypes were determined using Genescan and Genotyper softwares (Applied Biosystems).

(d) Geographic distances

Coulon et al. (2004) showed that the straight-line distance between individual roe deer is less informative and biologically less meaningful for describing gene flow in this population than a distance weighted by landscape connectivity, as measured by woodland presence and structure. For analyses involving inter-individual geographical distances, we therefore decided to use this connectivity-weighted geographical distance. This can be defined as the least-cost path between two individuals, which is a compromise between the straightest line possible and the line following wooded landscape corridors. This distance was calculated in ArcView v. 3.2a, according to Coulon et al. (2004).

(e) Tests of sex-biased dispersal

In order to look for a sex bias in dispersal, we compared inter-individual genetic criteria between the male and female sub-samples to determine the relative level of gene flow within each sex.

Each of the tests we performed involved inter-individual genetic distances. For all possible pairs of individuals of a given sex we calculated:

1. pairwise genetic differentiation a_r following Rousset (2000), generated in Genepop v. 3.3 (Raymond & Rousset 1995); high values of a_r indicate greater dissimilarity between two genotypes;

2. pairwise relatedness r_w following Wang (2002), generated in Mark software (Ritland & Travis 2004); we selected this measure after comparing the performance of several measures of relatedness (from Queller & Goodnight 1989; Ritland 1996; Lynch & Ritland 1999; and Wang 2002) in Mark. We chose the measure that gave the best estimation of relatedness of simulated values, based on their estimated mean and variance (see Ritland & Travis 2004). High values of r_w indicate high similarity between two genotypes. In an outbred population, r_w=0.5 for parents and offspring, 0.5 for full-sibs, and 0.125 for half-sibs (Wang 2002).

(i) Comparison of pairwise genetic distances

We first compared mean inter-individual genetic distances of males and of females at two geographic scales: at a local scale, i.e. for distances of less than 1 km, because the maximum home range size for roe deer in this landscape is 200 ha (Cargnelutti et al. 2002), which corresponds to a circle of 800 m radius; and at a regional scale, i.e. for the whole sample. At the local scale, we expect mean pairwise genetic differentiation to be higher between individuals of the more dispersing sex (MDS) than between those of the more philopatric sex (MPS), because individuals of the MDS, by definition, are less likely to remain in the vicinity of their relatives. In contrast, at the regional scale, average pairwise genetic differentiation between individuals of the MDS should be lower than between individuals of the MPS because higher gene flow within the MDS leads to a homogenization of genotypes at this scale. According to our alternative hypothesis, we thus predicted higher mean genetic differentiation a_r between females than between males at the local scale, and the opposite at the regional scale. With the same reasoning, for our measure of relatedness, we predicted lower mean relatedness r_w between females than between males at the local scale, and the opposite at the regional scale.

In order to verify that any significant difference in genetic distance was not due to a sampling bias (i.e. differences in the spatial distribution of male and female samples), we also compared pairwise connectivity-weighted geographic distances among males and among females.

(ii) Comparison of isolation-by-distance patterns

As a complementary approach, we also adapted a method first employed on bullfrog populations by Austin et al. (2003) to our individual-based sampling scheme. This method considers the relative influence of gene flow and genetic drift on the isolation-by-distance (IBD) pattern. The correlation between genetic differentiation and geographic distance is expected to increase in a monotonic way under IBD; furthermore, as described in Hutchinson & Templeton (1999), the fit to a linear regression of the genetic versus geographic distances should be determined by the relative influence of the two evolutionary forces acting antagonistically: drift leads to local genetic differentiation whereas gene flow homogenizes genetic diversities (Frankham et al. 2002). Hence, drift introduces ‘noise’ into the relationship between genetic and geographic distances as determined by gene flow. As a result, the fit to the IBD pattern is expected to be lower (higher residuals) when the relative influence of drift over gene flow becomes greater, because drift increases the variability of genetic distances for a given geographical distance. Austin et al. (2003) adapted this theoretical framework in order to detect sex-biased dispersal: in the MDS, gene flow is higher than in the MPS. Consequently, the residuals of the regression of genetic distance versus geographic distance are expected to be greater for the latter. From our alternative hypothesis, we therefore predicted higher residuals from the regression of genetic distance versus geographic distance for males compared to females. We performed the regression of inter-individual genetic distances (a_r estimator) on connectivity-weighted geographic distances for males and females separately and calculated the mean of the absolute values for the residuals of the two regressions in R v. 1.7.1 (Ihaka & Gentleman 1996).

(iii) Comparison of geographical distance of related individuals

Finally, we compared the mean connectivity-weighted geographical distances of related individuals, which should be higher for the MDS. We thus predicted higher mean geographic distances between related females than between related males. We arbitrarily defined related individuals as pairs of individuals whose r_w was greater than 0.25 (a relatedness value intermediate between that of full-sibs and of half-sibs chosen in relation to the data distribution).

(f) Statistical procedure

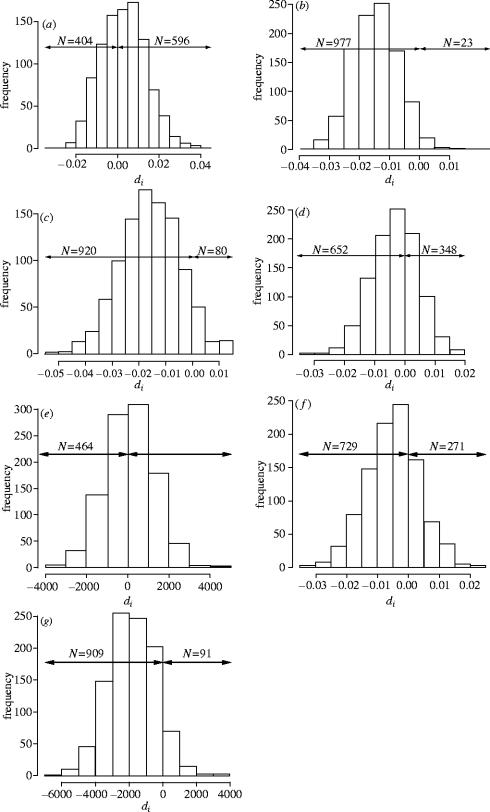
The nature of our data means that each individual occurs N−1 times (N=sample size) in the pairwise distance or residual half-matrices, triggering a problem of non-independence of data which invalidates the simple comparison of male and female values (Prugnolle & De Meeus 2002). Thus, for each test, we carried out 1000 random resamplings without replacement of the relevant half-matrices such that each individual occurred only once in a given resampled set. We then calculated the mean values for males and for females for each of the 1000 resampling sets and derived the difference d_i between the means of the two sexes (d_i=ith resampling mean value of one sex – ith resampling mean value of the other sex), where i is the number of the resampling set. For clarity, for each test, we decided to perform this calculation in the direction that was predicted by our hypothesis, i.e. subtracting the value which was expected to be lower from the one expected to be higher (see figure 2). For the comparison of geographical distances for the whole sample, we did not have a priori an idea of the direction of the bias; we therefore arbitrarily decided to calculate d_i as the resampling mean value for males minus that for females. For all of these tests, under the null hypothesis (i.e. no sex-bias in dispersal), no difference between the sexes is expected and d_i should follow a normal distribution centred on 0; under the alternative hypothesis (i.e. female-biased dispersal), d_i should be significantly greater than 0. We considered the difference to be significant at the 5% level when more than 95% of the d_i values were greater than 0. p-values were calculated as the number of negative d_i, divided by 1000.

Figure 2.

Distribution of d_i for each test. d_i values are expected to be significantly greater than zero under the female-biased dispersal hypothesis. For each graph, the number of d_i values greater and lower than zero are indicated (N). (a) Genetic differentiation a_r at the local scale, $d_i={\overline{a}}_{\text{r}}{(f)}_i-{\overline{a}}_{\text{r}}{(m)}_i$; (b) genetic relatedness r_w at the local scale, $d_i={\overline{r}}_{\text{w}}{(m)}_i-{\overline{r}}_{\text{w}}{(f)}_i$; (c) genetic differentiation a_r at the regional scale, $d_i={\overline{a}}_{\text{r}}{(m)}_i-{\overline{a}}_{\text{r}}{(f)}_i$; (d) genetic relatedness r_w at the regional scale, $d_i={\overline{r}}_{\text{w}}{(f)}_i-{\overline{r}}_{\text{w}}{(m)}_i$; (e) geographic distances, $d_i=\overline{g}{(m)}_i-\overline{g}{(f)}_i$; (f) absolute residuals of the regression genetic distance/ln(geographic distance), $d_i=\overline{s}{(m)}_i-\overline{s}{(f)}_i$; (g) geographic distances of related individuals, $d_i=\overline{g}\text{rel}{(f)}_i-\overline{g}\text{rel}{(m)}_i$. ${\overline{a}}_{\text{r}}{(m)}_i$ and ${\overline{a}}_{\text{r}}{(f)}_i$ are the mean genetic differentiations a_r for males and females, respectively, for the ith resampling set; ${\overline{r}}_{\text{w}}{(m)}_i$ and ${\overline{r}}_{\text{w}}{(f)}_i$ are the mean genetic relatedness r_w for males and females respectively, for the ith resampling set; $\overline{g}{(m)}_i$ and $\overline{g}{(f)}_i$ are the mean geographic distances for males and females respectively, for the ith resampling set; $\overline{s}{(m)}_i$ and $\overline{s}{(f)}_i$ are the mean absolute values of the residuals from the regression of genetic differentiation on ln(geographic distance) for males and females respectively, for the ith resampling set; $\overline{g}\text{rel}{(m)}_i$ and $\overline{g}\text{rel}{(f)}_i$ are the mean geographic distances of related individuals for males and females, respectively.

3. Results

(a) Comparison of pairwise genetic distances

None of the tests we performed, at both local and regional spatial scales, supported our predictions.

Local scale: a total of 152 male–male pairs and 226 female–female pairs were separated by less than 1 km, and so were considered to represent the local spatial scale. Pairwise genetic differentiation at this local scale was higher among males than among females (table 1). Of the 1000 resamplings, d_i was less than 0 in 404 cases (figure 2a), and hence we cannot reject the null hypothesis (p=0.404). Local pairwise relatedness was lower among males than among females (table 1), with 977 values of d_i less than 0. Thus, the prediction of female-biased dispersal leading to lower female relatedness is not supported (p=0.977); rather, this suggests that the opposite may be true (figure 2b).

Table 1.

Raw values of mean pairwise genetic differentiation (a_r; Rousset 2000) and mean pairwise relatedness (r_w; Wang 2002) for pairs of individuals separated by less than 1 km (local scale), and for the whole sample (regional scale). (Standard deviations are given in brackets. N is the number of pairwise distances involved.)

	local scale		regional scale
	ar	rw	ar	rw
males	−0.0003 (0.118)	0.0499 (0.0732)	0.0120 (0.115)	0.0499 (0.0716)
	N=152	N=152	N=34 191	N=34 191
females	−0.0124 (0.139)	0.0714 (0.0869)	0.0280 (0.12)	0.0468 (0.0705)
	N=226	N=226	N=31 626	N=31 626

Regional scale: at the regional scale, the patterns were opposite to those observed at the local scale such that pairwise genetic differentiation was lower among males, and pairwise relatedness was higher among males (table 1). Thus, for both tests, we cannot reject the null hypothesis of no sex-biased dispersal (p=0.920 and p=0.652, respectively; figure 2c,d, respectively). Notice that in fact for both tests the majority of the d_i values were negative, indicating a trend for male-biased dispersal.

There was no sampling bias between the sexes as inter-individual geographic distances were not significantly different among males and among females (mean geographic distance for males=18 544 m, s.d.=10 871 m, mean geographic distance for females=18 422 m, s.d.=10 784 m, p=0.464; figure 2e).

(b) Comparison of isolation-by-distance patterns

The mean absolute value of the residuals from the regression of pairwise genetic differentiation (a_r) on pairwise geographic distance was higher for females (0.0967, s.d.=0.072) than for males (0.0913, s.d.=0.069), contrary to our prediction. Of 1000 resamplings, 729 d_i values were lower than 0, hence we cannot reject the null hypothesis (i.e. p=0.729; figure 2f). Once again, this test in fact suggests a trend for an opposite bias. That is to say, the fact that the residuals were higher for females compared to males indicates that drift is higher and gene flow lower among the female population relative to the male population (see Coulon et al. (2004) for a presentation of the IBD regressions).

(c) Comparison of geographical distance between related individuals

Contrary to our prediction, mean inter-individual geographic distance between related males was slightly higher (18 621 m, s.d.=10 947 m, N=146 pairs) than between related females (18 174 m, s.d.=10 812 m, N=145 pairs). Out of 1000 resamplings, values of d_i were lower than 0 in the vast majority of cases (figure 2g), suggesting a possible tendency for male-biased dispersal.

4. Discussion

In this study, none of the comparisons of the different inter-individual genetic criteria between males and females indicated that we should reject the null hypothesis in favour of an alternative hypothesis of female-biased dispersal in this roe deer population. Furthermore, the raw data and the distributions from the resampling tests taken together in fact suggested, opposite to our predictions, the possibility of a male-biased pattern of dispersal. Hence, from these results, we conclude that dispersal is not female-biased in this population; on the contrary, dispersal may be weakly male-biased in this species. However, further studies are required to investigate this pattern.

Roe deer dispersal has previously been studied, mainly in France and northern Europe, using re-sightings of animals fitted with individually recognizable collars and radio-tracking data (for a review, see Linnell et al. 1998). However, because of small sample sizes and the difficulty of obtaining accurate observation data on this woodland species, it is hard to compare the results of these studies with ours. This highlights the difficulties of studying dispersal from direct data and emphasizes the usefulness of genetic-based analyses. Indeed, studies which exploit the comparison of bi-parentally inherited molecular markers with maternally and paternally inherited ones (e.g. microsatellites, mitochondrial DNA and Y-linked loci, respectively) may provide the best way to determine whether the pattern of slightly male-biased dispersal that we observed is an ecological generality for roe deer (see, for example, Escorza-Treviño & Dizon 2000; Petit et al. 2002; Rosa et al. 2005).

(a) Roe deer as an exception to Greenwood's hypothesis

From Greenwood's (1980) resource selection hypothesis, we predicted a female-biased dispersal for roe deer, a species where males defend resources rather than mates. This hypothesis was not supported by our study; hence we conclude that male mating strategy is not the primary selective force driving the evolution of dispersal in roe deer. Below we discuss possible alternative evolutionary scenarii.

Some authors have cited inbreeding avoidance as an evolutionary force underlying dispersal patterns (e.g. Pusey 1987; Gandon 1999; Perrin & Mazalov 1999; Perrin & Goudet 2001; but see Moore & Ali 1984). As dispersal events may be costly (in terms of energy expenditure and mortality risks), and dispersal of one sex is sufficient to avoid inbreeding, this evolutionary force may lead to sex-biased dispersal. When costs of inbreeding are the same for both sexes, the direction of the bias cannot be predicted, as it is defined either randomly or in relation to phylogenetic constraints (Perrin & Mazalov 2000; Perrin & Goudet 2001). When costs of inbreeding are more important for a given sex, dispersal should be biased toward that sex. This has been suggested to occur in polygynous species, where a successful inbred mating for a male does not preclude other mating opportunities, unlike females (who are fertilized by only one male). In this situation, the cost of inbreeding is predicted to be more important for females and hence they should disperse more than males (Greenwood 1980). Because in roe deer, a weakly polygynous species, inbreeding avoidance should lead to a female-biased dispersal, it seems that this is not the primary force driving the evolution of dispersal. However, inbreeding avoidance could act in synergy with other factors, such as those described below.

Mate choice—associated with inbreeding avoidance—is another potential evolutionary force acting on both natal and breeding dispersal. First, Perrin & Goudet (2001) proposed that choosiness, in polygynous species, should act as an evolutionary pressure toward male-biased natal dispersal: females should choose unrelated males (in order to avoid inbreeding), and thus males should disperse in order to be unfamiliar to females located on their territories. Second, some recent studies have suggested that some adult female roe deer may undergo a kind of breeding dispersal, leaving their home range during the mating period, making brief excursions to a new and distinct area for a few days before returning (Liberg et al. 1998). Such breeding dispersal, if associated with mating events, could also lead to the data pattern we observed. This is because the geographic distance between the females involved in a reproductive event (mother–daughter) remains unchanged, whereas that between the males (father–son) is, on average, artificially increased, compared to a situation where offspring are conceived on the usual mother's home range. Hence, both natal dispersal of males or breeding dispersal of adult females could be responsible for the slight sex-bias we observed in our data set. However, we are unable to distinguish between these two possibilities with the data currently available. Future work should aim to establish the generality of female excursions in roe deer and to determine whether mating occurs during these excursions, for example through direct tracking during the rut coupled with paternity assignment.

A further possible ultimate explanation of the patterns of sex-biased dispersal in general, and specifically in roe deer, is competition (Moore & Ali 1984). Competition cannot induce a sex-bias in dispersal unless one sex is more affected by competition than the other (Dobson 1982; Lambin et al. 2001; Perrin & Goudet 2001). In roe deer, this may be the case: competition for mates may be more important among males than among females (polygyny), whereas competition for resources may be similar between sexes as roe deer exhibit low sexual dimorphism and similar feeding behaviour (Cransac et al. 2001). Because of this asymmetry, dispersal may be density dependent, following the pattern proposed by Wahlström & Liberg (1995) and illustrated in figure 3. These authors suggested a male-biased dispersal at low densities, when females should be philopatric as food is abundant (and costs of dispersal are likely to exceed benefits), while male juveniles may be forced to disperse. This is because abundant resources allow high juvenile growth and development, hence these well-developed male yearlings are viewed as potential competitors and are expelled by adult males (Wahlström 1994). At intermediate density, the model predicts high dispersal rates for both sexes, because females begin to disperse in response to increasing food limitation. At high densities, low dispersal is expected for both sexes because food becomes too limited for yearlings to reach the critical weight threshold necessary for them to be able to cope with dispersal costs. The existence of such a threshold has been suggested in several studies of roe deer (see Linnell et al. 1998). Perrin & Mazalov (2000) suggest that the effective selective pressure acting on the sex-bias in dispersal may depend primarily on the balance between competition for resources and competition for mates. These authors developed a game theory based mathematical model of kin-selection to investigate the consequences of local competition and inbreeding depression on dispersal evolution, which generated similar predictions to Wahlström & Liberg's (1995) hypothesis.

Figure 3.

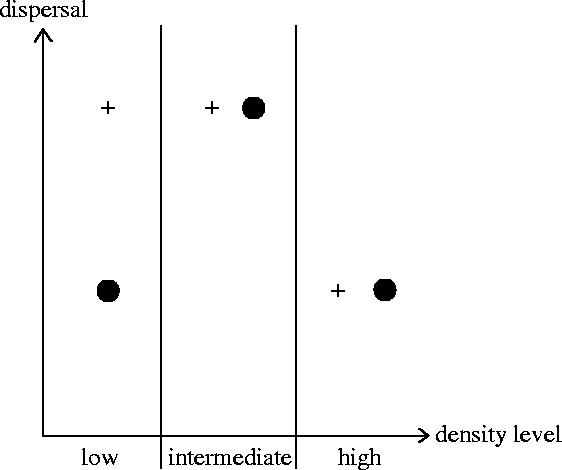
Conceptual model to describe density-dependent sex-specific dispersal in roe deer, after Wahlström & Liberg (1995): male (crosses) and female (circles) dispersal for three levels of density. At low densities, dispersal should be male-biased, while at intermediate to high densities there should be no sex difference (see text for a detailed explanation).

In our study site, we do not have precise information on the density level across the 55×40 km² landscape, but the roe deer population colonized the area in the 1960s and was maintained at rather low density until the 1990s. Population increase is currently limited through hunting. From body weight and vegetation browsing data (N. Morellet and M. H. Hewison, unpublished data), it seems unlikely that the habitat is saturated. A slightly male-biased dispersal in this population, suggested by genetic criteria, which reflect patterns of gene flow over the recent past, may thus be in accordance with Wahlström's hypothesis.

5. Conclusion

This study suggests that dispersal is not female-biased and could possibly be slightly male-biased in this roe deer population. Contrary to Greenwood's hypothesis, it seems possible that dispersal in roe deer could have evolved in response to female mate choice, or male competition for mates and female competition for resources, but this requires further study. Better data on the possibility of breeding dispersal among adult females in particular is especially important for understanding the evolution of dispersal patterns in roe deer. This study also emphasises the need for further investigations of dispersal of mammals with contrasting mating systems across different levels of density in order to identify the potential underlying evolutionary pressures acting on this life history trait. In particular, studies based on extensive genetic sampling of individuals post-dispersal could allow assignment of offspring to parents, thus providing direct estimates of distances and rates of dispersal.