The evolution of parasite manipulation of host dispersal

Abstract

We investigate the evolution of manipulation of host dispersal behaviour by parasites using spatially explicit individual-based simulations. We find that when dispersal is local, parasites always gain from increasing their hosts' dispersal rate, although the evolutionary outcome is determined by the costs-to-benefits ratio. However, when dispersal can be non-local, we show that parasites investing in an intermediate dispersal distance of their hosts are favoured even when the manipulation is not costly, due to the intrinsic spatial dynamics of the host–parasite interaction. Our analysis highlights the crucial importance of ecological spatial dynamics in evolutionary processes and reveals the theoretical possibility that parasites could manipulate their hosts' dispersal.

1. Introduction

Dispersal is an important factor affecting the evolutionary ecology of host–parasite interactions. In particular, host and parasite dispersal can have important consequences for the evolution of parasite virulence (Boots & Sasaki 1999) and local adaptation (Gandon et al. 1996). However, most studies have taken the host perspective by looking for evidence of host dispersal as a strategy to avoid infection. For instance, it has been suggested that hosts might choose to leave infected areas and settle in parasite-free habitats. In several colonial bird species, such as the cliff swallow (Hirundo pyrrhonota), ectoparasites have been shown to be a potential cause for colony abandonment (Loye & Carroll 1991).

On the other hand, there is evidence that parasite transmission and dispersal are intricately linked, and it is widely acknowledged that parasites may benefit from investing in dispersal strategies (e.g. Thrall & Burdon 1999). Empirical and theoretical studies have largely focused on the consequences of parasite propagule dispersal. However, parasites could also take advantage of their hosts' dispersal. For instance, Pérez-Tris & Bensch (2005) have shown that avian malarial parasites that can infect wintering birds and spread to distant areas have a higher local transmission than parasites that are infectious only during summer.

Our aim is to investigate theoretically the intriguing possibility that parasites could actually manipulate host dispersal behaviour to increase their own dispersal and/or transmission (Boulinier et al. 2001). The literature provides numerous examples of parasites that are able to alter their hosts' behaviour (see Moore 2002; Thomas et al. 2005 for recent reviews). Some behavioural alterations are a mere side effect of parasitic infection (Poulin 1995), but others are an adaptation that increases the probability of transmission (Combes 1991). In vertebrates, manipulative parasites can alter the social behaviour of their host through apoptosis, central nervous system inflammation and perturbation of biochemical communication (Klein 2003). Poulin (1994) reviewed 114 studies pertaining to the relation of host behaviour to parasitic infection, and found that parasites had a moderate, but significant impact on host activity and habitat choice. A recently documented example is that of the manipulation of a terrestrial grasshopper by a parasitic hairworm that causes infected insects to be more likely to jump into water, where the adult parasite reproduces (Thomas et al. 2002). In this particular example, a proteomics study showed differential expression of the proteomes of both host and parasite during manipulation (Biron et al. 2005) in agreement with the hypothesis that this host behavioural alteration is not a mere side effect of infection. Such examples suggest that the possibility that manipulative parasites could modify their hosts' dispersal behaviour should not be ruled out.

To explore how such a manipulation strategy can evolve, we formulate a spatially explicit epidemiological model in which parasites can modify the dispersal of their hosts. Although the known examples of manipulation of host behaviour are often quite spectacular and involve complex life cycles, we choose, for the sake of simplicity, to limit our analysis to a single-host parasite with a quite unsophisticated manipulation strategy.

Using stochastic simulations, we determine the conditions of invasion of a rare mutant parasite into a population of hosts infected by a resident parasite strain that has a different manipulative strategy, and apply adaptive dynamics (Metz et al. 1996; Geritz et al. 1998) to determine the evolutionary outcome. The results of our model indicate that there is scope for manipulation of host dispersal. Manipulators will be favoured by selection because the increased dispersal of their hosts allows them to infect more susceptible hosts than non-manipulative parasitic strains. The outcome of selection will depend on the cost of manipulation, the spatial self-structuring of the population and the scale of dispersal. Details such as the lattice structure also have a quantitative effect. We demonstrate that, when dispersal can be non-local, selection on the manipulation of host dispersal can lead to an evolutionarily stable strategy (ESS) even in the absence of cost of manipulation, due to the eco-evolutionary feedback loop between the spatial correlations that arise in the environment and the selective pressures that affect the trait (dispersal) that shapes the spatial structuring of the population. We interpret this result in terms of a trade-off between local exploitation of a cluster of hosts and transmission to other clusters.

We first present the assumptions of the model (§2) and its ecological dynamics (§3). Section 4 then discusses the notion of invasion fitness in the model. In §5, we study the evolution of manipulation of host dispersal rate when dispersal is purely local. In §6, we relax the latter hypothesis and allow the parasite to manipulate its host's dispersal distance.

2. A spatial epidemiological model

Consider a population of hosts that are individually either susceptible (S) or infected by parasites (I). Individuals live on a lattice with periodic boundary conditions, where they interact with at most n nearest neighbours. Each site can be in one of three states: ‘S’, ‘I’ or ‘o’ (empty). We first assume that all demographic processes are local (table 1). Susceptible and infected hosts can reproduce at rates b_S and b_I, respectively, to an empty neighbouring site (reproduction is therefore density-dependent). There is no vertical transmission of the parasite, so that all offspring are born susceptible. Background mortality rates for both host states are equal (d_S=d_I). At the level of the individual, virulence of the parasite is represented as a reduction in the host reproductive effort (‘castration’: b_I<b_S). An infected host can transmit the parasite to a neighbouring susceptible host at rate β_I.

Table 1.

Symbols and description of the model when migration is only local.

type	symbol	description	default value	event and event rate
space	n	number of nearest neighbours	4
	ϕ	probability of drawing a neighbour at random	1/4
demography	bS	birth rate of susceptible host	4
	bI	birth rate of infected host	2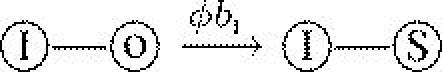
	βI	infection rate	10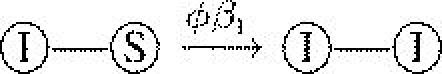
	dx	death rate of type x (S or I)	1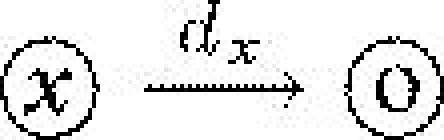
	mI	migration rate of infected host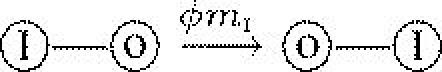
	μ	mutation rate	0.005
	γ	cost of manipulation	0.05
	σ	mutation step	1
variables	px	global density of type x
	qx/y	local density of type x as seen by type y

Parasites are further assumed to be ‘manipulators’, in the sense that they can induce the movement of their host to a neighbouring empty site at rate m_I, whereas susceptible hosts migrate at rate m_S. We suppose that this manipulation is costly, affecting the transmission rate of the parasite. The cost function is assumed to be linear, with ${\beta }_{\text{I}}={\beta }_{\text{I}}^0-\gamma m_{\text{I}}$. Note that our notion of migration differs from that of ‘natal dispersal’, and is more relevant to animal hosts (but see Thrall & Burdon 1999 for studies of seed and spore dispersal in parasitized plants).

To investigate the behaviour of the system when migration is allowed to evolve, we perform individual-based stochastic simulations of the model on a square regular lattice (each individual has at most four nearest neighbours) (Durrett & Levin 1994a). Evolutionary outcomes are studied either by using extensive invasion analysis for several pairs of resident and mutant traits, or by letting the migration rate evolve at a low mutation rate. In the latter case, we start by randomly distributing on the lattice a low density of hosts infected either by a non-manipulative, or by a manipulative parasite. We allow for the migration trait to mutate at rate μ with mutation step σ (e.g. when mutation occurs, host migration rate becomes m_I+σ or m_I−σ (if m_I≥σ) with equal probability). Note that we envision the mutation process resulting from the takeover of the host by a mutant parasite via within-host competition between parasite strains. It is also plausible that mutation occurs during transmission, but this difference should not affect our results as long as the mutation rate is low.

The dynamics of such a spatial ecology can be represented by an infinite hierarchy of spatial moments involving single individuals, pairs of individuals, triplets of individuals, and so on (Rand 1999). The mean-field approach makes the crude approximation that all moments can be approximated using the first moments only (global densities), and therefore ignores the spatial structure (Durrett & Levin 1994b; Wilson 1998). More insight can be gained by taking one further step and keeping track of the local environment of individuals. Correlation equations (or pair approximation; Matsuda et al. 1992; Rand 1999; van Baalen 2000; see Bolker & Pacala 1997 for a similar approach in continuous space) allow us to derive the following exact equations for the expected dynamics of the global densities.

$$\frac{\text{d}{p}_{\text{S}}}{\text{d}t}=b_{\text{S}}{q}_{\text{o}/\text{S}}{p}_{\text{S}}+b_{\text{I}}{q}_{\text{o}/\text{I}}{p}_{\text{I}}-d_{\text{S}}{p}_{\text{S}}-{\beta }_{\text{I}}{q}_{\text{I}/\text{S}}{p}_{\text{S}},$$ 2.1

$$\frac{\text{d}{p}_{\text{I}}}{\text{d}t}={\beta }_{\text{I}}{q}_{\text{S}/\text{I}}{p}_{\text{I}}-d_{\text{I}}{p}_{\text{I}},$$ 2.2

where p_x is the (global) density of type x and q_x/y is the local density of type x as seen by type y (i.e. the probability that a site in the state x is a neighbour of a site in the state y). Note that migration rates do not appear per se in these equations, because migration events leave the number of individuals unchanged, but that the influence of dispersal is incorporated into population dynamics through the local densities. This correlation equations model has been studied in the sessile case where migration rates are zero by Sato et al. (1994) and Boots & Sasaki (2001). If both susceptible and infected hosts move very fast (m_S and m_I are very large), the spatial structure of the system is lost and the model reduces to the classical well-mixed Susceptible–Infective–Removed system (Anderson & May 1979; May & Anderson 1983). In contrast with the mean-field model, the sessile model predicts that the parasite can drive its host to extinction when its transmission rate is larger than a threshold (Boots & Sasaki 2001).

Before investigating the evolution of host dispersal manipulation, we present in §3 the ecological dynamics of the model.

3. Ecological dynamics

Few studies have focused on the consequences of the dispersal of infected hosts for the spatial dynamics of a host–parasite interaction. To explore these effects, we first analyse the host–parasite system for different values of the dispersal rate m_I, no migration of susceptible hosts (m_S=0) and no cost of dispersal (γ=0). We restrict ourselves to the endemic equilibrium of the system, that is we choose parameter values so that the system has a non-trivial equilibrium.

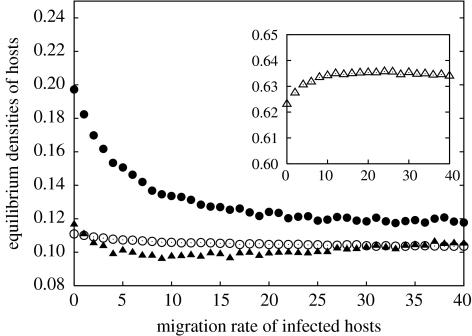
As the reproduction rate of infected hosts has a strong effect on the dynamics, we first investigate the case where infected hosts are sterile (b_I=0). In that case, we observe a decrease in the equilibrium densities of susceptible hosts (figure 1), which saturates when the migration rate becomes very high. Snapshots of the lattice once the attractor state has been reached give some clues: when no dispersal occurs (m_I=0), susceptible hosts form large clusters surrounded by tight clusters of infected hosts (figure 2, top-left panel), but a high migration rate of infected hosts shapes the spatial structuring of the population by producing more diffuse infected clusters and by shrinking the cluster size of susceptible hosts (figure 2, top-right panel). Indeed, in a non-moving population, the centre of a cluster acts as a refuge for uninfected hosts, but if infected hosts can move, they can gain access to the inner part of the clusters. The result is that clusters of susceptible hosts are smaller, and the global equilibrium density of susceptible hosts is reduced. Regarding the global density of infected hosts, equation (2.2) indicates that at equilibrium p_I∝q_I/Sp_S, because q_S/Ip_I=q_I/Sp_S (see Matsuda et al. 1992). When moving infected hosts penetrate a cluster of susceptible hosts, the result will be that the average susceptible host has fewer contacts with other susceptible hosts (local density q_S/S decreases), while contacts with infected hosts increase (local density q_I/S increases). Thus, q_I/S and p_S evolve in opposite directions when m_I increases, resulting in the non-trivial dependency of p_I on migration rate m_I (figure 1, filled triangles). Note however that, with lower values of the transmission rate β_I, increasing the migration rate always leads to an increase in the equilibrium density p_I.

Figure 1.

Equilibrium densities $p_{\text{S}}^{*}$ (dots) and $p_{\text{I}}^{*}$ (triangles) for different dispersal rates of infected hosts. Filled symbols: castrating parasite (b_I=0). Open symbols: non-castrating parasite (b_I=4). Note the difference in scale for the densities of hosts infected by castrating versus non-castrating parasites. Parameters as in table 1.

Figure 2.

Lattice snapshots once the system has settled in its attractor for different values of b_I and m_I. Black and grey squares represent susceptible and infected hosts, respectively.

When the reproduction of infected hosts is unaffected by the parasite (b_I=b_S), the effect of increasing migration rate is much reduced because there is less spatial structure in the population (figure 2, bottom panel). Because offspring of infected hosts are born susceptible, the global density of susceptible hosts is not as sensitive to a change in the migration rate of infected hosts (figure 1, open circles). Therefore, the global density of infected hosts changes as q_I/S when m_I varies, resulting in an increasing saturating trend (figure 1, open triangles).

More generally, the effect of increasing the migration rate of infected hosts is seen to saturate eventually, which is expected as a high migration rate m_I destroys part of the spatial structure.

4. Spatial invasion fitness

We now introduce a second (mutant) parasite strain that differs from the resident strain by having a slightly different manipulation effort, resulting in a slightly different migration rate for the infected host M. Following Metz et al. (1992), we define the fitness of the mutant by its per capita growth rate while rare in the resident population at equilibrium.

The fate of a mutant appearing in a resident population involves three phases (van Baalen 2000). The first phase is dominated by drift and, if extinction does not occur, the neighbourhood structure of the mutant stabilizes at a pseudoequilibrium state (Matsuda et al. 1992). This structure is retained in the second phase where the mutant population expands or contracts. Spatial invasion fitness can be calculated during the second stage. If it is positive, the invasion process enters a third phase where the mutant displaces the resident.

Correlation equations yield the following exact expression for the (spatial) invasion fitness of the mutant (van Baalen & Rand 1998; Boots & Sasaki 1999; Ferrière & Le Galliard 2001; van Baalen 2002):

$$s_{\text{I}}(M)={\beta }_{\text{M}}{q}_{\text{S}/\text{M}}-d_{\text{M}},$$ 4.1

where q_S/M is the local density of susceptible hosts around a host infected by the (rare) mutant parasite, i.e. the expected frequency of a susceptible host in the neighbourhood of a host infected by the mutant parasite. The local density q_S/M depends on the demographic rates and contains information about the spatial structure of the resident population as seen by the mutant during the invasion phase. Actually, s_I(M) is merely the spatial extension of the R₀ argument classically applied in well-mixed populations (Anderson & May 1982; van Baalen 2002).

Since the resident is at equilibrium, we know from equation (2.2) that, when the mutant is rare, $q_{\text{S}/\text{I}}=q_{\text{S}/\text{I}}^{*}=d_{\text{I}}/{\beta }_{\text{I}}$, where $q_{\text{S}/\text{I}}^{*}$ is the average density of susceptible hosts as seen by infected hosts when the system is on its attractor. If both parasites yield the same epidemiological rates β and d, equation (4.1) reduces to $s_{\text{I}}(M)=\beta (q_{\text{S}/\text{M}}-q_{\text{S}/\text{I}}^{*})$, which indicates that a rare mutant parasite will invade if it is surrounded by more susceptible hosts than the resident. Any effect of manipulation of host dispersal will therefore be encompassed in the statistics q_S/M.

5. Evolution of manipulation of host dispersal rate

(a) No cost of manipulation (γ=0)

When there is no cost of manipulation, a manipulative parasite that increases its host's migration rate will always invade and displace a resident population with a lower manipulation effort (results not shown). This situation implies that a parasite can increase its transmission by increasing its host's dispersal, because a moving infected host will encounter more susceptible hosts than a non-moving infected host, since it will be able to access the centre of the clusters of sessile susceptible hosts, thereby enhancing the parasite's transmission. This result is reminiscent of the fact that, in most spatial ecologies, there will be a positive, albeit weak, selective pressure on migration (van Baalen & Rand 1998; Koella 2000). Selection thus favours individuals that ‘diffuse’ faster.

(b) Costly manipulation (γ>0)

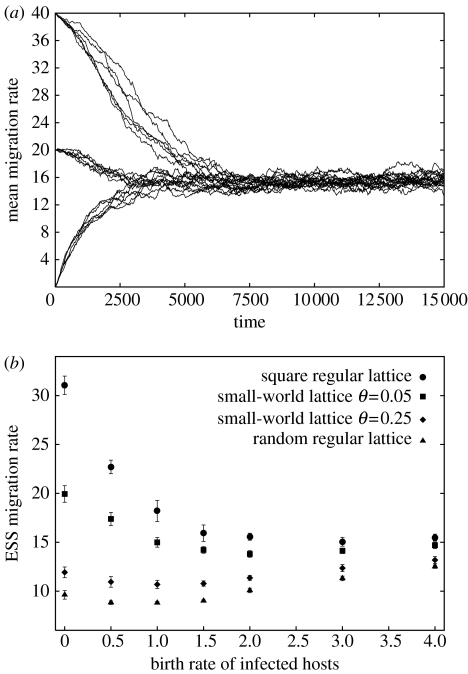
When the cost of manipulation increases with host dispersal, selection drives the system to an evolutionarily stable migration rate, balancing the benefits and the costs of dispersal for the parasite (figure 3a). The results of the model are qualitatively robust, since we find the same qualitative pattern with different levels of castration, virulence-induced mortality and transmission, as well as with non-zero migration rates for susceptible hosts. The use of different cost functions alters only the level of the ESS in a predictable way, with accelerating costs leading to lower ESS migration rates and decelerating costs leading to higher ESS migration rates.

Figure 3.

Evolution of migration rate with γ=0.05. (a) Mean migration rate on a 100×100 lattice with b_I=2. Six runs are shown for each of three initial conditions (m_I=0, 20 or 40). (b) ESS migration rates for different values of b_I, on various lattice structures. The mean and standard deviation of 10 runs are shown. Parameters as in table 1.

(c) Influence of parasite-induced castration

In our simulations, we observe a decreasing saturating trend for the change in ESS migration rate as the fertility of infected hosts increases (figure 3b, circles). Indeed, if the fertility of infected hosts is high, infected hosts tend to be surrounded with more susceptible hosts (their offspring) and fewer empty sites. Hence, when infected hosts reproduce, a high dispersal rate does not allow the parasite to increase its fitness as much as when infected hosts are sterile and surrounded by a high density of empty sites. In other words, the benefits that can be achieved by increasing the host's dispersal rate saturate more quickly when infected hosts can reproduce, leading to a lower ESS migration rate.

(d) The role of lattice structure

Although we assume that the costs of migration are physiologically constrained, we make no assumption regarding the benefits of manipulation, so that these are solely determined by ecological spatial dynamics. We investigated the role of lattice structure, and we found that it has a strong effect on the benefits to be gained from a manipulation of host dispersal. In figure 3b, we plotted the ESS migration rate as a function of parasite-induced castration for different lattice structures: a square regular lattice; a random regular lattice, in which each site is connected to four randomly chosen sites in the lattice, and two small-world lattices, that is, square lattices in which a proportion θ of the connections have been randomized (we chose θ=0.05 and θ=0.25; Watts & Strogatz 1998). As randomness increases, selection on migration rates weakens because random graphs have a smaller characteristic path length, so that an infected individual is much ‘closer’ to a susceptible host on a random network than on a square lattice. Even a small amount of randomization has a great impact on the ESS migration rate. The difference is more striking for small values of the fertility of infected hosts, because high reproduction rates of infected hosts on a square lattice lead to more randomness.

In summary, the model predicts that manipulation of host dispersal rate can increase the parasite local transmission, but that the actual benefit of the strategy is reduced by features that decrease the clustering of susceptible hosts, such as reproduction of infected hosts, randomness in lattice structure, or migration of susceptible hosts.

6. Evolution of manipulation of the scale of host dispersal

In this section, we decouple the scale of dispersal from the scale of reproduction and infection, allowing parasite manipulation of the host to such extent that dispersal events are not restricted to the nearest neighbour sites. We focus on the evolution of manipulative effort when the parasite can alter the dispersal distance of its host rather than the rate of dispersal events. Note that, throughout this section, we assume no cost for manipulation (i.e. γ=0).

(a) Long-range dispersal on a lattice

We perform extensive simulations of the individual-based model to investigate numerically the invasibility conditions of a mutant parasite in a resident population with a different manipulative effort. However, the expression for the invasion fitness given in equation (4.1) is still valid, as are the conclusions of §4.

Dispersal was implemented using a uniform kernel with a cutoff distance D_I (but exponential and gaussian kernels yield qualitatively similar results). In the following, we assume that dispersing individuals move to a randomly chosen site located inside a circle of radius D_I only if that site is empty, but similar results are obtained when individuals can disperse to already-occupied sites. Migration events still occur at rate m_I, so that in this model we can alter both the rate and distance of dispersal.

(b) Selection for intermediate dispersal distance

We first assume that infected hosts do not reproduce (b_I=0), but later examine the consequences of relaxing that assumption.

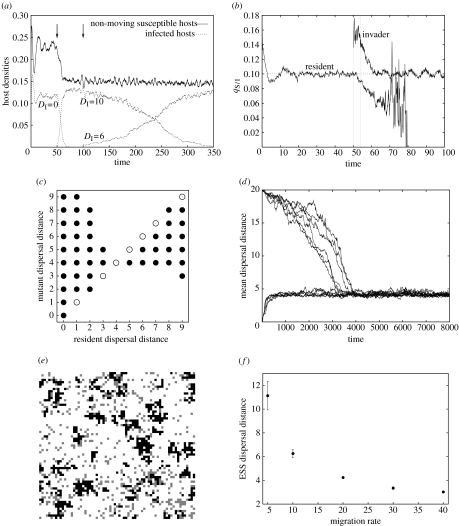
An invasion analysis was performed in the stochastic simulations by waiting for the resident population to reach the attractor state, then introducing a mutant parasite at a low density. Results of a typical run are presented in figure 4a. Stationary infected hosts are seen to be quickly displaced by long-range dispersers; however, these are displaced, albeit at a slower rate, by dispersers with an intermediate dispersal distance. Figure 4b shows the temporal changes in the local density of susceptible hosts as seen by resident (D_I=0) and mutant (D_I=10) parasites. We see that once the resident population (D_I=0) has settled in the attractor state, the local density q_S/I fluctuates around 0.1, which corresponds to the ratio d_I/β_I for our parameter values. When the mutant (D_I=10) is introduced, it quickly reaches a pseudoequilibrium value ${{\displaystyle \tilde{q}}}_{\text{S}/\text{M}}$ that is above the attractor value (average value: 0.153, computed from the interval when the mutant is rare). The mutant parasite can then invade, because the local density of susceptible hosts as seen by the mutant parasite is higher than that of the resident strain. That is, although the mutant parasite is globally rare in the population during the invasion phase (p_M≈0), it experiences a higher density of susceptible hosts than the resident (q_S/M>q_S/I). Once the mutant has displaced the resident, q_S/M stabilizes around the equilibrium value 0.1. When the global density of resident parasites p_I is very low, we observe large fluctuations of q_S/I as expected.

Figure 4.

Manipulation of host dispersal distance. (a) Invasion analysis of the stochastic model. The introduction of mutant parasites into the population is indicated by arrows. (b) Local densities of susceptible hosts as seen by resident and mutant parasites. The local densities are computed from the run shown in (a), but we only present the first invasion (t<100). The vertical dashed lines delimit the interval where the mutant is rare. (c) Numerical pairwise invasibility plot. Filled circles indicate that the mutant has invaded after 300 time units. Open circles were added to complete the diagram when the resident and the mutant are the same. (d) Evolution of the mean migration distance on a 100×100 lattice. Six stochastic realizations are shown for each of two initial conditions (D_I=0 or 20). (e) Snapshot of part of the lattice on its attractor, for D_I=5. (f) ESS dispersal distance for different values of migration rate m_I. The mean and standard deviation are calculated from a sample of 10 runs. Lattice size: 100×100. Unless otherwise specified, all parameters are as in table 1, lattice size is 300×300, m_I=20, b_I=0, γ=0.

Extensive invasion tests, summarized in a numerical pairwise invasibility plot (figure 4c), and results of simulations where small mutations of the dispersal rate can occur at a low rate (figure 4d), confirm that the outcome of selection is manipulation for an intermediate ESS dispersal distance.

Interestingly, the existence of an ESS is not a consequence of a physiological cost, but it is the outcome of the interplay of selection pressures and spatial dynamics. Insight into the underlying mechanisms can be gained by observing a typical snapshot of the lattice (figure 4e). When susceptible hosts do not move and infected hosts are sterile and moving, susceptible hosts form small patches while infected hosts are more evenly distributed on the lattice. Infected hosts that disperse at intermediate distances take more advantage of the spatial structure of the susceptible hosts, as they strike the optimal balance between colonization ability and local exploitation of clusters of susceptible hosts. We will outline in §7 the similarities of this trade-off with a transmission–virulence trade-off.

The penalty incurred by far-dispersing infected hosts, however, becomes negligible when the patchy spatial pattern disappears, for instance when infected hosts can reproduce as well, or with long-distance dispersal of susceptible hosts. The evolutionary outcome is then completely different: for moderate to high reproduction rate of infected hosts, selection appears to drive the system to high values of dispersal distance, of the same order as the lattice size. It is thus technically difficult to prove that the system settles into an ESS in the absence of any physiological cost of manipulation, but it seems likely that selection favours parasites that causes their host to move as far as possible.

On the contrary, we found that the birth rate of susceptible hosts has little quantitative and qualitative impact on the existence of an ESS dispersal distance. Although it is not feasible to carry out an exhaustive sweep of all parameter values, these results suggest that the outcome of selection is affected most by demographic traits that shape the spatial correlations between susceptible and infected hosts, such as the birth rate of infected hosts, whereas demographic traits that affect the clustering of susceptible hosts only, like b_S, are less important.

Interestingly, ESS dispersal distance decreases when the migration rate increases, and the decrease saturates at high migration rates (figure 4f). This result supports our hypothesis that the evolution of dispersal distance manipulation is chiefly determined by the optimal exploitation of the local patch of susceptible hosts: as infected hosts become more likely to move, the best strategy for the parasites is to lower the dispersal distance of their hosts, because frequent, small steps around the patch of hosts allows a better exploitation of the cluster. The same rationale explains why, if we keep dispersal distance at a fixed intermediate value (D_I>1), evolution of the migration rate results in an intermediate ESS migration rate (results not shown). Thus, whether or not a mutant parasite can invade depends in a subtle way on the overall pattern of dispersal, as determined by both the rate and scale of migration events.

Note that a similar trend was found for the influence of the transmission rate (results not shown): as the efficiency of local infection increases, the advantage of being harboured in a far-dispersing host decreases.

7. Discussion

We have shown that manipulation of host dispersal behaviour can evolve in a spatially structured population. No specific assumptions were made regarding the benefits that a parasite gains from altering its host's dispersal behaviour, other than modifying the host's contact pattern. The evolutionary outcome in our model is solely determined by the emergent spatial dynamics, which is in turn shaped by the selective pressures that affect the manipulative trait.

If the parasite manipulates its host's migration rate but dispersal is restricted to an individual's nearest neighbours, the outcome of selection is predicted to be an evolutionarily stable rate that is conditioned by the costs-to-benefits ratio. The situation is notably different when dispersal can take place at greater spatial scales. In that case, selection can drive the system to an ESS characterized by an optimal manipulation effort (and thus an intermediate dispersal distance or dispersal rate), even in the absence of a physiological cost of manipulation or dispersal. The lack of an explicit trade-off between manipulation of dispersal and other parasitic traits highlights the crucial role that spatial structure plays in the eco-evolutionary feedback loop.

We interpret our results in terms of the optimal exploitation by the parasite of a cluster of susceptible hosts. If dispersal is not local, an intermediate migration rate, or an intermediate dispersal distance, appears to be the optimal strategy for the parasite, because it strikes a balance between local exploitation of the cluster of susceptible hosts and colonization of other clusters. This can also be seen as an example of a virulence–transmission trade-off (Anderson & May 1982). However, in a spatially structured population, the relevant unit of selection is the cluster of hosts (van Baalen & Rand 1998), so that we should define virulence at that level, as the local exploitation of the cluster of hosts. In this sense, our results provide an example of how a virulence–transmission trade-off can emerge from spatial mechanisms.

Parameters that have a strong effect upon the correlations between susceptible and infected hosts also have a strong impact on our conclusions. The benefits of manipulation of host dispersal will be affected by demographic parameters that reduce the clustering of susceptible hosts, such as local (or non-local) reproduction of infected hosts, non-local transmission of parasites, or dispersal of susceptible hosts. Likewise, lattice structure is a key component of the manipulator's fitness: we show that, as randomness increases, the selective pressure on manipulation of migration rate weakens.

More important is the impact of fertility of infected hosts on the evolution of the manipulation of dispersal distance. When infected hosts reproduce, they become surrounded by susceptible offspring. The direct transmission of the disease to relatives results in a high density of infected hosts. Thus, the patchy structure of the host population is destroyed, and with it the main selective pressure acting against the increase in dispersal distance. Consequently, a low fertility of infected hosts is required for selection to favour intermediate investment in the manipulation of dispersal distance.

In this study, we investigated a simple linear trade-off between transmission rate and migration rate. However, the costs of manipulation can affect the parasite physiology in more than one way: which demographic trait is affected by the cost may be important. We cannot exclude the possibility that costs affecting virulence components such as parasite-induced mortality or castration would not yield different results. If dispersing hosts are more likely to be killed, for instance, manipulation of host dispersal will increase the parasite's virulence. This feature can be expected to have important evolutionary consequences.

We have limited most of our analysis to the case where susceptible hosts do not move, but, as stated above, we expect that such movement will have a significant impact on our results. Moreover, as dispersal is a shared trait on which both the parasite and its host have an influence, it is clear that coevolution patterns are expected when both the host and the parasite can make decisions related to whether to move or not: susceptible hosts can choose to move away from infected hosts, and infected hosts can choose to disperse to protect their susceptible relatives, or to retaliate and resist the manipulation. There is much to be done in trying to understand how the common good and private interests of both partners shape the selective pressures that act on the dispersal behaviour of hosts and parasites (van Baalen & Jansen 2001). This coevolution will be the subject of a separate paper.

Our results re-emphasize the important evolutionary consequences of spatial structure, and stress the fact that the scale at which ecological events take place can have important evolutionary effects. Other studies have also pointed out that evolution of dispersal distance could result in an ESS simply because of intrinsic dynamics. Smith & Wilson (in preparation) show that, in a three-species system (plant, pollinator and parasitoid), selection can lead to large-scale spatial structuring that results in an ESS characterized by metapopulation dynamics on the verge of extinction.

The present analysis is restricted to an endemic host–parasite interaction, but the ecological and evolutionary dynamics of a host–parasite system close to the extinction boundaries of the parasite are currently under investigation. Correlation equation models suggest that the migration rate has only a slight, quantitative effect on these boundaries (S. Lion 2004, unpublished results), but some preliminary results show that a virulent parasite on the edge of extinction can increase its host mortality beyond the critical level if infected hosts disperse non-locally and far enough, possibly as the result of manipulation. This phenomenon is expected, as long-distance dispersal of infected hosts prevents virulent parasites from ‘burning out’ the cluster of hosts they exploit before contacting clusters of susceptible hosts (see Rand et al. (1995) for an explanation of the mechanism for the evolution of the transmission rate). However, this possibility calls our attention to the fact that long-distance dispersal events in host–parasite interactions are certainly of paramount importance in the evolution of virulence (see also Boots & Sasaki 1999).

From a perspective of virulence management, dispersal of infected (and susceptible) hosts appears to be an important, but neglected, factor in the eco-evolutionary dynamics of host–parasite interactions. Furthermore, because increased host mobility tends to disrupt patterns of relatedness, one can expect that host dispersal will favour increased virulence (van Baalen 2002). Our preliminary results indicate that the dispersal of infected hosts may lead to increased parasite-induced mortality, as it allows persistence of highly virulent parasites that would otherwise go extinct. Further studies are needed to explore the complex array of selective pressures that act on dispersal and virulence evolution.

Finally, in spite of the difficulty of measuring dispersal and assessing manipulation of the host in the field, we believe our results call for the development of new experimental methods to study the evolution of dispersal and manipulation behaviour in host–parasite interactions.