Skip to main content
PMC home page
Proceedings of the Royal Society B: Biological Sciences logoLink to Proceedings of the Royal Society B: Biological Sciences
. 2006 Jan 24;273(1591):1253–1260. doi: 10.1098/rspb.2005.3440

Fitness landscapes support the dominance theory of post-zygotic isolation in the mussels Mytilus edulis and M. galloprovincialis

Nicolas Bierne 1,*, François Bonhomme 1, Pierre Boudry 2, Marta Szulkin 1, Patrice David 3
PMCID: PMC1560276  PMID: 16720399

Abstract

We studied the genetic basis of post-zygotic isolation in the marine mussels Mytilus edulis and Mytilus galloprovincialis. Evidence was obtained for a high number of recessive Dobzhansky–Muller substitutions in the genome of these two mussel taxa. We analysed the segregation of unlinked diagnostic markers in the progeny of two backcrosses and an F2 cross, 36 h and 200 days after fertilization. Directional selection favouring M. galloprovincialis genotypes was observed in both kinds of cross. In the F2, epistatic interactions between each pair of chromosome fragments mapped by the markers were identified in addition. Our results imply that homozygous–homozygous interactions are required for breakdown of coadaptation, in accordance with the dominance theory of post-zygotic isolation. Endogenous post-zygotic selection distributed over many loci throughout the genome provides the missing factor explaining the astonishing persistence and strength of barriers to neutral introgression in such a dispersive taxon as Mytilus.

Keywords: hybrid zone, hybrid breakdown, negative epistasis, post-zygotic isolation, Dobzhansky–Muller incompatibilities, Mytilus

1. Introduction

The genetic basis of post-zygotic isolation is of long-standing interest in the study of speciation (Coyne & Orr 1998; Orr & Presgraves 2000; Gavrilets 2004). There is now overwhelming evidence that hybrid fitness depression results from the accumulation of alleles that enhance fitness in their own genetic background but lower fitness in the genetic background of other species. The combination of alleles at two or more loci involved in negative epistatic interactions in hybrid genotypes are known as Dobzhansky–Muller (DM) incompatibilities in recognition of the pioneering work of Dobzhansky (1937) and Muller (1942). The beauty of the DM model is that the accumulation of alleles (namely DM substitutions) involved in DM incompatibilities allows reproductive isolation to evolve without populations having to cross-adaptive valleys (Orr 1995; Orr & Turelli 2001; Gavrilets 2004). Only recently, though, were some attempts made to refine the description of the genetic basis of DM incompatibilities (Turelli & Orr 2000).

The motivation for a more detailed description of DM incompatibilities mainly comes from two standard observations: (i) in species with sex chromosomes, hybridization typically causes problems to the heterogametic sex, i.e. Haldane's rule (Haldane 1922; Laurie 1997) and (ii) hybrid breakdown is less pronounced in F1 than in successive F2 or backcross generations (Dobzhansky 1937; Edmands 1999). Both phenomena could be accounted for by the simple hypothesis that DM substitutions are preponderantly recessive in their effects on hybrid fitness so that they are expressed when hemizygous in the F1 or when homozygous in successive generations (Muller 1940; Turelli & Orr 2000). If this is confirmed, such a result would have important implications for the probability and dynamics of speciation (Gavrilets 2004). The validation of the dominance theory of post-zygotic isolation (sensu Turelli & Orr 1995) requires more direct investigations of the genetic architecture of DM incompatibilities. Although numerous investigations have provided support to the dominance theory in Drosophila (reviewed by Turelli & Orr 2000), few tests have been attempted in other organisms so far. These studies investigated major genes with strong effect (e.g. sterility or inviability), involved in the reproductive isolation of genetically well-delimited species that do not hybridize in nature (Orr & Presgraves 2000). In addition, most of the examples available to date relate to X-linked genes for which the evolution should differ from autosomes (Charlesworth et al. 1987). To further refine our knowledge of DM substitutions and test the universality of the dominance theory, data are needed on randomly found autosomal loci, with moderate effect on fitness and involved in the reproductive isolation of more weakly isolated taxa. Although the hybrid zone literature has long emphasized the importance of epistasis (Barton & Hewitt 1985), the detailed genetic architecture of reproductive isolation has only been investigated in a few cases (Rieseberg & Buerkle 2002).

Here, we have conducted a blindfold search for DM incompatibilities in the mussels Mytilus edulis and Mytilus galloprovincialis. These two mussel taxa form a well-known mosaic hybrid zone along the western European coast (Skibinski et al. 1983; Coustau et al. 1991a; Daguin et al. 2001; Bierne et al. 2003c). Some pre-zygotic isolation mechanisms have been documented in previous studies such as habitat preference (Gosling & McGrath 1990; Bierne et al. 2003b), spawning asynchrony (Gardner & Skibinski 1990; Secor et al. 2001; Bierne et al. 2003b) and assortative fertilization (Bierne et al. 2002a). However, we argued that these mechanisms were insufficient alone to explain the observed strength of the barrier to introgression of neutral markers (Bierne et al. 2002a,b). As some hybrid genotypes are produced in visible numbers, theory would predict that neutral introgression should proceed quickly unless some categories of hybrids exhibit reduced fitness (Barton 2001). Yet, the existence of intrinsic hybrid breakdown still remains controversial in Mytilus (e.g. Wilhelm & Hilbish 1998). Surprisingly, the fitness of hybrids has mostly been investigated using correlations between genotypes at marker loci and phenotypes in natural populations (Gardner 1994b), while experimental crossing has seldom been used (but see Beaumont et al. 1993, 2004) and has never been conducted up to the F2. However, the variable degree of local introgression in natural populations poses the problem that so-called ‘hybrid individuals’ are complex genetic mosaics in which neutral loci may have loose or unknown linkage disequilibrium with potentially selected loci (Bierne et al. 2003c). In contrast, a high proportion of useful and perfectly defined hybrid genotypes can be produced in the lab. We have conducted an analysis of the fitness of genotypes at three unlinked chromosomal regions marked by neutral loci in backcrosses and F2s. Following previous work (reviewed in Bierne et al. 2003a), we by-passed the difficulty of measuring fitness in hatchery experiments by the use of molecular markers and a diachronic sampling scheme. We obtained support for the dominance theory and a high number of recessive DM substitutions in the genome of the two mussel taxa.

2. Material and methods

(a) Crosses, larval rearing, sampling and genotyping

F1 hybrids obtained from a previous experiment (Bierne et al. 2002a), M. edulis from Grand-Fort-Philippe (North Sea, France) and M. galloprovincialis adults from Sète (Mediterranean Sea, France), were individually induced to spawn as previously described (Bierne et al. 2002a). Five female and five male M. galloprovincialis, one F1 female and five F1 males emitted gametes. Unfortunately, M. edulis individuals did not spawn, probably because they were insufficiently mature. Gametes were sieved, counted, pooled according to sex and genotype, and fertilization was performed as in Bierne et al. (2002a) following four kinds of treatment: an F2 cross between the oocytes of the F1 female and the pooled sperm of the five F1 males; two backcrosses on M. galloprovincialis, between oocytes of the F1 female and the pooled sperm of the five M. galloprovincialis males (hereafter BC1) and between pooled oocytes of the five M. galloprovincialis females and the pooled sperm of the five F1 males (hereafter BC2); and finally, a control cross between M. galloprovincialis males and females.

In contrast to the previous F1 generation, larval rearing was not performed in our laboratory in Sète, on the Mediterranean Sea, but in the experimental IFREMER hatchery of La Tremblade (Charente Maritime, France) on the French Atlantic coast, a region where natural populations are predominantly M. edulis (Bierne et al. 2003c). The salinity of the seawater was 27‰. Otherwise, we followed the same protocol as previously described (Bierne et al. 2002a).

Samples were taken 36 h after fertilization and at the juvenile stage, 200 days after fertilization (D200). DNA extraction of individual D-larvae and juveniles was performed according to our standard protocols (Bierne et al. 2003a). Sample sizes were approximately 100 for the F2 cross and approximately 50 for backcrosses. The sampling effort was stronger in the F2 treatment because more genotypes are produced (e.g. nine bi-locus genotypes are produced in the F2, while only four are produced in a backcross). Three length-polymorphic DNA loci were used, Glu-5′ (Rawson et al. 1996), mac-1 (Ohresser et al. 1997) and EFbis (Bierne et al. 2002a), using the primer sequences and the fluorescent dye 5′ end-labelled-primer technique described in Bierne et al. (2003c). Overall we screened 1230 single-locus genotypes. Although several alleles were observed at loci mac-1 and EFbis, they were here used as bi-allelic loci—alleles at a single locus were pooled into species-specific compound alleles according to their frequencies in reference samples from each species (Bierne et al. 2003c). Synthetic alleles characteristic of M. galloprovincialis populations were called ‘G’ and synthetic alleles characteristic of M. edulis populations were called ‘E’. A non-negligible level of introgression is observed in natural populations at these loci (Bierne et al. 2003c); however, they appeared to be diagnostic of the ancestral M. edulis and M. galloprovincialis genomes in the present experiment, i.e. we were lucky enough that parents did not carry introgressed alleles so that M. galloprovincialis parents were tri-homozygotes for G alleles, M. edulis parents were tri-homozygotes for E alleles and F1 parents were tri-heterozygotes. The estimated population frequencies of alleles observed in parents are given in Table S1 in the electronic supplementary material. The segregations we observed at the early larval stage (see §3) allowed us to consider these three loci as unlinked.

(b) Statistical analyses

Population sizes of larval stocks were estimated every 2 days during the 19 days of larval growth for each treatment. This allowed us to estimate exponential larval mortality rates, β, from a loglinear regression according to the following model: N(t)=α Exp(−βt), where N(t) is the stock size at time t.

Mendelian proportions and homogeneity of genotypic frequencies among loci, time samples and crosses were tested using Fisher's exact tests in the Genepop software (Raymond & Rousset 1995). Pairwise associations of alleles across loci have been estimated and tested with the maximum likelihood method of Barton (2000). Multilocus genotype proportions have also been analysed with the help of a simple hybrid index that was the number of G alleles per individual. Significance levels of tests were adjusted for multiple testing according to a sequential Bonferroni procedure (Rice 1989), but probabilities below the 5% threshold (before adjustment) are mentioned.

We drew fitness landscapes. We here define a fitness landscape to be the simple relationship between genotype and fitness and we do not consider landscapes that depict the relationship between some variables of the genetic structure of a population and its mean fitness (a definition for which some authors reserve the term ‘adaptive’ landscape, see Gavrilets 2004). As a surrogate of fitness we used survival rates estimated from the evolution of genotype frequencies between the two time samples, 36 h and 200 days after fertilization. Fitnesses were standardized by the fittest genotype, i.e. the fittest genotype had a fitness of 1. An averaged fitness landscape was obtained by averaging fitness across landscapes and by considering symmetrical genotypes (e.g. EEGG and GGEE) as identical.

(c) A simple model

We investigated the consequences of the observed fitness landscape on the evolution of a hybrid zone using a simple model. Our basic question was whether epistatic interactions were sufficiently strong to prevent introgression and generate a stable hybrid zone. We considered a diploid model with two unlinked loci with two alleles G and E. Fitnesses of the nine genotypes were specified at the beginning of the simulation. We modelled a secondary contact of populations initially fixed for alternative alleles using a classical one-dimensional stepping-stone model (Feldman & Christiansen 1974). Demes on the left side of the chain were fixed for the GGGG genotype and demes on the right side were fixed for the EEEE genotype. The migration rate between demes was m (half in either direction). Migration was followed by reproduction and selection. The model is deterministic—genotypic frequencies in each deme at a given generation are deduced from the frequencies of the previous generation after accounting for migration, recombination and selection (e.g. Slatkin 1975). We registered allele frequencies in order to depict cline shapes and linkage disequilibria that inform us about the strength of the barrier to gene flow. A Borland Delphi v. 4.0 program is available from the authors upon request.

3. Results

(a) Larval mortalities

Exponential larval mortality rates (β) and the proportion of dead larvae after 19 days of larval growth are presented in table 1. The exponential model fitted well with the data and provides a synthetic measure of the dynamics of larval mortality (in other words, we did not observe sudden peaks in mortality rates during the larval stage). Overall we observed high larval mortalities which are common features in hatchery experiments (e.g. Beaumont et al. 1993). Nonetheless, mortality was far more pronounced in the tank where the F2s were grown than in any other tanks. Unfortunately, in the absence of replicates we cannot disentangle an always-possible tank effect. Indeed, between-tanks variance in mortality is frequently high during larval rearing. However, previous experiments in the hatchery of La Tremblade have sometimes managed to eliminate tank effects (Ernande et al. 2003). In the present study, the observed variance in mortality rates was low, with very similar results obtained for every non-F2 treatment (table 1). Maternal effects could also explain the results of the F2 cross. However, a maternal effect is not corroborated by the results obtained with the BC1 cross that share the same F1 female but exhibited a similar mortality rate to other non-F2 treatments. Although the higher mortality of F2 larvae may not be taken at face value, there is no evidence to suggest this was artefactual. Furthermore, this result is in agreement with the fact that differential larval mortalities were observed between time samples in the F2 but not in backcrosses.

Table 1.

Exponential larval mortality rates (β) and proportion of dead larvae after 19 days of larval growth.

tank 1: F2 (♀F1×♂F1) tank 2: BC1 (♀F1×♂G) tank 3: BC2 (♀G×♂F1) tank 4: control (♀G×♂G)
β±95% CI 0.17±0.04 0.06±0.02 0.06±0.03 0.08±0.01
mortality at day 19 93% 67% 70% 75%
Open in a new tab

(b) Genotype frequencies in backcrosses

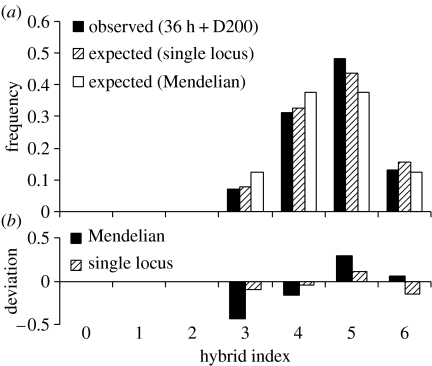
Backcrosses correspond to the case where one type of parent is heterozygous EG and the other type is homozygous GG, at the three loci. Two single-locus genotypes are expected in the progeny, EG and GG, in a 1 : 1 ratio. Numbers of genotypes in each sample are reported in Table S2 in the electronic supplementary material. No significant departure from the Mendelian expectation was observed at the single-locus level within samples. As homogeneity in genotype frequencies was never rejected among samples (after correction for multiple testing but often at the 5% level, Table S2), we were able to pool the results across sampling times, loci and treatments (BC1 and BC2). We found a significant overall tendency for an excess of GG over EG genotypes (55% of GG). This was more pronounced in BC2 (58% of GG) than in BC1 (52% of GG). Note that we always needed to pool time samples to obtain significant deviations while heterogeneities between time samples were never significant. Multilocus genotype frequencies did not depart from those expected under free recombination and association tests were never significant (data not shown). The single-locus trend for an advantage of G alleles was observed at the multilocus level. This is illustrated in figure 1, where the hybrid index distribution is compared to the Mendelian expectation with no linkage. In figure 1, we also have plotted the multilocus expectation deduced from the single-locus frequencies with the assumption of no linkage in order to illustrate the absence of disequilibrium.

Figure 1.

Figure 1

Open in a new tab

(a) Observed tri-locus hybrid index distribution in backcrosses (pooling the two backcrosses, BC1 and BC2, over the two sampling times, 36 h and D200), expected hybrid index distribution from single-locus frequencies with the assumption of no linkage and expected hybrid index distribution from single-locus Mendelian expectations and no linkage. (b) The deviations of the observed distribution from the Mendelian expectation with no linkage and the expectation from single-locus frequencies and no linkage.

(c) Genotype frequencies in the F2s

F2s correspond to the case where both parents are EG heterozygotes. Three single-locus genotypes are expected in the progeny—EE, EG and GG—in a 1 : 2 : 1 ratio. Thirty-six hours after fertilization, single-locus genotype frequencies did not depart significantly from the Mendelian expectation (table 2). Homogeneity in genotype frequencies among loci was not rejected which allowed us to pool results across loci. Genotype frequencies pooled across loci agreed well with the Mendelian expectation (0.94 : 2.13 : 0.94). In addition, association tests were not significant (not shown) suggesting once again that our loci segregated independently.

Table 2.

Genotype numbers, tests of the Mendelian expectation and heterogeneity tests in the F2. (Significant tests at the experimentwise level are in bold. n.s.p>0.05; *0.01<p<0.05; **0.001<p<0.01; ***p<0.001; anot significant at the experimentwise level; —, not feasible.)

Glu-5′ (EE : EG : GG) EFbis (EE : EG : GG) mac-1 (EE : EG : GG) ∑locus
F2-36 h 23 : 41 : 30n.s. 24 : 48 : 22n.s. 19 : 61 : 14*,a 66 : 150 : 66n.s.
F2-D200 11 : 50 : 24*,a 08 : 46 : 31** 13 : 51 : 21n.s. 32 : 147 : 66***
heterogeneity n.s. * n.s. **
∑F2 34 : 91 : 54n.s. — 32 : 112 : 35** —
Open in a new tab

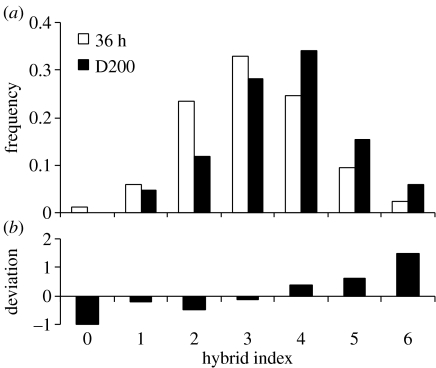
Two hundred days after fertilization, genotype frequencies at locus EFbis departed significantly from the Mendelian expectation (table 2). Pooling the results across loci, genotype frequencies significantly departed from the Mendelian expectation. A significant heterogeneity in genotype frequencies was observed at locus EFbis and in the pooled dataset. The single-locus trend was visible at the multilocus level and is illustrated in figure 2. Heterogeneity of multilocus genotypic frequencies among time samples was significant (p<0.001), primarily as a consequence of directional selection favouring genotypes with the highest hybrid indexes (i.e. genotypes with a high number of G alleles, see figure 2). In addition, strong and significant pairwise associations across loci appeared at this stage (table 3), suggesting epistatic interactions between the chromosome fragments mapped by our markers. Interestingly, selection did not result in significant heterozygote deficiencies (table 3). Note that contrary to backcrosses we detected differences in genotype frequencies between the early larval stage and the juvenile stage (e.g. figure 2), which provide unequivocal evidence of differential mortalities.

Figure 2.

Figure 2

Open in a new tab

(a) Tri-locus hybrid index distributions in the F2 generation, 36 h and 200 days after fertilization; and (b) deviation from the Mendelian expectation with no linkage in the D200 sample.

Table 3.

Pairwise associations of alleles within loci (heterozygote deficiency) and between loci (linkage disequilibrium), and confidence interval, 200 days after fertilization in the F2.

mac-1/EFbis Glu-5′/EFbis Glu-5′/mac-1 tri-locus
heterozygote deficiency (95% CI) −0.03 (−0.05; 0) −0.02 (−0.06; 0) −0.03 (−0.06; 0) −0.02 (−0.05; 0)
linkage disequilibrium (95% CI) 0.11 (0.06; 0.12) 0.07 (0.01; 0.1) 0.07 (0; 0.1) 0.06 (0.04; 0.09)
Open in a new tab

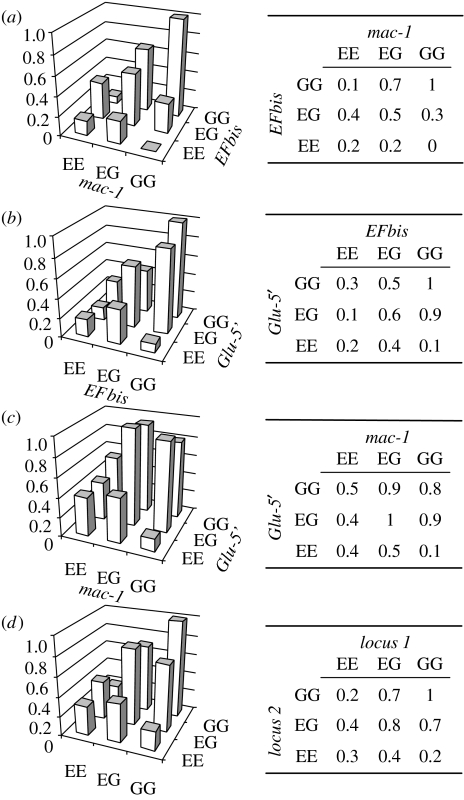
(d) Bi-locus fitness landscapes

Our sample size did not allow drawing tri-locus fitness landscapes with confidence, and we present here the three bi-locus fitness landscapes (figure 3a–c). As already observed with the hybrid index distribution, we observed a tendency for an advantage towards genotypes with more G alleles. However, epistatic interactions were visible in addition to directional selection. The least fit genotype always was an EE homozygote at one locus and a GG homozygote at the other. The two homozygous–homozygous recombined genotypes, EEGG and GGEE, were always less fit than the double heterozygote (EGEG), while these three genotypes have the same hybrid index. Finally, at least one of the homozygous–homozygous hybrid genotypes was less fit than the parental edulis genotype (EEEE), although a simple additive effect of the dose of G alleles would predict the reverse.

Figure 3.

Figure 3

Open in a new tab

(a–c) Bi-locus fitness landscapes in the F2 generation. (d) Averaged pairwise landscape obtained by considering symmetrical genotypes (e.g. EEGG and GGEE) to be identical.

The genotype space produced in an F2 is different than in a backcross: in a backcross genomes are mosaics of GG homozygous and EG heterozygous chromosome portions, while in F2s some chromosome chunks are EE homozygous. A closer look at the averaged bi-locus landscape (figure 3d) would provide an explanation as to why selection was not as easily detected in backcrosses as it was in the F2s. Although in a different genetic background (without EE homozygous portions), only the four top-right genotypes of the landscape were produced in backcrosses—their fitnesses were not very different when compared to the fitnesses of the other five genotypes additionally produced in the F2s.

(e) Modelling a hybrid zone with the observed fitness landscape

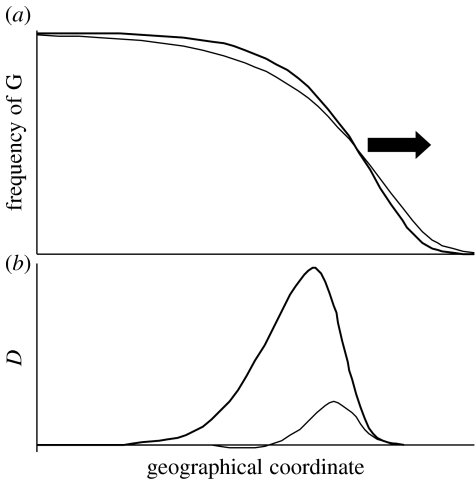
We used the averaged pairwise fitness landscape (see figure 3d) to run our two-locus model. Our model is of course too simple to depict the complexity of the Mytilus hybrid zone. Among many other things, it only considers a pair of loci while epistatic interactions potentially rely on more loci and each locus cumulates indirect selective effects from other loci in multilocus clines (Barton 1983). Furthermore, the fitness landscapes in figure 3 are rough estimates for which a surrogate of fitness is measured (larval survival), in a single artificial environment and the pattern obscured by unknown recombination rates between markers and fitness loci. However, such a model is still useful to make some basic observations. First, the resulting hybrid zone is not stable: we observed a wave of advance of G alleles resulting in their ultimate fixation in all demes. Second, the consequences of epistasis can be evaluated by comparing the results based on the observed fitness landscape to those obtained under a fully additive model. In the additive model, the fitness was defined as W=1−Hs, where H is the hybrid index of the genotype (0–4) and s is the selective coefficient. We used s=0.175 so that the fitness of the EEEE matched the observed value of 0.3. As shown in figure 4a, the additive model generates somewhat less steep and less symmetric clines and a slightly faster wave of advance (3% faster, not shown). The main difference between additive and non-additive models lies with linkage disequilibria (figure 4b), which are much smaller in the additive model and even slightly negative in the tail of the cline. In contrast, linkage disequilibria are strong and always positive with the observed fitness landscape, implying limited recombination between parental genomes and a strong barrier to neutral gene flow.

Figure 4.

Figure 4

Open in a new tab

Cline shapes and linkage disequilibria, D, obtained from a simple two-locus one-dimensional stepping-stone model. The black arrow gives the direction of propagation of waves of advance. Bold lines are the results obtained with the averaged pairwise landscape of figure 3d. Thin lines are the results obtained with an additive model with a selection coefficient of 0.175.

4. Discussion

We have studied the segregation of three marker loci in second generations of hybridization between M. edulis and M. galloprovincialis. We did not detect evidence of physical linkage between the three loci which segregated independently in the early larval stage. We found evidence of two sorts of selection: (i) directional selection favouring M. galloprovincialis genotypes and (ii) dominance by dominance epistatic interactions expressed in multi-homozygous recombinant genotypes.

Our results add to the already long list of studies that found a fitness advantage of M. galloprovincialis genotypes over M. edulis ones (Skibinski 1983; Coustau et al. 1991b; Gardner 1994a; Hilbish et al. 1994; reviewed in Gardner 1994b). Interestingly, the conditions under which a reciprocal advantage of M. edulis genotypes could be expressed remain to be found. In contrast with our previous experiment (Bierne et al. 2002a), our rearing facilities in La Tremblade should a priori have favoured M. edulis genotypes according to the genetic composition of natural populations surrounding the hatchery and the relatively low salinity of the water (27‰). As a consequence, the hypothesis of an intrinsic advantage to M. galloprovincialis in a broad set of environmental conditions should be seriously considered.

The second type of selection was epistasis. Strong and significant pairwise associations among loci appeared after 200 days of larval and juvenile life in the F2s. Sampling the early larval stage allowed us to tell apart the effect of epistatic selection from physical linkage in the interpretation of our results, a distinction that was not possible previously with allozyme markers (Hilbish et al. 1994). Bi-locus fitness landscapes presented in figure 3 visibly depart from a simple additive model as the least fit genotype was always either one or the other homozygous–homozygous hybrid genotypes (EEGG and GGEE), despite their having one half of their alleles of the G type. Our markers are thus linked to recessive DM substitutions. The predominantly recessive nature of DM substitutions is also supported in our experiment by the stronger larval mortalities observed in the F2s, while other treatments, including backcrosses, presented consistently lower mortalities (table 1). We acknowledge, however, that this latter result cannot be rigorously disentangled from a tank effect.

The ease of detecting pairs of DM substitutions with only three markers and for each of the three pairs of marker is very surprising. This result suggests that a high number of recessive DM substitutions have accumulated in the genome of these two mussel taxa. Indeed, our design was unlikely to detect incompatibilities if they were due to only two or a few loci because the three markers together mark a small proportion of the genome—knowing that the haploid chromosome number is 14 in Mytilus (Ahmed & Sparks 1970) and considering 1–3 chiasmata per bivalent, roughly 2–5% of the genome is marked by each locus in the F2 generation. Our data suggest that any marker is likely to be linked to a DM substitution, which means there is at least one DM locus per chromosome. Furthermore, any pair of chromosomes seems to contain a pair of interacting DM loci. This suggests that either more than two loci on different chromosomes are involved in multi-way epistatic interactions, or many DM loci are present on each chromosome, each being involved in a pairwise interaction.

The recessivity of DM substitutions between the two mussel taxa is in accordance with Turelli & Orr's (1995) dominance theory of post-zygotic isolation. An important drawback of this theory is that we still have little explanation to why DM substitutions should be recessive (Orr & Presgraves 2000). Interestingly, Kondrashov et al. (2002) and Welch (2004) have recently argued that DM substitutions may be originally mildly deleterious mutations that become positively selected as a consequence of a substitution at another locus. DM alleles could thus be recruited from the standing pool of segregating deleterious mutations, most of which are usually recessive. Here, attention might be called to the fact that marine bivalves have one of the highest deleterious mutation loads ever reported in the animal kingdom to date (Bierne et al. 1998; Launey & Hedgecock 2001). Note, however, that the recessive effects of DM substitutions on hybrid fitness do not necessarily mean that they were recessive in the genetic context corresponding to their fixation.

How do the two types of selection, directional and epistatic, combine in the mussel hybrid zone? More precisely, are epistatic interactions sufficiently strong to generate a stable hybrid zone? This is a difficult question to answer. Our simple two-locus model suggests that the magnitude of epistasis detected in our experiment is not sufficient to prevent the replacement of M. edulis by M. galloprovincialis. Unless M. edulis compensates its weakness by an advantage in another, still unexplored, component of fitness, the Mytilus hybrid zone is thus expected to move. It does not mean that the movement should be visible at a time-scale of years or even decades. Furthermore, in the mosaic zone of Mytilus the movement would not necessarily be a wave of advance, but could proceed by jumps owing to stochastic dispersal and/or selection in a heterogeneous environment. Evidence for moving hybrid zones is usually indirect (Moran 1981; Rohwer et al. 2001; Cruzan 2005) and exploit the theoretical prediction that waves of advance are expected to leave a footprint in the form of asymmetrical introgression (Barton & Hewitt 1985). We here suggest that a strong barrier to neutral gene flow generated by the superposition of epistasis on directional selection may partly mask the effect. A closer look at allele frequencies observed in natural populations at the three markers used would, however, reveal a slight tendency for asymmetrical introgression (Bierne et al. 2003c), which would be in accordance with a northward progression of the mussel hybrid zone.

To finish with, we need to find explanations as to why endogenous hybrid depression has not easily been detected in Mytilus previously. In our view, this results from the fact that the fitness of hybrids has previously been investigated through correlations between phenotypes and genotypes at marker loci in natural populations. These studies may miss important patterns for several reasons. (i) For a genetic barrier to neutral gene flow to be effective, hybrids need to be rare in natural populations (Barton & Bengtsson 1986). (ii) If hybrids are found to be frequent they probably are irrelevant introgressed genotypes, i.e. repeated interbreeding may have locally decreased the linkage disequilibrium between marker loci and selected loci to the point that patterns of selection on the latter are hardly visible on the former. (iii) In mosaic hybrid zones, local parental populations are more introgressed at neutral loci than external populations; however, the latter have traditionally been used as references, which may lead to misidentification of parental genotypes as recently recombined hybrids (Bierne et al. 2002b). (iv) Only adult patterns of mortality and growth have been investigated while most of the developmental processes and mortality take place during the larval phase and metamorphosis. On the other hand, artificial crossing allowed us to produce a high number of well-defined genotypes. Evidence for the existence of endogenous post-zygotic selection distributed on many loci of small effects may provide the missing factor explaining the persistence—at least in the short term—and strength of barriers to neutral introgression in Mytilus hybrid zones.

Acknowledgments

The authors are indebted to P. Phélipot for the larval rearing in La Tremblade. They thank P. Borsa, C. Daguin, B. Godelle and M. Valero for helpful discussions and two anonymous referees for insightful comments. This research was funded in part by contract no. IFREMER URM 16.

Supplementary Material

Tables S1 and S2
rspb20053440s04.pdf (49.3KB, pdf)

References

  1. Ahmed M, Sparks A.K. Chromosome number, structure and autosomal polymorphism in the marine mussels Mytilus edulis and Mytilus californianus. Biol. Bull. 1970;138:1–13. [Google Scholar]
  2. Barton N.H. Multilocus clines. Evolution. 1983;37:454–471. doi: 10.1111/j.1558-5646.1983.tb05563.x. [DOI] [PubMed] [Google Scholar]
  3. Barton N.H. Estimating multilocus linkage disequilibria. Heredity. 2000;84:373–389. doi: 10.1046/j.1365-2540.2000.00683.x. 10.1046/j.1365-2540.2000.00683.x [DOI] [PubMed] [Google Scholar]
  4. Barton N.H. The role of hybridization in evolution. Mol. Ecol. 2001;10:551–568. doi: 10.1046/j.1365-294x.2001.01216.x. 10.1046/j.1365-294x.2001.01216.x [DOI] [PubMed] [Google Scholar]
  5. Barton N.H, Bengtsson B.O. The barrier to genetic exchange between hybridising populations. Heredity. 1986;56:357–376. doi: 10.1038/hdy.1986.135. [DOI] [PubMed] [Google Scholar]
  6. Barton N.H, Hewitt G.M. Analysis of hybrid zones. Annu. Rev. Ecol. Syst. 1985;16:113–148. 10.1146/annurev.es.16.110185.000553 [Google Scholar]
  7. Beaumont A.R, Abdul-Matin A.K.M, Seed R. Early development, survival and growth in pure and hybrid larvae of Mytilus edulis and M. galloprovincialis. J. Mollus. Stud. 1993;59:120–123. [Google Scholar]
  8. Beaumont A.R, Turner G, Wood A.R, Skibinski D.O.F. Hybridisations between Mytilus edulis and Mytilus galloprovincialis and performance of pure species and hybrid veliger larvae at different temperatures. J. Exp. Mar. Biol. Ecol. 2004;302:177–188. 10.1016/j.jembe.2003.10.009 [Google Scholar]
  9. Bierne N, Launey S, Naciri-Graven Y, Bonhomme F. Early effect of inbreeding as revealed by microsatellite analyses on Ostrea edulis larvae. Genetics. 1998;148:1893–1906. doi: 10.1093/genetics/148.4.1893. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Bierne N, David P, Boudry P, Bonhomme F. Assortative fertilization and selection at larval stage in the mussels Mytilus edulis and M. gallopovincialis. Evolution. 2002a;56:292–298. doi: 10.1111/j.0014-3820.2002.tb01339.x. [DOI] [PubMed] [Google Scholar]
  11. Bierne N, David P, Langlade A, Bonhomme F. Can habitat specialisation maintain a mosaic hybrid zone in marine bivalves? Mar. Ecol. Prog. Ser. 2002b;245:157–170. [Google Scholar]
  12. Bierne N, Bonhomme F, David P. Genetics at larval stage in marine bivalves. In: Fingerman M, Nagabhushanam R, editors. Recent advances in marine biotechnology. vol. 10. Science Publishers; Enfield, NH: 2003a. pp. 239–262. [Google Scholar]
  13. Bierne N, Bonhomme F, David P. Habitat preference and the marine speciation paradox. Proc. R. Soc. B. 2003b;270:1399–1406. doi: 10.1098/rspb.2003.2404. 10.1098/rspb.2003.2404 [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Bierne N, Borsa P, Daguin C, Jollivet D, Viard F, Bonhomme F, David P. Introgression patterns in the mosaic hybrid zone between Mytilus edulis and M. galloprovincialis. Mol. Ecol. 2003c;12:447–462. doi: 10.1046/j.1365-294x.2003.01730.x. 10.1046/j.1365-294X.2003.01730.x [DOI] [PubMed] [Google Scholar]
  15. Charlesworth B, Coyne J.A, Barton N.H. The relative rates of evolution of sex-chromosomes and autosomes. Am. Nat. 1987;130:113–146. 10.1086/284701 [Google Scholar]
  16. Coustau C, Renaud F, Delay B. Genetic characterization of the hybridization between Mytilus edulis and M. galloprovincialis on the Atlantic coast of France. Mar. Biol. 1991a;111:87–93. 10.1007/BF01986350 [Google Scholar]
  17. Coustau C, Renaud F, Maillard C, Pasteur N, Delay B. Differential susceptibility to a trematode parasite among genotypes of the Mytilus edulis/galloprovincialis complex. Genet. Res. 1991b;57:207–212. doi: 10.1017/s0016672300029359. [DOI] [PubMed] [Google Scholar]
  18. Coyne J.A, Orr H.A. The evolutionary genetics of speciation. Phil. Trans. R. Soc. B. 1998;353:287–305. doi: 10.1098/rstb.1998.0210. 10.1098/rstb.1998.0210 [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Cruzan M.B. Patterns of introgression across an expanding hybrid zone: analysing historical patterns of gene flow using nonequilibrium approaches. New Phytol. 2005;167:267–278. doi: 10.1111/j.1469-8137.2005.01410.x. 10.1111/j.1469-8137.2005.01410.x [DOI] [PubMed] [Google Scholar]
  20. Daguin C, Bonhomme F, Borsa P. The zone of sympatry and hybridization of Mytilus edulis and M. galloprovincialis, as described by intron length polymorphism at locus mac-1. Heredity. 2001;86:342–354. doi: 10.1046/j.1365-2540.2001.00832.x. 10.1046/j.1365-2540.2001.00832.x [DOI] [PubMed] [Google Scholar]
  21. Dobzhansky T. Columbia University Press; New York, NY: 1937. Genetics and the origin of species. [Google Scholar]
  22. Edmands S. Heterosis and outbreeding depression in interpopulation crosses spanning a wide range of divergence. Evolution. 1999;53:1757–1768. doi: 10.1111/j.1558-5646.1999.tb04560.x. [DOI] [PubMed] [Google Scholar]
  23. Ernande B, Clobert J, McCombie H, Boudry P. Genetic polymorphism and trade-offs in the early life-history strategy of the Pacific oyster, Crassostrea gigas (Thunberg, 1795): a quantitative genetic study. J. Evol. Biol. 2003;16:399–414. doi: 10.1046/j.1420-9101.2003.00543.x. 10.1046/j.1420-9101.2003.00543.x [DOI] [PubMed] [Google Scholar]
  24. Feldman M.W, Christiansen F.B. The effect of population subdivision on two loci without selection. Genet. Res. 1974;24:151–162. doi: 10.1017/s0016672300015184. [DOI] [PubMed] [Google Scholar]
  25. Gardner J.P.A. The Mytilus edulis species complex in Southwest England: multilocus heterozygosity, background genotype and a fitness correlate. Biochem. Syst. Ecol. 1994a;22:1–11. 10.1016/0305-1978(94)90109-0 [Google Scholar]
  26. Gardner J.P.A. The structure and dynamics of naturally occurring hybrid Mytilus edulis and M. galloprovincialis (Bivalvia, Mollusca) populations: review and interpretation. Arch. Hydrobiol. 1994b;99:37–71. [Google Scholar]
  27. Gardner J.P.A, Skibinski D.O.F. Genotype-dependant fecundity and temporal variation of spawning in hybrid mussel populations. Mar. Biol. 1990;105:153–162. 10.1007/BF01344281 [Google Scholar]
  28. Gavrilets S. Princeton university press; Princeton, NJ: 2004. Fitness landscapes and the origin of species. [Google Scholar]
  29. Gosling E.M, McGrath D. Genetic variability in exposed-shores mussels Mytilus spp. along an environmental gradient. Mar. Biol. 1990;104:413–418. 10.1007/BF01314344 [Google Scholar]
  30. Haldane J.B.S. Sex-ratio and unidirectional sterility in hybrid animals. J. Genet. 1922;12:101–109. [Google Scholar]
  31. Hilbish T.J, Bayne B.L, Day A. Genetics of the physiological differentiation within the marine mussel Mytilus. Evolution. 1994;48:267–286. doi: 10.1111/j.1558-5646.1994.tb01311.x. [DOI] [PubMed] [Google Scholar]
  32. Kondrashov A.S, Sunyaev S, Kondrashov F.A. Dobzhansky–Muller incompatibilities in protein evolution. Proc. Natl Acad. Sci. USA. 2002;99:14878–14883. doi: 10.1073/pnas.232565499. 10.1073/pnas.232565499 [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Launey S, Hedgecock D. High genetic load in the Pacific oyster Crassostrea gigas. Genetics. 2001;159:255–265. doi: 10.1093/genetics/159.1.255. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Laurie C.C. The weaker sex is heterogametic: 75 years of Haldane's rule. Genetics. 1997;147:937–951. doi: 10.1093/genetics/147.3.937. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Moran C. Genetic demarcation of geographical distribution by hybrid zones. Proc. Ecol. Soc. Aust. 1981;11:67–73. [Google Scholar]
  36. Muller H.J. Bearing of the Drosophila work on systematics. In: Huxley J, editor. The new systematics. Clarendon Press; Oxford, UK: 1940. pp. 185–268. [Google Scholar]
  37. Muller H.J. Isolating mechanisms, evolution and temperature. Biol. Symp. 1942;6:71–125. [Google Scholar]
  38. Ohresser M, Borsa P, Delsert C. Intron-length polymorphism at the actin-gene locus mac-1: a genetic marker for populations studies in the marine mussels Mytilus galloprovincialis and M. edulis. Mol. Mar. Biol. Biotechnol. 1997;6:123–130. [PubMed] [Google Scholar]
  39. Orr H.A. The population genetics of speciation: the evolution of hybrid incompatibilities. Genetics. 1995;139:1805–1813. doi: 10.1093/genetics/139.4.1805. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Orr H.A, Presgraves D.C. Speciation by postzygotic isolation: forces, genes and molecules. Bioessays. 2000;22:1085–1094. doi: 10.1002/1521-1878(200012)22:12<1085::AID-BIES6>3.0.CO;2-G. 10.1002/1521-1878(200012)22:12%3C1085::AID-BIES6%3E3.0.CO;2-G [DOI] [PubMed] [Google Scholar]
  41. Orr H.A, Turelli M. The evolution of postzygotic isolation: accumulating Dobzhansky–Muller incompatibilities. Evolution. 2001;55:1085–1094. doi: 10.1111/j.0014-3820.2001.tb00628.x. [DOI] [PubMed] [Google Scholar]
  42. Rawson P.D, Joyner K.L, Meetze K, Hilbish T.J. Evidence for intragenic recombination within a novel genetic marker that distinguishes mussels in the Mytilus edulis species complex. Heredity. 1996;77:599–607. doi: 10.1038/hdy.1996.187. [DOI] [PubMed] [Google Scholar]
  43. Raymond M, Rousset F. GENEPOP (ver. 1.2): a population genetics software for exact test and ecumenicism. J. Hered. 1995;86:248–249. [Google Scholar]
  44. Rice W.R. Analyzing tables of statistical tests. Evolution. 1989;43:223–225. doi: 10.1111/j.1558-5646.1989.tb04220.x. [DOI] [PubMed] [Google Scholar]
  45. Rieseberg L.H, Buerkle C.A. Genetic mapping in hybrid zones. Am. Nat. 2002;159:S36–S50. doi: 10.1086/338371. 10.1086/338371 [DOI] [PubMed] [Google Scholar]
  46. Rohwer S, Bermingham E, Wood C. Plumage and mitochondrial DNA haplotype variation across a moving hybrid zone. Evolution. 2001;55:405–422. doi: 10.1111/j.0014-3820.2001.tb01303.x. [DOI] [PubMed] [Google Scholar]
  47. Secor C.L, Day A.J, Hilbish T.J. Factors influencing differential mortality within a marine mussel (Mytilus spp.) hybrid population in southwestern England: reproductive effort and parasitism. Mar. Biol. 2001;138:731–739. 10.1007/s002270000418 [Google Scholar]
  48. Skibinski D.O.F. Natural selection in hybrid mussel populations. In: Rollinson O, editor. Protein polymorphism: adaptative and taxonomic significance. Systematics Association special volume no. 24. Academic Press; London, UK: 1983. pp. 283–299. [Google Scholar]
  49. Skibinski D.O.F, Beardmore J.A, Cross T.F. Aspects of the population genetics of Mytilus (Mytilidae; mollusca) in the British Isles. Biol. J. Linn. Soc. 1983;19:137–183. [Google Scholar]
  50. Slatkin M. Gene flow and selection in a two-locus system. Genetics. 1975;81:787–802. doi: 10.1093/genetics/81.4.787. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Turelli M, Orr H.A. The dominance theory of Haldane's rule. Genetics. 1995;140:389–402. doi: 10.1093/genetics/140.1.389. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Turelli M, Orr H.A. Dominance, epistasis and the genetics of postzygotic isolation. Genetics. 2000;154:1663–1679. doi: 10.1093/genetics/154.4.1663. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Welch J.J. Accumulating Dobzhansky–Muller incompatibilities: reconciling theory with data. Evolution. 2004;58:1145–1156. doi: 10.1111/j.0014-3820.2004.tb01695.x. [DOI] [PubMed] [Google Scholar]
  54. Wilhelm R, Hilbish T.J. Assessment of natural selection in a hybrid population of mussels: evaluation of exogenous vs. endogenous selection models. Mar. Biol. 1998;131:505–514. 10.1007/s002270050342 [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Tables S1 and S2
rspb20053440s04.pdf (49.3KB, pdf)

Articles from Proceedings of the Royal Society B: Biological Sciences are provided here courtesy of The Royal Society

RESOURCES