Abstract
When interactions with heterospecifics prevent females from identifying conspecific mates, natural selection can promote the evolution of mating behaviours that minimize such interactions. Consequently, mating behaviours may diverge among conspecific populations in sympatry and in allopatry with heterospecifics. This divergence in conspecific mating behaviours—reproductive character displacement—can initiate speciation if mating behaviours become so divergent as to generate reproductive isolation between sympatric and allopatric conspecifics. We tested these ideas by using artificial neural networks to simulate the evolution of conspecific mate recognition in populations sympatric and allopatric with different heterospecifics. We found that advertisement calls diverged among the different conspecific populations. Consequently, networks strongly preferred calls from their own population to those from foreign conspecific populations. Thus, reproductive character displacement may promote reproductive isolation and, ultimately, speciation among conspecific populations.
Keywords: sexual signals, mate choice, reinforcement, speciation, species recognition
1. Introduction
When species with similar sexual signals co-occur, selection may favour divergence of these signals to minimize either their interference or the risk of mis-mating between species (Howard 1993; Andersson 1994; Servedio & Noor 2003; Coyne & Orr 2004). This selective process results in mating behaviours that are not only divergent between species that co-occur but that are also divergent among conspecific populations that do and do not occur with heterospecifics or that co-occur with different heterospecifics (a pattern termed reproductive character displacement; reviewed in Howard 1993; Andersson 1994; Gerhardt & Huber 2002; Coyne & Orr 2004; e.g. Noor 1995; Saetre et al. 1997; Pfennig 2000; Gabor & Ryan 2001; Höbel & Gerhardt 2003).
Yet as mating behaviours diverge between conspecific populations that do and do not occur with a given heterospecific, individuals may fail to accept conspecifics from the alternative population type as mates. If so, these conspecific populations may become reproductively isolated, and they may ultimately undergo speciation as a result (Howard 1993; e.g. Hoskin et al. 2005). In this way, reproductive character displacement may initiate speciation (Howard 1993; Hoskin et al. 2005).
We tested these ideas by using artificial neural networks to simulate the evolution of mating behaviours in response to different heterospecific interactions. We specifically sought to evaluate whether such interactions would promote divergence in advertisement signals and generate assortative mating within conspecific populations that could result in reproductive isolation.
2. Material and methods
Our model simulated the evolution of species recognition and male advertisement signals in three populations that differed in whether they co-occurred with a given heterospecific. At the end of the simulations, we evaluated whether the advertisement signals had diverged. We also determined whether the networks discriminated against the evolved calls from alternative conspecific populations. We mimicked a system in which males use pulsatile calls to attract females as mates (as occurs in many anuran and insect systems; Gerhardt & Huber 2002). Although we simulated species recognition for acoustic signals, our results potentially can be generalized to other sensory modalities.
We generated three population types consisting solely of networks belonging to the same species, ‘species A’. Depending on the population type, the networks evolved conspecific recognition of advertisement signals of species A in the face of no heterospecific signals or when faced with discrimination of signals from their own species versus signals from one of two heterospecific species. In particular, in one population type, networks were selected for the ability to discriminate representations of conspecific acoustic stimuli of species A from white noise. The white noise stimulus controlled for the presence of a second stimulus and provided a means of assaying the networks' recognition of a conspecific signal. We refer to this population type as ‘A’. This population mimics the evolution of conspecific recognition in the absence of heterospecifics. In the second population type, species A networks evolved to discriminate between conspecific stimuli of species A and stimuli of a heterospecific, species B. We refer to this population type as ‘AB’. Finally, in a third population type, networks evolved to discriminate between conspecific stimuli of species A and stimuli from a second heterospecific, species C. We refer to this population type as ‘AC.’
(a) The model
We used artificial neural networks, which consist of units (‘neurons’) interconnected in varying degrees into a larger network (see Enquist & Ghirlanda 2005 for full description of neural networks). We used the Elman network architecture (Elman 1990) available with Matlab's neural network toolbox (Demuth & Beale 1997) to generate our networks. Each network processed the stimuli by a single hidden layer of neurons. Responses from this hidden layer were then fed forward to an output layer. Elman networks are particularly effective at decoding stimuli that are temporally structured (e.g. acoustic stimuli) because the Elman architecture includes recurrent connections within the hidden layer (Elman 1990; Demuth & Beale 1997; e.g. Ryan & Getz 2000). This recurrence enables networks to process information in a current time-step contingent on information from a preceding time-step. Evolutionary simulations using a similar kind of network have predicted female preferences for both conspecific and heterospecific male calls in túngara frogs (Physalaemus pustulosus, Phelps & Ryan 1998, 2000; Phelps et al. 2001).
The activity of the hidden layer, a1, was determined using a hyperbolic transfer function as follows (notation here and below is that of Demuth & Beale 1997):
| 2.1 |
where p was a 35×1 vector from the input layer corresponding to the kth column from the signal matrix, which had 35 rows corresponding to different frequencies in the signal and 190 columns corresponding to time (see below for details of signal properties). IW1,1 was a 23×35 matrix corresponding to 23 neurons responding to 35 frequency bands of the stimulus input, LW1,1 was a 23×35 matrix that constituted weights of the recurrent connections in the hidden layer and b1 was a 23×1 bias vector (Demuth & Beale 1997). Biases enable networks to better represent relationships between a signal and output (Demuth & Beale 1997). The bias vectors were subject to mutation and so could evolve in our simulations.
The activity of the output layer, a2, was generated from a pure linear transfer function as follows:
| 2.2 |
where LW2,1 was a 1×23 matrix that constituted the weights of the connections to the hidden layer and b2 was a 23×1 bias vector. The resulting output was a vector of responses corresponding to each column in the signal matrix. We summed this vector to obtain a single scalar response measure to the entire signal matrix. For further details of the network architecture, see Demuth & Beale (1997), Ryan & Getz (2000) and Pfennig & Ryan (in press).
We used a genetic algorithm to simulate the evolution of conspecific recognition. For each population type, we created 100 networks consisting of the above architecture. The matrix values for each network were uniform random values constrained to range between −1 and 1. We then presented each network a conspecific stimulus and either a noise stimulus or one of two different heterospecific stimuli, depending on whether the network was from an A, AB or AC population. We defined the fitness of a network as the difference between its response to the conspecific stimulus and its response to the heterospecific (or noise) stimulus. Consequently, those networks better able to discriminate between conspecifics and heterospecifics had higher fitness. Negative fitness values were truncated to zero.
The probability that a network was passed to the next generation was weighted by its fitness: networks with higher fitness were more likely represented in the next generation than networks with lower fitness. Using this procedure, at each generation we selected 100 networks at random with replacement from the networks in the preceding generation. Additionally, the conspecific male calls that had been presented to these networks were also selected and passed on to the next generation (see §2b). In this way, the conspecific male calls also evolved.
Following this selection process, all networks (except a single network with the highest fitness in the previous generation) underwent mutation. Leaving the top network unmutated speeds the evolutionary algorithm, but does not appear to alter the outcome of the model. Values from the layer matrices and bias vectors of each network were chosen for mutation with a probability of 0.001. For those values that were chosen for mutation, we added a random value between −0.5 and 0.5 to the existing value in each matrix element. Any values that exceeded 1.0 or were less than −1.0 were truncated to 1.0 and −1.0, respectively. Prior work altering the nature of mutation shows that it appears not to influence the outcome of the simulations.
We repeated this process for 200 generations and then replicated the entire procedure 30 times for each population type. Both the mean population fitness and maximum fitness for all replicates reached a plateau by generation 200.
(b) Male calls
The networks were presented pulsatile calls in a frequency by time matrix in which the values within the matrix ranged from 0 to 1 and represented amplitude of the signal at a given frequency and time (analogous to a sonogram; see also Phelps & Ryan 1998, 2000; Phelps et al. 2001). We synthesized the calls using a program written in Matlab that generated each call by combining randomly chosen values (see below) of four parameters: call duration (the length of the call in terms of matrix columns); call dominant frequency (the frequency in the call with the greatest energy, measured in terms of matrix rows); pulse rate (measured as number of pulses per matrix column) and inter-call interval (the number of matrix columns between the last column of the first call and the first column of the second call). Using this program, a new call was synthesized each time a call was presented to a network.
Each call was generated by randomly choosing parameter values to specify the call from the appropriate distributions for the conspecific or heterospecific calls. The initial distributions from which the parameters were drawn were normal distributions with the means and standard deviations in table 1. These distributions are modified distributions of actual call characters for three species of spadefoot toad that co-occur in southeastern Arizona, USA: Spea multiplicata, Spea bombifrons and Scaphiopus couchii (for actual call distributions see Pfennig 2000). We describe in detail why we chose these distributions and how they were modified elsewhere (Pfennig & Ryan in press). Using the randomly chosen parameters, each call was synthesized by initially generating a single triangular pulse. To do so, a value of 1 (the maximum value of amplitude in the signal matrix) was assigned in the row corresponding to the dominant frequency of the call at the column corresponding the onset of the call (the onset of the call in the call matrix was randomly determined). The values in adjacent rows and columns then degraded from one exponentially to create a triangular pulse. This pulse was then repeated to generate a single call with the appropriate duration and pulse rate. A gap of silence, where values of 0 were assigned to the columns corresponding to the inter-call interval, followed the call. At the end this interval, we appended a single pulse to indicate the onset of a second call.
Table 1.
Mean (±s.d.) of call parameters for each species, measured in terms of matrix columns or rows. (See text for description of how calls were generated. The values for species A were those in the initial generation and are therefore the parameters of the ‘ancestral A’ call. The call parameters of A, but not B or C, were allowed to evolve. See figure 1 for contrast of evolved A calls versus the ancestral A call.)
| call parameter | species | ||
|---|---|---|---|
| A | B | C | |
| call duration (cols.) | 62.6 (7.9) | 9.1 (0.7) | 62.4 (5.0) |
| inter-call interval (cols.) | 72.0 (1.7) | 64.8 (0.9) | 87.6 (4.7) |
| call pulse rate (pulses col−1.) | 0.05 (0.01) | 0.42 (0.05) | 0.34 (0.02) |
| dominant frequency (rows) | 15.6 (1.2) | 18.5 (1.2) | 18.4 (1.5) |
The white noise stimuli presented to networks in the A populations were generated by assigning uniform random values ranging from 0 to 1 to elements in a matrix that was the same size as that of the male calls. We also added noise to the male calls using the same procedure. The amplitude of all stimuli presented to the networks was standardized so that they were equal in total amplitude.
We allowed the conspecific male calls, but not the heterospecific calls, to evolve in our simulations. At each generation, the 100 conspecific calls associated with the 100 networks passed to the next generation were also passed to the next generation. From these calls, we obtained the mean and standard deviation for each call parameter. These new distributions were then used to generate the calls in the subsequent generation. Thus, in each generation, calls were randomly generated from the distribution of calls of the ‘sires’ in the previous generation. Calls were not pooled across replicates. Each replicate represented an independent evolutionary simulation of both species recognition and signal evolution.
For each replicate, we calculated the mean call parameters of the 100 calls in the final generation. These means were combined into a single data set along with call parameters of 30 randomly generated calls for each of the ancestral A population and B and C species. The randomly generated ancestral and heterospecific calls served as samples of these calls types.
We analysed these data using a principal component analysis, which generated two principal components that described the joint variation in the four parameters. Both principal components had eigenvalues greater than one. The first explained 52.8% of the variation in the advertisement calls, whereas the second explained 26.1% of the variation. We used these principal component values to compare the calls among the A, AB and AC populations based on the combined variation in the four call parameters. Because the data did not meet parametric assumptions, we compared each principal component among pairs of populations using Wilcoxon rank sums tests. We used a Bonferroni corrected alpha level of 0.017 in these multiple comparisons (Sokal & Rohlf 1995).
(c) Testing and analyses of networks' responses
We selected the network with the highest fitness from every eighth generation up through the last generation in each population type from each of the 30 replicates. We tested these networks for preferences of their own conspecific calls versus the heterospecific (or noise) stimulus with which they coevolved. More critically, we also assayed the responses of these networks to advertisement calls of their own population (local calls) versus those of the two alternative populations (foreign calls). In the tests described below, we used the male call distributions from the networks' own generation.
To test the networks' preferences for local calls versus the heterospecific (or noise) stimulus with which the networks coevolved, we presented each network with 100 pairs of a randomly generated call from its own population versus a randomly generated heterospecific or noise stimulus.
To test the networks' preferences for local calls versus foreign conspecific calls, we presented each network with two sets of calls. In one set, networks were presented local calls versus foreign calls from one of the alternative populations and in the second set, networks were presented local calls versus foreign calls from the second alternative population (e.g. A networks were presented A versus AB calls in one set and A versus AC in a second set). Thus, we generated six possible pairings of local and foreign calls. For each set, we presented 100 pairs of randomly generated local calls versus randomly generated foreign calls to each of the 30 networks in each population type.
In all tests of network preference, we calculated the difference in response between the local call and the alternative call. This raw measure of discrimination is analogous to the fitness measure used during the evolution of the networks. Because the magnitude of networks' discrimination differed not only across generations but also across independently evolved replicates and populations, we generated a relative measure of preference for local calls that was comparable among pairs of stimuli, generations, replicates and populations. To do so, we obtained the highest discrimination score expressed by any network at any time within that network's own replicate for the pairings of local calls versus the heterospecific calls with which they coevolved (i.e. B, C or noise). We then divided a network's raw discrimination scores for a given call pair by this maximum value for its replicate. As with our fitness measure, negative values were truncated to 0. We thereby generated a relative preference score for local calls in each pairing that varied from 0 to 1. At values close to 0, networks expressed no discrimination. At values approaching one, networks were expressing discrimination as strong as the highest level observed against heterospecifics (or noise) in that network's lineage. We, therefore, ascertained whether networks preferentially responded to local calls by comparing their average preference score in a given pair wise test with the null expectation of 0.
Although we found that the calls evolved to be divergent among the different population types (see §3), there was variation in the call parameters that evolved in different replicates within a given population type (especially in the AB and AC populations; see §3). Such variation could result from stochasticity in the simulations or may represent alternative solutions to similar discrimination tasks. We examined how networks responded to these call variants from other replicates of their same population type and compared this to their responses toward foreign calls from other populations. By doing so, we could discern whether networks selected against foreign calls because they were from alternative population types not just alternative replicates.
To make this comparison, we generated an average call for each replicate using the mean values of all four call parameters for the given replicate. We then presented each network with the average call from its own replicate (the local call) versus each alternative replicate (the foreign replicate call) from its own population type. Each network in each population was therefore presented 29 pairings of its local call with calls from different replicates. Preferences were scored as above. From these preference scores, we generated a mean preference for local calls within a given population type that we then used as a null expectation against which to compare the networks' preferences for local calls versus calls from alternative population types.
Finally, we examined whether network preferences for local calls were correlated with the similarity between local and foreign calls. To do so, we took the absolute difference between the principal component score of the average local call and the average foreign call presented to each network. We generated these values separately for both principal components. Because these data did not meet parametric assumptions, we used Spearman rank order correlation analysis to determine if the magnitude of difference between calls was associated with the average preference for local calls in a given pair type. These analyses utilized calls from across the independently evolved replicates and so reflect patterns, if any, associated with reproductive character displacement rather than variation within a single lineage.
3. Results
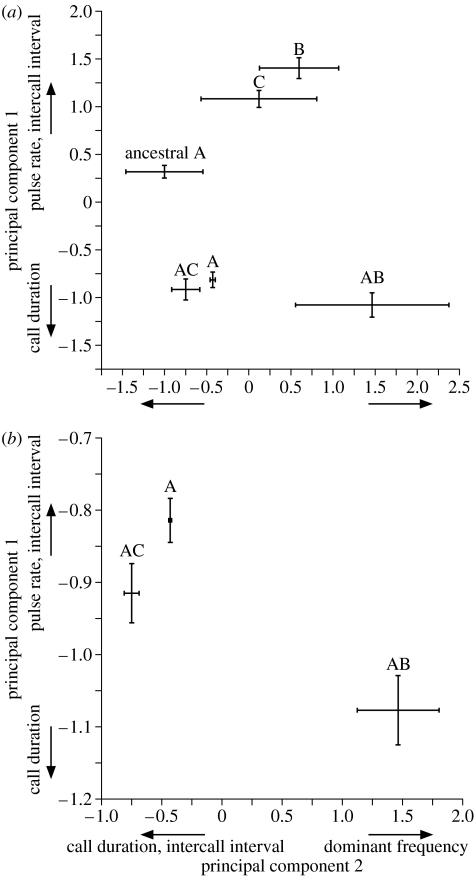
The divergence of signals among conspecific populations in response to heterospecifics could contribute to their reproductive isolation. We found that advertisement calls of all three populations evolved to be distinct from the ancestral call (figure 1a) and from each other (figure 1b). The principal component measures (PC1 and PC2) of the combined call parameters were both significantly different among the three populations (Wilcoxon normal approximation comparing PC1 among population pairs: A versus AC: Z=−4.07, p<0.0001; A versus AB: Z=−6.11, p<0.0001; AB versus AC: Z=5.45, p<0.0001; Wilcoxon normal approximation comparing PC2 among population pairs: A versus AC: Z=−5.73, p<0.0001; A versus AB: Z=5.34, p<0.0001; AB versus AC: Z=−5.79, p<0.0001; n=30 for each population).
Figure 1.
(a) Mean (±s.d.) for principal components that describe the combined variation in four call characters (dominant frequency, call duration, pulse rate and inter-call interval) for: the evolved calls from the three different conspecific populations (A, AB and AC), the heterospecific calls presented to the AB and AC populations during their evolution (B and C, respectively) and the initial conspecific call (ancestral A). Intersection of x-axis and y-axis standard deviation lines is the point of the mean for each. (b) Mean (±95%CI) for same principal components above comparing the evolved calls from A, AB and AC only. Non-overlapping confidence intervals indicate significant differences. Labels on axes indicate loading of call parameters on each principal component.
We used two measures to determine if the networks preferred local calls versus foreign calls. First, we compared mean preference for local calls with the null expectation of 0 (see §2). Networks from the three populations significantly preferred local calls to foreign calls (table 2; figure 2).
Table 2.
Network preferences for local calls versus foreign calls. (The network's population is also the population of the local call. The preference for local calls was assessed in two ways. First, mean response to local calls is compared with the null expectation of 0 if networks respond equally strongly to local and foreign calls. Second, mean response to local calls is compared to a null expectation that is the mean response to independently evolved calls from replicates of the networks' own population type. This latter contrast controlled for the possibility that networks may have been generally selective against foreign calls, not just those that diverged due to character displacement. Means and confidence intervals of preference strength for local calls from these pairings are displayed in figure 2.)
| network's population | population of foreign call | t29 (p value); H0: local call preference =0 | t29(p value), H0: local call preference=preference for calls from other replicatesa |
|---|---|---|---|
| A | AB | 21.48 (<0.0001)b | 17.96 (<0.0001)b |
| AC | 9.46 (<0.0001)b | 6.70 (<0.0001)b | |
| AB | A | 9.06 (<0.0001) | 3.24 (0.003) |
| AC | 10.72 (<0.0001) | 4.29 (0.0002) | |
| AC | A | 8.32 (<0.0001)b | −1.04 (0.31)b |
| AB | 10.58 (<0.0001) | 6.71 (<0.0001) |
Average preference for local calls when presented with calls from other replicates by networks in A; 0.027, AB; 0.310, AC; 0.203.
Analysis used transformed data to meet parametric assumptions.
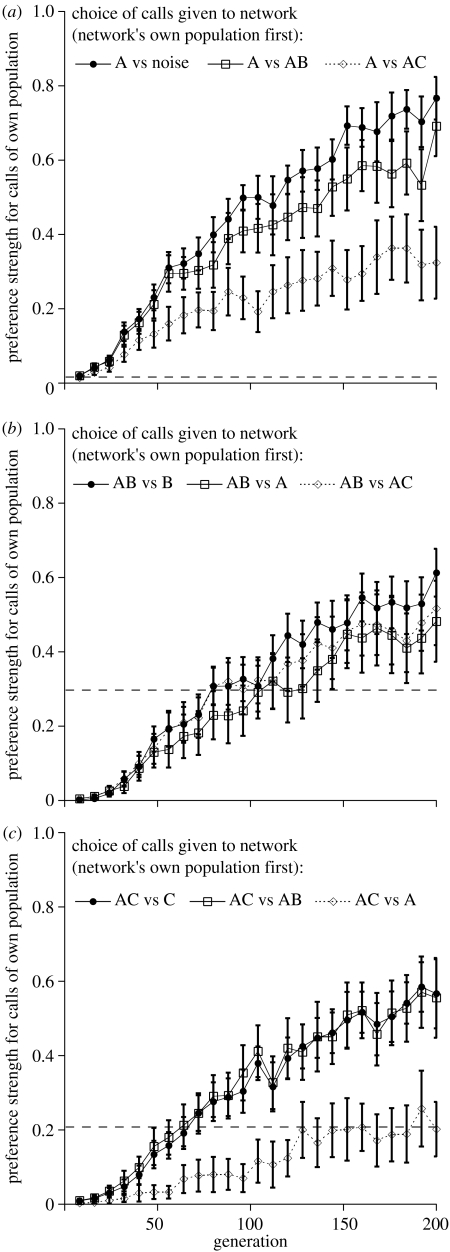
Figure 2.
Mean (±95% CI) preference for advertisement calls from networks' own population (local calls) versus calls of alternative populations (foreign calls) over time. (a) Results for A networks; (b) results for the AB networks and (c) results for AC networks. Non-overlapping confidence intervals indicate significant differences. Dashed horizontal line shows network preferences for local calls versus those from alternative replicates of same population type in final generation.
Divergence of populations could potentially result from stochastic variation in preferences and calls among independently evolved lineages rather than due to character displacement per se. To control for this possibility, we also compared networks' mean preferences for local calls when presented with foreign calls versus their mean preference for local calls when presented with independently evolved calls from alternative replicates of their own population type (see §2). We found that the A networks showed a weak preference for local calls versus calls from alternative replicates, whereas the AB and AC networks displayed relatively stronger preference for calls that evolved in their own replicate (figure 2).
Although the networks discriminated against calls from alternative replicates of their own population type, they generally showed even stronger preferences for local calls when they were paired with foreign population calls. In all but one pairing (AC networks presented with AC versus A calls), the networks discriminated against foreign calls significantly more strongly than they discriminated against calls from alternative replicates (table 2; figure 2).
The evolutionary trajectories of these preferences for local calls suggested that they arose in conjunction with the evolution of discrimination against the heterospecific calls (or noise) with which the networks coevolved (figure 2). Indeed, in all of the populations, networks in the final generation exhibited similarly strong discrimination against at least one type of foreign conspecific call as they exerted against the heterospecific calls with which they coevolved (figure 2).
This was exemplified in the AB population where we found no significant differences in preference for local conspecific calls among any of the three pairings presented to the networks (AB versus B calls, AB versus A calls and AB versus AC calls; F2,87=2.23, p=0.11; figure 2). In the A population, we found a significant difference in preference for local calls among the three possible pairings the A networks faced (F2,87=33.7, p<0.0001). The A networks, however, showed a similarly strong preference for locals calls when they were paired with AB calls as when local calls were paired with a white noise stimulus (as revealed by a Tukey–Kramer honestly significant difference (HSD) test, p>0.05; figure 2). The A networks showed significantly lower preference for local calls in the pairing of A and AC calls than in the other call pairings with which they were tested (Tukey–Kramer HSD test, p<0.05; figure 2).
Similarly, in the AC population, we found a significant difference in preference for local calls among the three possible pairings they faced (F2,87=15.9, p<0.0001). Yet, the AC networks showed a similarly strong preference for local calls when they were paired with AB calls as when local calls were paired with heterospecific C calls (as revealed by a Tukey–Kramer HSD test, p>0.05; figure 2). The AC networks showed significantly lower preference for local calls in the pairing of AC and A calls than in the other call pairings with which they were tested (Tukey–Kramer HSD test, p<0.05; figure 2).
The above results emphasize that the networks sometimes discriminated against foreign conspecific calls as strongly as they did heterospecific (or noise) stimuli. These findings also indicate that the networks did not necessarily respond to foreign calls from different population types in the same way. In both the A and AC populations, the networks discriminated against the foreign AB call more strongly than they selected against each other (figure 2). One explanation for this pattern is that because the A and AC calls were more similar (figure 1), they were less likely to discriminate against each other than against the AB calls. We investigated whether the differences in how networks responded to foreign calls could be attributed to the level of similarity between the local calls and a given foreign call type. For variation described by PC1, we found no associations between preference for local calls and dissimilarity of local and foreign calls (table 3). By contrast, we found that the greater the difference between local and foreign calls in PC2, the stronger the preference for local calls in four of the six pairings (table 3).
Table 3.
Correlation of preference strength for local calls with the absolute differences in principal component scores of local versus foreign calls, a measure of the similarity between the calls. (Spearman rank order correlation coefficient reported because data did not meet parametric assumptions. The network's population is also the population of the local call. n=30 for each correlation.)
| network's population | population of foreign call | rs (p-value) using difference in PC1 scores | rs (pvalue) using difference in PC2 scores |
|---|---|---|---|
| A | AB | −0.076 (0.69) | 0.195 (0.30) |
| AC | 0.092 (0.63) | −0.366 (0.047) | |
| AB | A | 0.060 (0.75) | 0.672 (<0.0001) |
| AC | 0.246 (0.19) | 0.393 (0.032) | |
| AC | A | −0.345 (0.062) | 0.528 (0.003) |
| AB | 0.126 (0.51) | 0.339 (0.067) |
4. Discussion
Using artificial neural network simulations, we found that advertisement calls diverged among populations in sympatry and allopatry with different heterospecifics. Moreover, we found that the networks preferred the advertisement calls of their own populations. As we discuss below, these findings suggest that reproductive character displacement can contribute to reproductive isolation among conspecific populations.
Although we observed divergence in male signals, call evolution was not strictly caused by differences in heterospecific interactions among the different populations. All three populations diverged dramatically from the ancestral call type (figure 1a). Such evolution may have occurred, if, e.g. certain call characters were more easily discriminated against the noisy background that all three populations experienced.
Despite their similar evolution relative to the ancestral calls, the calls of the different populations also diverged from one another (figure 1b). Interestingly, the calls that evolved in the populations that discriminated against heterospecifics were more variable (especially in AB) than those in the allopatric population, A (figure 1). Why this was so is unclear. One explanation is that there were few optimal calls for discriminating against noise alone, but many alternative call solutions for discriminating against a given heterospecific. Additional studies are required to evaluate why the observed pattern of variation arose and to ascertain the role of such variation in signal diversification and population divergence.
The population divergence in advertisement signals probably reflects divergence of network preferences for different signal characters in sympatry and allopatry with the different heterospecifics. In another study using this same modelling framework, we found that the networks evolved divergent preferences for aspects of conspecific advertisement signals among the three population types (Pfennig & Ryan in press). That heterospecifics can alter the nature of female preferences for conspecific signals is consistent with other studies (e.g. Gerhardt 1994; Saetre et al. 1997; Pfennig 2000; Ryan & Getz 2000; Höbel & Gerhardt 2003) and such different preferences could drive the evolutionary divergence of male signals among populations in sympatry and allopatry with different heterospecifics.
Perhaps most critically, we found that networks preferred calls of their own population to those from alternative conspecific populations (figure 2). Indeed, in some cases, the networks discriminated against foreign conspecific calls and heterospecific calls similarly. These results suggest that character displacement in mating behaviours such as male signals (arising from selection to avoid heterospecifics in sympatry but not allopatry) can in turn promote assortative mating within sympatric and allopatric conspecific populations. In a natural system, this pattern of mate choice could generate reproductive isolation and ultimately initiate speciation among conspecific populations (e.g. Hoskin et al. 2005).
Whether reproductive character displacement initiates speciation among conspecific populations depends on the degree to which it causes mating behaviours among them to diverge. Such divergence may be limited, however, if signals and mate preferences do not continue to diversify once the signals of the focal conspecific species are sufficiently distinct from those of heterospecifics (sensu Spencer et al. 1986). If so, reproductive character displacement may fail to promote sufficient divergence in mating behaviours that result in assortative mating within conspecific populations. We began our simulations with conspecific and heterospecific signals that were already somewhat divergent, however. Our study therefore suggests that reproductive character displacement may generate divergent conspecific signals even when conspecific and heterospecific signals are already distinct (figure 1).
Moreover, if reproductive character displacement initiates divergent patterns of runaway sexual selection between male signals and female preferences, conspecific populations become much more likely to diverge (sensu Lande 1981; Liou & Price 1994). Indeed, interactions with heterospecifics may alter not only traits used specifically in the context of species recognition, but may also alter the nature of sexual selection in populations that do and do not occur with heterospecifics (Gerhardt 1982; Ryan & Rand 1993; Pfennig 1998, 2000; Pfennig & Pfennig 2005). Thus, whether reproductive character displacement initiates speciation among conspecific populations may depend on how it alters the nature of sexual selection among them.
Speciation among conspecific populations that evolve divergent mating behaviours depending on the presence of heterospecifics may also become more likely if conspecific populations diverge in ways that generate post-zygotic or ecological incompatibilities among them (Coyne & Orr 2004). For example, interactions with heterospecifics may often also involve competitive interactions for resources, so that reproductive and ecological character displacement may act in tandem to generate population divergence among conspecifics (Boughman et al. 2005; Pfennig & Pfennig 2005).
Although networks from all three populations in our study tended to prefer local calls, networks from a given population did not necessarily show the same level of discrimination against different types of foreign calls (figure 2). Such a finding indicates that the evolution of discrimination against heterospecifics does not necessarily result in the rejection (or equal treatment) of all foreign calls. Discrimination against foreign calls tended to be weaker when local and foreign calls were more similar (table 3). Indeed, calls from the A and AC populations were the most similar (figure 1) and networks from both populations were less discriminating against calls from the alternate population than they were against calls from the AB population. Similarly, when tested for their preferences of local calls versus calls from alternative replicates of their same population type, the preference for local calls was weakest in the A population (figure 2; see also table 2), which exhibited very low variation in calls across replicates (i.e. local calls and foreign calls were all similar; figure 1). By contrast, the preference for local calls versus calls from alternative replicates was highest in the AB population (figure 2; see also table 2), which exhibited higher variation in calls across replicates (figure 1). These results suggest that different types of heterospecific interactions may be more likely to contribute to reproductive isolation if they promote the evolution of opposing signal characters among conspecific populations. Thus, the particular mating behaviours that evolve in response to heterospecifics may determine whether populations become reproductively isolated.
One feature of our simulations that undoubtedly promoted the diversification of mating behaviours among the conspecific populations was the close coevolution between signals and receivers. Such a pattern of coevolution is often likely between males and females (Andersson 1994). If, however, signal evolution (or receiver perception) is under direct countervailing selective pressures (e.g. from predators or energetic or physiological limitations) or affected indirectly by the evolution of correlated characters (pleiotropy), divergence among populations may in turn be limited. Predicting the circumstances under which reproductive character displacement may promote the evolutionary diversification of mating behaviours and possibly speciation among conspecific populations may therefore require a comprehensive understanding of the selective and pleiotropic factors that determine the evolution of mating behaviours within and among populations.
One factor not included in our model that can dramatically affect the degree to which populations diverge is gene flow. In our model, the populations were evolving in isolation, which facilitated their divergence. Gene flow among populations can reduce the likelihood of divergence, however, by introducing trait and preference alleles from one population into others. If migration rates are sufficiently high and if alleles introduced via gene flow spread in a population, differences among conspecific populations for mating behaviours could disappear. Yet, although gene flow typically reduces divergence, it need not eliminate divergence especially if selection is strong (Liou & Price 1994; Kelly & Noor 1996; Kirkpatrick & Servedio 1999). Moreover, our findings suggest that once populations begin to diverge in mating behaviours, migrant males or females would be at a selective disadvantage because they would be less likely to mate than resident individuals (table 2; figure 2). Consequently, as long as gene flow does not eliminate initial differentiation of mating behaviours among populations, their divergence could counteract the effects of gene flow and thereby further enhance the likelihood that populations become reproductively isolated.
Reproductive character displacement is generally viewed as a result of reinforcement and the final stages of speciation (Dobzhansky 1940; Howard 1993; Coyne & Orr 2004) or a consequence of interactions that accentuate existing species boundaries (Butlin 1987). Our results suggest that reproductive character displacement can potentially initiate speciation. Such a process has recently been described, e.g. in the green-eyed tree-frog, Litoria genimaculata (Hoskin et al. 2005). Because most species co-occur with heterospecifics and probably with different heterospecifics in different parts of their range, these results further suggest that reproductive character displacement could potentially initiate ‘speciation cascades’—multiple speciation events across a given species' range. Yet, whether reproductive character displacement often generates diversity in this way remains an open question. Discovering the role that reproductive interactions between species plays in rapid evolutionary diversification is therefore potentially critical for assessing how mate choice contributes to the speciation process.
Acknowledgments
We are grateful to D. Pfennig, H. Farris, P. Hurd, C. Smith, J. Nelson, Y. Zhang, T. Feldman, R. Bartlett, the M. Ryan and M. Kirkpatrick lab groups and two anonymous reviewers for discussion and comments on this work. This work was funded by postdoctoral fellowships and a grant to K.P. from the National Science Foundation and the National Institutes of Health funded SPIRE program.
References
- Andersson M. Princeton University Press; Princeton, NJ: 1994. Sexual selection. [Google Scholar]
- Boughman J.W, Rundle H.D, Schluter D. Parallel evolution of sexual isolation in sticklebacks. Evolution. 2005;59:361–373. [PubMed] [Google Scholar]
- Butlin R. Speciation by reinforcement. Trends Ecol. Evol. 1987;2:8–13. doi: 10.1016/0169-5347(87)90193-5. 10.1016/0169-5347(87)90193-5 [DOI] [PubMed] [Google Scholar]
- Coyne J.A, Orr H.A. Sinauer Associates; Sunderland, MA: 2004. Speciation. [Google Scholar]
- Demuth H, Beale M. The Math Works; Natick, MA: 1997. Neural network toolbox. [Google Scholar]
- Dobzhansky T. Speciation as a stage in evolutionary divergence. Am. Nat. 1940;74:312–321. 10.1086/280899 [Google Scholar]
- Elman J.L. Finding structure in time. Cogn. Sci. 1990;14:179–211. 10.1016/0364-0213(90)90002-E [Google Scholar]
- Enquist M, Ghirlanda S. Princeton University Press; Princeton, NJ: 2005. Neural networks and animal behavior. [Google Scholar]
- Gabor C.R, Ryan M.J. Geographical variation in reproductive character displacement in mate choice by male sailfin mollies. Proc. R. Soc. B. 2001;268:1063–1070. doi: 10.1098/rspb.2001.1626. 10.1098/rspb.2001.1626 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gerhardt H.C. Sound pattern-recognition in some North American treefrogs (Anura, Hylidae)—implications for mate choice. Am. Zool. 1982;22:581–595. [Google Scholar]
- Gerhardt H.C. Reproductive character displacement of female mate choice in the gray treefrog Hyla chrysoscelis. Anim. Behav. 1994;47:959–969. 10.1006/anbe.1994.1127 [Google Scholar]
- Gerhardt H.C, Huber F. University of Chicago Press; Chicago, IL: 2002. Acoustic communication in insects and anurans: common problems and diverse solutions. [Google Scholar]
- Hoskin C.J, Higgie M, McDonald K.R, Moritz C. Reinforcement drives rapid allopatric speciation. Nature. 2005;437:1353–1356. doi: 10.1038/nature04004. 10.1038/nature04004 [DOI] [PubMed] [Google Scholar]
- Howard D.J. Reinforcement: origin, dynamics and fate of an evolutionary hypothesis. In: Harrison R.G, editor. Hybrid zones and the evolutionary process. Oxford University Press; New York, NY: 1993. pp. 46–69. [Google Scholar]
- Höbel G, Gerhardt H.C. Reproductive character displacement in the acoustic communication system of green tree frogs (Hyla cinerea) Evolution. 2003;57:894–904. doi: 10.1111/j.0014-3820.2003.tb00300.x. [DOI] [PubMed] [Google Scholar]
- Kelly J.K, Noor M.A.F. Speciation by reinforcement: a model derived from studies of Drosophila. Genetics. 1996;143:1485–1497. doi: 10.1093/genetics/143.3.1485. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kirkpatrick M, Servedio M.R. The reinforcement of mating preferences on an island. Genetics. 1999;151:865–884. doi: 10.1093/genetics/151.2.865. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lande R. Models of speciation by sexual selection on polygenic traits. Proc. Natl Acad. Sci. USA. 1981;78:3721–3725. doi: 10.1073/pnas.78.6.3721. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liou L.W, Price T.D. Speciation by reinforcement of premating isolation. Evolution. 1994;48:1451–1459. doi: 10.1111/j.1558-5646.1994.tb02187.x. [DOI] [PubMed] [Google Scholar]
- Noor M.A. Speciation driven by natural selection in Drosophila. Nature. 1995;375:674–675. doi: 10.1038/375674a0. 10.1038/375674a0 [DOI] [PubMed] [Google Scholar]
- Pfennig K.S. The evolution of mate choice and the potential for conflict between species and mate-quality recognition. Proc. R. Soc. B. 1998;265:1743–1748. 10.1098/rspb.1998.0497 [Google Scholar]
- Pfennig K.S. Female spadefoot toads compromise on mate quality to ensure conspecific matings. Behav. Ecol. 2000;11:220–227. 10.1093/beheco/11.2.220 [Google Scholar]
- Pfennig K.S, Pfennig D.W. Character displacement as the ‘best of a bad situation’: fitness trade-offs resulting from selection to minimize resource and mate competition. Evolution. 2005;59:2200–2208. [PubMed] [Google Scholar]
- Pfennig, K. S. & Ryan, M. J. In press. Character displacement and the evolution of mate choice: an artificial neural network approach. Phil. Trans. R. Soc. B [DOI] [PMC free article] [PubMed]
- Phelps S.M, Ryan M.J. Neural networks predict response biases of female túngara frogs. Proc. R. Soc. B. 1998;265:279–285. doi: 10.1098/rspb.1998.0293. 10.1098/rspb.1998.0293 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Phelps S.M, Ryan M.J. History influences signal recognition: neural network models of túngara frogs. Proc. R. Soc. B. 2000;267:1633–1639. doi: 10.1098/rspb.2000.1189. 10.1098/rspb.2000.1189 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Phelps S.M, Ryan M.J, Rand A.S. Vestigial preference functions in neural networks and túngara frogs. Proc. Natl Acad. Sci. USA. 2001;98:13 161–13 166. doi: 10.1073/pnas.231296998. 10.1073/pnas.231296998 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ryan M.J, Getz W. Signal decoding and receiver evolution—an analysis using an artificial neural network. Brain Behav. Evol. 2000;56:45–62. doi: 10.1159/000006677. 10.1159/000006677 [DOI] [PubMed] [Google Scholar]
- Ryan M.J, Rand A.S. Species recognition and sexual selection as a unitary problem in animal communication. Evolution. 1993;47:647–657. doi: 10.1111/j.1558-5646.1993.tb02118.x. [DOI] [PubMed] [Google Scholar]
- Saetre G.P, Moum T, Bures S, Kral M, Adamjan M, Moreno J. A sexually selected character displacement in flycatchers reinforces premating isolation. Nature. 1997;387:589–592. 10.1038/42451 [Google Scholar]
- Servedio M.R, Noor M.A.F. The role of reinforcement in speciation: theory and data. Annu. Rev. Ecol. Evol. Syst. 2003;34:339–364. 10.1146/annurev.ecolsys.34.011802.132412 [Google Scholar]
- Sokal R.R, Rohlf F.J. W.H. Freeman and Co; New York, NY: 1995. Biometry. [Google Scholar]
- Spencer H.G, McArdle B.H, Lambert D.M. A theoretical investigation of speciation by reinforcement. Am. Nat. 1986;128:241–262. 10.1086/284557 [Google Scholar]