Explaining the explosion: modelling hybrid invasions

Abstract

The emergence of hybrids between native and introduced species is an increasingly widespread problem which can alter entire ecosystems. We present a general model for the hybridization of two plant species to investigate the conditions under which hybrid invasions can occur, and the ecological and genetic consequences of such hybridizations. We find that parental compatibility and fecundity are important determinants of whether (and at what rate) hybrid genotypes emerge. Enhanced hybrid fitness traits affect both the population's genetic structure and total rate of increase, with rapid selection for the fittest genotype. Conversely, if different genotypes maximize different life-history characteristics, the ensuing population can be genetically very variable. The model provides a novel approach to evaluate the contributions of population dynamic and genetic processes in the study of hybrid invasions.

1. Introduction

An alien species introduced into a new range is often phenomenally successful: this may be due to exploitation of a previously unfilled niche (Williamson 1996), a release from its natural predators or diseases (Callaway et al. 2004), or increased competitive ability relative to the native biota (Holway 1999). Successful invaders often have a detrimental effect on local biodiversity, and attempts to control or reverse their spread can be notoriously difficult and costly (Pimentel et al. 2000). In many ecosystems, one of the greatest threats to endemic species comes not from the alien itself, but from the emergence of hybrids between the native and alien (Ellstrand & Schierenbeck 2000). This can lead to the loss of native genotypes through interbreeding or ecological displacement via the emergence of highly fit hybrid genotypes (Rieseberg et al. 1999).

A particular example of this is the invasion of hybrid cordgrass (Spartina foliosa×alterniflora) in the tidal salt marshes of San Francisco Bay. The native S. foliosa is relatively slow-growing, has low seed-set and is limited to higher tidal elevations (D. R. Ayres, unpublished data). Since the introduction of the Atlantic cordgrass S. alterniflora in the 1970s, highly fit hybrids have emerged, whose growth rates, fecundity and tolerance to environmental conditions exceed both parental lineages (Ayres 2003). The hybrids are detrimental to many organisms in the Bay by overgrowing open mudflats, which are crucial foraging areas for migrant and wintering shorebirds, and by accumulating sediment in their root mass (thus changing the tidal height). Over the last 30 years, the area covered by hybrid cordgrass has increased faster than exponentially (Ayres et al. 2004). If this invasion continues unchecked, it seems likely that the native foliosa is faced with extinction (Ayres 2003).

In order to assess the risk of a native–exotic hybridization occurring, and to design effective control strategies for existing hybrid invasions, it is vital to determine the ecological and genetic factors which drive the emergence, and subsequent invasion of hybrid genotypes. Mathematical models are a useful tool for investigating the relative importance of these mechanisms. In comparison to the wealth of publications on models for the replacement of a native species by an exotic invader, relatively little attention has been paid to modelling native–exotic hybridizations. Models by Huxel (1999), Epifanio & Philipp (2001) and Ferdy & Austerlitz (2002) focus on the genetic aspects of hybridization by examining changes in the relative frequency of genotypes, without explicit attention to the population dynamics. Conversely, Wolf et al. (2001) present a model incorporating more details of the life history, under the assumption that all hybrids are equally fit. There is therefore a need for models which incorporate the ecological and genetic aspects of hybridization, in order to address questions of both population spread and genetic composition.

In this paper, we present a simple integro-difference equation model to describe the population dynamics and genetics of two hybridizing plant species invading an open niche. It is therefore directly applicable to the invasion of San Francisco Bay by hybrid cordgrass, and more generally to hybridization where two previously isolated plant species come into contact through human introduction (e.g. cultivated and wild sunflowers; Ellstrand & Schierenbeck 2000) or natural range expansion (e.g. oaks; Petit et al. 2003). We find that even in the absence of any fitness advantage, hybrid genotypes are able to emerge provided there is sufficient compatibility between the parental genotypes. Enhanced hybrid fitness traits affect both the population's genetic structure and total rate of increase, dependent on the height and location in genotype space of the trait's maximum value. When one hybrid genotype is significantly fitter than all others, the native and exotic both decrease in frequency and the population is rapidly dominated by the fittest genotype. Conversely, if different traits attain their maxima at different genotypes, the resulting population may be genetically very variable. The implications of these results for predicting the emergence of hybrids, and for the control of hybrid invasions, is briefly discussed.

2. Model

Here, we derive a model to examine how the genetic structure of, and total area occupied by the population changes through time when the life history of each plant is a function of its genotype. Since our goal is to elucidate the roles of genetic structure and phenotypic fitness on the population dynamics, we make the simplifying assumptions of spatial homogeneity and no age structure (i.e. juveniles become adults after one generation). We further assume that there are no density-dependent effects: this is plausible in describing the early stages of an invasion into naive habitat (through, for example, a natural range expansion or colonization following a disturbance event).

We adopt a simple quantitative genetics approach to model sexual reproduction. In the spirit of previous quantitative genetic models (Bulmer 1980; Doebeli 1996), we assume that a large number of loci are acting additively to determine an individual's phenotype. Since this approach does not keep track of individual alleles, it is unsuitable for examining explicitly the effects of more complex phenomena such as epistasis and recombination; however, we believe this is more than compensated for by the resulting conceptual clarity. Under this assumption, an individual's phenotype can be represented by a continuous variable x, scaled so that the native genotype has value x=−1, and the genotype of the alien is x=+1.

The key variable in this model is the area occupied by individuals of genotype x in generation t (denoted P_t(x)). The area occupied by plants in a new season is the sum of contributions from vegetative growth and survival of adult plants, and seedling recruitment. The model takes the form

$$P_{t+1}(x)=R(x)P_t(x)+A(x){\int }_y{\int }_{z}M(x,y,z)\text{d}y\text{d}z,$$ 2.1

where R(x) is the annual net vegetative growth rate of plants of genotype x, and A(x) is the seedling vigour (the average area occupied by a seedling of type x). The term M(x, y, z) represents the number of seeds of type x produced from male parents of type y and female parents of type z, so that the double integral gives the total number of seeds produced of type x. M is the product of the frequency of pollen produced by parents of genotype y, the number of ovules from parents of type z, the probability that pollen reaches an ovule (β, assumed constant) and the probability of each resulting gamete combination producing a seed of genotype x. This is expressed mathematically by

$$M(x,y,z)=\beta \frac{N_m(y)P_t(y)}{{\int }_s{N}_m(s)P_t(s)\text{d}s}{N}_f(z)P_t(z)\alpha (y,z){\int }_w\theta (w,y)\theta (x-w,z)\text{d}w,$$ 2.2

where N_m(x) and N_f(x) are, respectively, the number of pollen grains and ovules produced by parent x, and α(y, z) is the compatibility of parents y and z (i.e. the probability that a pollen–ovule encounter results in viable seed production). The term θ(a, b) gives the probability of producing a gamete of type a from a parent of genotype b, and is assumed to be normally distributed with mean b/2 and variance σ²(b). The variance in gamete production is a normally distributed function of the parental genotype; hybrids with genotype x=0 produce the widest variation in gametes (σ²(0)=0.25), while the gamete variation in each parental species is assumed to be low (σ²(±1)=0.0025).

3. Material and methods

The model described by equations (2.1) and (2.2) was solved numerically in FORTRAN over 50 generations, using a formula of fourth-order accuracy to approximate each integral (Press et al. 1992), under varying assumptions of compatibility between genotypes and the functional dependence of life-history traits on genotype. The population size and genetic structure were measured by recording the total area occupied by plants of all genotypes,

$$P_t={\int }_x{P}_t(x)\text{d}x,$$ 3.1

and the relative frequency of each genotype in the population,

$$q_t(x)=\frac{P_t(x)}{P_t}.$$ 3.2

The results are compared to those from a ‘null model’ in which all genotypes are equally compatible (i.e. α=1.0) and have equal fitness (F(x)=F, F=R, A, N_m, N_f). When compatibility is not constant, it is assumed to decline linearly with the genetic distance of the parents (i.e. $\alpha (y,z)=1-0.5|y-z|$ for $|y-z|<2$; 0 otherwise). When the life-history traits (growth, pollen and ovule production, seedling vigour) are not assumed equal for all genotypes, they are distributed normally. The trait value for the native is fixed, leaving the height and location of the maximum as the two free parameters. Thus, the functional dependence of each trait on genotype can be written in the form

$$F(x)=F(1+\mathrm{\Delta }F)\text{exp}\left(-\frac{{(x-{\mu }_F)}^2}{2{\sigma }_F^2}\right),$$ 3.3

where ΔF is the proportionate difference between the maximum trait value and the trait value of the native (F), and the variance is fixed by the condition F(−1)=F.

We are able to reduce the number of parameters in the model by defining the aggregate parameter $S=\beta A{N}_f$, which represents the fecundity, or area of seedlings produced by a unit area of the native. The relative sizes of the native's growth (R) and fecundity (S) rates are a measure of the relative importance of sexual versus asexual processes for population expansion. The results are shown for two parameter sets for the native: one where the plant grows primarily vegetatively (R=1.05) and seedling production is relatively low (S=0.1 or 0.01), the other whereby the population is maintained primarily by reproduction (R=0.6, S=0.5). Unless otherwise stated, all simulations are started with the initial population consisting of 99% native and 1% exotic.

4. Results

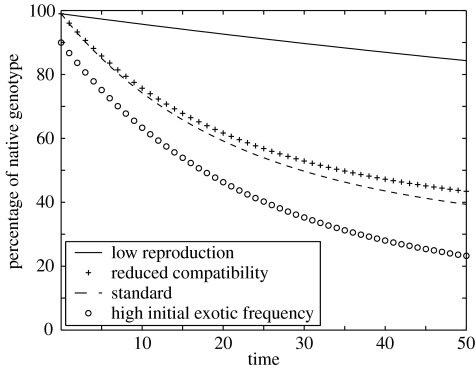
The model was run under a ‘null’ scenario, whereby all genotypes are equally fit (figure 1). Even in the absence of a selective advantage to hybrid genotypes, the relative frequency of the native declines through hybridization (and the frequency of the exotic undergoes a similar decline). How rapidly the native decreases in frequency depends strongly on the fecundity of the population, the initial ratio of native and exotic genotypes and the relative compatibility of different genotypes.

Figure 1.

Decline in the relative frequency of the native genotype in a neutrally selective environment (i.e. all genotypes are equally fit). The default parameter values (dashed line) for vegetative growth rate and fecundity are, respectively, R=1.05 and S=0.1. The initial population consists of 99% native and 1% exotic genotypes, and all genotypes are assumed equally compatible. The following deviations from the standard are considered: reduced seedling production (bold line, S=0.01), reduced compatibility (pluses, $\alpha (y,z)=1-0.5|y-z|$ for $|y-z|<2$; 0 otherwise) and reduced initial frequency of the native (circles, 90% native and 10% exotic).

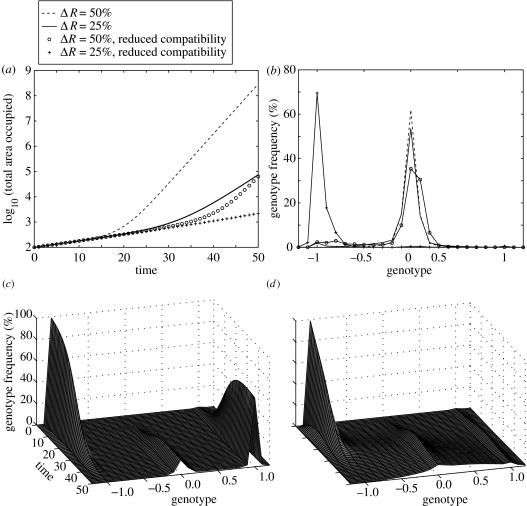
When a life-history trait of a plant is a function of its genotype, the effects on both the population growth rate (figure 2a) and genetic structure (figure 2b) can be dramatic. Most notably, an apparent accelerating population growth rate may be observed (figure 2a). In the case where hybrids exhibit an elevated growth rate relative to the native, the fastest-growing genotype increases rapidly in frequency within the population. This results in an increase in the frequency of pollen and ovules produced by this genotype, which in turn results in higher production of seedlings with this genotype. The net population growth rate therefore increases to approach that of a population consisting entirely of the fittest genotype. The results illustrated here are for elevated vegetative growth rate of hybrids, but sufficiently large changes in seedling vigour and ovule production can also result in faster-than exponential population growth.

Figure 2.

Effect of elevated hybrid vegetative growth rate on (a) the total population growth rate and (b) the genetic structure of the population after 50 generations. The growth rate is varied by changing the proportional difference between the growth rate of the native and that of the fittest genotype (ΔR). The results are shown for two values of ΔR, when all genotypes are equally compatible (bold and dashed lines), and when compatibility is a function of the genetic distance of the parents (pluses and circles). The maximum growth rate occurs for individuals with genotype x=0; fecundity is low (S=0.01), and the remaining parameters are as for the default case in figure 1. (c, d) Effect of shifting the location of the fastest-growing genotype to x=0.5 on the genetic structure of the population (here ΔR=0.25). The results are shown when fecundity is (c) low (S=0.01) and (d) high (S=0.1).

The addition of compatibility constraints can delay, or even prevent, the invasion of novel genotypes. If hybridization does eventually occur, the invasion continues at the same rate as if all genotypes were equally compatible (figure 2a, cf. dashed and circled lines). Thus, reduced compatibility between genetically distant congeners may help to explain the ‘lag-time’ observed between the introduction of an exotic and the subsequent appearance of hybrids.

The location of the fitness maximum in genotype space strongly influences the resulting genetic structure of the population. In the above example, the fittest genotype is also the most commonly produced genotype in F₁ hybrids, and hence this genotype rapidly dominates the population. When the location of the maximum is skewed, such that it is unlikely to appear in the initial round of hybridization (figures 2c,d), the fittest genotype takes longer to emerge, and may not become the dominant genotype within an ecologically relevant timescale. When fecundity is low (figure 2c), relatively little hybridization occurs over the first 50 generations. The exotic becomes the dominant genotype (since in this case it is fitter than the native) even though it is not the fittest possible genotype. Some F₁ hybrids eventually appear, but further introgression does not occur within this time-frame. When fecundity is increased by an order of magnitude (figure 2d), there is a noticeable shift in the population structure towards the fittest genotype, although the population remains genetically very variable.

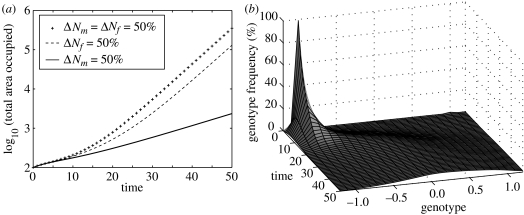
In reality, we might expect certain life-history traits to be genetically linked. For example, average inflorescence length varies with genotype in Spartina, resulting in more pollen and ovule production per unit area for those genotypes with large inflorescences. In this model, elevated hybrid pollen production alone does not affect the rate of population increase, since the number of seeds produced is assumed proportional to the number of ovules (it does, however, strongly influence the genetic structure of the population). Elevated ovule production can result in accelerating population growth (figure 3a, dashed line), but when both pollen and ovule production are genetically correlated (pluses), the ensuing population growth rate is considerably more rapid as the two mechanisms feed back on each other to select for the fittest genotype.

Figure 3.

(a) Effect of elevated hybrid life-history traits on population growth when two traits (pollen production, N_m and ovule production, N_f) are genetically linked. The default vegetative growth and fecundity parameters are R=0.6 and S=0.5. When pollen production (bold line), ovule production (dashed line) or both (pluses) are functions of genotype, their maximum occurs at genotype x=0, and is 50% larger than that of the native $(\Delta N_m,\Delta N_f=50\%)$. (b) Evolution of the population genetic structure when two of the life-history traits have maxima at different genotypes. Here, the maximum vegetative growth rate occurs for genotype x=0, and is 25% larger than the native's (ΔR=25%), while the maximum seedling vigour occurs for genotype x=0.5, and is 50% larger than the native's (ΔA=50%).

When two elevated fitness traits attain their maxima at different genotypes (through, for example, a trade-off between resources allocated to vegetative growth and reproduction), more interesting dynamics can ensue (figure 3b). If one of the elevated life-history traits has a stronger effect on population growth than the others, the population will tend to converge on that genotype (not shown). However, when two opposing life-history traits have similar effects on population growth, a wide range of phenotypically distinct genotypes can persist over many generations (figure 3b). Such trade-offs between genotypes may help to explain the existence of ‘hybrid swarms’, whereby hybrids with very different life-history characteristics appear to coexist.

5. Discussion

Interactions between ecological and evolutionary processes play an integral part in many contemporary biological invasions (Lambrinos 2004). Using a novel discrete-time model, we have highlighted the importance of the interplay between population dynamic and genetic factors in determining the outcome of hybridization between native and exotic species. Under varying assumptions about reproductive compatibility among genotypes, and the functional dependence of life-history traits on genotype, a wide range of outcomes is possible, including no hybridization, replacement of the native by the exotic, rapid selection for the fittest genotype and an increase in the overall genetic diversity among hybrids. The model suggests potential mechanisms for phenomena observed in the invasive population of hybrid cordgrass (Spartina spp.) in San Francisco Bay, including the apparent faster-than exponential population growth rate, a lag-time between the introduction of the exotic and the appearance of the first hybrids and the existence of a hybrid swarm of phenotypically distinct individuals.

In agreement with our findings, previous models of hybridization between native and exotic taxa (Huxel 1999; Epifanio & Philipp 2001; Wolf et al. 2001) concur that displacement of the native by hybrids can occur very rapidly (within tens of generations), but that sufficiently strong compatibility constraints can allow the native to persist (Ferdy & Austerlitz 2002). However, the model presented here makes some important conceptual advances. By considering a large number of genotypes and the interaction of several life-history traits, the model is able to make predictions relating to the rate of expansion and the genetic structure of the resulting population. Such predictions are impossible from models which consider only three population states (native, exotic and hybrid, cf. Huxel 1999; Wolf et al. 2001), or which subsume many population processes into a single selection coefficient without an explicit representation of the dynamics (Epifanio & Philipp 2001; Ferdy & Austerlitz 2002).

The model allows us to make predictions on the likelihood of the emergence of hybrid genotypes and could be of use in the design of effective control strategies for specific hybrid invasions. For species pairs with naturally low fecundity, or compatibility constraints (for example, different flowering times or different numbers of chromosomes), hybridization is less likely to occur, and if it does so, will progress at a relatively slow rate. Conversely, relatively compatible species (for example, those which diverged more recently in evolutionary time) with high reproductive success will be most vulnerable to hybridization. The rate of invasion of hybrid genotypes will depend on the functional dependence of the life-history traits on genotype: the most rapid invasion will occur if some hybrid genotypes are substantially fitter than the native, if these genotypes occur in the first round of hybridization, and if there are highly fit genotypes which maximize two or more life-history traits. Removal of exotic species and hybrid genotypes soon after detection is advisable, even if these genotypes do not appear to initially exhibit invasive spread.

The model framework is amenable to the addition of more complex factors such as spatial structure and density dependence. In a spatially heterogeneous landscape, local variation in recruitment and environmental conditions could promote local selection for different genotypes, and could perhaps provide a refuge for native genotypes from hybridization. Propagule pressure and the range of pollen and seed dispersal will also have important effects on the maintenance of local genetic structure. Density-dependent processes may have an effect at both the early and latter stages of an invasion. Pollen limitation in isolated plants can cause an Allee effect (Davis et al. 2004), which could slow or even prevent the invasion of hybrid genotypes. In a crowded, resource-limited environment, a different set of traits is likely to be selected for than at the front of the invasion, which may also act to promote genetic heterogeneity within the population. The incorporation of such complexities will form the basis of future work.