Lifetime reproductive success and density-dependent, multi-variable resource selection

Abstract

Individuals are predicted to maximize lifetime reproductive success (LRS) through selective use of resources; however, a wide range of ecological and social processes may prevent individuals from always using the highest-quality resources available. Resource selection functions (RSFs) estimate the relative amount of time an individual spends using a resource as a function of the proportional availability of that resource. We quantified the association between LRS and coefficients of individual-based RSFs describing lifetime resource selection for 267 female red deer (Cervus elaphus) of the Isle of Rum, Scotland, from 1970 to 2001. LRS was significantly related to first- and second-order effects of selection for Agrostis/Festuca grassland and proximity to the sea coast (quality of forage within Agrostis/Festuca grassland was highest nearest the coast (ratio of short : long grassland)). The benefits of selecting for quality in Agrostis/Festuca grassland, however, traded-off with increases in LRS gained by avoiding conspecific density. LRS was inversely associated with local density, which was highest along the coast, and reproductive benefits of selecting Agrostis/Festuca grassland diminished with increasing density. We discuss the relevance of these results to our understanding of the spatial distribution of red deer abundance, and potential applications of our approach to evolutionary and applied ecology.

1. Introduction

In a seminal paper on the concept of niche, Roughgarden (1972) maintained that niche breadth and position are subject to natural selection. This observation underscores a fundamental concept in animal ecology: patterns in the spatial distribution of abundance result from individual attempts to maximize fitness through selective use of habitat resources. Roughgarden understood the niche to be a hypervolume described, in part, by a range of resources modified by associated abiotic and biotic covariates (Hutchinson 1965); however, most research into the link between fitness and resource selection has focused on an individual's use of a single resource variable, such as a type of nest site or habitat (Fretwell & Lucas 1970, reviews in Rosenzweig 1981, 1991; Morris 2003). Few studies have demonstrated links between fitness and resource selection when individuals use more than one habitat resource (e.g. McLoughlin et al. 2005; Pettorelli et al. 2005).

Selection for multiple resources and modifying covariates can be quantified for individuals using functions that are proportional to the probability of use (i.e. resource selection functions (RSFs); Manly et al. 2002). We propose to relate an organism's lifetime reproductive success (LRS) to coefficients describing its lifetime RSF, and abiotic and biotic covariates that might interact with effects of resource selection on LRS. Linking LRS to multi-variable resource selection will enable us to identify habitat resources critical to the survival and reproduction of species, but also pressures acting on resource selection in the broader context of a species' realized niche. For example, model interaction terms may identify fitness trade-offs between selection for quality within a heterogeneous resource type and disadvantages presented by competition or predation risk.

Here, using RSFs, we quantify lifetime resource selection for female red deer on the Isle of Rum, Scotland. Using Poisson regression, we then relate LRS of hinds to RSF coefficients describing their selection for habitat resources and covariates that modify the relationship between resource selection and LRS. Our approach enables us to observe an ecological trade-off between advantages resulting from a hind's selection for quality within a grassland community and disadvantages presented by higher conspecific density.

2. Material and methods

(a) Study area and sampling

We collected data in a 14 km² study area on the Isle of Rum, Scotland (57°01′ N, 06° 17′ W, NM-402996), from 1970 to 2001. The northern boundary of the study area followed approximately 3.5 km of coastline from Kilmory Bay to Rubha Shamhnan Insir. Movements of hinds were largely contained along the seashore and a 4.0 km section of the Kilmory River (Kilmory Glen), which drains the surrounding hills (elevation approx. 300 m) and empties into Kilmory Bay. We classified vegetation into five main types following Clutton-Brock et al. (1982). Grassland dominated by Agrostis and Festuca spp. (‘Agrostis/Festuca grassland’) occurred near the coast at Kilmory Bay and Shamhnan Insir, and along Kilmory Glen. The community was composed of two sub-types (combined for analysis): G1 grassland (‘short greens’) occurred in well-drained soils and calcareous dunes with relatively high pH, and G2 grassland (‘long greens’), generally used later in the season after most of the standing crop of G1 grassland was removed (Clutton-Brock et al. 1982, 1987), occurred in more acidic soil along edges of streams and the Kilmory River (Upper and Lower Glen). Although G2 grassland presented hinds with a larger standing crop compared to G1 grassland, long greens contained a substantial proportion of dead grass that made it more difficult for deer to forage selectively; further, long greens offered relatively lower digestibility due to increased cellulose and lignin levels (Clutton-Brock et al. 1982, p. 23). Other communities in the study area, supporting lower quality forage compared to G1/G2 grasslands (Clutton-Brock et al. 1982, 1987), included Juncus-dominated marshland along the Kilmory River and expanses of Molinia-dominated flush and Calluna-dominated heath and heather moorland in the glen and surrounding hills. Eriophorum-dominated bog (blanket bog) occurred in small patches throughout the area.

The study area supported between 200 and 400 red deer (50–200 hinds) in a natural state (free range, unculled since 1972). Through regular, ground-based censuses (47±2.6 censuses per year (mean±s.d.)), we compiled movements (341±208 sightings per hind) and complete life histories (from birth to death) for 270 uniquely marked hinds (we only use the female component of the population) that lived to at least 3 years of age, which was the shortest lifespan for which non-zero LRS was observed. Clutton-Brock et al. (1982) provides a detailed description of the deer population and our sampling protocol.

(b) Multi-variable resource selection

An RSF is calculated by comparing the known distribution of resource use by an animal with that expected from a random distribution. At the landscape level, locations selected by animals (e.g. points in space or ‘pixels’ of land) may be conceived as resource units, described by ‘resource variables’ (e.g. patch or habitat type) or modifying covariates (e.g. elevation, slope, distance to water). Resource selection is defined as the use of a resource unit in amounts greater than what is proportionately available.

Several techniques are available to estimate RSFs (Manly et al. 2002). A common approach (applied here) uses binary logistic regression to estimate coefficients (β_j) for a vector of k predictor resource variables or covariates associated with resource units (sites). Sites where an individual is present are coded 1, whereas a random sample (or all possible sites) is coded 0. Note that in our application, logistic regression is used as an estimating function and not for statistical inference (Boyce et al. 2002, p. 282).

We compiled census observations of hinds into 100×100 m census blocks (resource units) within the study area. Attributes of census blocks included proportions of the main vegetation types occurring on Rum. Hinds forage on seaweed (Clutton-Brock et al. 1982, p. 231), so we calculated the distance (m) from the centre of a block to the intertidal zone and included this as a resource. Distance to the coast can also be viewed as a modifier of Agrostis/Festuca grassland, capturing heterogeneity (e.g. ratio of G1 : G2 grassland) within the resource due to associated gradients in elevation, soil composition and nutrient availability (including the extent to which the presence of sea gull colonies along the coast increased soil nitrogen and phosphorus, and vegetation nitrogen content (Iason et al. 1986)). The ratio of G1 : G2 grasslands within resource units (ha) containing Agrostis/Festuca was inversely related to distance to the coast (<1 km, 4.2±0.77 (mean ratio±s.e.m.); >1 km, 0.94±0.22; t₃₈₇=3.78, p<0.0002). To better reflect nonlinear changes within Agrostis/Festuca grassland associated with proximity to the seashore, we incorporated distance to the coast as a squared term for analysis. We did not consider additional abiotic covariates that we knew to be correlated with occurrence of vegetation types or proximity to the coast (e.g. elevation; Clutton-Brock et al. 1982, p. 314).

For each hind, we estimated a lifetime RSF using logistic regression (SPSS v. 13.0, SPSS Inc., Chicago, IL, USA). We defined use of resource units from sightings at census blocks and availability of resource units from a random sample of the totality of census blocks where hinds were observed to occur (1377 blocks (ha)). For all hinds, we used a 1 : 5 ratio of used : available resource units to estimate RSFs (individual-based RSFs are only comparable if the same ratio of used : available resource units is employed in the estimating function). Proportional availability of resource types stabilized after randomly sampling approximately 100 resource units (e.g. estimated proportional availability of Agrostis/Festuca grassland did not differ after sampling 100 versus 1000 times (t₁₀₉₈=0.036, p=0.97), nor did variance in grassland availability (Levene's test, F_1,1098=0.19, p=0.67)). Because home ranges of hinds (95% fixed kernel) ranged as high as 1098 ha, our scale of study best corresponded to that of third-order resource selection (Johnson 1980). In specifying equal availability of resource units for all hinds we did not consider individual variation in functional responses in habitat use (Mysterud & Ims 1998). By not constraining availabilities of resource units to a hind's home range, interpretation of the strength of individual-based resource selection remained comparable among hinds; however, in our application, this probably reduced effect size in the relationship between LRS and resource selection.

In addition to developing individual-based RSFs, we computed an individual-pooled RSF to describe the average resource selection pattern adopted by hinds. Population mean β coefficients were estimated using logistic regression from a sample of locations of use (maximum 100 randomly selected locations per hind) contrasted with a sample of random locations five times the size of the pooled sample of locations of use.

(c) LRS and Poisson regression

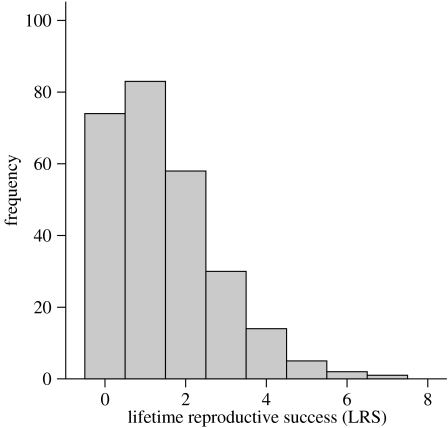
We used LRS to measure fitness of hinds. LRS is a valid, single-generation proxy of long-term genetic contribution (Brommer et al. 2004). We calculated LRS as the number of female calves to which hinds gave birth and which survived to an age of 1 year or more (i.e. age of independence). Because LRS was measured in counts and did not greatly differ from a Poisson distribution (${\chi }_{3(\text{adj})}^2=6.13$, p=0.11; figure 1), we fitted a Poisson regression model (McCullagh & Nelder 1989) to quantify the influence of multi-variable resource selection on individual performance. LRS was the response variable, and predictors included β coefficients describing lifetime resource selection (from individual-based RSFs) and the interaction β_{Agrostis/Festuca}×β_distcoast². To consider effects of density-dependence in habitat selection (Fretwell & Lucas 1970; Rosenzweig 1981, 1991; Morris 2003), we included in our model the interaction between a hind's selection for Agrostis/Festuca grassland and local density experienced by hinds. We defined local density of an individual as the total number of hinds aged 1 year or more within the coarse-scale, sub-population cluster to which an individual belonged, determined from spatial hierarchical cluster analysis (‘scalar 90’ of Coulson et al. 1997). Units were not individuals per hectare; however, local density is still an appropriate term because clustering relied on the proximity of individuals to one another (Coulson et al. 1997). Average local density experienced by a hind over its lifetime varied considerably among individuals (72.3±25.4 hinds (mean±s.d.), range 2.0–108.5). Variance in local density (i.e. year-to-year variation) also differed among hinds, and we included in our regression the interaction between variance in local density and selection for Agrostis/Festuca grassland. First-order terms of local density and variance in local density were included during model selection when interactions were also present. Third-order terms were not supported due to high collinearity with second-order terms (tolerances less than 0.10). Note that we initially divided our analysis of resource selection for each hind into two seasons (May–October and November–April) in anticipation of interactive effects between resource selection and seasonal food availability on LRS. Here, we included the identification number of a hind as a random effect in a mixed model (two RSF models explaining LRS per hind); however, after failing to detect interactive effects with season on LRS we used only season-pooled RSF models (one RSF model per hind) in our analysis. Analyses were performed using Statistica 6.1 (StatSoft Inc., Tulsa, OK, USA) and the package ‘glmm.admb’ (Otter Research Ltd, Sidney, BC, Canada) written for R 2.1.1 (The R Foundation for Statistical Computing, ISBN 3-900051-07-0).

Figure 1.

Distribution of LRS (1.46±1.35 (mean±s.d.)) for 267 hinds living to at least age 3, Isle of Rum, Scotland, 1970–2001.

(d) Model selection and performance

We used Akaike's information criterion adjusted for sample size and overdispersion (QAIC_c; Burnham & Anderson 2002) to identify the most likely subsets of the Poisson regression model (table 1). We computed Akaike weights (w_i) to provide an approximate probability that each candidate model was the best of the proposed set (Burnham & Anderson 2002), and calculated the log-ratio χ² statistic for assessment of overall model fit. We incorporated estimates of models having w_i>0.20 into a weighted-model average (Burnham & Anderson 2002).

Table 1.

Candidate QAIC_c models describing the relationship between LRS and resource selection for hinds on Rum. (Predictors included resource selection coefficients (β_i) and interactions between a hind's selection for Agrostis/Festuca grassland (β_{Agrostis/Festuca}) and modifying effects of local density (density), variance in local density (δ density) and distance to the coast (β_distcoast²). The variance inflation factor, $\hat{c}=1.103$, was the χ² of the most complex model considered (model 3) divided by total model degrees of freedom. Number of parameters (k) includes the number of model predictors, the Poisson regression constant and the model error term. The parameter Δ_iQAIC_c refers to the change in QAIC_c between model i and the model with lowest QAIC_c score. QAIC_c weights (w_i) sum to 1.0 over all possible models. Models 1 and 2 were included in a weighted-model average (table 2). Models 1–4 were significantly different from the null (QAIC_c=773.49) at p<0.00001 (log-ratio χ²); models 5–8 were significant at p<0.003.)

model	model predictorsa	k	QAICc	ΔiQAICc	wi
1	${\beta }_i+{\beta }_{Agrostis/Festuca}\times {\beta }_{{\text{distcoast}}^2}+{\beta }_{Agrostis/Festuca}\times \text{density}$	11	751.62	0.00	0.64
2	βi+βAgrostis/Festuca×density	10	753.86	2.23	0.21
3	${\beta }_i+{\beta }_{Agrostis/Festuca}\times {\beta }_{{\text{distcoast}}^2}+{\beta }_{Agrostis/Festuca}\times \text{density}+{\beta }_{Agrostis/Festuca}\times \delta \text{density}$	13	755.13	3.51	0.11
4	βi+βAgrostis/Festuca×density+βAgrostis/Festuca×δ density	12	756.99	5.37	0.04
5	βi	8	767.82	16.20	0.00
6	${\beta }_i+{\beta }_{Agrostis/Festuca}\times {\beta }_{{\text{distcoast}}^2}$	9	768.78	17.16	0.00
7	βi+βAgrostis/Festuca×δ density	10	770.22	18.60	0.00
8	${\beta }_i+{\beta }_{Agrostis/Festuca}\times {\beta }_{{\text{distcoast}}^2}+{\beta }_{Agrostis/Festuca}\times \delta \text{density}$	11	771.58	19.96	0.00

^aFor all interactions, first-order terms of interacting parameters are included in model subsets.

We used k-fold cross-validation to evaluate predictive success of the selected model average (Hastie et al. 2001). We randomly divided our sample into 10 groups (approx. 27 hinds each) and trained our model iteratively on nine of the ten datasets. For each iteration, validation was based on the remaining testing set. We used the Spearman-rank correlation coefficient (r_s) between predicted and observed LRS among withheld hinds to assess predictive capacity.

To help interpret interactions present in the selected model, we carried out a series of model predictions in which predictor variables and covariates were varied over a range of values centred on their population means. We plotted the mean response in LRS to manipulated input variables, holding additional predictors at their mean values. We obtained means of LRS by resampling predictions of the Poisson regression model, whereby all parameters in the model were drawn from a normal distribution based on their estimates and associated uncertainty (s.e.m.).

3. Results

Coefficients of the individual-pooled RSF suggest that most hinds selected Agrostis/Festuca grassland (β_{Agrostis/Festuca}=0.622±0.020 (mean±s.e.m.)) and Juncus marsh (β_Juncus=2.526±0.083) relative to other vegetation types. Hinds generally avoided communities of Molinia flush (β_Molinia=−2.480±0.025), Calluna heath and heather moorland (β_Calluna=−2.480±0.018) and blanket bog (β_Eriophorum=−1.932±0.238). The coefficient describing selection for distance from the coast (β_distcoast²=−7.86×10⁻⁸±1.64×10⁻⁹) suggests that most animals occupied areas relatively close to the sea.

Preliminary analysis of Pearson residuals of candidate Poisson regression models highlighted three outliers associated with extremes of resource selection and/or local density; we removed these individuals for analysis. The most parsimonious Poisson regression model related an individual's LRS to first-order effects of resource selection and local density, with interactions between selection for Agrostis/Festuca grassland and the square of distance to the coast, and local density (table 1). We also considered a second model, identical to the first but without the interaction β_{Agrostis/Festuca}×β_distcoast², and included it with the best model in a weighted-model average (table 2). The predictive capacity of the weighted-model average, measured as the r_s in predicted versus observed LRS among hinds of 10 cross-validation samples, was 0.44 (p<0.001).

Table 2.

Estimates±s.e.m. of the two best Poisson regression models (table 1) and their weighted-model average describing the relationship between LRS and first- and second-order effects of resource selection (β_i) and local density (density).

parameter	model 1	model 2	model averagea
intercept	0.516±0.375	0.711±0.360*	0.564±0.337
βCalluna	−0.019±0.060	−0.052±0.059	−0.0276±0.0547
βEriophorum	0.00006±0.00014	0.00010±0.00014	0.00007±0.00012
βAgrostis/Festuca	1.143±0.267***	1.187±0.266***	1.154±0.236***
βMolinia	−0.289±0.068***	−0.248±0.065**	−0.279±0.061***
βJuncus	0.0036±0.0071	0.0022±0.0070	0.0032±0.0063
βdistcoast2	−195 167±53 293**	−193 654±51 990**	−194 794±46 784**
density	−0.0048±0.0040	−0.0080±0.0037*	−0.0056±0.0037
βAgrostis/Festuca×βdistcoast2	−99 577±46 302*		−75 012±51 899
βAgrostis/Festuca×density	−0.0148±0.0033***	−0.0136±0.0032***	−0.0145±0.0029***

^aAveraged estimates of models 1 and 2 weighted by w_i (table 1). Presented are model-averaged (i.e. unconditional) s.e.m. (Burnham & Anderson 2002).

^*p<0.05; ^**p<0.001; ^***p<0.0001.

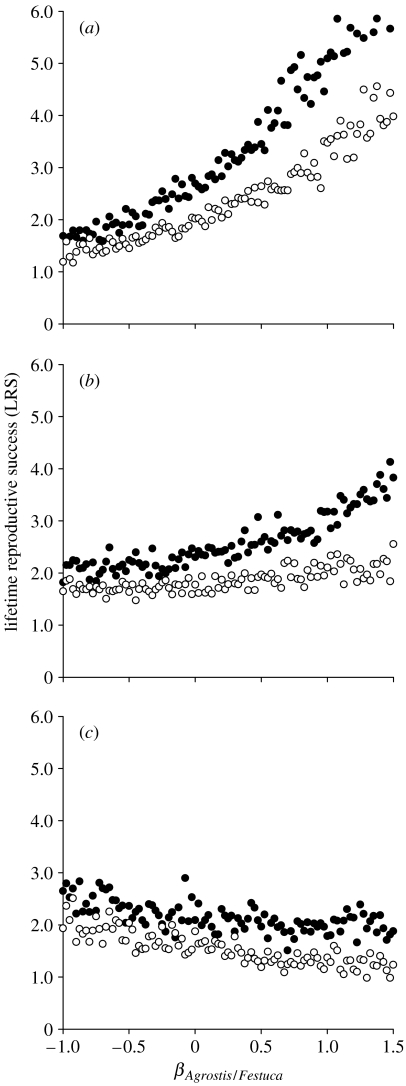
Selection for Agrostis/Festuca grassland was significantly associated with enhanced LRS (table 2). Reproductive performance also increased if hinds avoided Molinia flush (table 2), and if hinds avoided resource units with greater distances to the coast (table 2). For a given level of selection for Agrostis/Festuca grassland, LRS was predicted to be higher if selection occurred nearer the coast (interaction was significant in model 1; table 2; figure 2). LRS was inversely associated with the mean annual local density experienced by individuals during their lifetime (significant in model 2; table 2), and benefits of selecting Agrostis/Festuca grassland on reproduction significantly diminished with increasing local density (table 2; figure 2). At the highest levels of density experienced by individuals in the population, regardless of proximity to the coast, continued selection for Agrostis/Festuca grassland was predicted to negatively impact LRS (figure 2c). Although LRS was also inversely associated with variance in local density, the effect was non-significant and was a factor only in lower-ranked models (table 1).

Figure 2.

Predicted response in LRS (resampled means) with changes in β_{Agrostis/Festuca} (encompassing the mean and approximately 1 s.d. of observed values) and three levels of local density, holding all other β coefficients constant at population mean values except β_distcoast². Levels of local density include the population mean±1 s.d. (a) 47.0 hinds, (b) 72.3 hinds (mean), (c) 97.6 hinds. We varied β_distcoast² as the observed mean in β_distcoast² for hinds having centroids of movement less than 1 km from the coast (solid circles) and greater than 1 km from the coast (open circles).

4. Discussion

The strength of a hind's selection for Agrostis/Festuca grassland, compared to that of any other resource, was the greatest determinant of LRS. The importance of this resource to the reproductive success of red deer is reflected not only in the relationships presented here, but also in what can be inferred from focal observations of hind behaviour. For example, hinds increase their use of short Agrostis/Festuca grassland when accompanied by a calf (Conradt et al. 1999) and when lactating (Clutton-Brock et al. 1982). For hinds selecting Agrostis/Festuca grassland, however, interaction terms in our models suggest a trade-off between avoidance of density and selection for forage quality (figure 2). In this trade-off, the interaction β_{Agrostis/Festuca}×density appears to have a stronger influence on LRS than does β_{Agrostis/Festuca}×β_distcoast² (table 2; figure 2). This conclusion is supported by our observation that six out of eight hinds with LRS≥5 had centroids of movement within Agrostis/Festuca grasslands along Kilmory Glen, at least 1 km inland. Here, density was lower but so was forage quality. Local density of individuals with centroids of movement greater than 1 km from the coast was 48.0±1.9 hinds (mean±s.e.m.) compared to 87.4±1.2 for hinds located within 1 km of the sea (t₂₆₅=18.8, p<0.00001); the ratio of G1 : G2 grasslands within resource units containing Agrostis/Festuca differed in similar fashion (see §2b). Two hinds with centroids of movements contained within Agrostis/Festuca grassland near Shamhnan Insir (primarily G1 grassland but at intermediate density) also had exceptionally high LRS.

Our detection of spatial variation in fitness among hinds suggests a departure from Fretwell & Lucas's (1970) ideal-free distribution (IFD) model of habitat selection, although density-dependence in resource selection was clearly evident. In the IFD model, individuals are free to occupy the habitat most suitable to them, whereby suitability (fitness return) is assumed from density-dependent effects within a habitat. Here, ‘habitat’ is considered to be ‘homogeneous with respect to the physical and biological features most relevant to the behaviour and survival of the species’ (Fretwell & Lucas 1970, p. 3). In our application, we make the logical extension that individuals, rather than selecting for a homogeneous habitat type, are free to adopt the most suitable resource selection pattern (function) available to them. RSFs permit us to study the relationship between fitness and distribution in a manner that better reflects how habitat is perceived by organisms (i.e. in terms of the ecological niche).

Although our main conclusion differs from that of Conradt et al. (1999), who concluded that red deer on Rum are ideal-free distributed, the results of Conradt et al. largely support this study. Discrepancy in our main conclusions is probably based on differences in approach and scope of analysis. In particular, Conradt et al. conducted their study as a univariate correlation between LRS and percentage use of grasslands exclusive to short Agrostis/Festuca grassland (G1); however, the majority of G1 grassland was located near the coast (74.9% of all G1 grassland was less than 1 km from the sea). It is not surprising, therefore, that Conradt et al. detected a non-significant, negative correlation between LRS and grassland use: in effect, the authors modelled relationships consistent with the transition from figure 2b to 2c. Their observation of significant, negative correlations between winter survival of male calves and yearlings in response to increased selection for G1 grassland confirms our observation that when hind density is highest, avoidance of Agrostis/Festuca grassland may in fact improve LRS (figure 2c). Conradt et al. did note that differences in mean LRS for clusters of hinds in the study area might indicate departure from IFD at the larger scale. We probably captured this observed heterogeneity by including a hind's selection for both G1 and G2 grasslands in our analysis.

So why might deer not be ideal-free distributed? IFD relies on assumptions that may not always be true, and in our case, the assumption of equal availability of habitat for all hinds may have been violated if hinds were prevented from accessing all parts of the study area through social constraints we have yet to fully understand. For example, Clutton-Brock et al. (1982) observed higher frequencies of agonistic interactions between hinds, including visual threats, kicking and biting when food shortages occurred through time (e.g. in winter compared to summer), and it is possible that active defence of high-quality resources also occurred in space. More likely, however, is that departure from IFD was based on heterogeneous population growth across the study area after culling of the population ceased in 1972. Since that time the number of hinds in the study area has trebled. The greatest increase in local densities was observed in Kilmory Glen, where culling was highest due to access provided by a road along the Kilmory River. Hinds inhabiting Kilmory Glen were presumably further from carrying capacity after culling ceased compared to coastal regions, and it is possible that the density interaction we observed was due to spatial differences in proximity of the local population to carrying capacity. Our results suggest that the relationship between fitness and resource selection erodes as density increases (figure 2), as predicted by ideal-free theory (Fretwell & Lucas 1970). We did not observe interactions consistent with the ideal despotic distribution (Fretwell & Lucas 1970; Morris 2003), e.g. as density increases monopolization of resources by some individuals intensifies heterogeneity in LRS within the population. Thus, despite the current suggestion of departure from IFD, hinds on Rum may be gradually achieving this distribution.

Our approach enables us to ask ultimate questions about the spatial distribution of abundance when resource selection is viewed as a multi-variable phenomenon. We show how model interaction terms can help identify trade-offs in LRS between selection for quality within a heterogeneous resource type and avoidance of competition, in addition to testing expectations regarding the spatial distribution of fitness. Our methods may also prove useful for addressing similar trade-offs between resource use and predation risk (Werner et al. 1983; Lima & Dill 1990; Lima 1998; McLoughlin et al. 2005). Linking LRS to RSF analysis further presents some practical applications to conservation biology. For example, our methods may lead to greater insight into what constitutes ‘critical habitat’ for a species (i.e. habitat linked to survival and reproduction), which may differ from what is suggested from RSF analysis alone (Garshelis 2000). In our application, although Juncus-dominated marsh was the highest ranked resource based on relative use versus availability—and might thus be assumed to be critical habitat for red deer—selection for Juncus marsh had little effect on LRS. Spatially mapping expected LRS overlaying an RSF may be useful for identifying instances of maladaptive resource selection, for example, where habitats are modified by humans but animals have yet to alter their resource selection strategies in a way that maximizes fitness (Delibes et al. 2001). Further, equations estimating the demographic response of individuals to resource selection may prove useful in the development of habitat-based population viability models (e.g. Akçakaya 2000).