Reputation and the evolution of cooperation in sizable groups

Abstract

The evolution of cooperation in social dilemmas has been of considerable concern in various fields such as sociobiology, economics and sociology. It might be that, in the real world, reputation plays an important role in the evolution of cooperation. Recently, studies that have addressed indirect reciprocity have revealed that cooperation can evolve through reputation, even though pairs of individuals interact only a few times. To our knowledge, most indirect reciprocity models have presumed dyadic interaction; no studies have attempted analysis of the evolution of cooperation in large communities where the effect of reputation is included. We investigate the evolution of cooperation in sizable groups in which the reputation of individuals affects the decision-making process. This paper presents the following: (i) cooperation can evolve in a four-person case, (ii) the evolution of cooperation becomes difficult as group size increases, even if the effect of reputation is included, and (iii) three kinds of final social states exist. In medium-sized communities, cooperative species can coexist in a stable manner with betrayal species.

1. Introduction

The formation and maintenance of cooperation in social dilemmas has attracted considerable attention in various fields such as sociobiology, economics and sociology. They are often explained by inclusive fitness or by reciprocity. The theory of inclusive fitness, as presented by Hamilton (1964), claims that cooperative behaviour can be facilitated by genetic relatedness. However, cooperation among genetically non-related individuals is often observed in actual ecosystems and in human societies (Connor & Norris 1982; Wilkinson 1984; Fehr & Fischbacher 2003). To explain such cooperation, the (direct) reciprocity theory, which assumes that individuals who help a recipient get direct returns from the recipient, was first proposed by Trivers (1971). Later, Axelrod (1984) formalized the reciprocity theory using the two-person iterated Prisoner's Dilemma game. He showed that reciprocity based on the so-called ‘Tit-for-Tat’ strategy results in a stably cooperative society. His work is quite influential because his theory, which is based only on the strategic interactions among individuals, does not require kinship to explain the emergence of cooperation. However, it is important to note that his model assumes that interactions are dyadic and that each individual repeatedly interacts many times with every other individual (round robin tournament of the two-person iterated Prisoner's Dilemma game among individuals in the population).

On the other hand, the indirect reciprocity theory, first suggested by Alexander (1979), states that individuals who help a recipient do not necessarily receive some direct return from the recipient, but from someone else in the community. The model of indirect reciprocity formalized by Nowak & Sigmund (1998a,b) involves image scoring (evaluating the reputation of individuals in a group). That study showed that indirectly reciprocal cooperation based on a discriminating strategy, which only allows cooperation with an individual who has a good image score, evolves through the effect of reputation and results in a stably cooperative society, even though pairs of individuals interact only a few times. Subsequent to their work, various studies have specifically examined the indirect reciprocity theory (Lotem et al. 1999; Leimar & Hammerstein 2001; Fishman 2003; Mohtashemi & Mui 2003; Panchanathan & Boyd 2003; Brandt & Sigmund 2004; Johnstone & Bishary 2004; Ohtsuki 2004; Ohtsuki & Iwasa 2004). Moreover, Nakamaru & Kawata (2004) showed that rumours have a great effect on the evolution of cooperation in human societies in which individuals can transmit rumours to others and can spread false rumours.

Note that both Axelrod's reciprocity model and most indirect reciprocity models, including Nowak's model, have presupposed dyadic interactions. However, social dilemmas in real communities usually involve three or more individuals. Joshi (1987) and Boyd & Richarson (1988) investigated the n-person iterated Prisoner's Dilemma game (n>2) and found that the condition that allows the evolution of reciprocal cooperation becomes restrictive as group size increases. Consequently, reciprocity theory has been shown to be inapplicable for explaining the evolution of cooperation in large communities.

In spite of these findings, we sometimes observe that human beings and some kinds of animals cooperate with others in large real world communities (e.g. donations of blood or money for charity and alarm calling in a flock of birds). Moreover, experimental studies have shown that human beings cooperate in large communities (Marwell & Ames 1978, 1980). Therefore, the mechanism of the evolution of cooperation in large groups remains unclear.

It might be that, in the real world, reputation plays an important role in the evolution of cooperation. For example, at some Internet auction sites, each participant has a reputation and can observe the reputations of others. Presumably, this system has a deterrent effect against fraud. Various experimental studies have reported that the effect of reputation facilitates the evolution of cooperation in human societies (Wedekind & Milinski 2000; Milinski et al. 2001, 2002a,b). Moreover, observation by bystanders is an important factor of reputation. Several studies have demonstrated that observation by bystanders strongly influences some kinds of animals' behaviour (Oliveira et al. 1998; Doutrelant et al. 2001; Bshary 2002).

To our knowledge, no studies have analysed the evolution of cooperation in large communities where the effect of reputation is included. The present study investigates the evolution of cooperation in larger groups where the reputation of individuals affects the decision-making process (see table 1). Results of this study demonstrate the following: (i) cooperative behaviour can evolve in a four-person case, (ii) the evolution of cooperation becomes difficult as group size increases, even if the effect of reputation is included, and (iii) three kinds of final social states exist. In medium-sized communities, cooperative species can coexist with betrayal species.

Table 1.

The position of the present study.

	two-person game	n-person game
iterated game (direct reciprocity)	Axelrod (1984)	Joshi (1987) and Boyd & Richarson (1988)
reputation game (indirect reciprocity)	Nowak & Sigmund (1998a,b)	present study

2. Model

This study investigates the evolution of cooperation observed in social dilemmas played in sizable groups. In these games, each individual has a strategy to make a decision based on the reputations of the group members. Each of these individuals has an ‘image score’ as a reputation, which either improves or worsens according to past behaviours. To reveal evolutionary phenomena in this type of game, we conducted computer simulations with a selection/reproduction process that increases the population of good performing strategies.

Let us consider a population of n individuals. In each round, g(≥2) individuals are chosen randomly from the population to form a group. They play a game in which the payoff matrix corresponds to the ‘g-person Prisoner's Dilemma game (g≥2)’.

In this game, each of the players either contributes the amount c (cost) into the public pool (‘cooperation’) or declines to contribute (‘betrayal’). The payoffs for a cooperator, π^C, and that for a betrayer, π^D, in the group are defined as

$${\pi }^{\text{C}}=(i/g)b-c$$ 2.1

and

$${\pi }^{\text{D}}=(i/g)b,$$ 2.2

where i is the number of cooperators in the group, b is the benefit produced by a cooperative act and c is the cost of cooperative act. We assume the following two constraints to consider the social dilemma situation:

1. c>b/g (Cooperation is costly for the individual.)

2. b>c>0 (Cooperation is beneficial for group.)

In this paper, we set b=0.85g and c=1. Results of this study do not change essentially, even if we choose other values for b and c that satisfy the above two conditions.

Each player has an image score, s, that ranges from −5 to +5, which can be regarded as that individual's reputation. (The same range is used in Nowak & Sigmund (1998a).) At the beginning of each generation, which comprises m consecutive rounds of the above games, image scores are reset to zero. The image score increases by one unit if a player cooperates; it decreases by one unit if the player does not cooperate. Note that an image score of any individual is known to all group members. A strategy is given by a number k (k=−5 to 6): a player with this strategy, k, cooperates if the average image score of other members of the group is at least k. (Results of experiments on human subjects indicate that human beings cooperate more frequently with others when the average reputation of other members of the group is good (Suzuki et al. submitted).) A good image score of an individual often implies a higher probability that others will cooperate with the individual.

At the end of each generation, each individual leaves offspring depending on his/her fitness. That fitness value is defined as the total payoff received during the generation (m rounds). Higher fitness implies a higher probability that the individual can leave offspring. We use the following ‘binary tournament selection’ procedure, a genetic algorithm, to select individuals:

1. Two candidates for parents are selected randomly.

2. The candidate with the higher fitness is picked to be the parent with probability 0.9; that with the lower fitness is picked with probability 0.1.

3. A copy of the parent is added to the population for the next generation. In case the population size is n, the above selection process is repeated n times.

The basic algorithm for computer simulations is described in table 2; the basic parameter settings are listed in table 3. In the remainder of this paper, we use these parameter settings and algorithms unless we specifically mention otherwise. The ratio of the population size, n, to the number of rounds, m (m/n=4), is fixed (evolutionary phenomena of the model are not fundamentally changed as far as the ratio is fixed).

Table 2.

The basic algorithm.

(i)	create an initial population of n individuals (strategies of individuals are distributed randomly from k=−5 to 6)
(ii)	g individuals are chosen randomly from the population
(iii)	these g individuals play a game
(iv)	procedures (ii) and (iii) are repeated m times
(v)	individuals leave offspring depending on their fitness
(vi)	image scores are reset to zero
(vii)	repeat procedures (ii)–(vi)

Table 3.

Basic parameter settings.

population size	n=200
group size	g=4
number of rounds in a generation	m=4n
cost of cooperation	c=1
coefficient for benefit from cooperation	b=0.85g
image score	−5≤s≤5
coefficient for strategy	−5≤k≤6

3. Results

(a) Effect of group size on the frequency of cooperation

Figure 1 shows that cooperative behaviour can evolve in the four-person case. After the 700th generation, the frequency of cooperation reaches a high level. What if the situation were to involve more than four persons?

Figure 1.

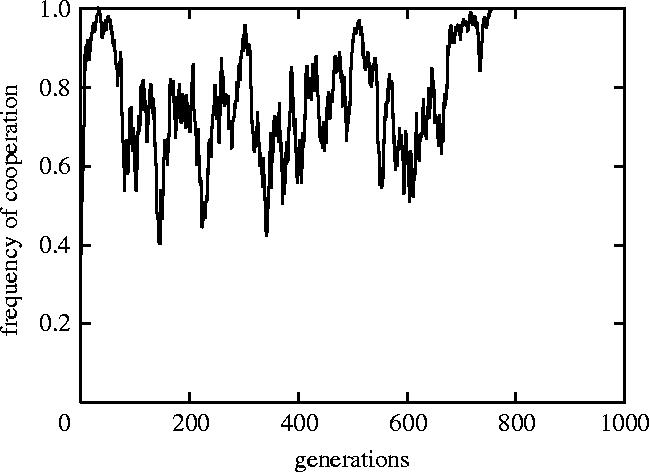
Dynamics of the frequency of cooperation in the four-person case (population size n=200; group size g=4; the number of rounds m=4n): the frequency of cooperation is plotted as a function of the generation for the first 1000 generations of the simulation. The frequency of cooperation indicates the ratio of cooperative actions to all actions within a generation.

As shown in figure 2, the frequency of cooperation decreases as the group size increases. In other words, the evolution of cooperation becomes difficult with the increase in group size, even if the reputation effect is included.

Figure 2.

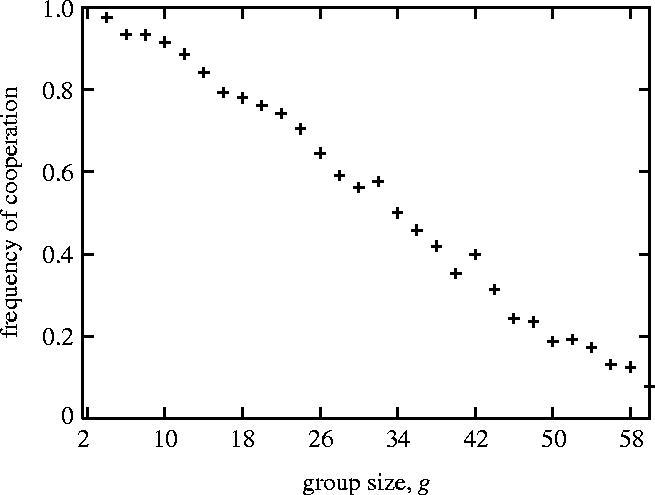
The frequency of cooperation decreases concomitantly with the increase in group size (population size n=200; the number of rounds m=4n): the frequency of cooperation at the 1000th generation is plotted as a function of group size. Each point denotes the averaged values of 1000 computer simulation runs.

(b) Effect of group size on the social phase

Results reveal that only three types of final social states exist in the evolutionary process: the first is a cooperative society, the second is a stable polymorphism of two strategies and the third is a betrayal society. In the cooperative society, all individuals always cooperate. In the betrayal society, all individuals always betray. In the stable polymorphism of two strategies, one cooperative strategy (k=−5 to 0) and one betrayal strategy (k=1 to 6) coexist in a stable manner (similar phenomena were also observed in the n-person iterated Prisoner's Dilemma models (Joshi 1987; Boyd & Richardson 1988)). Note that neither polymorphism of more than two strategies nor polymorphism of two cooperative (betrayal) strategies ever appears.

As shown in figure 3, if the group size is less than 28, the probability of the cooperative society is the highest (phase I: cooperative phase). The probability of the polymorphism is the highest if the group size is between 28 and 45 (phase II: polymorphism phase). The probability of the betrayal society is highest if the group size is greater than 45 (phase III: betrayal phase). Hence, the social phase gradually changes from the cooperative phase to the betrayal phase as the group size increases. In some group sizes between the cooperative phase and the betrayal phase, the polymorphism phase appears. Figure 4 indicates a typical evolutionary process towards polymorphism.

Figure 3.

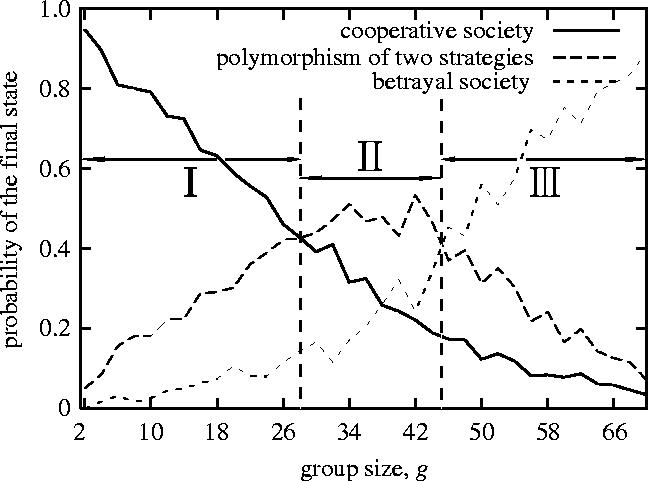
The effect of group size on the change of the social phase (population size n=200; the number of rounds m=4n): each line denotes the probability of the final social state over 1000 computer simulation runs. Phase I: cooperative phase, phase II: polymorphism phase, phase III: betrayal phase.

Figure 4.

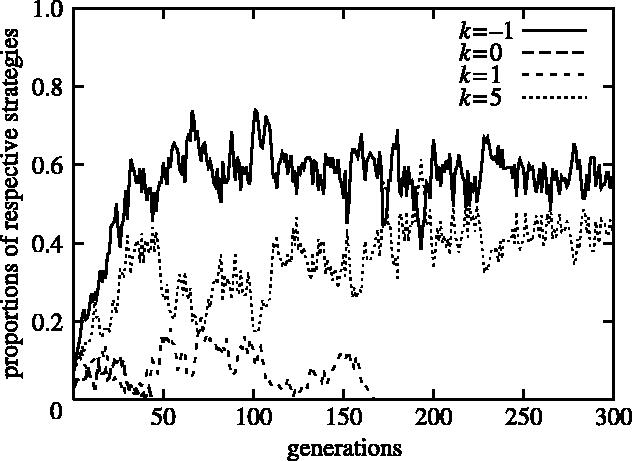
A typical evolutionary development towards the polymorphism of two strategies (population size n=200; group size g=20; the number of rounds m=4n): the proportions of respective strategies in the population are plotted as functions of the generation for the first 300 generations of the simulation.

The typical evolutionary process to polymorphism is that most strategies become extinct in early generations. After wholesale extinction, one betrayal strategy remains along with one cooperative strategy that is tolerant of others with not-extremely-bad reputations. In the example depicted in figure 4, strategies other than k=−1, 0, 1, 5 become extinct in early generations. k=0 and k=1 also become extinct by the 200th generation. The remaining strategies are k=−1 (cooperative) and k=5 (betrayal), which coexist in a stable manner. Additionally, we can presuppose various types of strategies for decision making that are based on image scores. The results of the computer simulation which involves those strategies are given in Appendix A.

4. Summary and discussion

When we meet an unfamiliar person in daily life, or when we enter a community with unfamiliar faces, we often consider the reputation of that person to decide how we ourselves should behave towards them (Wedekind & Milinski 2000; Milinski et al. 2001, 2002a,b). In consequence, we can sometimes believe them, based on their reputation, and thereby form cooperation. Nowak & Sigmund (1998a,b) show, through analyses of computer simulation results and an analytical model, that indirectly reciprocal cooperation based on a discriminating strategy (cooperates only with an individual who has good reputation) can evolve through the effect of reputation.

However, we should note that formation of cooperation may become difficult with increased community size, even if the reputation of individuals can be observed, because it is hard to identify the reputation of each individual in a large community. For that reason, we may behave cooperatively towards a selfish individual who would take advantage of our cooperation. This study examined how the success or failure of such a reputation-based cooperation is related to group size.

The results of the computer simulation have revealed the following three points. First, the frequency of cooperation achieves a very high level in the four-person case. Hence, as in the two-person case obtained by Nowak & Sigmund (1998a,b), indirectly reciprocal cooperation can evolve through the effect of reputation even in the four-person case.

Second, the formation of cooperation becomes difficult as community size increases, even if the effect of reputation is included. This fact implies that we cannot be so optimistic about the effect of reputation on the formation of cooperation in large communities. On the other hand, in the real world, we often witness cooperation in communities comprising more than two individuals. Therefore, we cannot perfectly explain the formation and maintenance of cooperation in large communities solely by the effect of reputation.

Third, between small and large group sizes that mostly engender cooperative and betrayal societies, respectively, there exists a range of medium group sizes that tend towards polymorphism of cooperative and betrayal strategies. This tendency is similar to that encountered in the ecology of the n-person iterated Prisoner's Dilemma game, wherein a tolerant reciprocal strategy, that continues to cooperate despite a certain number of betrayals in a group, coexists in a stable manner with a betrayal strategy. This result implies that, in the real world, cooperative species can coexist with betrayal species in medium-sized communities.

Appendix A

So far, we have assumed that individuals determine their own behaviour based only on the average image score (reputation) of other members in the group. However, we can presuppose various strategies for decision making that are based on image scores (Nowak & Sigmund 1998a; Brandt & Sigmund 2004; Ohtsuki & Iwasa 2004).

We explored three types of strategies. The first is a DIS strategy, which is given by a number k (k=−5 to 6). The second is an OR strategy, which is represented by k (k=−5 to 6) and h (h=−5 to 6). The third is a MIN strategy, which is expressed by a number k (k=−5 to 6). An individual who adopts the DIS strategy cooperates if the average image score of other members in the group is at least k. In other words, the DIS strategy is identical with the strategy that is used in the main model (see §2) of the paper. An individual using the OR strategy cooperates if the average image score of other members in the group is at least k or if her own image score is less than h. An individual with a MIN strategy cooperates if the minimum image score of other members in the group is at least k.

On the other hand, we also have presumed complete information, whereby each individual can always know others' exact image scores. This assumption is unrealistic. It is more realistic to assume incomplete information, by which each individual is sometimes unable to assess the image scores of others accurately. In the incomplete information situation, each individual fails to assess other individuals' image scores with probability q, and then randomly estimates the reputation of the individual within the range −5 to +5.

We performed the computer simulation (described in §2) under the following three situations. The first is that individuals adopt an OR strategy and the information about the image score of the others is complete (OR-complete). The second is that individuals adopt a MIN strategy and the information about image scores of the others is complete (MIN-complete). The last situation is one in which individuals adopt a DIS strategy and the information about the image scores of others is incomplete (DIS-incomplete). Note that the situation that is the same as the basic model in §2 corresponds to DIS-complete.

As shown in figure 5, in all three situations the frequency of cooperation decreases as the group size increases. This fact implies that, as in the basic model in §2, the formation of cooperation becomes difficult as the community size increases in all three situations described above.

Figure 5.

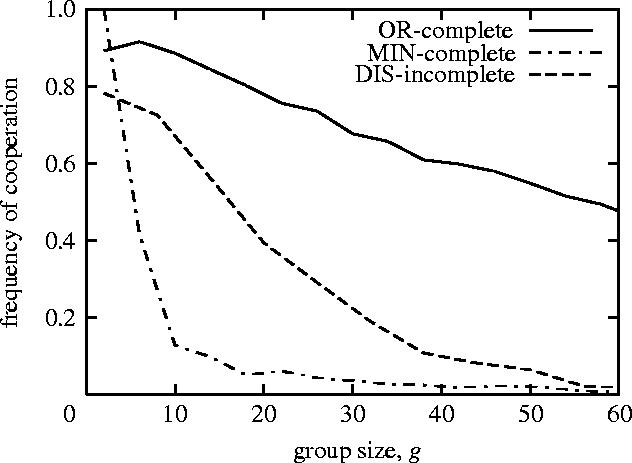
The frequency of cooperation decreases with the increase in group size (population size n=200; the number of rounds m=4n): the frequency of cooperation at the 1000th generation is plotted as a function of group size. Each point denotes the averaged value over 1000 computer simulation runs in the three situations (OR-complete, solid line; MIN-complete, dash-dotted line; DIS-incomplete (q=0.5): short-dashed line).