Knowledge Discovery from Structured Mammography Reports Using Inductive Logic Programming

Abstract

The development of large mammography databases provides an opportunity for knowledge discovery and data mining techniques to recognize patterns not previously appreciated. Using a database from a breast imaging practice containing patient risk factors, imaging findings, and biopsy results, we tested whether inductive logic programming (ILP) could discover interesting hypotheses that could subsequently be tested and validated. The ILP algorithm discovered two hypotheses from the data that were 1) judged as interesting by a subspecialty-trained mammographer and 2) validated by analysis of the data itself.

INTRODUCTION

Knowledge discovery and data mining techniques aim to extract useful knowledge from large databases. The rapid growth of biomedical data has created an opportunity to use these methodologies to discover important hypothesis in a given domain that would be difficult to otherwise unearth. Large data repositories are being constructed in the radiology community that can be used to discover new relationships between imaging findings and diagnoses using these machine learning techniques. For example, millions of mammograms are reported each year, many of which are collected as large repositories of imaging findings and gold standard outcomes well-suited to this type of knowledge discovery. In this project, we use a large collection of mammography reports to test the feasibility of using specific knowledge discovery techniques to discover interesting correlations between patient risk factors, imaging findings, and diseases of the breast that may warrant further investigation.

Inductive logic programming (ILP) provides algorithms to learn hypotheses, expressed as logical rules. ILP assumes (a) background knowledge B, e.g., the database; (b) a language specification L telling how to construct hypotheses; (c) an optional set of constraints I on acceptable hypotheses; and (d) a finite set of examples E.¹ E is the union of a nonempty set of ``positive'' examples E+, and a set of ``negative'' examples, E-. The aim of an ILP system is to find a set of rules (H), in the form of a logic program, that cover all of the positive examples and none of the negative examples. ILP has distinct advantages to other data mining techniques because it can facilitate the interaction between humans and computers by using background knowledge to narrow the search space and return human-comprehensible results, thereby taking advantage of both the computer's speed and the human's knowledge and skills.

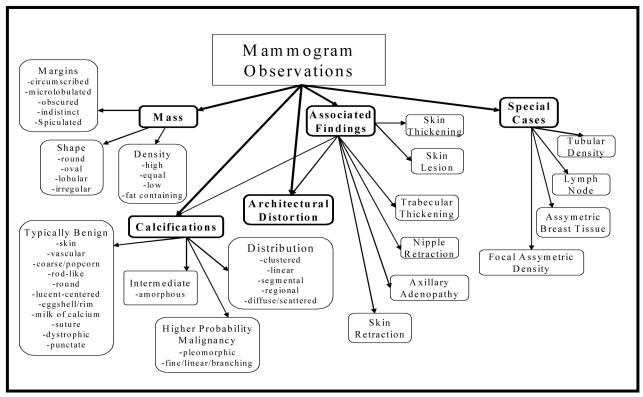
Breast cancer screening with mammography is an excellent area in medicine to apply ILP techniques for knowledge discovery. First, a standardized lexicon called the Breast Imaging Reporting and Data System (BI-RADS) has been established for the reporting of mammographic abnormalities.² BI-RADS provides descriptors for findings on mammograms as well as categories to summarize the recommendations of the interpreting physician. The BI-RADS lexicon consists of 43 descriptors organized in a hierarchy. (Figure 1) There are six BI-RADS categories (Table 1) that summarize the radiologist’s opinion of the entire study. Second, because mammography practice is heavily regulated; structured reporting is used to support required audits. Structured data, in contrast to the free text found in other areas of radiology, facilitates the use of ILP techniques. Third, the breast imaging community has developed a database format, the National Mammography Database (NMD), which standardizes data collection. Participation in the NMD initiative has motivated all mammography structured reporting vendors to develop export methods for this format. The availability of a structured lexicon, structured reporting, and a uniform database output format provides an opportunity for applying ILP techniques in the domain of mammography that would be difficult in other clinical areas.

Figure 1.

BI-RADS lexicon (general categories are in bold)

Table 1.

BI-RADS Categories

Category	Meaning
BI-RADS 0	Needs additional imaging
BI-RADS 1	Negative
BI-RADS 2	Benign
BI-RADS 3	Probably Benign
BI-RADS 4	Suspicious
BI-RADS 5	Highly suggestive of malignancy

MATERIALS AND METHODS

We collected data for all screening and diagnostic mammography examinations that were performed at the Froedtert and Medical College of Wisconsin Breast Imaging Center between April 5, 1999 and February 9, 2004. The database consisted of 47,669 mammography examinations on 18,270 patients. All of the mammographic findings, a total of 65,892, were described and recorded individually using BI-RADS. Each record in the database represented an abnormality on a patient’s mammogram recorded in the database when the radiologist generated the final report. The mammography examinations were reported in the Penrad® system (Plymouth, Minnesota) which recorded patient demographic risk factors, mammography findings, pathology results and biopsy results in structured format. This data was consolidated in the NMD format and de-identified prior to our experiment. The institutional review board determined that this retrospective study was exempt from requiring informed consent.

Masses and microcalcifications are the most common concerning findings on mammography. Table 2 provides an overview of the most important fields in the database that were used by the ILP algorithms to generate rules. Because there was often more than one finding per mammographic study, the patient information was repeated for each abnormality recorded for a given patient. Since very few findings were explicitly labeled as negative, we inferred negative findings based on missing values.

Table 2.

Important fields in NMD

Patient information	Abnormality location	Mass descriptors	Calcification descriptors
Age	Side	Shape	Shape
Hormone therapy	Depth	Density	Distribution
Family medical history	Clock location	Margins	Stability
Personal medical history	Quadrant location	Stability

We use Srinivasan’s “A Learning Engine for Proposing Hypotheses” (Aleph) ILP System.³ Aleph was set to use Muggleton’s Progol algorithm that learns rules from examples.⁴ In order to use Aleph, the NMD data were converted into Prolog facts. The conversion was straightforward and automatic: each row in the database was translated into a number of Prolog facts, one per column. We further added two predicates. One connects two findings on the same mammogram, and the other connects a finding with previous findings in the patient’s history.

Aleph tries to find one set of rules, that we call the hypothesis H. H must be constructed using the language L, such that: 1) H respects the constraints I; 2) the positive examples, E+, are explainable from the background knowledge B and the hypothesis H, and 3) the negative examples, E-, cannot be explained from B and H. In our context, B corresponds to the features taken from the mammography database. Positive examples are represented by cases labeled as malignant while negative examples are represented by cases labeled as benign. By default, Aleph constructs the hypothesis by starting from an empty set and then greedily searching for the best rule that explains an unexplained positive example. The example we try to cover next is called the seed example. To find a rule explaining the seed, Aleph first saturates this example, and then performs an admissible search over the space of rules that subsume this saturation, subject to a user-specified clause length bound. The saturation step works as follows: starting from the seed example, Aleph searches the database for the facts known to be true about that specific example. Muggleton’s insight is that a combination of thesis facts should explain this example, and that it should be possible to generalize that combination so that it will also explain other examples.⁴ The search step thus executes by generating combinations of the generalized facts. Search usually starts from the combinations that lead to smallest rules, and is constricted by providing maximum bound on rule length and on the number of rules that can be tested. Throughout, we search for rules with best performance. Performance of a rule depends on how well the rule covers (explains) positive examples and does not cover negative examples. We quantify performance using the m-estimate, a smoothed ratio between the number of positive examples covered and the total number of examples covered.

Once the ILP algorithms generated rules, a subspecialty-trained breast imaging radiologist reviewed the ILP rules and judged whether they revealed interesting patterns.

RESULTS

Aleph generated several million rules, from which the radiologist evaluated the best 130 rules. The radiologist identified 2 potentially interesting hypotheses. Those rules were:

RULE 1: is_malignant(A) :-

'BIRADS_category'(A,b5), 'MassPAO'(A,present),

'Age'(A,age6570),

previous_finding(A,B,C), 'MassesShape'(B,none),

'Calc_Punctate'(B,notPresent),

previous_finding(A,C), 'BIRADS_category'(C,b3).

This rule states that if finding (A) was:

• classified as BI-RADS 5,

• had a mass present

in a patient who:

• was between the ages of 65 and 70

• had two prior mammograms (B, C)

and prior mammogram (B):

• had no mass shape described

• had no punctate calcifications

and prior mammogram (C):

• was classified as BI-RADS 3

then it is malignant. This rule identified 7 malignant mammographic findings without misclassifying any benign findings as cancer. This rule is interesting because it finds a relationship between a malignant finding in a patient that had a previous abnormality judged to be probably benign. This may represent a delay in diagnosis if the abnormality interpreted as probably benign corresponds to the finding later diagnosed as cancer

In order to investigate the true value of this rule, queries of the database were performed. All cases that were labeled as BI-RADS 3 and subsequently diagnosed with cancer were analyzed to determine if the two abnormalities were in fact the same (Table 3).

Table 3.

Abnormalities corresponding to Rule 1

BI-RADS 3 abnormality					BI-RADS 5 abnormality
abnormality	side	clock	depth	quad	abnormality	side	clock	depth	quad	match
Clustered calcifications	L	12	M	UO	High density spiculated mass	L	C	M	*	possible
Ill-defined oval mass	R	11	M	UO	High density spiculated mass	R	11	M	UO	yes
Oval circumscribed mass	R	12	A	UI	Oval spiculated mass	R	5	P	UI	no
*	R	4	M	*	Round spiculated mass	R	4	M	LI	yes
Oval mass	R	12	P	UO	Irregular spiculated mass	R	12	P	UO	yes
Ill-defined oval mass	R	2	P	LI	Irregular high density mass	R	2	P	LI	yes
*	L	12	M	UO	Irregular spiculated mass	L	1	M	UO	possible

Note— * signifies missing data

Side: L = left, R = right

Clock: C = central

Depth: A = anterior, M = middle, P = posterior

Quad (quadrant): UO = upper outer, UI = upper inner, LO = lower outer, LI = lower inner

We concluded that abnormalities were the same if the location descriptors matched. The position of abnormalities in the breast are designated by side (right or left), clock-position (1-12 or central), depth (anterior, middle, posterior), and quadrant (upper outer, lower inner, etc.) Four of the seven cases exhibit virtually identical location descriptors for the BI-RADS 3 and the BI-RADS 5 abnormalities and are therefore likely the same findings. Two cases are possible matches with slightly different location descriptors and one case did not match

RULE 2: is_malignant(A) :-

'BIRADS_category'(A,b5),

'MassPAO'(A,present),

'MassesDensity'(A,high),

'HO_BreastCA'(A,hxDCorLC),

in_same_mammogram(A,B),

'Calc_Pleomorphic'(B,notPresent),

'Calc_Punctate'(B,notPresent).

This rule states that if finding (A) was:

• classified as BI-RADS 5,

• had a mass present

• had a mass with high density

in a patient who:

• had a prior history of breast cancer

• had an extra finding on same mammogram (B)

and extra finding (B):

• had no pleomorphic microcalcifications

• had no punctate calcifications

then it is malignant. This rule identified 42 malignant mammographic findings while misclassifying 11 benign findings as cancer. This rule is interesting because it finds a relationship between malignant and high density masses. In general mass density has not been previously thought to be a highly predictive feature.

In order to analyze the second rule, the proportion of masses diagnosed as cancer that were high density was compared with the proportion of benign masses that were high density. We found statistically significant differences in the rate of malignancy when comparing based on mass density. We combined the fat density and low density descriptors for this analysis (there was no statistically significant difference of malignancy in these two groups). Fisher's exact test demonstrated significant differences in the rate of malignancy for high density versus fat- or low-density masses, high density versus equal density masses, and equal density versus fat- or low-density masses (p < .001 for all three comparisons).

DISCUSSION

In our experiment, we have discovered two interesting hypotheses using ILP techniques and a large structured mammography database. The first hypothesis revealed at least 4 cases in which an abnormality was characterized as probably benign later discovered to be breast cancer. To appreciate the significance of this rule, one must understand the characterization of a probably benign finding on mammography. Category 3: probably benign was developed based on a prospective study that showed that several mammographic scenarios have a small probability of malignancy.⁵ A circumscribed mass, round calcifications, or a focal asymmetric density under certain circumstances is likely to be benign and biopsy can safely be deferred. The standard management of a probably benign finding is short-term follow-up (in 6 months) to reevaluate the finding. The available evidence supports the fact that the small number of cancers in this group would have an excellent prognosis when they were discovered at follow-up.

Since the institution of the BI-RADS 3 category, it has engendered significant controversy primarily because radiologists demonstrate extreme variability in its application but little is known about the impact of this variability on the efficacy of screening. Abnormalities that do not fit the strict criteria set out by the evidence, if followed, may constitute an unnecessary delay in diagnosis. Therefore, the recognition of such cases provides valuable quality assurance. The discovery of a pattern of probably benign findings later diagnosed as malignant could help to improve mammography performance in the future. Review of the films would be the next important step in order to teach radiologists how to avoid these delays in the future, mold appropriate use of the BI-RADS 3 category, and discover whether the possible matches discovered by our ILP experiment add 2 additional cases to this group.

The second rule discovered by our experiment demonstrates that the density of a mass is highly predictive of malignancy. This fact has not been documented before in the literature. In fact, in our cases, 493 biopsies might have been avoided if fat-containing masses had been considered benign. The hypothesis discovered by our ILP algorithms warrants further investigation in order to determine whether it can be used to improve the predictive value of mammography to avoid unnecessary breast biopsy.

In general, our experiment shows that data mining using ILP techniques can discover novel and interesting hypotheses. In fact, we accomplished this with a relatively small sample of mammograms from a single practice. Approximately 40 million mammograms will be performed in the United States in the next 1 to 2 years based on census data and breast cancer screening rates.^{6, 7} The massive amount of data generated by screening mammography provides a unique opportunity for the machine learning and breast imaging communities to work together to improve mammography. In the domain of breast cancer screening, ILP methods hold great promise to enable physicians to learn from data to improve early detection and characterization of breast cancer in imaging.

Table 4.

Density of benign vs. malignant masses

Mass Density	Benign (%)	Malignant (%)	Total
Fat-density	493 (100)	0 (0)	493
Low	3406 (99.9)	2 (.1)	3408
Equal	496 (96.7)	17 (3.3)	513
High	221 (68.2)	103 (31.7)	324
Total	4616 (97.4)	122 (2.6)	4738