Conformational Study of Met-Enkephalin Based on the ECEPP Force Fields

Abstract

We report a computational study of the small peptide Met-enkephalin based on the ECEPP/2 and ECEPP/3 force fields using the basin paving method. We have located a new global minimum when using the ECEPP/3 force field with peptide angles ω fixed at 180°. With this new result, we can conclude that the lowest energy configurations of Met-enkephalin predicted based on all four versions of ECEPP have a classic γ-turn centered at residue Gly³ and a β-turn at residues Gly³-Phe⁴. However, minor differences between the structures also exist.

INTRODUCTION

In computer simulations of protein folding, small peptides are often used as model systems for uncovering the physical properties of larger systems. From a computational perspective, small peptides are also ideal benchmarks for evaluating the efficiency of newly developed computational algorithms for protein folding. It is possible to thoroughly search the configuration space of a short peptide within a reasonable amount of computational time—such thoroughness is required to reveal the general physical properties of protein folding.

Met-enkephalin, first identified from the enkephalin mixture from brains (1), is one of the most used model peptides. It has a short residue sequence of Tyr¹-Gly²-Gly³-Phe⁴-Met⁵. Met-enkephalin is an endogenous opioid pentapeptide found in brains, pituitary and peripheral tissues, and is involved in a variety of physiological processes. Experimental studies showed that this peptide exhibits several different structures in aqueous solutions (2).

In computer simulations of this peptide, especially in those adopting the ECEPP/2 (3,4) or ECEPP/3 (5) force fields, NH₂ and COOH are often chosen as the N-terminus and C-terminus neutral groups, respectively. The pentapeptide consists of a total of 75 atoms described by 24 independent backbone and side-chain dihedral angles. Even such a small peptide gives rise to a complex conformational space, and the total number of local minima was estimated to be no less than 10¹¹ (6). Because of the complexity in its configuration space and the short sequence allowing significant computational studies, Met-enkephalin has been extensively studied computationally (6–34), and has been regarded as a benchmark model used frequently for testing simulation methods (14,16–19,29–33) in recent years.

The lowest energies of Met-enkephalin without explicit solvation effects were previously determined based on the ECEPP/2 potential (6,10–12,14,15) and the ECEPP/3 potential (11,13). Local energy minima not much higher than global minima were sampled and classified by Freyberg and Braun (10) based on the ECEPP/2 potential, and by Eisenmenger and Hansmann (11) based on both ECEPP/2 and ECEPP/3 potentials (with the peptide dihedral angles ω fixed at 180°). Using the mutually orthogonal Latin-squares technique, Vengadesan and Gautham (21) performed the conformational studies of this peptide based on the ECEPP/3 potential, and compared the structures with those of Leu-enkephalin. Hansmann and co-workers studied the energy landscape (8), characteristic temperatures (35), and thermodynamics and kinetics (7) of folding of the peptide using the ECEPP/2 potential. Employing the reference interaction site model and various simulation methods, Kinoshita et al. (25,26) and Mitsutake et al. (27,28) studied Met-enkephalin in aqueous solutions. Berg and Hsu (29), using this peptide as a model protein, discussed various solvent-accessible area methods. Shen and Freed (30) performed a comparison study of explicit and implicit solvent effects by adopting this peptide as the model. Carlacci (20) analyzed the conformations of the peptide with the consideration of solvation and ionization. Using Met-enkephalin as a testbed, Zaman et al. (31) compared the peptide's dynamical properties implied by different force fields and suggested that a significant difference can be generated between the explicit-atom and united-atom potentials. Montcalm et al. (32) compared the differences between the global minimum structures of the peptide, obtained based on ECEPP/2, AMBER, and CHARMM force fields. Using the parallel tempering simulation method (36,37), Evans and Wales (9) analyzed the lowest energy conformations, the free energy landscape, and the dynamics of this peptide using the CHARMM potential. Simulations were also performed by Rathore et al. (19), by extending the Wang-Landau algorithm (38,39) to continuous systems, to determine the density of states. Berg (33) used this model protein to test the newly proposed funnel transformation method, which is suitable for global optimization. From another point of view, i.e., the helical contents of its structures, Sanbonmatsu and García (34) performed a structural study of Met-enkephalin in explicit aqueous solution.

The lowest energies previously found for Met-enkephalin, without the inclusion of solvation effects, are summarized in Table 1 for four versions of the ECEPP force field: ECEPP/2 and ECEPP/3, each with the peptide angles ω fixed or relaxed. Also included in the table are some new lowest energies obtained in this work. Their conformations and comparisons with previous studies will be discussed in Results and Discussions.

TABLE 1.

The lowest energies (in kcal/mol) obtained in previous studies of Met-enkephalin and in this work based on the ECEPP/2 and ECEPP/3 force fields

Energy	Source, Reference	Force field
−12.91	(6,10,12,14)	ECEPP/2
−10.72	(11)	ECEPP/2 with ω ≡ 180°
−11.71	(13)	ECEPP/3
−10.85	(11)	ECEPP/3 with ω ≡ 180°
−12.43	This work	ECEPP/3
−10.90	This work	ECEPP/3 with ω ≡ 180°

COMPUTATIONAL METHOD

In our study of Met-enkephalin, a recently proposed stochastic optimization algorithm, the basin paving (BP) method (16,40), was employed to search for the lowest energy configurations for all four cases of the force fields. This Monte Carlo (MC) method adopts the histogram accumulation strategy (38,39,41–45) of the energy-landscape paving (41) method as one of the components, and includes a critical revision to the acceptance criterion of lower energy movements. This revision ensures that during the computational search, a new low energy configuration is always examined seriously; in the meantime, the histogram-based method promotes the probability of surpassing higher energy barriers to escape local entrapments.

As another component in BP, to precisely locate the minima of a complex energy landscape in our MC simulation, the energy itself is replaced by the reduced energy landscape (14,46–49) as the target function. Within this strategy, the original energy function, E(r), where r is a 3N-dimensional variable with N the number of representative atoms in the system, is first transformed into a reduced form, 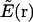, by adopting the value of a “nearby” local energy minimum, 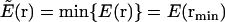, where min {…} stands for a deterministic minimization procedure that pins down the “nearby” minimum with a high precision. In our simulations we used the quasi-Newton optimization approach (50).

Computationally, at MC step t in BP, the MC transition probability between the existing configuration with a reduced energy 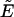and an attempted configuration with 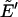can be expressed as

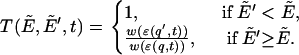(1)

In this transition probability, a Boltzmann weight

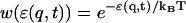(2)

is used, where k_BT is the thermal energy that needs to be externally specified in a typical MC procedure. A deformed energy,

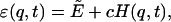(3)

is considered in the above weight, where q is a physical quantity for which the histogram H(q, t) is collected, and c is an adjustable free parameter used to optimize the search algorithm.

The method used in this article, basin paving, is an extension of the Monte Carlo with minimization (MCM) method (14), or the equivalent basin hopping (BH) method (46,47). The Boltzmann weight is used in MCM or BH, which would cause entrapment of the simulation procedure at a local minimum within limited computational time. Instead, in BP, we have introduced a generalized weighting scheme that overcomes this problem, in the same spirit as the multicanonical basin hopping method that we recently introduced (48,49). Mathematically, setting c = 0 in BP gives the same Boltzmann weight as used in MCM or BH. In comparison with multicanonical basin hopping, BP further ensures the acceptance of low energy conformations by the unconditional allowance of each low energy movement.

In these simulations, we took parameters , c = 1 kcal/mol, and T = 50 K in Eqs. 2 and 3. To compute the potential energy E based on different versions of ECEPP, we used the program package SMMP (51). For the discussion of structures presented in the next section, we have used the definition of β- and γ-turn types as listed in Table 2. Further details of the definition can be found in Richardson (52), Rose et al. (53), Hutchinson and Thomton (54), Venkatachalam (55), Némethy and Printz (56), Némethy and Scheraga (57), and Milner-White et al. (58). To determine the peptide turns for conformational analysis, the program package PROMOTIF (54) has been employed. As implemented in PROMOTIF by default (54), when determining a β-turn, these φ- and ψ-angles are allowed to vary by 30°, with a more flexible tolerance of allowing one angle to deviate by 40°. However, for a γ-turn determination, the torsional angles are all allowed to vary by 40°.

TABLE 2.

The classification of peptide turns

Turns	φi+1	ψi+1	φi+2	ψi+2
β-turns
Type I	−60	−30	−90	0
Type I′	60	30	90	0
Type II	−60	120	80	0
Type II′	60	−120	−80	0
Type III	−60	−30	−60	−30
Type III′	60	30	60	30
Type VIa	−60	120	−90	0
Type VIb	−120	120	−60	0
Type IV	Turns excluded from all the above
γ-turns
Classic	75	−64
Inverse	−79	69

An ideal β-turn is formed by four residues labeled from i to (i + 3) with the two central residues having the dihedral angles listed in the table. An ideal γ-turn is formed by three residues labeled from i to (i + 2) with the dihedral angles of the (i + 1)^st residue shown in the table. Details can be found in Richardson (52), Rose et al. (53), Hutchinson and Thomton (54), Venkatachalam (55), Némethy and Printz (56), Némethy and Scheraga (57), and Milner-White et al. (58).

RESULTS AND DISCUSSIONS

For all four versions of the force field, i.e., ECEPP/2 and ECEPP/3 with the peptide dihedral angles ω either fixed or relaxed, we list the lowest energies and their corresponding configurations obtained from BP search, in Table 3. In the table, the labels E/2 and E/3 denote the configurations obtained using ECEPP/2 and ECEPP/3, respectively. If the peptide dihedral angles ω are fixed at 180°, a subscript π is added to the labels. The graphical representation of the structures obtained is displayed in Fig. 1 from plots a–d, corresponding to the cases E/2_π, E/2, E/3_π, and E/3, respectively. Furthermore, we have explicitly drawn the hydrogen bonds by dashed lines, using the cutoff length 2.2 Å as the upper bound to identify the existence of a hydrogen bond.

TABLE 3.

Internal coordinates corresponding to lowest-energy minimum for Met-enkephalin, found in this work (columns 3–6) and previous work (last two columns)

	Torsion	E/2π	E/2	E/3π	E/3		E/3(b)
Tyr1	χ1	−179.8	−172.6	59.9	−173.2	−174.2	−173.2
	χ2	68.6	−101.3	94.1	−100.7	−85.2	−100.5
	χ6	−34.7	14.1	−21.3	13.7	2.8	13.6
	φ	−86.3	−85.8	168.1	−83.1	−162.7	−83.5
	ψ	153.7	156.2	0.9	155.8	−41.7	155.8
	ω	180.0	−176.9	180.0	−177.1	180.0	177.2
Gly2	φ	−161.5	−154.5	126.8	−154.2	65.8	−154.3
	ψ	71.1	83.7	−21.2	85.8	−87.0	86.0
	ω	180.0	168.6	180.0	168.5	180.0	168.5
Gly3	φ	64.1	83.7	83.7	83.0	−157.3	83.0
	ψ	−93.5	−73.9	−61.6	−75.0	34.9	−75.1
	ω	180.0	−170.1	180.0	−170.0	180.0	−169.9
Phe4	χ1	179.8	58.8	58.6	58.9	52.4	58.8
	χ2	−100.0	−85.4	92.9	−85.5	−96.0	−85.5
	φ	−81.7	−137.0	−128.2	−136.8	−158.8	−136.9
	ψ	−29.2	19.3	18.8	19.1	159.5	19.1
	ω	180.0	−174.1	180.0	−174.1	180.0	−174.1
Met5	χ1	−65.1	52.8	55.7	52.9	−66.1	52.9
	χ2	−179.2	175.3	−178.6	175.3	−179.6	175.3
	χ3	−179.3	−179.8	177.0	−179.9	−179.9	−179.9
	χ4	−179.9	61.4	−179.3	−178.6	60.1	61.4
	φ	−80.7	−163.6	−162.1	−163.4	−82.4	−163.5
	ψ	143.5	160.4	7.5	160.8	134.1	161.0
	ω	180.0	−179.7	180.0	−179.8	180.0	−179.8
E (kcal/mol)		−10.72	−12.91	−10.90	−12.43	−10.85	−11.71

In the columns labeled E/2 and E/3, the coordinates were obtained based on the ECEPP/2 and ECEPP/3 potentials, respectively. A subscript π indicates the fact that the peptide angles ω of the structure were fixed at 180° in the minimization process. The last two columns, labeled 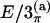and E/3^(b), contain the internal coordinates that can be found in Eisenmenger and Hansmann (11) and Androulakis et al. (13), respectively, for comparison.

FIGURE 1.

The lowest energy structures of Met-enkephalin for different versions of ECEPP force fields: (a) ECEPP/2 with ω ≡ π; (b) ECEPP/2 with ω relaxed; (c) ECEPP/3 with ω ≡ π; (d) ECEPP/3 with ω relaxed; and (e) ECEPP/3 with ω ≡ π (found in (11)). The hydrogen bonds (dashed lines) are displayed in units of Å. The figures were generated using PyMol (59).

As can be seen in Tables 1 and 3, the lowest energies that we obtained for cases E/2 and E/2_π matches previous results (6,10–12,14) exactly. The reproduced internal coordinates are listed in Table 3. According to the β-turn nomenclature defined in Table 2, the listed internal coordinates contains a Type-II′ β-turn for case E/2_π, and a Type-IV β-turn for case E/2, both at Gly³-Phe⁴. For convenience, we denote them as Gly³-Phe⁴ Type-II′ and Gly³-Phe⁴ Type-IV β-turns, respectively. Both structures also contain a classic γ-turn centered at Gly² according to the classification shown in Table 2.

The global energy minimum structures we have determined for the two cases E/2 and E/2_π contain various hydrogen bonds. In both cases, a relatively strong hydrogen bond formed by NH of Gly² and CO of Met⁵ is common. However, a hydrogen bond between CO of Gly² and NH of Gly³ appears in the global energy minimum configuration of E/2, but not of E/2_π. On the contrary, a hydrogen bond between CO of Gly² and NH of Phe⁴ can be seen in case of E/2_π, but not in E/2.

For E/2_π, the folding landscape of the peptide, together with a determination of the energy minimum, was examined in Hansmann et al. (8); the lowest-energy structure has a similar configuration to that displayed in Fig. 1 a. That configuration contains two hydrogen bonds with bond length <2.2 Å. One is formed by the amino group (NH) of residue Gly² and the carboxyl group (CO) of Met⁵, and the other is formed by CO of Gly² and NH of Met⁵. Note that the structural determination described in Hansmann et al. (8) is based on KONF90, which contains a different convention for the ECEPP force field. As a direct result, the energy minimum found in this reference cannot be directly compared with those listed in Table 1. Furthermore, according to the classification shown in Table 2, the internal coordinates in Table 3 for E/2_π contain a Gly³-Phe⁴ Type-IV β-turn. This can be contrasted with the conclusion in Hansmann et al. (8) where a Type-II β-turn was identified.

The internal coordinates of the lowest energy ECEPP/2 structure listed in Montcalm et al. (32) (which were obtained from (15) and further used for comparison with those determined from the AMBER and CHARMM force fields) are very close to those listed in Table 3. The internal coordinates in that reference suggested a Gly³-Phe⁴ Type-II′ β-turn, rather than a Gly³-Phe⁴ Type-IV β-turn obtained here based on Table 2.

When the ECEPP/3 potential with ω = 180° and with ω relaxed was used, we obtained energy minima with internal coordinates listed in the columns under E/3_π and E/3 of Table 1, respectively. The conformations of the energy minima for the two cases are plotted in Fig. 1, c and d, respectively. Both structures contain a Gly³-Phe⁴ Type-IV β-turn and a Gly³-centered classic γ-turn. The later is also a common feature in the energy-minimum structures of E/2_π and E/2.

From the torsional angles listed in Table 3, and the structures shown in Fig. 1, b and d, we conclude that the configurations of both force fields, the ECEPP/2 and ECEPP/3 potentials with ω relaxed, are very close to one another. Even the hydrogen bonds formed by these two structures are the same. However, a minor structural difference can be noticed between the energy minimum of E/3_π (Fig. 1 c) and of the other three cases. The orientation of residues Tyr¹, Gly², and the C-terminus carboxyl group COOH are pointing to different directions. As a result, the hydrogen-bond formations are different. A hydrogen bond between the CO group of Gly² and the NH group of Phe⁴ can be seen in structures Fig. 1, b and d; however, a different hydrogen bond between the CO group of Tyr¹ and the added terminus OH group, appears in the structure in Fig. 1 c.

The energy minimum for E/3_π, E = −10.90 kcal/mol, is ∼0.05 kcal/mol lower than the value previously reported in Eisenmenger and Hansmann (11). While the energy difference is not large, our new result exhibits distinctive differences in the minimum energy conformation. For convenience, we have also reproduced the internal coordinates of the later case, denoted as , in Table 3, and the corresponding structure in Fig. 1 e. Visually, we can already see the difference between plots in Fig. 1, c and e. A more careful analysis of the internal coordinates reveals that structure Fig. 1 e contains a Gly²-Gly³ Type-IV β-turn and a Gly²-centered classic γ-turn, which can be contrasted with the Gly³-Phe⁴ Type-IV β-turn and the Gly³-centered classic γ-turn of the new structure found in this work. It is also interesting to note that the plot in Fig. 1 e contains hydrogen bonds between the CO group of Tyr¹ and both the NH group of Gly³ and Phe⁴, which is very different from the hydrogen bonds in plots Fig. 1, a–d.

In another comparison, the lowest-energy configuration obtained in this work for E/3 is similar to the one found in Androulakis et al. (13). We have listed their coordinates in the last column, labeled E/3^(b), in Table 3. There is a difference between the minimal energies obtained from Androulakis et al. (13), E = −11.71 kcal/mol, compared to the present value of E = −12.43 kcal/mol. Our new value, however, is not the indication of a new energy minimum, but a reflection of minor difference in the versions of the force field used. In Androulakis et al. (13), two extra terms, the cysteine loop-closing term and the cysteine torsional term, were included in the potential energy. The conformation also contains a Gly³-Phe⁴ Type-IV β-turn and a Gly³-centered classic γ-turn.

SUMMARY

Using the new basin hopping global optimization method, we have determined the lowest energy minima of Met-enkephalin from four versions of the ECEPP force field, ECEPP/2 and ECEPP/3 with ω relaxed or fixed at 180°. We conclude that the lowest energy minimum configurations of ECEPP/2 and ECEPP/3, with ω relaxed, are virtually identical. With our newly discovered lowest energy minimum for ECEPP/3 with ω fixed at 180°, we also conclude that the minimum configuration of this case shares many common features with those of the other three versions of the force fields; this can be contrasted with an earlier conclusion that the global minimum configuration of this particular case, based on the exactly same version of the parameterization of the force field, is structurally different.