Dynamic Force Spectroscopy of E. coli P Pili

Abstract

Surface organelles (so-called pili) expressed on the bacterial membrane mediate the adhesion of Escherichia coli causing urinary tract infection. These pili possess some extraordinary elongation properties that are assumed to allow a close bacterium-to-host contact even in the presence of shear forces caused by urine flow. The elongation properties of P pili have therefore been assessed for low elongation speeds (steady-state conditions). This work reports on the behavior of P pili probed by dynamic force spectroscopy. A kinetic model for the unfolding of a helixlike chain structure is derived and verified. It is shown that the unfolding of the quaternary structure of the PapA rod takes place at a constant force that is almost independent of elongation speed for slow elongations (up to ∼0.4 μm/s), whereas it shows a dynamic response with a logarithmic dependence for fast elongations. The results provide information about the energy landscape and reaction rates. The bond length and thermal bond opening and closure rates for the layer-to-layer bond have been assessed to ∼0.76 nm, ∼0.8 Hz, and ∼8 GHz, respectively. The results also support a previously constructed sticky-chain model for elongation of the PapA rod that until now had been experimentally verified only under steady-state conditions.

INTRODUCTION

Uropathogenic Escherichia coli (UPEC) are a type of bacteria that commonly are equipped with surface organelles, so called pili, which mediate adhesion to, and interaction with, host tissue. Moreover, P pili are a type of pili that predominantly are expressed by isolates from the upper urinary tract (1,2). They are expressed by ∼90% of the E. coli strains that cause pyelonephritis (severe urinary tract infection) (3). They thereby constitute an important virulence factor. It is therefore of importance to characterize and understand their biophysical properties.

It has previously been shown that the main part of a P pilus constitutes a thin micrometer-long rod, the PapA rod, that has evolved into a three-dimensional helixlike chain structure with a number of unique properties. The PapA rod consists of ∼10³ subunits that are coupled to their nearest neighbors by a β-strand complementation and combined in a right-handed helical arrangement with 3.28 units per turn (4–6) that can be significantly elongated (∼5 times) when exposed to external forces (4,5,7–11).

The fact that UPEC bacteria are implicated in a majority of all urinary tract infections, and that the bacteria in the urinary tract are exposed to mechanical host defenses, primarily urine flows that expose the bacteria to shear forces, suggests that their pili possess some unique elongation properties that presumably are of importance in enabling the bacteria to sustain shear forces and thereby to cause infection. It is clear that bacterial adhesion mediated by several attachment organelles acting in parallel will, if the attachment organelles are stiff, be significantly weaker than the sum of the individual bonds when a bacterium is exposed to shear forces, since the adhesion bonds then will rapidly rupture in a serial mode. On the other hand, if the attachment organelles have a significant degree of flexibility (primarily an ability to elongate under the presence of a force), a given shear force can be distributed among a larger number of attachment organelles, thereby exposing each adhesion bond to a smaller force, even if the bacterium-host distance is widely dissimilar at different parts of the binding area. It has therefore been hypothesized that P pili have evolved into a three-dimensional helixlike chain structure (i.e., the PapA rod) to make it possible for several pili to support tension simultaneously, and thereby for a bacterium to remain attached to the host tissue, in the presence of shear forces/urine flows (5,7–11). This implies that the structure of P pili and their response to external forces are issues of particular importance if the adhesion mechanisms of UPEC bacteria are to be understood and characterized.

This hypothesis of the role of the PapA rod in the bacteria's ability to sustain shear forces has not yet been verified in vivo. On the other hand, various works have been performed throughout the years aiming for a characterization of P pili with regard to their structure as well as various biomechanical properties (4–12). Individual P pili have been characterized with respect to their protein composition and static structure (mainly their size and three-dimensional shape) (4–7). In addition, their biomechanical properties, primarily their elongation response to forces (8), their refolding properties (9), and their long-term stability (11), have been assessed using force-measuring optical tweezers. These studies showed, among other things, that a P pilus has an intricate mode of elongation and unfolding. It elongates in (at least) three regions: a linear region in which the entire organelle is elastically elongated (region I); a region characterized by a constant force in which the helixlike quaternary structure of the PapA rod unfolds to a linear conformation by a sequential rupture of the layer-to-layer bonds (region II); and an “s”-shaped region in which the linearized macromolecule is further elongated by an overstretching of the head-to-tail bond (region III) (8). Most recently, a “sticky-chain” model of the elongation and unfolding of E. coli P pili under strain/stress was developed (10). It was shown that this model provides an accurate description of the elongation behavior of P pili exposed to strain/stress under slow elongation conditions. The work also confirmed that region II is dominated by a cooperative bond opening, in which each bond is influenced by its neighbor, which gives rise to a sequential mode of unfolding, whereas the third region is characterized by an individual bond opening, in which each bond opens and closes randomly, whose force-versus-elongation response is dominated by entropic forces (10). Entities such as the stiffness, the elastic elongation, the opening length of the various bonds, the free energy of the various states, and the number of PapA units in the rod were assessed. The sticky-chain model of the PapA rod has also led to a methodology for a swift determination of the number of PapA units in the PapA rod (12).

All force-elongation studies so far performed were made under slow elongation conditions (so called steady-state conditions), which implies that there is, at each moment, a balance between the bond opening and bond closing rates (8–12). It is well known, however, that the dynamic behavior of biological macromolecules is also of importance for their functioning and that the dynamic response can provide insight into the biophysical properties of a macromolecule (13–21). We have therefore, in this work, investigated the dynamic behavior of the elongation of the PapA rod in P pili of UPEC bacteria by so called dynamic force spectroscopy (DFS) (13–17), using force-measuring optical tweezers instrumentation. Moreover, since it was found that the sequential mode of unfolding of the helical form of the PapA rod (region II) had a significantly more pronounced dynamic behavior than the other regions, the study was focused upon the dynamic behavior of region II. The experiments presented here are the first DFS studies made on E. coli P pili.

Although the dynamic response of a single bond has been described well in the literature (13–17), the dynamic response of a helixlike, chainlike macromolecule, with its unique elongation and unfolding behavior, is not as well understood. However, it can rather easily be concluded, as has been verified by various experiments (8–11,22), that the behavior of the unfolding of a helixlike chain structure that consists of several “layer-to-layer” bonds per turn, which unfolds under constant force by a sequential mode of unfolding, is different from the random opening of a single bond or bonds in a linear chain molecule, which both are well described in the literature (13–17). The unfolding of a helixlike chain structure under a constant force is instead similar to the two-dimensional unzipping of the tertiary structure of λ-DNA that takes place at a constant force (23) or the unzipping of individual β-sheets from amyloid fibrils (24). The main reason to the difference between the opening of a single bond and bonds that open in a sequential mode is the force history of the bond, which previously has been shown to be of major importance for bond breakage (13). Therefore, to evaluate the experimental data, we first derive a simple model that captures the most important dynamic properties of a helixlike chain structure exposed to an elongation at a constant speed along its major axis.

THEORY

Dynamic behavior of the elongation of P pili in region II

As alluded to above, the helical form of the PapA rod, with more than one bond per turn, gives rise to an unfolding of the rod in region II by a sequential opening of the outermost bond when exposed to stress or strain along its major axis. As further discussed below, the sequential mode of unfolding prevents the bond-breaking from taking place at a wide distribution of forces, as is the case for a single bond (13,25,26). The unfolding of a helixlike chain structure, elongated by a constant elongation speed, will instead take place at a virtually constant force, given by the force for which the rate of bond opening, dN_B/dt (where N_B is the number of open layer-to-layer bonds in the PapA rod), is equal to the ratio of the imposed elongation speed of the chain structure, 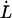, and the bond opening length of a layer-to-layer bond, Δx_AB. It can moreover be argued that the rate of bond opening, dN_B/dt, must, in turn, be equal to the effective opening rate of the outermost bond. Since the effective bond opening rate of a single bond is given by the difference between the bond opening and the bond closure rates, it is possible to conclude that

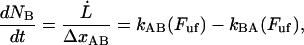(1)

where 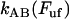and 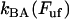are the bond opening and the bond closure rates for a layer-to-layer bond exposed to a force 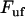, respectively. These two rates can, according to Bell (27), be written as

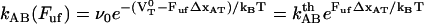(2)

and

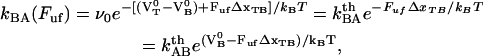(3)

where 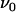is the ordinary attempt rate, 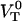and 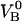the energies of the transition state, 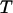, and the ground state of the head-to-tail interaction (state B) that dominates the interaction between the PapA units when the PapA rod is in its linearized conformation, respectively, 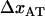and 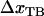the distances between the ground state of the layer-to-layer bond (state A) and the transition state (often referred to as the bond length), and the transition state and state B, respectively, both being positive, 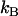and 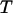Boltzmann's constant and the temperature, respectively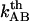, and 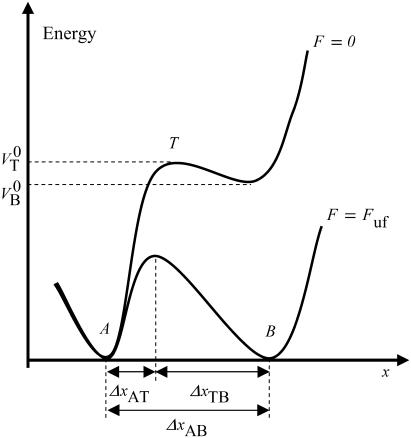and 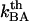the thermal bond opening and closing rates, respectively. Fig. 1 shows a schematic representation of the energy landscape of the layer-to-layer interaction between the various units in the PapA rod as it is elongated along its major axis in which some of these entities are inserted. Equations 2 and 3 illustrate the well known but important fact that whereas the bond opening rate increases with increased force, the bond closing rate decreases. As will be shown below, this is the basis for the dynamic behavior of the unfolding of a helixllike chain structure exposed to strain/stress.

FIGURE 1.

Schematic energy landscape diagram of the interactions between neighboring PapA units elongated along the long axis of the PapA rod (the reaction coordinate, denoted by x). State A represents the closed layer-to-layer bond of the helical structure of the PapA rod, whereas state B symbolizes the head-to-tail interaction that makes up the backbone of the PapA rod. The position of the maximum of the energy landscape curve between states A and B is referred to as the transition state, and is denoted by T. The uppermost curve represents the energy landscape for a PapA rod not exposed to any force, whereas the lower refers to the case when the PapA rod is exposed to a force equal to the unfolding force of the quaternary structure of the PapA rod, 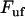. represents the distance from the minimum of state A (in the presence of a force) to the transition state, whereas 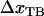is the distance from the transition state to the minimum of state B. 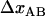represents the total elongation of the layer-to-layer bonds along the reaction coordinate when it opens.

Inserting Eqs. 2 and 3 into Eq. 1 gives a relation between the unfolding force, 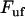, and the elongation speed, 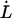, that reads

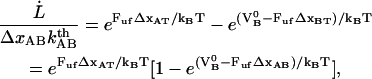(4)

where, in the last step, we have used the fact that the sum of 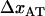and 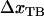is equal to the opening length, .

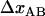This expression has a few important characteristics. The most important is that it shows that the unfolding force of a helically formed chainlike macromolecule does not depend on the loading rate, as that of a single bond does (13,14,16,17); it depends instead on the elongation speed, .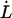

Unfortunately, Eq. 4 cannot be expressed in terms of an analytical function of the form of 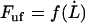. This makes it difficult to directly assess the general force-versus-speed dependence of the unfolding of a helically formed chainlike macromolecule. On the other hand, it is possible to obtain approximate expressions for the unfolding force in various liming situations.

Equation 4 shows, first of all, that the steady-state unfolding rate, 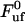, which corresponds to the case when the macromolecule is exposed to a slow elongation, i.e., 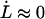, is given by

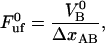(5)

which is an expression that has appeared previously in the literature (10,22). As can be concluded from the equations above, the steady-state unfolding force expressed by Eq. 5 is that for which there is a full balance between the opening (unfolding) and closing (folding) rates, i.e., for which 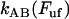= 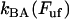. Previous works have shown that the steady-state unfolding force for the PapA rod of P pili takes a value of 27 ± 2 pN (8–10).

Equation 4 shows furthermore that for sufficiently high elongation speeds (those for which the bond opening rate, 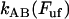, dominates over the bond closing rate, 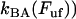, the unfolding rate is related to the elongation speed through a logarithmic dependence, viz., as

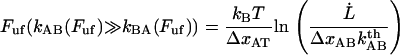(6)

This implies that a plot of the unfolding force versus the logarithm of the elongation speed should, for high elongation speeds, give rise to a straight line whose slope is given by 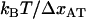. Equation 6 has also previously been discussed in the literature, e.g., regarding the elongation of titin, by Rief et al. (28).

It is also of interest to note that an extrapolation of the logarithmic dependence for high elongation speeds, given by Eq. 6, to lower elongation speeds, provides, by the intercept with the x axis, a value of the thermal bond opening rate, 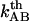, given by

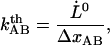(7)

where 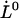denotes the elongation speed at which the extrapolated curve intersects the x axis.

In addition, Eq. 4 shows that the intercept between the horizontal asymptotic line for low elongation speeds, corresponding to 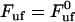, given by Eq. 5, and the asymptotic straight line for high elongation speeds, expressed by Eq. 6, takes place at an elongation speed, denoted by 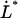and for simplicity referred to as the corner velocity, that is given by

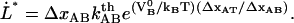(8)

This entity thus represents the elongation velocity that, loosely speaking, separates steady-state conditions from dynamic elongation conditions.

Finally, for intermediate elongation speeds, for which neither of the assumptions for low or high elongation speed are valid, the unfolding force needs to be evaluated by the full expression, Eq. 4. Although this expression cannot be expressed in terms of an analytical function in the form of 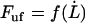, it is possible to derive an expression that relates a given elongation speed to the increase in force above the steady-state force, 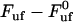, denoted by 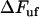, viz.

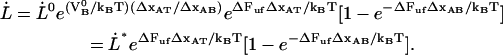(9)

This expression provides not only information about the elongation speed required to increase the unfolding force an amount 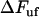, it also shows that is small for all elongation speeds up to the corner velocity, 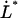. It shows, for example, that the increase in force above the steady-state force at the corner velocity, 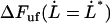, which for short will be denoted by 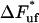, is given by the expression

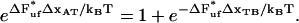(10)

Evaluation procedure for the dynamic behavior of region II

Although experimental data can be fitted directly to Eq. 4, above, it is possible to use the various limiting expressions above to assess separately the most important physical entities for the energy landscape and the bond opening and closure processes of a helixlike chain structure that cannot be determined by the sticky-chain model under steady-state conditions. The slope of the high-elongation-speed asymptote provides, according to Eq. 6, the bond length, 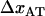. Under the assumption that the bond opening length, 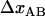, is known, as is the case for the PapA rod (10), this provides directly a value for the distance between the transition state and the ground state of the head-to-tail interaction, 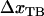. Equation 7 then shows that the intercept of the high-elongation-speed asymptote with the x axis, 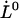, provides a value for the thermal bond opening rate, .

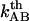With knowledge about these entities, the experimental data can also be used to assess other entities of importance in the biophysical system. Equation 8 shows, for example, that the data also can provide a value for the energy of the head-to-tail bond (state B), 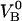(in case this would not be known, or, alternatively, a value based upon an alternative evaluation procedure). This allows, in turn, by the use of Eq. 3, for an assessment of the thermal bond closing rate, 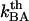. The only model entities that cannot be assessed individually by DFS are the attempt rate, 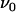, and the energy of the transition state, 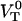, since these two entities always exist in the combination 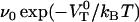. Dynamic force spectroscopy can, however, provide a value for this particular combination of these two entities.

Dynamic behavior of regions I and III

The opening of the head-to-tail bond in region III, which takes place in a random mode, will not experience the same dependence on elongation speed (i.e., dynamic dependence) as the unfolding in region II does. The main reason is that a given elongation of the PapA rod, 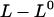, is, in this case, distributed over all N bonds in the PapA rod, and not only the last one that is closed. Since N is ∼10³ for P pili, region III will only be affected by dynamic effects for elongation speeds that are roughly three orders of magnitude larger than those that affect region II. Similarly, because of the helical structure of the PapA rod in its folded configuration, which consists of 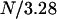layers, it can be argued that region I will also be affected by dynamic effects, only for elongation speeds that are significantly larger (about two to three orders of magnitude) than those that affect region II. This study has therefore been focused on the dynamic effects of region II.

The width of the distribution of rupture forces in region II

In contrast to single-bond force spectroscopy, which shows a distribution of measured rupture forces with a width roughly equal to the value itself (13,15,17), the unfolding of a helixlike chain structure that proceeds in a sequential mode proceeds at a more or less constant force with a narrow force distribution. The reason can qualitatively be attributed to the force history of the outermost bond, which previously has been shown to be of major importance for bond rupture (26).

In short, a single bond exposed to a constant elongation speed is exposed to a steadily increasing force with time, given by the loading rate of the system (which is equal to the product of the elongation speed and the effective stiffness of the system, 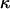, comprising the biological system/macromolecule and the trap) that successively lowers the energy of the transition state and increases the probability of bond opening (27). Since the opening of a bond is a random process, a single bond can rupture under forces either smaller or larger than the average rupture force (which often is referred to as the bond strength). This gives rise to a distribution of rupture forces that has a width in a force histogram that is similar to the bond strength (15,17).

In contrast, a bond in a helixlike chain structure with more than one bond per turn that opens in a sequential mode of unfolding, experiences a fast (more or less immediate) increase in force as its outer neighboring bond opens; from 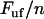(where 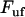is the force at which the neighboring bond opens and 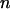the number of bonds per turn), to 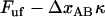(which, according the discussion below, is only marginally lower than that at which the previous bond opened 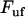). This sudden raise in force increases rapidly the opening rate for the bond from a low (virtually insignificant) level to such a level that the bond immediately experiences a significant probability of opening. This does not give the bond any notable possibility to open at a force lower than 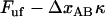, which, in turn, prevents large, sudden drops of force during the sequential mode of unfolding.

When the outer neighboring bond has opened, the bond opening rate for the next bond becomes, in fact, directly so large that it opens reasonably fast; on the average within a time, 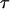, given by the inverse of the bond opening rate of the PapA rod, i.e., 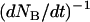. This implies that the bond will open, on the average, when the force has increased an amount given by 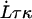. Since 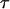is equal to 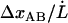, according to the discussion above, the increase in force can also be written as 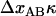. Since the stiffness of the P pili is at least a few times larger than that of the trap, the effective stiffness of the system is given by the stiffness of the trap. With a trap stiffness of 0.14 pN/nm and a bond opening length of 3.5 nm (10), the layer-to-layer bonds in the PapA rod should open, on the average, when the force has increased ∼0.5 pN.

Moreover, since the opening process is a random process, the spread in opening time, 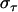, is similar to the average opening time, 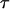. This implies that the spread in the unfolding force, 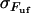, is in the order of 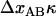(thus, in this case, ∼0.5 pN). Not only does this behavior, on the average, bring the force back up to the unfolding force of the previous bond, 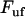, before the bond breaks, it also prevents large positive excursions of the force during the sequential mode of unfolding. This unfolding mechanism is, in fact, a self-regulating process that keeps the unfolding force clamped closely around the average unfolding force, which in general is given by Eq. 4, and thus independent of the stiffness of the system. It is finally worth noting that 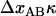constitutes a lower limit as well as a rough estimate of the fluctuations of the unfolding force.

MATERIALS AND METHODS

Biological assay

Individual bacteria (HB101/pPAP5) were mounted on 9.0-μm beads according to the procedure described below. To facilitate mounting of the bacteria, the beads were functionalized with Poly-L-Lysine as follows. Diluted beads were dropped on a coverglass and put in an oven for 55 min at 50°C for firm attachment. A mixture of 0.02 mg/250 ml Poly-L-Lysine was solved in MilliQ water. The solution was then dropped on the dried coverglass and placed in an incubator for 60 min at 37°C. The slides were then gently washed with water and stored at room temperature.

The culture conditions for maintenance of the bacteria have been described elsewhere (29). A typical sample volume (30 μL) for a measurement consists of PBS (pH 7.4), 9.0-μm hydrophobic beads, and 3.2-μm receptor-coated beads and diluted bacteria.

Optical tweezers

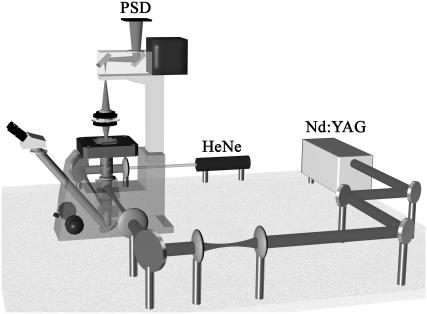
The optical tweezers instrumentation used in this work, schematically shown in Fig. 2, constitutes a set-up built upon the same principles and with the same basic components as those described by Andersson et al. (11). In short, an inverted microscope (Olympus IX71) modified for focusing laser light by a high numerical objective (Olympus, Model UPlanFl 100×/1.30 Oil Immersion) was used. The laser used for trapping was a 10-W continuous-wave 1064-nm Nd:YAG laser (Millennia IR10, Spectra-Physics, Mountain View, CA), run during force measurements with an output power of 1.0 W (measured at the exit port of the laser), giving rise to ∼100 mW in the sample. This amount of laser power gives rise to a temperature increase of ∼1°C in the focus (30), which has a negligible effect on the force calibration and the measurements in this work. This laser power provided a trap with a stiffness of ∼140 pN/μm and a linear measurement range of ±100 pN. An optical-fiber-coupled (SMJ-A3A, 3AF-633-4/125-3-1, OZ Optics, Ottawa, Ontario, Canada) linearly polarized HeNe laser (1137, Uniphase, Manteca, CA) was used for monitoring the position of the trapped bead in combination with a position-sensitive detector. The position-sensitive detector signals were sampled with a data acquisition card (PCI 6259M, National Instru-ments, Austin, TX) in a PC computer with a sampling rate of 5 kHz. The detector signals were filtered by a 2.5 kHz analog low-pass filter (SR640, Stanford Research Systems, Sunnyvale, CA) before digitalization to avoid aliasing effects.

FIGURE 2.

A schematic illustration of the force-measuring optical tweezers setup. A continuous-wave Nd:YAG laser is used for trapping. The trapping position is controlled by a set of lenses and mirrors. The light is introduced via a dichroic mirror coated for high reflection of 1064 nm light and high transmission of visible light. The probe-laser light is produced by a fiber-coupled HeNe laser focused in the proximity of the trapped bead and imaged by the microscope condenser onto a position-sensitive detector (PSD). The sample is placed on a custom-made slide holder mounted in a piezo stage. A detailed description is given in Andersson et al. (11).

Low-frequency noise and drifts that normally limit sensitive force measurements were significantly reduced by placing the optical tweezers instrumentation on an air-damped optical table in a temperature-stabilized room that is isolated from sound and the ventilation system. Noisy electronic instrumentation, e.g., computers and drivers, were placed in adjacent rooms.

Measurement procedure

The following measurement procedure was applied. A free-floating bacterium was trapped by the optical tweezers with reduced power and mounted on a large bead, which was immobilized to the coverslip by the method described above. A small bead was subsequently trapped by the optical tweezers with normal power, brought to a position close to the bacterium and aligned with the large bead and bacterium. A force-measuring calibration procedure based upon Brownian motion, as described elsewhere (29), was used to calibrate the stiffness of the trap before each new set of measurements.

The small bead was brought in contact with the bacterium, the data acquisition was started, and the piezo stage was set in motion to separate the bacterium from the small bead. It was generally found that the bead was attached to the bacterium by several pili. As the separation increased, the pili detached from the bead one at a time. The separation continued, therefore, until a single pilus response was present. The stage was then reversed and stopped while the remaining pilus still was in region II. A start and a stop position for repetitive elongations in region II were defined (typically with a separation of 2–3 μm). The remaining pilus was then elongated repeated times between the start and the stop positions with a given elongation speed by a custom made computer program that controlled the traveling and the speed at which the stage was moved. After each forward motion, the stage was reversed with a low speed to allow refolding of the PapA rod.

RESULTS

Qualitative assessment of DFS of P pili

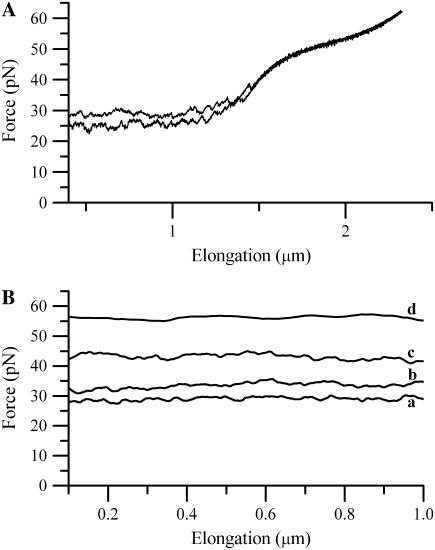
As was mentioned above, the force-versus-elongation re-sponse of a single P pilus under steady-state conditions has previously been investigated in some detail (8–12). Typical single-pilus steady-state response curves, as well as control measurements (assessing irrefutably the measured response to individual pili, and not, for example, to the bacterial cell or its membrane), can therefore be found in the literature (8–10). Fig. 3 A shows the force-versus-elongation response of the last part of region II and the first part of region III from an individual P pilus for two dissimilar elongation velocities. The lower curve represents the response of a P pilus elongated under such a low elongation speed (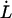 = 0.2 μm/s) that its response is close to that at steady state. The upper curve shows the response of a pilus for a larger elongation speed (0.8 μm/s), for which dynamic effects start to play a role. Fig. 3 A shows clearly that the main effect of an in-creased elongation speed is an increase of the unfolding force in region II, whereas the force in region III is unaffected by the increase in elongation speed, which is in good agreement with the discussion given above. The remaining part of this study was therefore directed to the dynamic response of region II.

FIGURE 3.

(A) A force-versus-elongation response of the last part of region II and the first part of region III from an individual E. coli P pilus for two dissimilar elongation velocities: lower curve, 0.2 μm/s; and upper curve, 0.8 μm/s. (B) The dynamic response of the unfolding of the quaternary structure of the PapA rod in region II for four different elongation speeds: a, 0.1 μm/s; b, 0.75 μm/s; c, 5.7 μm/s; and d, 42.7 μm/s. The data in B have been subjected to a moving-average filtering for clarity.

Several series of measurements (>25) of the dynamic response of the elongation of individual P pili in region II, each comprising an investigation of a given P pilus under a variety of elongation speeds, were performed. Experiments were made for a range of velocities ranging from 0.05 to 120 μm/s, for which the unfolding force was found to vary between 27 and 65 pN. Fig. 3 B shows, as an example, the dynamic response of a part of region II from measurements of the unfolding of the PapA rod of an individual E. coli P pilus for four different elongation speeds (0.1, 0.75, 5.7, and 43 μm/s, respectively). As can be seen from the figure, for a given elongation speed the force is rather constant (except for some random noise), i.e., independent of the elongation. The level of the force depends, however, on the elongation speed (in this case with forces levels of 29, 34, 43, and 55 pN, respectively), which is in qualitative agreement with the behavior predicted by the theoretical description given above.

The width of the distribution of rupture forces in region II

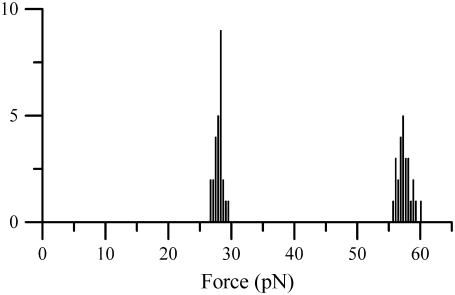
The distribution of unfolding forces is illustrated in Fig. 4, which shows a histogram of the unfolding force of region II of P pili from a number of consecutive measurements at two different elongation speeds, 0.1 and 50 μm/s, respectively (which gave rise to mean unfolding forces of 28.1 and 57.4 pN, respectively). The plot shows clearly, in agreement with the discussion above, a small spread in unfolding force, 0.7 and 1.1 pN for the two elongation speeds, respectively, which is in reasonable agreement with the discussion above and in clear contrast to that of a single bond (26). These spreads in force value represent the combined spread due to the bond opening process of the PapA rod and noise from the measurement system and therefore do not necessarily indicate the true spread in the bond opening process of the PapA rod. As has been discussed previously, the small spread is therefore also an indication of the stability of the force-measuring system (11).

FIGURE 4.

A histogram of the unfolding force of the PapA rod for a number of unfoldings for two different elongation speeds: 0.1 and 50 μm/s, respectively. The two elongation speeds gave rise to unfolding forces of 28.1 ± 0.7 pN and 57.4 ±1.1 pN and widths of 0.7 pN and 1.1 pN, respectively.

Quantitative assessment of DFS of P pili and relevant model parameters

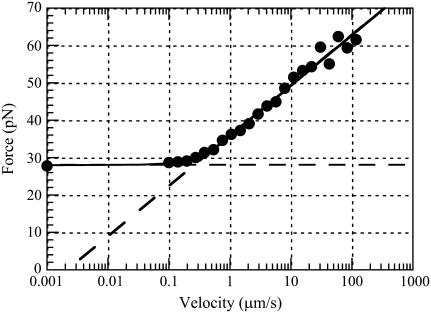
Fig. 5 shows an example of a series of DFS measurement performed on a single P pilus. Each data point represents the unfolding force of the P pilus at a given elongation speed. Measurements were in this particular case performed for elongation speeds ranging from 0.1 to 117 μm/s. The data point at 0.001 μm/s represents the force measured when the pilus was held at a fixed elongation length (i.e., for a speed of zero), and it has been inserted in the figure at this position for illustrative purposes.

FIGURE 5.

Unfolding force in region II of a single P pilus versus elongation speed. The solid curve represents a fit of Eq. 4 to the data, whereas the dashed lines represent the low- and high-elongation-speed asymptotes, given by Eqs. 5 and 6, respectively. The intercept of the two asymptotes represents the corner frequency, 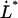, whereas the intercept of the high-elongation-speed asymptote with the x axis gives 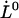, which in turn provides a value for the thermal bond opening rate,.

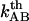The solid curve represents a fit of Eq. 4 to the data, whereas the dashed lines represent the low- and high-elongation-speed asymptotes, given by Eqs. 5 and 6, respectively. As can be seen from the figure, the agreement between the fits and the data points is good. This particular data set provided the following values of the entities discussed in the theory section above: 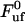= 28 pN, 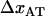= 0.70 nm, 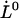= 0.0022 μm/s and 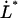= 0.25 μm/s. Other series of measurements, each for its own P pilus, provide similar sets of data, with comparably good fits. The average values of these entities over all sets of data were found to be 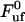= 28 ± 2 pN, 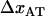= 0.76 ± 0.11 nm, 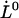= 0.0029 ± 0.0018 μm/s, and 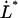= 0.39 ± 0.14 μm/s.

DISCUSSION

A value of the steady-state unfolding force of 28 ± 2 pN is in good agreement with the results previously obtained under steady-state conditions (27 ± 2 pN) (8–10). This implies that also the previously determined values of the energy of the ground state of the head-to-tail interaction (state B), 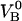, of 23 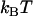± 1 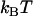, and the bond opening length, 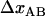, of 3.5 ± 0.1 nm, can be considered to be trustworthy (10). The assessment of 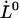can therefore be used to provide a value of the thermal bond opening rate of the layer-to-layer bond, 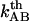through Eq. 7, and thereby also 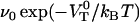, of 0.8 ± 0.5 Hz.

A thermal bond opening of 0.8 ± 0.5 Hz is in reasonable agreement with thermal bond opening rates of other types of bonds, which have been found to be in the 1–10 Hz range (20,31,32). It indicates, in turn, by Eq. 3, that the thermal bond closure rate, 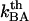, is in the range 3 × 10⁹–13 × 10⁹ Hz. Since 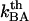is several orders of magnitude larger than 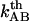, this first supports the assumption that any spontaneously opened bond will, in the absence of applied force, directly refold. 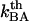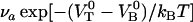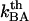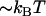Moreover, since the bond closing rate also can be expressed in terms of the attempt rate and the difference between the energy of the transition state and state B as = and the attempt rate is in general in the order of 10⁹–10¹⁰ Hz (27), a value of of 3 × 10⁹–13 × 10⁹ Hz implies either that the B state constitutes a shallow minimum in the energy landscape (e.g., takes a value of only for a 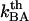of ∼3 × 10⁹ Hz and an attempt rate of 10¹⁰ Hz) or that it is, in fact, not even a bound state in the absence of force. This implies that the schematic representation of the energy landscape in the absence of a force provided by the upper curve in Fig. 1 might be slightly misleading. This does not, however, affect the validity of the model or any of the other conclusions, since the B state will develop into a bound state in the presence of an external force.

In addition, with knowledge about the thermal bond opening rate (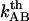) of 0.8 ± 0.5 Hz, the steady-state unfolding force (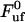) of 27 ± 2 pN, and the bond length in the presence of an unfolding force (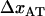) of 0.76 ± 0.11 nm, it is possible, by the use of Eq. 2, to estimate the bond opening rate (and thereby the bond closing rate) for the layer-to-layer bond in region II under steady-state conditions. It is found that 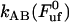= = 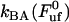120 ± 75 Hz.

Moreover, a value of the bond length in the presence of an unfolding force () of 0.76 ± 0.11 nm implies that the distance between the transition state and state B, 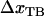, is 2.8 ± 0.2 nm, which in turn indicates, according to Eq. 10, that the force is expected to increase ∼1.6 pN above the steady-state force at the corner velocity, which, according to Fig. 5, also is in good agreement with the experimental findings.

A bond length of ∼0.76 ± 0.11 nm is also in reasonable agreement with other bond lengths of biological macromolecules, which, however, have been found to vary widely (21,31). For example, Merkel et al., who performed dynamic force spectroscopy on streptavidin and avidin interacting with biotin, found prominent barriers of ligand-receptor bonds at several locations; a first sharp inner barrier at 0.12 nm, followed by a second barrier at 0.3 nm for avidin and 0.5 nm for streptavidin (16). Moreover, Evans reported on barriers in carbohydrate-L-selectin linkages at 0.06, 0.3, and 1.2 nm (15).

The good agreement between the experimental data and the theoretical model shows, first of all, that the model is adequate. The dynamic response also indicates clearly that there is only one single energy barrier between the states representing a folded and an unfolded layer-to-layer bond. Various physical parameters describing the energy landscape, transition distances, and function of P pili exposed to dynamic forces have been assessed. The most important are: the bond length in the presence of an unfolding force, 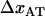, which was assessed to 0.76 ± 0.11 nm; the corner velocity, 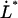(which constitutes the elongation velocity that separates steady-state from dynamic behavior), which was found to be 0.4 μm/s; and the bond opening rate for the layer-to-layer bond under steady-state conditions, 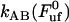, which was found to be 120 ± 75 Hz. The data also suggest that the B state is very shallow, or not even bound, in the absence of forces. This does not prevent the PapA rod from unfolding under the presence of an external force, since the B state, in such a case, rapidly develops into a bound state.

A bacterium that binds to epithelial cells in the urinary tract is exposed to shear forces from urine flow and is presumably attached by several pili simultaneously. It is therefore not trivial to correctly correlate the behavior of E. coli in vivo to the behavior of a single pilus exposed to a given stress or strain. Instead, it is only by first properly assessing the mechanical and biophysical properties of an individual P pilus exposed to an external force under well-specified conditions, including the specific adhesion strength of the PapG adhesin as well as the collective behavior of several pili binding simultaneously, that we can understand, in a quantitative manner, the binding of an individual bacterium to epithelial cells in vivo. We do not yet have a complete model of the collective behavior of several pili exposed to stress or strain or knowledge about the adhesion strength, nor do we know how many pili a given bacterium in vivo binds with in a given situation. This DFS study was therefore primarily performed to complement previous investigations concerned with assessments of various mechanical and biophysical properties of individual P pili (8–10).

The results of this study regarding the dynamic properties of individual pili are nevertheless in good agreement with previous findings of similar bacterial systems. For example, Nilsson et al. (33) have shown that E. coli expressing type 1 pili can sustain wall shear stress of at least 4 pN/μm² without detaching from a mannose surface. Using Goldman's approximation for the force to which a spherical particle tethered to a surface is exposed by a given shear stress, and assuming that the bacterium is spherical and has a size of 1 μm, it can be estimated that this wall shear stress corresponds to a total drag force of 130 pN; a force level which can be seen to reflect physiological conditions in vivo (34). However, the bacterial system of Nilsson et al. involved an unknown number of pili binding simultaneously, wherefore no direct comparison between our single-pilus findings and those of Nilsson et al. can be made. On the other hand, since the cooperative drag force of 130 pN is larger than the unfolding force of an individual pilus in this as well as in our previous studies (27 pN under steady-state conditions and up to 60 pN under dynamic conditions (8-12)), the results presented here are in good agreement with the above estimate of the in vivo conditions. Moreover, the range of velocities studied in this work, up to ∼100 μm/s, is also in good agreement with conditions bacteria showing a rolling behavior can experience in vivo (such bacteria have been found to move with a speed of around 30 μm/s) (34). This study therefore indicates that a single pilus of a bacterium showing a rolling behavior suddenly attaching to a surface will give rise to a retracting force of ∼50–60 pN while unfolding.

SUMMARY

The dynamic response of the unfolding of E. coli P pili by the use of dynamic force spectroscopy using optical tweezers has been investigated. It was found that for the range of elongation velocities studied, 0.05 to 120 μm/s, region II, in which the helical (quaternary) structure of the PapA rod unfolds in a sequential mode, showed a clear dynamic response (the unfolding force ranged from 27 to 65 pN), whereas the other regions did not. The study was therefore focused upon region II.

A theoretical model for the unfolding of a helixlike chain structure with more than one layer-to-layer bond per turn has been developed and applied to the unfolding of the PapA rod of E. coli P pili. The agreement between the experimental findings and the theoretical model was found to be good. It was furthermore found that the unfolding force, which is independent of the number of units in the PapA rod and constant for a given elongation speed, was virtually independent of the elongation speed for the slowest elongations (below a velocity referred to as the corner velocity), but that it increases successively with elongation speed, and shows a logarithmic dependence on the elongation speed for large elongation speeds (above the corner velocity).