Abstract
A model for the calculation of amide I FTIR and 2DIR spectra taking into account fluctuations in hydrogen bonding and structure from molecular dynamics (MD) simulations is tested on three systems. It is found that although the homogeneous lineshape approximation yields satisfactory FTIR spectra, 2DIR spectra are sensitive to the inhomogeneity naturally present in any solvated protein and the common approximations of a static structure and averaged-effect solvent are invalid. By building on the local amide Hamiltonian and incorporating site energy variation with electrostatic-based models and disorder from MD trajectories, good agreement is obtained between calculated and measured 2DIR spectra. The largest contribution to the observed inhomogeneity is found to be the fluctuating site energies, which in turn are most sensitive to the water solvent. With the ability to accurately predict 2DIR spectra from atomistic simulations, new opportunities to test force fields and mechanistic predictions from MD are revealed.
INTRODUCTION
Amide I is the backbone CO stretching region of a protein infrared spectrum (1600–1700 cm−1). Its large transition dipole moment (∼4 D Å−1 amu−1/2 per oscillator) (1) both makes it the strongest feature in a protein infrared spectrum and causes the eigenstates to be delocalized by long-range electrostatic coupling. As a result of this delocalization and the inherent fast time resolution of infrared spectroscopy, the amide I lineshape of proteins and peptides has been used as both a rough structural analysis tool and a fast dynamic probe of protein secondary structure. Yet, the amide I lineshape has been difficult to model on the basis of protein structure in a way that incorporates structural plasticity and fluctuating hydrogen bonds.
The amide I region contains roughly as many eigenstates as there are peptide linkages, but with a natural linewidth of ∼10 cm−1 (2,3), spectra become congested very quickly with increasing peptide size. This dense set of states is sensitive to many intramolecular structural variables as well as intermolecular solvation forces, all evolving on timescales from tens of femtoseconds to nanoseconds, and so the observed FTIR lineshape is broad with few features—typically one pronounced peak and perhaps a shoulder. This mismatch between input parameters and observables has made it difficult to understand the relative importance of coupling and solvent effects. Thus, amide I FTIR of proteins has largely been constrained to group frequency interpretations or unphysically motivated Fourier band deconvolution (4–6), except in the case of very small peptides (7).
The first observation of the structural sensitivity of amide I (8), namely that α-helical systems peak ∼20 cm−1 higher in energy than β-sheet systems, led to theories attributing the difference in frequency to local hydrogen-bonding environment (9) and strong coupling (10). Subsequent work answered the original question with the conceptually simple transition dipole coupling model (11), but studies of N-methylacetamide (NMA) in different hydrogen bonding motifs (12–16) showed that both are important. An empirical correction to the amide I frequency of NMA due to hydrogen bonding was proposed and widely used (2). The observation that the frequency shift is additive with increasing hydrogen-bonding partners (15) suggested a purely electrostatic cause with negligible effects of induction, covalency, or dispersion, and led to the development of several more accurate electrostatic models correlating the amide I frequency with the potential or electric field at the amide atomic sites (17–21). This conveniently suggests a concerted treatment of molecular dynamics (MD) and amide I IR spectroscopy calculation, as the forces and structural variations from MD are direct parameters in an imposed spectroscopic Hamiltonian. This ability to calculate observables from MD simulations provides an important link and test of the wealth of dynamical information from MD that has gone largely untested—most of the tests of MD simulations are thermodynamic (binding and folding free energies), kinetic (rate constants), or structural (comparison to x-ray or NMR structures), rather than mechanistic. Where coherent reaction initiation is possible, transient spectra can be measured and calculated from nonequilibrium MD trajectories, providing a rigorous test of the predicted mechanism.
The recent developments in two-dimensional infrared spectroscopy (2DIR) allow a new understanding of the amide I lineshape based on its ability to distinguish between natural line widths and heterogeneous ensembles and the appearance of structurally sensitive cross peaks. It will be shown that the approximations sufficient to yield good agreement in calculated FTIR spectra predict 2DIR lineshapes that disagree with experiment. This is because the 2DIR spectrum contains additional information; inhomogeneous broadening appears as a diagonal (ω1 = ω3) elongation of the lineshapes and correlated energy shifts between any two eigenstates A (ωA) and B (ωB) are revealed in the A-B cross peak shape at (ωA, ωB) and (ωB, ωA) (22). Thus, it is possible in FTIR, but not 2DIR, to use unphysically broad homogeneous lineshapes to mask a lack of knowledge of the correct inhomogeneous broadening in the system. This sensitivity of 2DIR to ensemble heterogeneity provides a rigorous test of equilibrium MD trajectories to correctly sample disorder in the system. There is a lot of interest on this front and other researchers are also pursuing structure-based models of FTIR and 2DIR spectra from MD simulations (23–25).
It is our goal in this work to test a model with no fitting of IR spectra for calculating the amide I lineshape that is consistent with both observed FTIR and 2DIR data. The only external parameters that enter are obtained from other IR experiments or MD simulations. We work within the established framework of a subspace of amide I local modes (2) and evaluate site energy models with MD simulations to incorporate fluctuations in the solute and solvent. We demonstrate the modeling with three test systems that survey different secondary structure motifs—a 12-residue β-hairpin (trpzip2), a 19-residue α-helix (D-Arg), and a 76-residue α + β protein (ubiquitin). We find that including electrostatic contributions from the solvent, side chains, and backbone residues are important in establishing the correct red-shift to the overall amide I band position. We find that disorder in the site energies, but not couplings, are critical for experimental agreement with calculated 2DIR spectra, which implies that disorder in site energies is critical for calculating physically meaningful FTIR spectra. These methods, despite the approximations made, yield good results with lineshapes slightly broader than observed. Systematic improvements are also suggested.
METHODS
The amide I subspace
The main simplifying assumption that allows calculation of the amide I lineshape is the description of amide I eigenstates as linear combinations of local amide I vibrations, which ensures that for a polypeptide comprised of (N + 1) amino acids and N peptide groups, there will only be N relevant local modes to consider. This is valid insomuch as the local amide I vibration is localized to a single backbone unit and was first introduced by Miyazawa (10) with important contributions from Krimm (26,27) and Torii and Tasumi (1,15,28), who used the GF matrix formalism. This local amide I Hamiltonian picture showed that the FTIR lineshape could be well approximated by considering local oscillator force constants (diagonal elements) and coupling between local oscillators (off-diagonal elements) without considering side chains, solvent, or disorder. Because the G matrix is diagonal, an isomorphic representation is to directly consider parameters of the Hamiltonian in units of cm−1, an approach that was suggested with the excitonic modeling of 2DIR spectra by Hamm and Hochstrasser (2,29) and subsequently expanded. We follow this approach, which means that our site energies (diagonal elements) reflect both the local oscillator force constant and reduced mass.
Site-energy models
We considered 10 different site-energy models. Eight of these models are based on electrostatics and their salient features are summarized in Table 1. We also consider two other models: the degenerate case (all sites = 1650 cm−1), which was the starting point for Torii and Tasumi's work on globular proteins (1), and an empirical heuristic site-energy model based on probable hydrogen bonds (30) from the crystal structure. For simplicity at this point, we ignore nonelectrostatic contributions to the site energy (31). We find that many field and potential models compare favorably with one another and so we choose results from four of the 10 site energy models to plot and the rest are included in the Supplementary Material. In each of the electrostatic models, the site energy for each peptide group, I, was parameterized by correlation of the calculated amide I frequency to the electrostatic environment evaluated at n various sites i (typically C, O, N, D) in N-methylacetamide (NMA). We calculate the electrostatic environment by considering the protein-solvent system as a cluster of point partial charges perturbing one amide group. In the most general form, the electrostatic models we study define the amide I frequency for site I, ωI, as
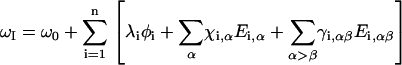 |
(1) |
The site energy is linearly proportional to the scalar electrostatic potential,
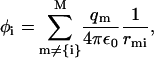 |
(2) |
the vector electric field,
 |
(3) |
and the tensorial gradient of the electric field,
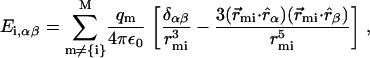 |
(4) |
from all atoms m outside the peptide group. A site-energy model is defined by the included terms in Eq. 1 and the correlation coefficients λu, χu, and γu that dictate frequency shifts and the initial ω0, which is typically the gas phase value but may be parameterized to include a static shift (17,18,20). In Eqs. 1, 3, and 4, Greek indices run over the amide group space (α, β ∈ {x, y, z}). The CO bond of each amide group defines a y axis. The x axis is perpendicular to the y axis and points toward the amide N, in the CON plane, and 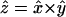 . Although all of these electrostatic site-energy models are acausal by construction, that is, the electrostatics of an amide group are fit to a frequency shift without reference to the underlying mechanism, the coefficients λu, χu, and γu can be understood as vibrational Stark tuning rates (32,33). In analogy to work on HOD/D2O where
. Although all of these electrostatic site-energy models are acausal by construction, that is, the electrostatics of an amide group are fit to a frequency shift without reference to the underlying mechanism, the coefficients λu, χu, and γu can be understood as vibrational Stark tuning rates (32,33). In analogy to work on HOD/D2O where 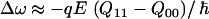 (34), the coefficient for each atom can be roughly identified as a measure of the partial charge, times the mean displacement in amide I.
(34), the coefficient for each atom can be roughly identified as a measure of the partial charge, times the mean displacement in amide I.
TABLE 1.
Site energy models and fluctuation statistics for Trpzip2
| Property correlated | Model name | Parameterized sites (m) | 〈ω〉 | 〈σ〉 | 〈δωWater〉 | 〈δωBackbone〉 | 〈δωSidechain〉 |
|---|---|---|---|---|---|---|---|
| Potential | Keiderling 5P (19) | Cα C O N D | 1660 | 16.6 | −27.5 | −15.8 | −13.2 |
| Potential | Cho 6P* (18) | Cα C O N H Cα | 1649 | 15.6 | −28.6 | −17.7 | −11.0 |
| Potential | Cho 4P* (17) | C O N H | 1657 | 15.2 | −26.0 | −13.4 | −10.3 |
| Potential | Hirst 7P (66) | C COmid O CNmid N NHmid H | 1686 | 14.7 | −12.3 | −9.3 | −8.9 |
| Potential | Hirst 4P* (66) | C O N H | 1696 | 7.1 | −9.9 | −6.5 | −4.4 |
| Potential | Skinner 6P* (20) | Cα C O N D Cα | 1660 | 17.4 | −24.6 | −19.2 | −12.8 |
| Field | Skinner 6F* (20) | Cα C O N D Cα | 1675 | 24.2 | −18.3 | −2.0 | −14.5 |
| Field to 2nd order | Jansen 4F (21) | C O N D | 1670 | 24.8 | −26.3 | −1.9 | −18.5 |
Listing of site-energy models tested, comparison of electrostatic property-correlated, site-correlated, nomenclature, and fluctuation statistics for Trpzip2. The value 〈ω〉 is the average site frequency, which is broken down to contributions from water, backbone, and side chain, respectively, in 〈δωWater〉, 〈δωBackbone〉, and 〈δωSidechain〉. The value 〈σ〉 is the average site standard deviation. All quantities are in cm−1.
Spectra appear in the Supplementary Material.
In the parameterization of these site-energy models, the electrostatics of the solvent are correlated to the amide I frequency of NMA, not to a peptide group in a protein. We extend the original definition of the solvent to include not only the water, but also the side chains and neighboring backbone and the chromophore to be a peptide group in a chain. The sums over m that define φ and E for a peptide group do not include the nitrogen or α-carbons flanking the carbonyl nor the associated backbone protons. This definition maintains electrostatic neutrality of the system in CHARMM27 and ENCAD force fields, as well as several others.
We also consider a heuristic site-energy model based on structure (30). We start with an average solvated frequency of 1688 cm−1 and apply a set of red-shifting criteria,
 |
(5) |
For backbone hydrogen-bonding on the carbonyl side,
 |
(6) |
where rH–O is the hydrogen-oxygen backbone hydrogen-bond distance (2). For water hydrogen-bonding on the carbonyl side,  . For any hydrogen bond on the amino side, we red-shift by
. For any hydrogen bond on the amino side, we red-shift by  . For no hydrogen bonding,
. For no hydrogen bonding, 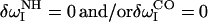 .
.
Coupling Model
Historically, transition dipole coupling was used to explain the splitting of the amide I band observed in β-sheets, but subsequent calculations (35) highlighted the failure of the dipole approximation at short distances and the importance of through-bond effects. In light of this, we use a DFT lookup table (36) for coupling between bonded neighbors, which can be roughly understood as the second derivative of the total calculated electronic energy with respect to local coordinates QI and QJ in a model dipeptide,
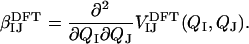 |
(7) |
This implicitly treats the quantum mechanical, through-bond effects most relevant for covalently bonded amide groups as well as electrostatics to all-order. All other interactions are treated with transition charge coupling (17,28,35). The TCC coupling equation represents the interaction energy between a cluster of partial charges on peptide groups I and J as a function of local coordinate displacements, which circumvents the dipole approximation of TDC and includes polarizability effects by allowing the charges to change magnitude. The TCC coupling is defined by
 |
(8) |
where QI is the dimensionless local coordinate,
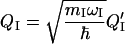 |
(9) |
and q0 and q1 are the parameters from a linear fit to the calculated Mulliken charge at each atomic center as a function of local amide I coordinate displacement on N-methylacetamide, with the methyl hydrogen partial charges summed to the methyl carbons. Calculations to parameterize TCC were carried out using the Gaussian 98 implementation of B3LYP/6-31+G* (37). The transition dipole is obtained by numerical differentiation and found to lie in the NCO plane, 25° off the CO bond axis toward the nitrogen. The magnitude and orientation with respect to the amide group are fixed (21). The index i(j) runs over all atoms of the peptide group I(J).
MD simulations
In the present case, MD simulations are used to generate an ensemble of structures representative of the experiment. With static averaging (or “instantaneous normal modes”), FTIR and 2DIR spectra are summed for each structure in a set representative of the equilibrium ensemble. In a dynamical picture, this corresponds to a slow interconversion of spectroscopically distinct structures on a timescale longer than the experiment (∼2 ps). This approximation leads to artificially broader lineshapes if there are any spectroscopically relevant fast fluctuations. This is undoubtedly the case to some degree as water undergoes many fast motions that can modulate the amide I frequency. However, in the interest of computational and conceptual simplicity, this work operates purely in the static average picture.
We choose three systems to test the generality of the models that span different secondary structure motifs and sizes. Trpzip2 is an extensively studied (38–44) 12-residue peptide that forms a stable, antiparallel β-hairpin in water. D-Arg is a 19-residue alanine-rich α-helical peptide, based loosely on the Marquesee-Baldwin water-soluble α-helical peptide (45,46). In addition to an α-helix and a β-hairpin, we consider a 76-residue α + β protein ubiquitin to test on a realistic protein.
The initial trpzip2 structure is taken from the published solution NMR structures (PDB 1LE1 (41)). MD simulations are carried out in the CHARMM 30b1 package (47). All acidic protons are deuterated to match the experimental conditions. This structure is briefly energy-minimized for 1000 steps in the CHARMM27 force field. Thereafter in the simulation, the bond lengths are constrained with the SHAKE algorithm. The peptide is then placed in the center of a preequilibrated (298 K, 1 g/cc) box of 2048 SPC/E water molecules with periodic, cubic boundary conditions. Waters with oxygens within 2 Å of the peptide are removed. Because at pH 7.0 the peptide has a formal charge of +1, a Cl− counterion was added at a random place in the box. Electrostatics are handled by particle-mesh Ewald sums and VDW interactions are shifted to reach zero at the truncation length of 14 Å. Ten trajectories are spawned from this initial structure with different initial seeds and each equilibrated for 1 ns in the NPT ensemble (Berendsen method, 298 K, 1 atm), which is long enough to allow the water to reorient and let the box length converge. Dynamics are continued in the NPT ensemble and the structures are saved at 20-fs intervals for analysis for 1-ns total of trajectory.
The initial D-Arg structure was constructed assuming the secondary structure generated an ideal helix (repeating φ = −90° and ψ = −45°) for the residues NH3-YGG(KAAAA)3-(D-R)-CONH2, where the Arg is of right-handed chirality. The remaining procedures are identical to trpzip2, except five randomly placed Cl− counterions were added for charge neutrality.
Ubiquitin structures are generated from equilibrium MD performed by Alonso and Daggett (48) and sampled at 300 ps for IR spectral calculations. Spectra were calculated from the protonated structures, assuming that all acidic protons can be deuterated without significantly affecting the dynamics.
IR spectroscopy
From the MD simulation, each (N + 1) residue, solvated protein, or peptide structure defines a vector of N local transition dipole vectors and an N × N Hamiltonian composed from the site energies and couplings as described above in the local amide I basis. Diagonalization of this Hamiltonian yields a set of energies, ωk. The Hamiltonian diagonalization transformation is used to transform the local amide I transition dipoles to the transition dipoles,  .
.
An FTIR stick spectrum for a structure is generated from the eigenstate energies and transition dipoles and then lifetime-broadened and summed over the ensemble,
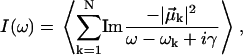 |
(10) |
where 〈 〉 indicates the equilibrium Boltzmann average. Although in some studies the HWHM broadening parameter γ is fit, we set it to 5 cm−1 for all systems corresponding to a lifetime of ∼1 ps (2). Note additionally that inhomogeneous broadening arises naturally by the sum over structures.
In practice, the spectra are summed as stick spectra on a grid of 1 cm−1, then convolved with the Lorentzian lineshape function afterwards for an increase in computational efficiency by avoiding continuous recalculation of identical lineshapes. The two methods are mathematically identical and indistinguishable with the chosen grid spacing:
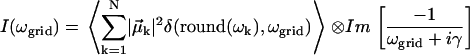 |
(11) |
Two-dimensional infrared spectra are calculated by taking the undiagonalized one-quantum Hamiltonian described above for FTIR, H, and defining a scaled two-quantum Hamiltonian, H(2), to include two-quantum local states and couplings, which is zero unless
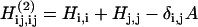 |
(12a) |
 |
(12b) |
 |
(12c) |
where δi, j is the Kronecker Delta symbol, A is the overtone anharmonicity set to 16 cm−1 (2), and the indices commute to 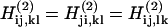 Part of the increased sensitivity of 2DIR is seen in Eq. 12a; the two-quantum Hamiltonian is sensitive to correlations in frequency shifts of the fundamental frequencies in a manner that is difficult to guess a priori.
Part of the increased sensitivity of 2DIR is seen in Eq. 12a; the two-quantum Hamiltonian is sensitive to correlations in frequency shifts of the fundamental frequencies in a manner that is difficult to guess a priori.
The local transition dipoles are also harmonically scaled to produce two-quantum transition dipoles,
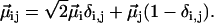 |
(13) |
The two-quantum Hamiltonian is diagonalized to yield a set of (N2 + N)/2 energies,  , which are used to transform the local transition dipoles and calculate the ZZYY (first two light fields are perpendicularly polarized to the third and detection) rephasing, S1, and nonrephasing, S2, signals (49), which when summed yield the purely absorptive 2DIR spectra. In a manner completely analogous to the FTIR, the rephasing and nonrephasing signals are summed independently as stick spectra, then convolved with the appropriate lineshape functions and summed to yield the 2DIR correlation spectrum. Details are available in the Supplementary Material.
, which are used to transform the local transition dipoles and calculate the ZZYY (first two light fields are perpendicularly polarized to the third and detection) rephasing, S1, and nonrephasing, S2, signals (49), which when summed yield the purely absorptive 2DIR spectra. In a manner completely analogous to the FTIR, the rephasing and nonrephasing signals are summed independently as stick spectra, then convolved with the appropriate lineshape functions and summed to yield the 2DIR correlation spectrum. Details are available in the Supplementary Material.
Experimental
The experimental methods employed here are identical to those described previously (38,50). Trpzip2 (SWTWENGKWTWK) and D-Arg (45) (YGG(KAAAA)3-(D-R), where the Arg is of right-handed chirality, were synthesized at the MIT Biopolymers Lab (Cambridge, MA) using Fmoc solid-phase synthesis as C-terminal amide peptides, HPLC-purified, then lyophilized against 50 mM DCl to remove residual trifluoroacetic acid. The α-helical character of D-Arg was verified with UVCD (data not shown). BPTI (structure from PDB 1BPI (51)) was purchased from Sigma (St. Louis, MO) and used without further purification.
RESULTS AND DISCUSSION
Information content of FTIR versus 2DIR
The increased information content of 2DIR can be used to confirm or reject approximations made in calculating the amide I FTIR lineshape. In Fig. 1, we show the calculated FTIR and 2DIR spectra for the protein BPTI using the heuristic site-energy model based on one crystal structure (1BPI (51)) with several values of the homogeneous broadening parameter, γ, and no inhomogeneous broadening. By comparing the bandshapes, it can be seen that a value of γ ≈ 16 cm−1 reproduces the shoulder and FWHM of the observed FTIR shape. However, the 2DIR spectrum implied by this homogeneous broadening is qualitatively very different than the observed 2DIR. The measured 2DIR lineshapes are diagonally elongated, a signature of inhomogeneity in the system.
FIGURE 1.
As the Lorentzian HWHM parameter γ is increased, the predicted FTIR linewidth begins to match experiment, but the predicted tilt in the 2DIR peaks is qualitatively incorrect. The spectra are for bovine pancreatic trypsin inhibitor (BPTI) calculated using the heuristic site-energy model from the PDB structure 1BPI (51). Twenty-one evenly spaced contours are plotted from ±50% of the maximum for each spectrum.
It can be seen in the calculations that when an unphysically narrow linewidth eliminates crowding (γ = 3 cm−1), many distinct off-diagonal cross peaks compose the observed lineshapes. For example, a series of cross-peaks extending in the +ω3 and +ω1 direction from the ∼1650 cm−1 fundamental peak arises from anharmonic coupling between these vibrations.
In the homogeneous limit, these cross peaks are round. In the presence of inhomogeneity, correlated frequency shifts between the ∼1650 cm−1 peak and any of these other peaks will be reflected in the cross-peak shape. For example, a change in the angle between hydrogen-bonded peptide groups will modulate the coupling and can cause a correlated red- and blue-shift in a doublet of peaks. Water penetration into a pair of β-strands can simultaneously red-shift many vibrations. The naturally short lifetime of molecular vibrations broadens these peaks beyond resolution and obscures this information in uniquely shaped ridges and bands. None of this is accounted for in a model that neglects disorder.
Although the agreement between the calculated and experimental FTIR spectra can be improved, the qualitative features are reproduced with only homogeneous broadening. Clearly, this Lorentzian approximation is incompatible with the observed 2DIR lineshapes and thus the agreement with the calculated FTIR is reached by overestimating the homogeneous broadening to compensate for neglecting inhomogeneity. These observations motivate the direction of this work; we choose to work toward a model that captures the experimental heterogeneity demonstrated in the 2DIR lineshapes rather than including more parameters to accurately fit the FTIR lineshape.
Static averaging for 2DIR
In the static averaging technique, a representative ensemble of structures is required to calculate a 2DIR spectrum that sums the individual contributions from each structure. Spectroscopically relevant fluctuations can be expected in two places: site energies (diagonal Hamiltonian elements) and couplings (off-diagonal Hamiltonian elements). The coupling fluctuations arise from flexible secondary structure that changes the orientation and distance between amide I oscillators. The site-energy fluctuations arise from the evolving hydrogen-bonding environments at each site. This nicely suggest a concerted treatment of dynamics and spectroscopy, since MD simulations simultaneously provide a set of structures as well as a description of the electrostatics.
Fig. 2 shows how the observed 2DIR spectrum arises from the average of 2DIR spectra of individual structures. In this picture, each component structure generates a distinct 2DIR spectrum with many homogeneously broadened diagonal and cross peaks. The pattern of peaks in each component spectrum is a sensitive indicator of the couplings and site energies for a particular structure. In 2DIR spectra, each homogeneous peak appears as an oppositely signed doublet. When averaged over the equilibrium ensemble, much of the off-diagonal structure disappears as a result of shifting negative and positive amplitudes. The remaining structure reflects the constructive addition of peaks along the diagonal axis, characteristic of inhomogeneous broadening, and ridges of constructively interfering cross peaks that stretch along ω1 (52). Fig. 2 shows that although the structures of the ensemble at first glance seem very similar, they vary considerably in the quantities that influence the 2DIR spectrum most: the number and geometry of hydrogen bonds.
FIGURE 2.
Two sample spectra and structures are shown for slightly different hydrogen-bonding environments calculated using the Skinner 6P site-energy model. Note that the fine structure disappears and the diagonal elongation of the 2DIR peaks arises from the static average over the equilibrium distribution of hydrogen-bonding environments characterized by N, the number of internal hydrogen bonds, and RO–N, the oxygen-nitrogen hydrogen bond distance. Twenty-one evenly spaced contours are plotted from ±50% of the maximum for each spectrum.
Fig. 3 shows the comparison of calculated 2DIR and FTIR spectra for trpzip2, D-Arg, and ubiquitin against experiment. The agreement in the experimental and calculated spectra from electrostatic site-energy models are an improvement over the degenerate model and the heuristic model presented in Fig. 1 and the Supplementary Material, which also assumes fixed (yet different) site energies. The diagonal elongation is much better represented by averaging over many structures in all of the data and using a site-energy model sensitive to fluctuating hydrogen bonds. A common deficiency in the spectra calculated from electrostatic models is the overall blue-shift relative to experiment, which can be traced to the site-energy parameterizations, many of which underestimate the red-shift that occurs upon aqueous solvation of NMA from the gas phase. All of the predicted spectra (FTIR and 2DIR) are also too broad, which may result from neglecting motional narrowing effects. It may also be an artifact of the force-field parameterization, which implicitly treats electronic polarizability by overestimating partial atomic charges to fit quantum mechanical calculations (53,54). The field-based models seem to predict even broader lineshapes for reasons discussed in the next section, which may indicate that motional narrowing effects are more important there and that a static averaging technique should use the potential-based models.
FIGURE 3.
Comparison of calculated and experimental FTIR and 2DIR for Trpzip2, D-Arg, and ubiquitin. Twenty-one evenly spaced contours are plotted from ±50% of the maximum for each spectrum.
In the trpzip2 FTIR spectra, the high frequency shoulder and correct relative peak intensity is observed in all of the calculations, which has been noted as a signature of antiparallel β-sheet structure. Many subtle features match up in the calculated and predicted 2DIR spectra. The cross-peak ridge extending horizontally to the red from the high frequency peak is observed in each of the electrostatic models, but it is weaker than the experiment in every case. The ridge extending horizontally to the blue from the most intense overtone peak is reproduced, as is the node between the fundamental and overtone peaks. Interestingly, the sharp red-side extension from the low frequency fundamental peak at ω3 ≈ 1640 cm−1 is observed in each potential model and the experiment, but not in the field models. The narrowest spectrum with degenerate site energies appears qualitatively similar to the FTIR, but the same model fails to predict the observed 2DIR lineshapes.
All of the D-Arg FTIR spectra show a singly-peaked and roughly symmetric lineshape in agreement with the experiment. The calculated 2DIR lineshapes show the broad, diagonally elongated peak, but also show a bit of extra structure unobserved in the experiment extending from the fundamental peak in the –ω1 direction. The substantial extension of the overtone in the +ω3 direction at high frequencies is underestimated in each calculation.
The ubiquitin spectra differ from trpzip2 in the intensity between the high and low frequency antiparallel β-sheet peaks arising from the α-helix and random coils. Although the calculation correctly predicts structure in this region, it is overestimated, leading to a mismatch in the relative intensity of the two main peaks. The cross-peak ridges are reproduced, as well as the sharp extension from the low frequency fundamental. The slope of the node is also predicted in good agreement. In ubiquitin like trpzip2 and D-Arg, the calculated lineshapes from electrostatic site energy models are broader than experiment.
The origin of frequency shifts in site-energy models
Each considered site-energy model was parameterized to describe the fluctuating amide I frequency of N-methylacetamide. All but Jansen 4F were parameterized with water. In extending these models to describe the amide I site energy fluctuations for various sites in a polypeptide chain, several questions arise. Should only the electrostatics of the water be included? Will the models work at all if the original definition of “solvent” is now extended to include surrounding protein? What role do the side chains and other parts of the backbone play? These questions are investigated by looking at the average site energies and which structures contribute to the red-shift from the gas phase (Table 1). In this table, the brackets 〈 〉 imply an average over site and ensemble. The average site energy is given by 〈ω〉, which tells about the typical hydrogen-bonding environment that causes a red-shift from the gas-phase value of 1717 cm−1. This cumulative shift is broken down into the average shift from water, backbone, and side chains in 〈δωWater〉 and 〈δωBackbone〉, respectively. Also note that three of the models parameterize a static red-shifting contribution (17,18,20). The average frequency standard deviation is given by 〈σ〉.
First, we observe that by summing the electrostatics from the water, side chains, and remaining backbone, the red-shift comes close to the expected region of ∼1655 cm−1. The majority of the red-shift is obtained from the water, showing that a correct parameterization of the solvent electrostatics is the most important determinant of the site energies. As noticed by Skinner, et al. (20), differences in the potential models reflect how many water molecules were used in the NMA/water cluster calculations to parameterize the model—the Keiderling 5P model used the largest clusters and the Hirst 4P and 7P models used the smallest. Not enough models are present to compare this in the field models. The field models also underestimate the contribution of the backbone by ∼10 cm−1 relative to the potential models, causing them to differ in the relative importance of backbone and side-chain contributions; the field-based models include more of a contribution from the side chains than backbone, which is opposite in the potential-based models.
The other striking difference between the field- and potential-based models are the significantly larger field site-energy standard deviations, the effects of which are also manifested as broader lineshapes in the field models. This can be rationalized by the distance sensitivity of the field 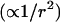 and the potential
and the potential 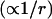 formulations and the
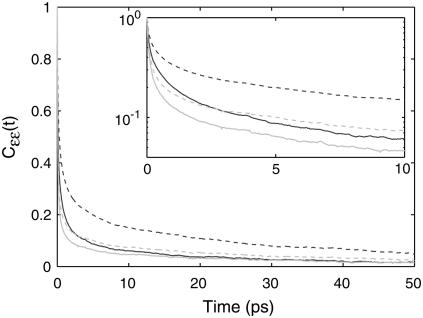
formulations and the  scaling properties of signal to noise. More atoms are significant to the potential than the field because the cutoff is slower and so the random solvent modulations will be smaller. The difference in distance scaling may also explain the inconsistency in relative backbone contributions and difference in dephasing properties. In illustration of the latter, site-energy correlation functions
scaling properties of signal to noise. More atoms are significant to the potential than the field because the cutoff is slower and so the random solvent modulations will be smaller. The difference in distance scaling may also explain the inconsistency in relative backbone contributions and difference in dephasing properties. In illustration of the latter, site-energy correlation functions  (where 〈 〉 indicate an ensemble and site average) are plotted in Fig. 4 for the total shift and water-only contribution to a representative field and potential model. A biexponential fit to reveal the general timescales shows that the short-time component is faster in the Jansen 4F model than the Keiderling 5P model (180 fs and 500 fs, respectively), indicative of the quicker randomization of frequencies induced by the larger modulations. This was also seen in the work of Jansen and Knoester (21), which was also manifested as a faster decay with fast oscillations in the frequency correlation function for NMA for the field parameterization. Similar work on NMA by Skinner et al. (20) did not reveal a difference in the standard deviations between field and potential, but did note a shorter T2* dephasing time for the field-based model than for the potential-based models.
(where 〈 〉 indicate an ensemble and site average) are plotted in Fig. 4 for the total shift and water-only contribution to a representative field and potential model. A biexponential fit to reveal the general timescales shows that the short-time component is faster in the Jansen 4F model than the Keiderling 5P model (180 fs and 500 fs, respectively), indicative of the quicker randomization of frequencies induced by the larger modulations. This was also seen in the work of Jansen and Knoester (21), which was also manifested as a faster decay with fast oscillations in the frequency correlation function for NMA for the field parameterization. Similar work on NMA by Skinner et al. (20) did not reveal a difference in the standard deviations between field and potential, but did note a shorter T2* dephasing time for the field-based model than for the potential-based models.
FIGURE 4.
The normalized site-energy fluctuation correlation function (solid line), calculated with the Keiderling 5P (dark) and Jansen 4F (light) models (a representative potential and field site-energy model, respectively) are shown, in addition to the contribution from water (dashed line) for both models.
Relative importance of coupling and site energies
With the results described above in hand it is important to ask what the delocalized eigenstates are more sensitive to: equilibrium backbone structural disorder causing changes in the coupling or hydrogen bonding and solvent disorder causing changes in the site energies. In Fig. 5, we computationally address this. We calculate the FTIR and 2DIR spectra of trpzip2 in six different ways using the Keiderling 5P potential model:
Assuming that the Hamiltonian is equal to its ensemble-averaged value.
Assuming that only the site energies are fixed equal to the ensemble-averaged values, while the couplings are sampled.
Assuming that only the coupling elements are equal to the ensemble-averaged values, while the site energies are sampled.
Allowing each element to be sampled at each step (the same as the full treatment in the previous section).
Assuming that the cross-correlation between site-energies is negligible and modeling the spectra based on Gaussian fluctuating site energies with the mean and standard deviation obtained from the MD simulation.
Comparing Assumptions 1 and 4 shows that approximating trpzip2 as one average structure, including a static distribution of different hydrogen-bonding environments at each site, is invalid, similar to the example in Fig. 1. Comparing Assumptions 2 and 3 to Assumption 4 reveals that it is the site-energy fluctuations that cause Assumption 1 to be such a poor approximation. Trpzip2 has a notably stable structure, which biases this picture to a site-energy-based one, but these results are also verified in D-Arg and ubiquitin. The spectral signatures of equilibrium variations in coupling are nearly nonexistent in these systems.
FIGURE 5.
Six exploratory calculations are presented in an attempt to identify the physical origins of spectral features in trpzip2. (A) All elements of the Hamiltonian set to their average value. (B) Site energies set to their average value, couplings sampled from MD. (C) Couplings set to their average value, site energies sampled. (D) All elements sampled. (E) Couplings set to their average value, site energies sampled from a Gaussian distribution with center and width corresponding to MD site energy statistics. Twenty-one evenly spaced contours are plotted from ±50% of the maximum for each spectrum.
This emphasizes the critical importance of fluctuating site energies in modeling 2DIR, and therefore FTIR, spectra. The results are striking in that they indicate that the site-energy fluctuations are far dominant over coupling fluctuations. By averaging out the site-energy fluctuations, the spectra appear nearly indistinguishable from the entirely static spectrum. By only surveying fluctuations in the site energies, a spectrum nearly indistinguishable from the totally averaged spectrum is obtained. The minor differences attributable to fluctuations in coupling include a slight extension of the ridge and some minor (∼1 cm−1) line broadening are more noticeable in the unconvolved stick spectra (not shown). This is both computationally fortunate and physically revealing; of the N2 elements of the Hamiltonian, the fluctuations in merely N of them determine to a large part the disorder shown in a 2DIR spectrum.
The dominance of disorder in the site energies and the relative stability of the off-diagonal elements implies that one may reduce the complexity in calculating 2DIR spectra by sampling site energies from independent random distributions, which further assumes that frequency shifts between sites are uncorrelated. In Fig. 5 E, we compare a calculation of the 2DIR spectrum obtained by modeling the spectrum based on Gaussian random fluctuations of site energies in which the mean and standard deviation of the distribution is obtained for each site from the MD simulation. The excellent agreement between Fig. 5, D and E, indicate that the independent site approximation is valid. The implication is that knowledge of a representative equilibrium structure and its fluctuations can be used to model the infrared spectroscopy. However, the sensitivity of the mean site energies to hydrogen bonding indicates that methods must be validated to assign mean site energies in the absence of explicit solvent in a trial structure.
CONCLUSIONS
We have shown that the information that is typically sufficient to model FTIR spectra does not correctly predict 2DIR spectra. This is demonstrated in the difference between experimental and predicted 2D lineshapes from one structure and arises chiefly from the sensitivity of 2DIR to different broadening mechanisms. This suggests that although the agreement between an experimental FTIR and one calculated from a single structure appears good, the interpretation may be flawed by the disparity in parameters and observables. This modeling can be refined by examining the richer, 2D lineshapes which are more sensitive to disorder.
We have pursued this by calculating FTIR and 2DIR spectra from MD simulations, while testing a set of proposed site-energies models. We obtain the best prediction of gross and subtle features in protein 2DIR spectra to date, despite the empirical force fields used to calculate electrostatics and neglecting motional narrowing effects by using static averages. Strong features such as cross-peak ridges and even many subtle lineshape features are reproduced faithfully. The most important step forward is the agreement in the diagonal elongation of peaks arising from disorder, which is typically ignored in modeling FTIR spectra. We track the origin of this disorder and find it to be based in fluctuating site energies, not fluctuating couplings. In turn, these site energies are ≈50% driven by the water solvent. The potential-based site-energy models predict that the remainder is mostly caused by the backbone, whereas the field-based site-energy models favor the side chains for most of the remaining fluctuations. These two pictures are inconsistent, but may be resolved by comparing isotopically shifted (13C and/or 18O) single sites bordering charged and hydrophobic residues.
Because 2DIR data can be acquired with the resolution to capture the fastest timescales of biomolecular rearrangement, our modeling provides the link that allows mechanistic nonequilibrium MD predictions of protein folding and aggregation pathways to be directly tested (48,55,56). The delocalized vibrational eigenstates provide mesoscopic structural variables that are more meaningful than rate constants, which may need to be rescaled based on anomalous solvent diffusion, or equilibrium constants, which are sensitive to slight errors in energy calculation in a way not necessarily indicative of an incorrect mechanism. This utility is immediately applicable to debates in the β-hairpin literature over the relative importance of forming the turn-region, hydrophobic core, and backbone hydrogen bonds, with the possibility of off-register hydrogen bonds (39,40,42,44,56,57). Furthermore, the sharp sensitivity of 2DIR to solvent electrostatics suggests a way beyond thermodynamic comparisons to test the next generation of implicit solvent models that reproduce structural transformations such as concurrent core collapse and desolvation (58–62) and anharmonic force fields (63) that preclude the need for a separate spectroscopic Hamiltonian.
The static averaging we employ for computational simplicity produces lineshapes that are broader than measured. By taking into consideration time-dependence in the adiabatic approximation, we can effectively increase the frequency resolution of the simulated spectra and sense more subtle features. A step beyond this would be to test at which point the nonadiabatic effects observed for tri-alanine (64) disappear in larger systems—to what extent will they broaden the spectra of hairpins and proteins? Further refinements in the calculation of spectroscopy are also possible, including accounting for rotation of the local transition dipoles, fluctuating values of the anharmonicity, and extension to other vibrational modes (21,65). Finally, although we have shown the effects of disorder in IR spectra, the effects of disorder on FTIR (one-quantum) and 2DIR (two-quantum) eigenstates remain to be seen and can be tested with the recently revisited bright-state analysis (30).
SUPPLEMENTARY MATERIAL
An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.
Acknowledgments
We thank Hoi Sung Chung and Adam Smith for data and help with data acquisition, Darwin Alonso and Valerie Daggett for the ubiquitin simulations, Peter Hamm for assistance with transition charge coupling, and Minhaeng Cho for the nearest-neighbor coupling map. We also thank Thomas Jansen, Kevin Jones, and Rebecca Nicodemus for helpful comments.
This work was supported by the National Science Foundation (grant No. CHE-0316736).
References
- 1.Torii, H., and M. Tasumi. 1992. Model calculations on the amide-I infrared bands of globular proteins. J. Chem. Phys. 96:3379–3387. [Google Scholar]
- 2.Hamm, P., M. Lim, and R. M. Hochstrasser. 1998. Structure of the amide I band of peptides measured by femtosecond nonlinear-infrared spectroscopy. J. Phys. Chem. B. 102:6123–6138. [Google Scholar]
- 3.DeCamp, M. F., L. DeFlores, J. M. McCracken, A. Tokmakoff, K. Kwac, and M. Cho. 2005. Amide I vibrational dynamics of N-methylacetamide in polar solvents: the role of electrostatic interactions. J. Phys. Chem. B. 109:11016–11026. [DOI] [PubMed] [Google Scholar]
- 4.Goormaghtigh, E., J.-M. Ruysschaert, and V. Raussens. 2006. Evaluation of the information content in infrared spectra for protein secondary structure determination. Biophys. J. 90:2946–2957. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Navea, S., R. Taeler, and A. de Juan. 2005. Application of the local regression method interval partial least-squares to the elucidation of protein secondary structure. Anal. Biochem. 336:231–242. [DOI] [PubMed] [Google Scholar]
- 6.Hiramatsu, H., Y. Goto, H. Naiki, and T. Kitagawa. 2004. Core structure of amyloid fibril proposed from IR-microscope linear dichroism. J. Am. Chem. Soc. 126:3008–3009. [DOI] [PubMed] [Google Scholar]
- 7.Schweitzer-Stenner, R., F. Eker, A. Perez, K. Griebenow, X. Cao, and L. A. Nafie. 2003. The structure of tri-proline in water probed by polarized Raman, Fourier transform infrared, vibrational circular dichroism, and electric ultraviolet circular dichroism spectroscopy. Biopolymers. 71:558–568. [DOI] [PubMed] [Google Scholar]
- 8.Elliot, A., and E. J. Ambrose. 1950. Structure of synthetic polypeptides. Nature. 165:921–922. [DOI] [PubMed] [Google Scholar]
- 9.Krimm, S. 1955. Frequency shift of the CO stretching band in polypeptides and proteins. J. Chem. Phys. 23:1371–1372. [Google Scholar]
- 10.Miyazawa, T. 1960. Perturbation treatment of the characteristic vibrations of polypeptide chains in various configurations. J. Chem. Phys. 32:1647–1652. [Google Scholar]
- 11.Krimm, S., and Y. Abe. 1972. Intermolecular interaction effects in the amide I vibrations of β polypeptides. Proc. Natl. Acad. Sci. USA. 69:2788–2792. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Häseler, S., A. Poglitsch, G. Bechtold, and W. L. Peticolas. 1986. Influence of water on the infrared spectrum of crystalline N-methylacetamide. J. Chem. Phys. 84:1046–1047. [Google Scholar]
- 13.Mirkin, N. G., and S. Krimm. 1991. Ab initio vibrational analysis of hydrogen-bonded trans- and cis-N-methylacetamide. J. Am. Chem. Soc. 113:9742–9747. [Google Scholar]
- 14.Mirkin, N. G., and S. Krimm. 1996. Ab initio vibrational analysis of isotopic derivatives of aqueous hydrogen-bonded trans-N-methylacetamide. J. Mol. Struct. 377:219–234. [Google Scholar]
- 15.Torii, H., T. Tatsumi, and M. Tasumi. 1998. Effects of hydration on the structure, vibrational wavenumbers, vibrational force field and resonance Raman intensities of N-methylacetamide. J. Raman Spectrosc. 29:537–546. [Google Scholar]
- 16.Torii, H., T. Tatsumi, T. Kanazawa, and M. Tasumi. 1998. Effects of intermolecular hydrogen-bonding interactions on the amide I mode of N-methylacetamide: matrix-isolation infrared studies and ab initio molecular orbital calculations. J. Phys. Chem. B. 102:309–314. [Google Scholar]
- 17.Ham, S., and M. Cho. 2003. Amide I modes in the N-methylacetamide dimer and glycine dipeptide analog: diagonal force constants. J. Chem. Phys. 118:6915–6922. [Google Scholar]
- 18.Ham, S., J.-H. Kim, H. Lee, and M. Cho. 2003. Correlation between electronic and molecular structure distortions and vibrational properties. II. Amide I modes of NMA-nD2O complexes. J. Chem. Phys. 118:3491–3498. [Google Scholar]
- 19.Bour, P., and T. A. Keiderling. 2003. Empirical modeling of the peptide amide I band IR intensity in water solution. J. Chem. Phys. 119:11253–11262. [Google Scholar]
- 20.Schmidt, J. R., S. A. Corcelli, and J. L. Skinner. 2004. Ultrafast vibrational spectroscopy of water and aqueous N-methylacetamide: comparison of different electronic structure/molecular dynamics approaches. J. Chem. Phys. 121:8887–8896. [DOI] [PubMed] [Google Scholar]
- 21.Jansen, T. l. C., and J. Knoester. 2006. A transferable electrostatic map for solvation effects on amide I vibrations and its application to linear and two-dimensional spectroscopy. J. Chem. Phys. 124:044502. [DOI] [PubMed] [Google Scholar]
- 22.Demirdöven, N., M. Khalil, O. Golonzka, and A. Tokmakoff. 2001. Correlation effects in the two-dimensional vibrational spectroscopy of coupled vibrations. J. Phys. Chem. A. 105:8025–8030. [Google Scholar]
- 23.Zhuang, W., D. Abramavicius, T. Hayashi, and S. Mukamel. 2006. Simulation protocols for coherent femtosecond vibrational spectra of peptides. J. Phys. Chem. B. 110:3362–3374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Hahn, S., S. Ham, and M. Cho. 2005. Simulation studies of amide I IR absorption and two-dimensional IR spectra of β-hairpins in liquid water. J. Phys. Chem. B. 109:11789–11801. [DOI] [PubMed] [Google Scholar]
- 25.Bour, P., and T. A. Keiderling. 2005. Vibrational spectral simulation for peptides of mixed secondary structure: method comparisons with the trpzip model hairpin. J. Phys. Chem. B. 109:23687–23697. [DOI] [PubMed] [Google Scholar]
- 26.Krimm, S., and J. Bandekar. 1986. Vibrational spectroscopy and conformation of peptides, polypeptides, and proteins. In Advances in Protein Chemistry, Vol. 38. C. B. Anfinsen, J. T. Edsall, and F. M. Richards, editors. Academic Press, New York. 181–364. [DOI] [PubMed]
- 27.Krimm, S., and W. C. Reisdorf, Jr. 1994. Understanding normal modes of proteins. Faraday Disc. 99:181–197. [DOI] [PubMed] [Google Scholar]
- 28.Torii, H., and M. Tasumi. 1998. Ab initio molecular orbital study of the amide I vibrational interactions between the peptide groups in di- and tripeptides and considerations on the conformation of the extended helix. J. Raman Spectrosc. 29:81–86. [Google Scholar]
- 29.Woutersen, S., and P. Hamm. 2002. Nonlinear two-dimensional vibrational spectroscopy of peptides. J. Phys. Condens. Matter. 14:R1035–R1062. [Google Scholar]
- 30.Chung, H. S., and A. Tokmakoff. 2006. Visualization and characterization of the infrared active amide I vibrations of proteins. J. Phys. Chem. B. 110:2888–2898. [DOI] [PubMed] [Google Scholar]
- 31.Gorbunov, R. D., D. S. Kosov, and G. Stock. 2005. Ab initio-based exciton model of amide I vibrations in peptides: definition, conformational dependence, and transferability. J. Chem. Phys. 122:22490405. [DOI] [PubMed] [Google Scholar]
- 32.Andrews, S. S., and S. G. Boxer. 2002. Vibrational Stark effects of nitriles. II. Physical origins of Stark effects from experiment and perturbation models. J. Phys. Chem. A. 106:469–477. [Google Scholar]
- 33.Suydam, I. T., and S. G. Boxer. 2003. Vibrational Stark effects calibrate the sensitivity of vibrational probes for electric fields in proteins. Biochemistry. 42:12050–12055. [DOI] [PubMed] [Google Scholar]
- 34.Eaves, J. D., A. Tokmakoff, and P. L. Geissler. 2005. Electric field fluctuations drive vibrational dephasing in water. J. Phys. Chem. A. 109:9424–9436. [DOI] [PubMed] [Google Scholar]
- 35.Hamm, P., and S. Woutersen. 2002. Coupling of the amide I modes of the glycine dipeptide. Bull. Chem. Soc. Jpn. 75:985–988. [Google Scholar]
- 36.Ham, S., S. Cha, J. Choi, and M. Cho. 2003. Amide I modes of tripeptides: Hessian matrix reconstruction and isotope effects. J. Chem. Phys. 119:1451–1461. [Google Scholar]
- 37.Frisch, M. J., G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, V. G. Zakrzewski, J. A. M. Jr, R. E. Stratmann, J. C. Burant, S. Dapprich, J. M. Millam, A. D. Daniels, K. N. Kudin, M. C. Strain, O. Farkas, J. Tomasi, V. Barone, M. Cossi, R. Cammi, B. Mennucci, C. Pomelli, C. Adamo, S. Clifford, J. Ochterski, G. A. Petersson, P. Y. Ayala, Q. Cui, K. Morokuma, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. Cioslowski, J. V. Ortiz, A. G. Baboul, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. Gomperts, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, J. L. Andres, C. Gonzalez, M. Head-Gordon, E. S. Replogle, and J. A. Pople. 1998. GAUSSIAN 98, Rev. A9. Gaussian, Pittsburgh, PA.
- 38.Smith, A. W., H. S. Chung, Z. Ganim, and A. Tokmakoff. 2005. Residual native structure in a thermally denatured β-hairpin. J. Phys. Chem. B. 109:17025–17027. [DOI] [PubMed] [Google Scholar]
- 39.Muñoz, V., P. A. Thompson, J. Hofrichter, and W. A. Eaton. 1997. Folding dynamics and mechanism of β-hairpin formation. Nature. 390:196–199. [DOI] [PubMed] [Google Scholar]
- 40.Dinner, A. R., T. Lazaridis, and M. Karplus. 1999. Understanding β-hairpin formation. Proc. Natl. Acad. Sci. USA. 96:9068–9073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Cochran, A. G., N. K. Skelton, and M. A. Starovasnik. 2001. Tryptophan zippers: stable, monomeric β-hairpins. Proc. Natl. Acad. Sci. USA. 98:5578–5583. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Wei, G., P. Derreumaux, and N. Mousseau. 2003. Sampling the complex energy landscape of a simple β-hairpin. J. Chem. Phys. 119:6403–6406. [Google Scholar]
- 43.Dyer, R. B., S. J. Maness, E. S. Peterson, S. Franzen, R. M. Fesinmeyer, and N. H. Andersen. 2004. The mechanism of β-hairpin formation. Biochemistry. 43:11560–11566. [DOI] [PubMed] [Google Scholar]
- 44.Pitera, J. W., I. Haque, and W. C. Swope. 2006. Absence of reptation in the high-temperature folding of the trpzip2 β-hairpin peptide. J. Chem. Phys. 124:141102. [DOI] [PubMed] [Google Scholar]
- 45.Huang, C. Y., J. W. Klemke, Z. Getahun, W. F. DeGrado, and F. Gai. 2001. Temperature-dependent helix-coil transition of an alanine based peptide. J. Am. Chem. Soc. 123:9235–9238. [DOI] [PubMed] [Google Scholar]
- 46.Marqusee, S., V. H. Robbins, and R. L. Baldwin. 1989. Unusually stable helix formation in short alanine-based peptides. Proc. Natl. Acad. Sci. USA. 86:5286–5290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.MacKerell, A. D., Jr., D. Bashford, M. Bellott, R. L. D. Jr, J. D. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo, S. Ha, D. Joseph-McCarthy, L. Kuchnir, K. Kuczera, F. T. K. Lau, C. Mattos, S. Michnick, T. Ngo, D. T. Nguyen, B. Prodhom, W. E. Reiher III, B. Roux, M. Schlenkrich, J. C. Smith, R. Stote, J. Straub, M. Watanabe, J. Wiórkiewicz-Kuczera, D. Yin, and M. Karplus. 1998. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J. Phys. Chem. B. 102:3586–3616. [DOI] [PubMed] [Google Scholar]
- 48.Alonso, D. O. V., and V. Daggett. 1998. Molecular dynamics simulations of hydrophobic collapse of ubiquitin. Protein Sci. 7:860–874. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Cheatum, C. M., A. Tokmakoff, and J. Knoester. 2004. Signatures of β-sheet secondary structures in linear and two-dimensional infrared spectroscopy. J. Chem. Phys. 120:8201–8215. [DOI] [PubMed] [Google Scholar]
- 50.Chung, H. S., M. Khalil, and A. Tokmakoff. 2004. Nonlinear infrared spectroscopy of protein conformational change during thermal unfolding. J. Phys. Chem. B. 108:15332–15342. [Google Scholar]
- 51.Parkin, S., B. Rupp, and H. Hope. 1996. Structure of bovine pancreatic trypsin inhibitor at 125 K definition of carboxyl-terminal residues Gly-57 and Ala-58. Acta Crystallogr. D52:18–29. [DOI] [PubMed] [Google Scholar]
- 52.Dijkstra, A. G., and J. Knoester. 2005. Collective oscillations and the linear and two-dimensional infrared spectra of inhomogeneous β-sheets. J. Phys. Chem. B. 109:9787–9798. [DOI] [PubMed] [Google Scholar]
- 53.Becker, O. M., A. D. MacKerell, Jr., B. Roux, and M. Watanabe (editors). 2001. Computational Biochemistry and Biophysics. Marcel Dekker, New York.
- 54.MacKerell, A. D., Jr. 2004. Empirical force fields for biological macromolecules: overview and issues. J. Comput. Chem. 25:1584–1604. [DOI] [PubMed] [Google Scholar]
- 55.Zhang, J., M. Qin, and W. Wang. 2006. Folding mechanism of β-hairpins studied by replica exchange molecular simulations. Proteins. 62:672–685. [DOI] [PubMed] [Google Scholar]
- 56.Bolhuis, P. G. 2005. Kinetic pathways of β-hairpin (un)folding in explicit solvent. Biophys. J. 88:50–61. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Tsai, J., and M. Levitt. 2002. Evidence of turn and salt bridge contributions to β-hairpin stability: MD simulations of C-terminal fragment from the B1 domain of protein G. Biophys. Chem. 101–102:187–201. [DOI] [PubMed] [Google Scholar]
- 58.ten Wolde, P. R., and D. Chandler. 2002. Drying-induced hydrophobic polymer collapse. Proc. Natl. Acad. Sci. USA. 99:6539–6543. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Cheung, M. S., A. E. García, and J. N. Onuchic. 2002. Protein folding mediated by solvation: water expulsion and formation of the hydrophobic core occur after the structural collapse. Proc. Natl. Acad. Sci. USA. 99:685–690. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Rhee, Y. M., E. J. Sorin, G. Jayachandran, E. Lindahl, and V. S. Pande. 2004. Simulations of the role of water in the protein-folding mechanism. Proc. Natl. Acad. Sci. USA. 101:6456–6461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Shirts, M. R., and V. S. Pande. 2005. Solvation free energies of amino acid side chain analogs for common molecular mechanics water models. J. Chem. Phys. 122:134508. [DOI] [PubMed] [Google Scholar]
- 62.Lu, H., and K. Schulten. 2000. The key event in force-induced unfolding of titin's immunoglobulin domains. Biophys. J. 79:51–65. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Gerber, R. B., G. M. Chaban, S. K. Gregurick, and B. Brauer. 2003. Vibrational spectroscopy and the development of new force fields for biological molecules. Biopolymers. 68:370–382. [DOI] [PubMed] [Google Scholar]
- 64.Jansen, T. l. C., W. Zhuang, and S. Mukamel. 2004. Stochastic Liouville equation simulation of multidimensional vibrational line shapes of trialanine. J. Chem. Phys. 121:10577–10598. [DOI] [PubMed] [Google Scholar]
- 65.Hayashi, T., W. Zhuang, and S. Mukamel. 2005. Electrostatic DFT map for the complete vibrational amide band of NMA. J. Phys. Chem. A. 109:9747–9759. [DOI] [PubMed] [Google Scholar]
- 66.Watson, T. M., and J. D. Hirst. 2005. Theoretical studies of the amide I vibrational frequencies of [Leu]-enkephalin. Mol. Phys. 103:1531–1546. [Google Scholar]