Size-Dependent Diffusion of Membrane Inclusions

Abstract

Experimentally determined diffusion constants are often used to elucidate the size and oligomeric state of membrane proteins and domains. This approach critically relies on the knowledge of the size-dependence of diffusion. We have used mesoscopic simulations to thoroughly quantify the size-dependent diffusion properties of membrane inclusions. For small radii R, we find that the lateral diffusion coefficient D is well described by the Saffman-Delbrück relation, which predicts a logarithmic decrease of D with R. However, beyond a critical radius R_c ≈ hη_m/(2η_c) (h, bilayer thickness; η_m/c, viscosity of the membrane/surrounding solvent) we observe significant deviations and the emergence of an asymptotic scaling D ∼ 1/R². The latter originates from the asymptotic hydrodynamics and the inclusion's internal degrees of freedom that become particularly relevant on short timescales. In contrast to the lateral diffusion, the size dependence of the rotational diffusion constant D_r follows the predicted hydrodynamic scaling D_r ∼ 1/R² over the entire range of sizes studied here.

INTRODUCTION

Diffusion is the basic means of transport in membranes, and the mixing of membrane components via Brownian motion is often very efficient: a lipid can rotate about its own axis within <10 μs (1) and explores ∼16μm² within a second (2). Given that speedy movement, membrane-anchored reaction partners can meet and align via diffusion and, upon doing so, create new (active) complexes or trigger signaling events downstream.

In the spirit of the above, biological membranes for a long time have been viewed as an unstructured, two-dimensional fluid into which individual proteins are embedded (“fluid mosaic model” (3)). Yet, more recently this picture was replaced by a more structured picture of cellular membranes (see Engelman (4) and Simons and Ikonen (5) for review). Several lines of evidence have been given that membrane domains (“rafts”), consisting of lipids and/or clusters of membrane proteins, compartmentalize in particular the plasma membrane. In fact, the size of raft-like inclusions in biomembranes has been reported to cover a wide range, from a few nanometers to some 100 nm (6). Bearing this in mind, the size-dependent diffusive mobility of membrane inclusions (from single proteins/lipids to raft-like domains) becomes a topical and important issue, even more so as measurements of diffusion coefficients are frequently used to determine complex formation via extracting the size of the tracked object.

For globular (i.e., spherical) objects diffusing in bulk solution, the size-dependent lateral diffusion coefficient is well described by the famous Einstein-Stokes equation D = k_BT/(cπηR) (7). Here, k_BT is the thermal energy, η the viscosity of the fluid, and R the hydrodynamic radius of the diffusing object. The numerical factor c depends on the boundary conditions at the sphere's surface and takes on the values c = 6 (c = 4) for stick (slip) boundary conditions. The calculation of the two-dimensional analog, i.e., the diffusion coefficient of an incompressible, cylindrical inclusion in a membrane (using no-slip boundary conditions), has been a challenging problem that was solved in a seminal study by Saffman and Delbrück (8):

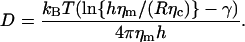(1)

Here, h is the thickness of the membrane, R is the radius of the embedded cylinder, γ ≈ 0.5772 is Euler's constant, and η_m, η_c are the viscosities of the membrane and the adjacent fluid, respectively. In essence, Eq. 1 states that D hardly varies with the radius of the inclusion, which is in strong contrast to the Einstein-Stokes equation. Unlike Eq. 1, the rotational diffusion coefficient was predicted to show a strong algebraic size dependence (8), i.e.,

(2)

The latter equation has to be compared to its three-dimensional counterpart D_r = k_BT/(8πηR³).

Several experimental studies have given support to Eq. 1 and Eq. 2 (e.g., (9,10)), whereas very recent experiments have indicated strong deviations from Eq. 1 for small and intermediate radii (11) (see also Discussion). In fact, a rigorous experimental test of the predicted size-dependences in Eq. 1 and Eq. 2 was and is very challenging due to a lack of appropriately sizable inclusions, systematic limitations in recording the diffusive movement (e.g., problems with photobleaching protocols (12)), unavoidable membrane undulations, etc., which perturb the measurement and increase the error bars of the determined diffusive mobility. This level of uncertainty in experiments underlines the importance of a comprehensive test of Eq. 1 (and Eq. 2) by alternative means. The need for a quantitative test is further highlighted by the fact that Eq. 1 spuriously predicts negative diffusion coefficients for hη_m < Rη_c. In fact, extensive hydrodynamic calculations have predicted that Eq. 1 only holds for small radii whereas for large radii a scaling D ∼ 1/R should emerge (13). It is worthwhile to note that the latter prediction as well as the derivation of Eq. 1 are based on incompressible, cylindrical membrane inclusions surrounded by incompressible fluids and the assumption of no-slip boundary conditions. All of these assumptions, although valid on the macroscopic scale, may not hold true on the meso- and nanoscale: water as well as lipid bilayers have a finite compressibility; nanoscopic membrane inclusions and larger, oligomeric (raft-like) structures can be expected to have internal degrees of freedom that reduce their lateral mobility; and finally, evidence has been given that the stick boundary condition is in general not appropriate on the molecular scale (14).

Here, we have used mesoscopic simulations of lipid bilayers with embedded, transmembrane inclusions to study the validity of Eq. 1 and Eq. 2 over a wide range of radii. We find that Eq. 1 gives a good quantitative description of the lateral diffusion coefficient up to a critical radius R_c ≈ hη_m/(2η_c). Beyond this radius, the numerically determined diffusion coefficients strongly deviate from the Saffman-Delbrück relation and a new scaling D ∼ 1/R² emerges. We give theoretical arguments that the latter arises due to the combination of the asymptotic hydrodynamic drag and internal degrees of freedom that are anticipated to become relevant for large, raft-like inclusions, especially on short timescales. The rotational diffusion coefficient on the contrary is well described by Eq. 2 over the entire range of tested radii.

METHODS

Simulation details

In the following, the position and velocity of particle i is denoted by r_i and v_i, respectively. Distances are denoted by r_ij = |r_ij| = |r_i − r_j|, whereas 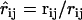is the corresponding unit vector pointing from particle j to particle i.

In all simulations, the nonbonded interaction between any two beads i, j within the interaction range r₀ was chosen to be soft-repulsive as in standard dissipative particle dynamics (DPD) models (15–17), i.e., 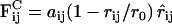, and zero for r ≥ r₀. The interaction energy a_ij (in units of the thermal energy k_BT) was tuned to achieve hydrophilic and hydrophobic beads. Bonded interactions, e.g., connections within an inclusion or lipid chain were implemented via a harmonic potential 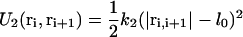. Stiffening of the chains was achieved by a bending potential U₃(r_i−1, r_i, r_i+1) = k₃[1 − cos(φ − φ₀)], where the bond angle φ is defined via the scalar product 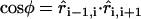. The preferred bond angle was set to φ₀ = 0.

In case of the implicit solvent model, an attractive force between any two hydrophobic beads was chosen in accordance with the approach of Cooke et al. (18): 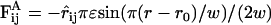for r₀ < r < r₀ + w and zero outside this range; ɛ is the attraction energy in units of k_BT and w is the typical length scale of the attraction.

Dissipative and random forces between any two beads i and j in the thermostat within the interaction range r₀ were given by 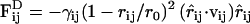and , respectively; both vanished for r ≥ r₀. Here, ζ_ij is a random variable with zero mean and unit variance that is uncorrelated for different pairs (ij) of beads and different time steps. The noise strength σ_ij is related to the dissipation strength γ_ij via the fluctuation-dissipation relation 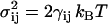(16). The cutoff length r₀ for the repulsive forces was thus the same as for all forces within the thermostat.

We have set the interaction cutoff of the thermostat r₀, the bead mass m (all beads were assumed to have the same mass), and the thermostat temperature k_BT to unity and used these parameters as basic units. We further have chosen the dissipation and noise parameters for all beads to be σ_ij = σ = 3 and γ_ij = γ = 9/2. For the explicit solvent model, we have chosen N = 4 beads per lipid chain, and the remaining interaction constants were chosen in accordance with Laradji and Kumar (19) (indices W, H, T = water, hydrophilic, hydrophobic bead): a_HH = a_WW = a_TT = a_HW = 25 k_BT, a_HT = a_WT = 200 k_BT, 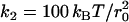, l₀ = 0.45 r₀. The interaction constants for the implicit solvent model were: a_HH = a_HT = 48 k_BT, a_TT = 96 k_BT, w = r₀, ɛ = 1.4 k_BT, 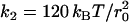, k₃ = 20 k_BT, l₀ = 0.6 r₀. For small inclusions, the linear size of the simulation box in the plane of the bilayer was chosen as L = 40 r₀; for large inclusions, L was chosen to be at least fourfold bigger than the inclusion's diameter. In all cases, the height of the simulation box was fixed to 16 r₀, which is about fourfold bigger than the membrane thickness.

We have integrated the equations of motion with a velocity Verlet scheme (20) (time increment Δt = 0.01) and imposed periodic boundary conditions. During the initial relaxation of the membrane, we used a barostat that has been adapted for the use with DPD (21) to achieve a tensionless membrane. In all simulations, we first relaxed the membrane with a single inclusion for at least 1.5·10⁴ time steps. During this time, the barostat was used to achieve a tensionless bilayer. From the final state, we iterated 10⁶ time steps during which we tracked the center-of-mass position of the inclusion and its orientation (see arrow in Fig. 1 b).

FIGURE 1.

(a) Model lipid as used in the simulations with implicit solvent (green, hydrophilic; red, hydrophobic). Hookean spring connections are indicated by cylindrical bonds. (b) Hexagonal membrane inclusion with edge length (K + 1)l₀ (K = 3). Dark/light gray corresponds to hydrophilic/hydrophobic beads; for clarity, Hookean connections are not shown. The red arrow highlights the orientation vector of the inclusion that was used to determine the rotational diffusion. (c) Snapshot of a membrane with an embedded inclusion (K = 7) after simulation of ∼80 μs real time.

Conversion to SI units

For the implicit solvent approach, we related our data to SI units by choosing the length scale as 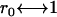nm, which yielded a bilayer thickness h ≈ 3.3 nm similar to synthetic membranes (22). This value was obtained by averaging the distance of all hydrophilic lipid head beads in the opposing leaflets of the bilayer (“phosphate-to-phosphate distance”). The internal timescale was determined by comparing the numerically obtained diffusion coefficient of a single lipid with experimentally measured values (2) 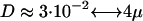m²/s (see also (23)). A single time step (Δt = 0.01) corresponded to a real time of ∼80 ps, i.e., the total time simulated was in all cases 80 μs, whereas the typical membrane patch was ∼80 nm × 80 nm. In the explicit solvent case, r₀ and Δt = 0.01 corresponded to 1.1 nm and 97 ps, respectively. Using the mentioned conversion to SI units, we determined here also the viscosity η_c of the pure solvent by monitoring the diffusion coefficient of differently sized cylinders with hexagonal cross section (diameter 2 k + 1 beads; length 2 k beads; bead-bead distance l₀ = 0.45 r₀) in a “water box” with particle density 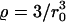. For a single solvent bead, a radius was assumed and the hydrodynamic radii of the diffusing cylinders were set to R_h = kl₀ + R₀/2, which was ∼15% larger than the radius of gyration. From the Einstein-Stokes equation (modified with the contribution by internal modes, see Results and Discussion), we determined the viscosity of the solvent to be η_c ≈ 0.03 Pa s. Bearing in mind the somewhat vaguely defined radii R_h (due to the use of soft-core potentials) and the uncertainty if stick or slip boundary conditions are more appropriate, the value for η_c may be slightly higher or lower.

Data evaluation

We briefly derive Eq. 3. Starting with a particle at r = 0 at time t = 0, one obtains from the two-dimensional diffusion equation the probability of finding the particle in an infinitesimal area element dA = 2 πrdr around the locus r at time τ as p(r)dA = 2 exp(−|r|²/(4Dτ))/(4Dτ)rdr. Changing variables to the quadratic distance ξ = r², one obtains the differential distribution of squared increments as p(ξ) = exp(−ξ/(4Dτ))/(4Dτ)dξ. For the purpose of fitting, the integrated distribution (Eq. 3) is more convenient as it does not suffer from the choice of the bin size. This approach has also been applied successfully in single-particle tracking studies (24).

RESULTS AND DISCUSSION

To study the diffusion of large inclusions in a self-assembling lipid bilayer, we have used efficient mesoscopic simulations. We used two related coarse-grained molecular dynamics simulation methods that belong to the class of DPD schemes (15–17) (see Methods for simulation details): an explicit solvent model (“standard DPD”) and an implicit solvent approach. The latter has recently been studied in some detail (18,25,26) and yields a very efficient way to simulate large membranes that are virtually untractable by standard DPD. In the remainder, we will thus concentrate on the implicit-solvent model as this approach allowed us to investigate much larger inclusions than with an explicit solvent approach. We will however compare the results to those obtained with the explicit solvent whenever possible.

In the simulations, individual lipids were considered as chains of N = 3 beads connected by Hookean springs with each bead representing a number of atoms (e.g., several methyl groups). The first bead represented the hydrophilic headgroup, the N − 1 consecutive beads represented the hydrophobic tail (cf. Fig. 1 a). The chain was given a bending rigidity, i.e., a straight chain was energetically preferred. Inclusions were modeled by cylinders with a length of 2 N beads and a hexagonal cross section (cf. Fig. 1 b). The first and last bead in each chain were taken to be hydrophilic, the remaining N − 2 were taken to be hydrophobic. In correspondence with the lipids, the beads in each chain were connected by Hookean springs and the chain was given a bending rigidity. These 2 N bead chains were positioned on all inner vertices of a plane hexagon with edge length K + 1 and were connected layerwise by Hookean springs. In total, the inclusion consisted of 2 N{3 K(K + 1) + 1} beads.

All beads interacted via a pairwise soft-repulsive potential, where the strength of repulsion was tuned to be stronger between hydrophobic-hydrophilic pairs. All beads were further subject to a Galilean-invariant, momentum-conserving DPD thermostat that included dissipative and random forces (see Methods). The solvent-induced attraction of the lipids was mimicked by an attractive pairwise potential among the hydrophobic beads in agreement with Cooke et al. (18). For comparison with Eq. 1 and Eq. 2, we have transferred the simulation units to SI units (see Methods).

We first confirmed that the chosen lipid model allowed for a self-assembling bilayer with the correct membrane fluctuations (data not shown) and an approximate thickness of h ≈ 3.3 nm (see Methods). We also inspected the integrity of the membrane during and after the simulation with and without inclusions. In all cases, the membrane was intact over the entire simulation period; a representative snapshot at the end of a simulation with a medium-sized inclusion is shown in Fig. 1 c. To quantify the lateral diffusion coefficients D, we recorded the position of the inclusion and calculated from this the integrated distribution of squared distances Δx² traveled in a period τ within the plane of the membrane, which should coincide with (see Methods)

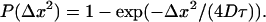(3)

A similar approach was used to obtain D_r by virtue of tracking the orientation of the inclusion (see arrow in Fig. 1 b).

In Fig. 2, the numerically obtained data for two representative inclusions (K = 2, 19) are shown together with the best fit according to Eq. 3. A clear shift to smaller quadratic distances Δx² is visible for the larger inclusion, highlighting the reduced diffusive mobility. We next determined systematically the lateral diffusion coefficient D for inclusions of various sizes. For comparison with Eq. 1, we assigned each hexagon a radius R = l₀(K + 1) = (K + 1)·0.6 nm (cf. Methods). The dependence of D on R is shown in Fig. 3 together with the best fit according to Eq. 1, from which we obtain the viscosity η_m ≈ 0.25 Pa s of the bilayer (via h ≈ 3.3 nm, Methods). This value is in good agreement with typical data from the literature (22). For the simulations with explicit solvent, we also find a very good agreement with Eq. 1 for small radii (Fig. 3, inset) and the determined parameters (h ≈ 3.5 nm, η_m ≈ 0.19 Pa s) agree well with those obtained for the implicit solvent approach. From the fit, we further obtain via hη_m/η_c ≈ 14.7 nm the effective viscosity η_c ≈ 0.056 Pa s of the surrounding (explicit solvent: η_c ≈ 0.039 Pa s). Both values for η_c correspond well to the independently determined viscosity of the solvent (see Methods) albeit η_c is not a well-defined quantity in the implicit-solvent approach (see Discussion).

FIGURE 2.

Integrated distribution P(Δx²) of squared distances Δx² traveled within a period τ = 0.8 μs for inclusions with K = 2 and K = 19 (solid and shaded lines, respectively). Best fits according to Eq. 3 are shown as symbols.

FIGURE 3.

Lateral diffusion coefficient D as a function of the inclusion radius R (symbols) is well described by the Saffman-Delbrück relation Eq. 1 (solid line) for small radii. Beyond a critical radius R_c ≈ hη_m/(2η_c) (dash-dotted line), deviations become visible and the data are best described by Eq. 4 (dashed line). (Inset) The diffusion coefficient as obtained from the explicit-solvent model (•) is well described by Eq. 1 (solid line) for small radii.

Although for small radii the Saffman-Delbrück relation yields a very good description, strong deviations are visible beyond a critical radius R_c ≈ hη_m/(2η_c) ≈ 7.4 nm. (Fitting the entire numerical data with Eq. 1 alone results in a very bad description (data not shown.)) We would like to note that the critical radius R_c emerges naturally here when comparing the flux of energy dissipated by the bilayer and the solvent, respectively: whereas the former is J_m ∝ 2 πRhη_m, the latter is given by J_c ∝ 2 πR²η_c, i.e., a crossover is expected at R = 2 R_c beyond which the friction due to the solvent-facing area dominates. For 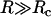, the problem can thus be reduced to the edgewise motion of a thin disk in a fluid of viscosity η_c for which one finds (with appropriate prefactors) D = k_BT/(16 Rη_c) (13).

However, inspecting our numerical data, the lateral diffusion coefficient seems to decrease faster than linear with the radius of the inclusion. How can we rationalize this observation? We recall that all hydrodynamic calculations have used incompressible cylinders as a model for the membrane inclusion (8,13); in better words, internal degrees of freedom that are likely to play a role in particular for larger inclusions/rafts have been neglected, although they are naturally included in our simulations due to the construction of the inclusion. As the inclusion's Brownian motion is driven by the erratic impact of surrounding lipids, we have to take into account that this impact will be dissipated in part by internal degrees of freedom of the inclusion via the imposed thermostat, i.e., only a fraction ϕ of the impact will be used to move the center of mass. This fraction may be estimated as follows. By construction, all beads within the inclusion perform Brownian motion in a harmonic potential of stiffness k₂ (see Methods). The spectral density for each bead is thus given by 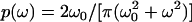with ω₀ = k₂/β, where β is the (local) friction coefficient of the moving bead, which depends on the dissipation strength of the thermostat. Coupling of the individual beads now leads to a spectrum of relaxation times, the maximum of which can be estimated by considering an effective Maxwell element (spring-dashpot in series) along the diameter of the inclusion. This Maxwell element consists of 2 K + 1 springs of stiffness k₂ and a damping dashpot of viscosity η_M in series, i.e., in total a spring with stiffness k₂/(2 K + 1) needs to be considered, yielding a relaxation time τ = (2 K + 1)η_M/k₂. Only frequencies ω < 2 π/τ are not dissipated within the inclusion (and thus can move the center of mass), that is, 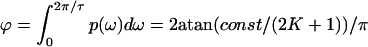. Using R ∼ 2 K + 1, it becomes clear that due to the internal dissipation only a fraction ϕ = 2atan(c/R)/π is available for the center-of-mass motion. We thus arrive at a scaling

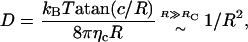(4)

which for c ≈ 6 nm describes the numerical data very well when using the previously found viscosity η_c ≈ 0.056 Pa s (Fig. 3). We would like to emphasize that c ∼ k₂/η_M, i.e., for an incompressible inclusion (k₂ → ∞, η_M → 0), the hydrodynamic scaling D ∼ 1/R (13) is obtained. We also would like to note that the critical radius R_c (which is a hydrodynamic quantity) does not have to be involved to derive Eq. 4, as the presented thermodynamic considerations do not rely on the dimensionality or the existence of an interface. Although Eq. 4 should naturally hold when quantifying the diffusive motion on short and intermediate timescales, the contribution of the internal modes can be expected to subside when monitoring the diffusive mobility over asymptotically large times (similar to a random-coil polymer that behaves asymptotically like a diffusing sphere). In this asymptotic regime, one can expect to obtain the hydrodynamic result according to Hughes et al. (13) even when internal modes are present.

We finally monitored the size dependence of the rotational diffusion coefficient D_r. For all tested inclusion sizes, the decrease of D_r is well described by Eq. 2 (Fig. 4). The prefactor of the best fit to the data yields k_BT/(4 πη_mh) ≈ 0.45 μm²/s, which is in excellent agreement with the value 0.41 μm²/s obtained from h and η_m as determined by fitting the lateral diffusion coefficient for small radii. Similarly, we found good agreement with Eq. 2 for the data obtained with the explicit-solvent model (Fig. 4, inset).

FIGURE 4.

Rotational diffusion coefficient D_rot is well described by Eq. 2 (solid line) in the implicit-solvent case and in the explicit-solvent model (inset).

DISCUSSION

In conclusion, we have shown by means of extensive simulations that the rotational diffusion coefficient of membrane inclusions follows indeed the predicted form, Eq. 2. The lateral diffusion coefficient, however, does only follow the Saffman-Delbrück relation, Eq. 1, for small radii, whereas for large radii we find substantial deviations and an asymptotic scaling according to Eq. 4. The latter takes into account the internal degrees of freedom of the inclusion, which should arise naturally as larger inclusions are most likely loosely associated protein oligomers and/or raft-like entities. The proposed scaling Eq. 4 is thus expected to be more realistic than the results derived for large incompressible cylinders. Although the internal modes can be expected to subside when following the diffusion trajectory over asymptotically long times, they clearly contribute significantly to the diffusion on small and intermediate timescales and may thus be accessible experimentally, e.g., by fluorescence correlation spectroscopy. Small deviations from Eq. 1 are also expected (and observed, cf. Fig. 3) for radii R < 1 nm, since in this regime the discrete composition of the membrane from individual lipids must be taken into account (“free-volume model” (27,28)).

It is worthwhile to note that we found similar results by two simulation approaches (i.e., using an implicit and an explicit solvent) that also differed in the type of lipids (implicit solvent N = 3 beads per lipid, explicit solvent N = 4). We furthermore have used the approach of Shillcock and Lipowsky (29) (i.e., a lipid with N = 7) and did find similar results for the diffusion coefficient (D ≤ 1μm²/s, η_m ≈ 0.2 Pa s). We are therefore confident that the lipid model influences the presented results only weakly, e.g., by slightly altering the value of η_m.

At first glance it is surprising that the implicit-solvent approach, where η_c = 0 by definition, can reproduce hydrodynamic relations like Eq. 1 in which a finite value for η_c is needed. The reason for this can be traced back again to the internal modes of the inclusion and the dissipative forces imposed by the thermostat. The erratic impact of the surrounding lipids excites shear modes within the inclusion with a polarization perpendicular to the bilayer normal, and these modes are dissipated by the action of the thermostat. A “neutral layer” of the inclusion located roughly in the midplane of the bilayer therefore feels a friction with respect to the layers that lie above and below in-plane with the hydrophilic headgroups of the lipids. Hence, these shear modes mimic an apparent solvent viscosity that should change, when the dissipation strength γ in the thermostat is altered for the beads within the inclusion. Indeed, we have observed that a reduction of γ within the inclusions leads to an effective reduction of η_c (data not shown). Efforts to thoroughly quantify the nontrivial connection between the emergence of an apparent solvent viscosity and the inner modes beyond this qualitative argument as well as an investigation that hydrodynamic quantities can be faithfully reproduced by an implicit-solvent scheme are currently under way.

In a recent report, strong deviations from Eq. 1 that indicate a scaling D ∼ 1/R have been found experimentally (11). In fact, the authors claim deviations already for radii R ≈ 1 nm, which is in contrast to earlier studies (9,10). We would like to point out here that substantial deviations from Eq. 1 should be possible only for R ≤ 1 nm (due to the free-volume model, which also predicts D ∼ 1/R for sufficiently small R (28)) or for R > R_c ≈ 10 nm. Bearing in mind the unavoidable systematic limitations when experimentally assessing the diffusive mobility and given that D ∼ 1/R can provide a reasonable fit to Eq. 1 when error bars are big enough, it is likely that the signatures of Eq. 1 have been masked in the data presented in Gambin et al. (11). Nevertheless, it will be interesting to revisit the approach of Gambin et al., i.e., i), to also use a complementary experimental techniques (e.g., fluorescence correlation spectroscopy) and ii), to extend the study to larger radii and higher temporal resolution where Eq. 4 can be expected to become visible.