Structured Water Layers Adjacent to Biological Membranes

Abstract

Water amid the restricted space of crowded biological macromolecules and at membrane interfaces is essential for cell function, though the structure and function of this “biological water” itself remains poorly defined. The force required to remove strongly bound water is referred to as the hydration force and due to its widespread importance, it has been studied in numerous systems. Here, by using a highly sensitive dynamic atomic force microscope technique in conjunction with a carbon nanotube probe, we reveal a hydration force with an oscillatory profile that reflects the removal of up to five structured water layers from between the probe and biological membrane surface. Further, we find that the hydration force can be modified by changing the membrane fluidity. For 1,2-dipalmitoyl-sn-glycero-3-phosphocholine gel (L_β) phase bilayers, each oscillation in the force profile indicates the force required to displace a single layer of water molecules from between the probe and bilayer. In contrast, 1,2-dipalmitoyl-sn-glycero-3-phosphocholine fluid (L_α) phase bilayers at 60°C and 1,2-dioleoyl-sn-glycero-3-phosphocholine fluid (L_α) phase bilayers at 24°C seriously disrupt the molecular ordering of the water and result predominantly in a monotonic force profile.

INTRODUCTION

Cell membranes mediate numerous biological processes at the cellular level with the initial interaction of many processes such as membrane insertion, transport, and fusion occurring at the lipid/water interface (1). The diffusion of molecules into a cell is governed by the lipid solubility of the permeating molecule, with small hydrophobic molecules generally crossing the membrane more easily than water-soluble molecules or ions (Overton's rule) (2). Recent studies now suggest that the sieving properties of membranes are not just a matter of simple diffusion, but also rely on complex mechanisms involving membrane proteins and transport carriers, or chaperones (3). However, an alternative view, but not mutually exclusive, is that permeability is also determined by the path that the molecules take to get to the membrane. For instance, the presence of structured or bound water layers may pose a serious obstacle to the transport of permeant molecules. Thus, it is important to consider that the displacement of water molecules before a protein directly interacts with the membrane may contribute to a rate-limiting step in permeation.

It is known that water molecules adjacent to a lipid bilayer experience a heterogeneous surface relative to their molecular size and interact strongly with lipid headgroups. This strong interaction disrupts the hydrogen bonding within the water and may extend several molecular diameters from the surface (4). For the 1,2-dipalmitoyl-sn-glycero-3-phosphocholine (DPPC) phospholipids studied here, the use of algorithms shows the presence of four distinct regions of water based on the local density as a function of the distance from the membrane surface (5). Two regions of the water correspond to a first and second solvation shell surrounding the phosphocholine groups. The extent of lipid hydration is also revealed in simulated and experimental gel (L_β) and fluid (L_α) phase DPPC membranes that can imbibe up to ≈11 and >20 water molecules per lipid (6–8), respectively, in addition to large clathrate-like structures solvating the positively charged N(CH₃) choline headgroups (9). Water at such a hydration level may remain unfrozen at temperatures below 0°C (10). Also, it is suggested that this interfacial water has lower diffusion coefficients than the bulk water (11). Thus, the unique properties of this water may play a critical role in functions such as membrane permeation.

The force required to remove strongly bound water molecules from between approaching biological surfaces, or indeed any type of surface, is termed the hydration force (12). In particular, if adequate pressure between two approaching nonbiological surfaces is reached, a single water layer can be displaced laterally into the bulk, leaving the remaining molecules free to disorder in the newly unoccupied space. Repeating ordered and disordered states of the water molecules as the two surfaces approach gives rise to an oscillatory hydration force acting between them, where the periodicity of the oscillations relates to the size of the water molecule (13,14). Ever since the first oscillatory force measurements were made with the surface force apparatus (SFA) (13), atomic force microscopy (AFM) has increasingly been used to measure oscillatory forces between a nanometre-sized probe and various substrates in pure water. Cleveland et al. (15) measured the thermal noise of the cantilever to determine interaction potentials close to hydrophilic cleavage planes of ionic crystals calcite (CaCO₃) and barite (BaSO₄). They found that the potential oscillated with a periodicity of 0.1–0.3 nm, indicating the layering of water at the tip or sample. Subsequent dynamic techniques such as small-amplitude and transverse force AFM have instead directly measured the stiffness and damping oscillations of water confined between a small probe and mica substrate (16,17). Jarvis et al. (14,18) developed the use of frequency-modulation AFM (FM-AFM) with a carbon nanotube (CNT) probe to observe oscillatory forces in the vicinity of self-assembled monolayers (SAM) of (COOH(CH)₂)10-SH on atomically flat Au-111 in liquid. In particular, this technique had the unique advantage of performing high-resolution imaging before measuring the oscillatory force and allowed for nanoscale positioning of the probe over regions of interest on the surface. Recently, Uchihashi et al. (19) performed similar measurements above SAM substrates and directly quantified the oscillatory forces from the measured frequency shifts. For a recent review on the molecular structure of water at interfaces, including the study of confined water using AFM and SFA, see Verdaguer et al. (20).

With respect to lipid membranes, osmotic pressure (OP) and SFA have been used to measure the force over large areas (e.g., 100 μm) between two lipid bilayers at small separation distances of a few nanometers. These measurements revealed a monotonic, repulsive force (not oscillatory), which initiated ongoing studies to investigate whether these repulsive forces were due to hydration or steric repulsion of the lipid headgroups (21,22). Due to the presence of only a monotonic force profile it is believed that lipid surfaces, and biological surfaces in general, do not promote the detection of oscillatory hydration forces because of their thermally mobile surface groups and increased surface roughness, both of which may smear out the oscillatory force leaving only a monotonic component. In contrast here, we investigate the nature of short-range forces for a nanometer-sized probe (CNT tip) approaching supported lipid bilayers (SLBs) by applying our modified AFM technique to the gel and fluid phases of DPPC membranes and the fluid phase of DOPC membranes in pure water. In recent years, SLBs on solid substrates have provided a good model for the fundamental study of biomembrane processes, as they are able to conserve their natural fluidity and overall biomimetic properties. For these AFM measurements, the confinement area is comparable to the cross-sectional area of a single biological molecule, such as a protein, thus mimicking the hydration forces that the molecule would experience in the same environment.

MATERIALS AND METHODS

Attachment of carbon nanotubes to AFM cantilever tips

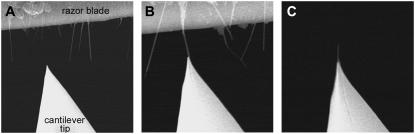
A multiwall CNT was attached to the cantilever tip using a specially designed Hitachi-S4300 field emission scanning electron (FESEM) that had an inbuilt fine piezo controlled manipulator. Firstly, a razor blade edge with aligned carbon nanotubes, prepared using an electrophoresis technique (23), and the cantilever were placed on separate sample stages in the FESEM (Fig. 1 A). Using the manipulator, a single CNT was brought up against the side of the cantilever tip at an appropriate angle and subsequently attached by focusing the electron beam on the region of overlap (Fig. 1 B). This effectively welded the CNT onto the tip by depositing amorphous carbon from the beam. The CNT was then cut to a length <500 nm by applying a pulse voltage across the razor blade and tip, allowing for the production of CNT tips with control over both the direction and length of the nanotube (Fig. 1 C).

FIGURE 1.

(A) FESEM image showing a cantilever tip and razor blade edge with aligned mutliwall carbon nanotubes, each positioned on a fine piezo controlled stage inside the FESEM. (B) A nanotube is positioned against the tip and attached using carbon deposition from the electron beam. (C) A carbon nanotube tip prepared from the sequence in panels A and B showing the ability to control both the direction and length of the tube.

Preparation of cantilevers for magnetic activation

Firstly, EFM nanosensor cantilevers were calibrated and had measured spring constants ranging from 1.5 to 2.2 N/m. A glass encapsulated neodymium/boron/iron (NdBFe) particle was then glued (Epotek 41) onto the back of each cantilever, directly behind the tip, with the aid of a light microscope and micromanipulator. The particles were magnetized using an impulse magnetizer (ASC Scientific, Carlsbad, CA (model IM-IO-ZO)) by positioning the cantilevers at an angle of 12° from the normal surface (i.e., tip angle in AFM holder) and applying a charging voltage of 300 volts, corresponding to a magnetic field strength of 37.3 kGauss, for 30 s.

Operation of FM-AFM

We used a modified Asylum Research MFP 3-D AFM (stand alone) (Santa Barbara, CA) to perform FM-AFM imaging and force spectroscopy in liquid (24). This was achieved by implementing magnetically activated dynamic mode (MAD mode), whereby the functionalized cantilever with attached magnetic particle was oscillated by applying an external magnetic field via a solenoid positioned underneath the sample stage. For this setup, the voltage to the coil was amplified using a homemade “coil driver” and the solenoid replaced the position of the objective lens in the AFM base. To regulate the FM-AFM detection scheme, we used a Nanosurf (Liestal, Switzerland) phase-loop-lock controller/detector (PLL). The PLL used two feedback systems to control the dynamic force measurements. One feedback system kept the oscillation amplitude of the cantilever constant by varying the driving voltage to the coil. A second feedback system shifted the phase signal of the lever response to 90°, which was then used as the excitation signal, to keep the lever oscillating at its fundamental resonance frequency. By monitoring changes in the resonance frequency and excitation amplitude required to keep constant oscillation amplitude, we were able to measure frequency shift and dissipation caused by the tip sample-interaction. The AFM was controlled using a modified version of the Asylum Research software (IGOR Pro, Wavemetrics).

Conversion of frequency shift to force

To convert the observed frequency shift into an interaction force 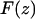the recently proposed arbitrary amplitude formula (25) was used,

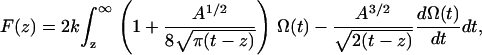(1)

where k is the spring constant, A is the oscillation amplitude of the tip, 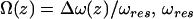is the natural resonance frequency of the cantilever in the absence of an interaction force, and z is the distance of closest approach between the tip and the surface. 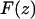is the conservative component of the interaction force between tip and sample, and does not include any contribution due to dissipative effects. As we integrate the frequency from z to infinity, the z term could be given an arbitrary zero value or reference point (i.e., the z-data is typically offset to zero). Thus, we describe the z-values as being a separation distance or simply a displacement. Using an arbitrary zero had no effect on the force conversion, as described in (25) The derivative step results in an accentuation of mostly the frequency noise, as opposed to the oscillations. Accentuation of the oscillations is minimized, as the differentiated numerical values are further integrated. The formula is valid for any amplitude and requires that the interaction force is continuous throughout the measurement. The constant-amplitude FM-AFM approach implicitly decouples the influence of conservative and dissipative force, thus Eq. 1 provides a direct connection between the change in frequency and the true interaction force, and is a dynamic analogy of Hooke's law (used for static mode AFM). The arbitrary amplitude formula unifies two previous well-established formulas that describe the relationship between the frequency shift and force (26,27). In addition, the formula has also been experimentally validated by quantifying the oscillatory forces of octamethylcyclotetrasiloxane (OMCTS) liquid whereby the forces scaled appropriately with A and, importantly, agreed with the forces previously measured for the same liquid using a different technique (i.e., surface force apparatus) (28). Errors of <5% directly associated with the formula have already been determined (25).

Technique for preparing SLBs

We prepared SLBs of DPPC and DOPC using the “solution spreading” method (i.e., swelling of cast films), which involved hydrating already adsorbed dried lipid films on mica that swell to form bilayers. This simple technique has been shown to be successful for preparing stable lipid bilayers that are suitable for studying time-dependent and physiological biomembrane processes (29). For example, DMPC ripple phases (30), mixed DPPC/DOPC (29) phases, and the processes of cationic DODAB bilayer formation on mica (31) have all been investigated using the “solution spreading” technique. In addition, the technique results in the formation of defects in the bilayer (i.e., nonuniform coverage), which provided the advantage of using exposed regions of the mica/substrate as a point of reference for measuring correct bilayer heights. In our case, complete bilayer coverage was not essential because the AFM can pinpoint regions of interest on a nanometer scale and thus avoids defects and vacancies/holes in the lipid surface.

Solution spreading method for preparation of lipid bilayers

We followed a modified method of Maeda et al. (30) to prepare lipid bilayers using the “solution spreading” technique. For this method, DPPC and DOPC were purchased in powder form (Sigma, St. Louis, MO; >99% TLC) and were used without further purification. DPPC and DOPC were separately dissolved in a filtered 1:1 chloroform (Fluka, Milwaukee, WI)/ethanol (Merck, Rahway, NJ) solution to a concentration of 1 mg/ml. The lipid solutions were vortexed and sonicated for 10 min (3 cycles) and then diluted to concentrations of 50 μg/ml, 100 μg/ml, 250 μg/ml, and 500 μg/ml solutions using the chloroform/ethanol mixture. In a laminar flow cabinet, 3 μL of the diluted DPPC and DOPC solutions (the different concentrations were tested) were dropped onto freshly cleaved mica surface to form pure bilayers of each type of lipid. The solvent was allowed to evaporate and left for 15–20 h in a laminar flow or dessicator for further drying. 250 μl of pure water was then added to the mica, washed three times by exchanging the solution, and then put onto the AFM sample stage for imaging.

Surface coverage of DPPC gel phase lipid bilayers

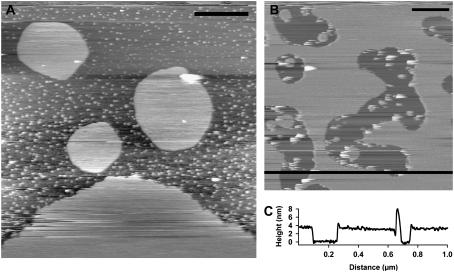
By varying the concentration of the lipid/chloroform solution deposited onto the mica, we were able to control the deposition of the bilayers. At low concentrations of 50 μg/ml DPPC/chloroform solution, AFM height images at 24°C revealed large areas of mica with sparse coverings of lipid islands (arrows) that were typically 1–5 μm in size (Fig. 2 A). No defects in the underlying layer were observed at this low concentration. As the “solution spreading” technique does not form uniform bilayers with no defects, the smooth underlying layer was therefore confirmed to be mica. Fig. 2 B shows a higher resolution image of a typical island formed at low concentrations of 50 μg/ml. At higher concentrations of 100 μg/ml, we observed lipid islands that were greater in size and contained their own defects (arrows), though smaller islands still existed on the surface (Fig. 2 C). Again, no defects were observed in the underlying surface of Fig. 2 C, confirming the presence of mica. Increasing the concentration to 250 μg/ml revealed the formation of near full-coverage lipid bilayers on the mica (Fig. 2 D), though defects in the lipid bilayer were consistently observed. No defects were observed in the underlying substrate, though this was sometimes difficult to distinguish in samples where the bilayer had few defects of small size. At the highest concentration of 500 μg/ml, multiple stacks of bilayers were observed and easily recognized by continual height changes across the surface (Fig. 2 E). The lightest areas corresponded to the top-most layer, whereas underlying layers were distinguished by darker areas that still contained defects. We were able to determine that up to two to three bilayers were typically present at this concentration. Using the mica substrate as a reference, a cross-sectional height analysis of the lipid membranes revealed a mean height of 4.9 ± 0.1 nm (mean ± SE; n = 56) (data not shown), which agreed with previous AFM height values recorded for DPPC (32) and indicated the formation of single lipid bilayers. The bilayer height is highlighted in Fig. 2 F that shows a histogram of the height for the entire bilayer area in Fig. 2 C. The histogram was obtained using a mask that selected all regions of the bilayer and then by calculating the height at each pixel within the mask. All images in Fig. 2 were representative of the corresponding lipid concentration and therefore lipid concentrations of 100 μg/ml and 250 μg/ml were used to ensure that only single bilayers directly on mica were used for the force measurements.

FIGURE 2.

(A) DPPC lipid sample prepared using 50 μg/ml concentration showing several small lipid islands (arrows) directly on the mica surface. Scale bar, 10 μm (B) Higher resolution image of a typical lipid island observed in panel A. Scale bar, 1 μm. (C) Lipid sample prepared using 100 μg/ml concentration showing the formation of a lipid island of greater area with small defects (arrows). Scale bar, 1 μm. (D) Lipid sample prepared using 250 μg/ml concentration showing near full coverage of the lipid bilayer. Scale bar, 1 μm. (E) Lipid sample prepared using 500 μg/ml concentration showing the formation of multilayered bilayers. Scale bar, 1 μm. (F) Histogram of the bilayer height calculated from the entire lipid area in panel C showing a bilayer height of 4.86 nm.

DPPC gel and fluid phase separated domains in SLBs

In contrast, DPPC lipid membranes at 50°C revealed two domain regions within the bilayers that corresponded to regions of a higher gel phase (lighter areas) and lower fluid phase (darker areas) (Fig. 3 A). The difference in height between the two DPPC phases, namely the bilayer thickness (D_B) and acyl chain length (D_C), has previously been confirmed using liquid crystallography and diffraction measurements (33). For the gel phase, the values for D_B and D_C were 47.8 Å and 34.4 Å, respectively, whereas for the fluid phase respective values of 38.5 Å and 28.5 Å indicated that the bilayer is thinner (33). The transition at 50°C from the gel to fluid phase has also been previously demonstrated for SLBs using AFM (32,34). These studies described that in the fluid phase the melted chains were disordered and condensed resulting in domains with lower height, whereas coexisting gel phase domains were higher due their well-ordered and extended chains that had yet to melt (34). Fig. 3 B shows an image of the same region in Fig. 3 A after the bilayer has been heated well past the transition temperature to 60°C. In this case, the membrane underwent complete transition to the fluid phase and the domains were no longer observed. A histogram of the height difference (Fig. 3 C) between the two phases in Fig. 3 A revealed a value of 0.98 nm, which agreed with previous values (32) and confirmed the presence of the phase separation. It is also noted that on occasions ripple phases were observed around the transition temperature (data not shown).

FIGURE 3.

(A) DPPC lipid sample imaged at 50°C showing lipid bilayer with gel and fluid phase separated domains. Lighter areas correspond to higher regions of gel phase, whereas darker areas correspond to lower regions of fluid phase. Scale bar, 0.2 μm. (B) Image of the same region in panel A obtained at 60°C. No phase-separated domains are observed due to the complete transition of the bilayer to the fluid phase. Scale bar, 0.2 μm (C) Histogram of height difference between the gel and fluid phase regions in panel A using the masking method described above in Fig. 2 F.

DOPC fluid phase bilayers

To obtain a reasonable surface coverage of DOPC and ensure that only single bilayers were formed on the mica, we used similar lipid concentrations of between 100 μg/ml and 250 μg/ml. Fig. 4 A shows large islands of DOPC bilayers formed at a concentration of 100 μg/ml, whereas higher concentrations of ≈250 μg/ml produced a bilayer with greater surface coverage and defects (Fig. 4 B). In these DOPC samples, small lipid vesicles were observed only adhering to the mica. A cross section of the bilayer taken across the black line in Fig. 4 B indicated a height of ≈ 3.8 nm, which is consistent with the height of DOPC measured in previous studies (35).

FIGURE 4.

(A) DOPC lipid sample prepared using 100 μg/ml concentration showing large lipid islands directly on the mica surface, in addition to numerous small vesicles. Scale bar, 0.5 μm. (B) Lipid sample prepared using 250 μg/ml concentration showing greater surface coverage and defects. Scale bar, 0.2 μm. (C) Height cross-section taken across black line in panel B indicating a bilayer height of ≈3.8 nm.

FM-AFM force measurements on gel and fluid phase bilayers

DPPC and DOPC lipid samples on mica were placed on the normal AFM sample stage or Bioheater (Asylum Research) fluid cell to conduct measurements at different temperatures. For the bioheater, a closed loop feedback was used to maintain the sample temperature to within 0.1°C and lipid bilayers were heated up with a 6°C/min ramp. All measurements were carried out in purified water, produced from a Millipore Element A10 system (Billerica, MA), with a resistivity of 18.3 MΩ/cm. Temperature-dependent FM-AFM imaging of DPPC was performed by heating the sample and collecting height images at 24°C, 50°C, and 60°C. FM-AFM frequency shift measurements were taken on both gel (24°C) and fluid (60°C) phase DPPC bilayers, and on fluid (24°C) DOPC bilayers. Imaging was also conducted immediately before and after taking frequency shift measurements. This ensured that the measurements were only performed on the bilayers and a number of suitable positions that were void of defects or contamination. Force measurements for each of the membrane samples (i.e., DOPC, DPPC (24°C), and DPPC (60°C)) were taken with six different CNT probes, and numerous curves were taken for each cantilever and at different positions on the lipid sample. The oscillation amplitudes used for the force measurements ranged from 0.8 to 3.2 nm and were determined by performing an amplitude force curve on a hard surface after the experiments to calculate the dynamic sensitivity of the cantilever, or could be determined using our recently developed “non-contact” technique (36).

Molecular resolution of lipid bilayers

Molecular resolution imaging of gel phase DPPC lipid bilayers in pure water was achieved using the FM-AFM technique with a different, ultra-low noise AFM, which only operates at room temperature. The instrument was designed according to previous work that used thermal limited noise performance and increased force sensitivity with a deflection noise density of 17 fm/√Hz (37). Modifications mainly involved limiting electrical noise and improving the performance and stability of the laser diode in the optical beam deflection system. These modifications have resulted in the capability of routinely achieving true atomic resolution of mica in liquid (38). Images were obtained with ≈46 N/m cantilevers (Q = 6.9 in water) using amplitudes ranging from 0.14 to 0.2 nm. Lipid samples were prepared as described above and imaged at room temperature. The ability to resolve the individual molecular headgroup structure and packing arrangement clearly demonstrated the high sensitivity of the FM-AFM technique for imaging and measuring short-range forces in liquid on biological samples.

RESULTS AND DISCUSSION

Highly sensitive frequency modulation AFM force measurements

Highly sensitive force measurements between CNT tips and lipid bilayer surfaces were performed using constant amplitude FM-AFM. In the force measurement mode, changes in the cantilever resonant frequency that occurred in response to an interaction force were recorded, as the oscillating tip approached and retracted over a single x-y position on the lipid bilayer. The frequency shift curves reflected the force profile of the interaction and could subsequently be directly quantified into a force (25). By optimizing the lipid concentration, we ensured that all force measurements were performed only on single lipid bilayers supported directly on the mica. Before force measuring, we imaged the bilayers using FM-AFM and then located the probe with nanometer accuracy at various selected points on the image. Finally, we also imaged during the experiments to ensure we were still on the lipid surface and that no damage had been done to the tip and sample.

Oscillatory forces above gel phase DPPC bilayers

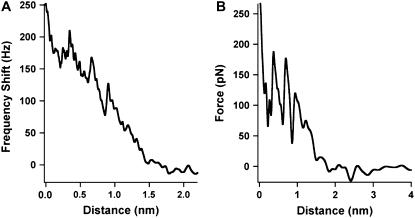
For gel phase membranes (24°C), frequency shift curves showed a continual increase in the frequency that indicated the presence of a background net repulsive force (Fig. 5 A). Wong et al. (39) showed that shortening of a CNT using an applied bias voltage, as done here, resulted in the end of the CNT becoming oxidized and terminated with carboxyl groups (COOH). Thus, it is possible that this background term may arise from hydrophilic forces, which have dominated over the also present double-layer and van der Waals forces (17). Alternatively, we observed a monotonic increase in the corresponding dissipation curve (data not shown), which, it has been suggested, correlated with impacting on a stiffer arrangement of water molecules near the surface (14). Significantly, 30.9% of the curves (n curves = 776) showed a number of clear oscillations with spacing approximating to the size of a water molecule superimposed on the background term (Fig. 5 A). Fig. 5 A shows a frequency shift curve with three oscillations each recording a range of ≈50 Hz. A corresponding converted force curve is shown in Fig. 5 B, where the force profile is effectively determined by the gradient of the frequency shift. Conversion of the frequency shift curve to a quantitative force clearly revealed the oscillatory nature of the hydration force that spanned a few hundred piconewtons (Fig. 5 B), with each oscillation recording a range of ≈100 pN. These oscillations indicated the molecular ordering of individual water layers between the tip and lipid surface and their subsequent displacement from between the two approaching surfaces. Each rise in the oscillations was due to an increase in the finite stiffness of the ordered layers until at the peak maximum the force was sufficient to displace a single layer.

FIGURE 5.

(A) Frequency shift curve for gel phase bilayer (24°C) reveals three oscillations superimposed on a background repulsive interaction. (B) Corresponding quantified force curve from the frequency shift using Eq. 1.

Periodicity and normalization of oscillatory forces

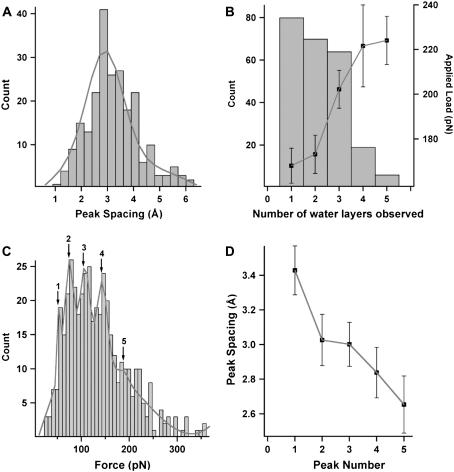
Due to the high reproducibility of the measurements, the peak spacing between the oscillations could be used to build histograms (Fig. 6 A). Our mean peak spacing value of 2.90 ± 0.06 Å (mean ± SE; n = 226) compared well to the approximate dimensions a water molecule and confirmed the structuring of water layers between the tip and bilayer surface. This value compares well with previously measured values for water layers next to various substrates (2.5–2.9 Å (16), 2.2 Å (14), 2.3 ± 0.03 Å (18), 1–3 Å (15)). The peak spacing has previously been shown to decrease in the vicinity of the surface (19), thus it is not determined solely by a constant value of the molecular diameter. A stronger attractive interaction with water layers near the surface has been used to explain smaller peak spacings (i.e., less than water molecule diameter), whereas larger values may be related to less tightly packed layers as they extend further out. In some cases, we recorded much larger values that were difficult to assign a physical interpretation. We suggest that these larger values may arise when the tip has missed a water layer or if there is thermal drift of the piezo perpendicular to the surface.

FIGURE 6.

(A) Histogram for the peak spacing between all oscillations from the total number of quantified force curves. Line curve shows Gaussian fit to peak spacing distribution (median = 2.9 Å, σ width = 0.4). (B) Histogram for the number of oscillations (i.e., number of water layers) observed in each frequency shift curve as a function of the average applied load. Error bars represent mean ± SE. (C) Histogram of the maximum peak force for all oscillations in the total number of measured curves. Multipeak Gaussian fit (line curve) reveals quantization of the forces occurring at 54.6 pN (peak 1, σ width = 3.6), 75.1 pN (peak 2, σ width = 5.1), 108.4 pN (peak 3, σ width = 6.4), 143.5 (peak 4, σ width = 5.4), 189.0 pN (peak 5, σ width = 41.9). (D) Peak spacing plotted as a function of a nominal force range around the quantized values indicated by peak numbers from the histogram in panel C, where peak numbers 1–5 have force ranges of 0–64 pN, 64–91 pN, 91–126 pN, 126–166 pN, and >166 pN, respectively. The average values between the quantized force values were used to nominate the upper or lower bound values of the corresponding force range. Errors bars represent mean ± SE.

Forces normalized for the CNT tip radius ranged from 1–20 mN m⁻¹ and were at the lower end of the range of 1–100 mN m⁻¹ previously measured for water on self-assembled monolayers (13,14,18). Normalizing the force by the probe radius has shown to be effective for CNT probes, as it has previously been shown that normalized oscillatory forces for OMCTS on graphite and water on SAM obtained using CNT probes were in agreement with forces measured using other techniques (i.e., SFA) (19,28). We emphasize that these oscillatory forces were not due to a “punch-through” effect (i.e., penetration of the tip into the bilayer) previously observed for gel phase DPPC bilayers. The maximum applied loads normalized by the CNT probe radius (≈20 mN/m) were ≈10 times smaller than the normalized forces (230 mN/m) required for observing a “punch-through” effect for gel phase DPPC bilayers in pure water using AFM (40). Furthermore, the force required to displace the first water layer (i.e., the first oscillation observed) was ≈50 times smaller than the “punch through” force. In addition, a measured z-distance of 4.3 nm for the “punch-through” effect (there is only one “punch-through” measured for a single bilayer) corresponded to the thickness of the single bilayer that was penetrated (40) and does not correlate with the angstrom length-scale of the water layers and multiple oscillations observed here.

Number and arrangement of water layers

Fig. 6 B shows a histogram for the number of oscillations observed in each curve as a function of the corresponding applied load, or in other words how closely the probe approached the sample. This data is compiled from an approximately equal number of curves taken over a range of applied loads and indicated that there was a tendency for the number of water layers observed to increase with an increase in the applied load. Higher counts for observing one, two, and three layers indicated that these were more commonly observed and occurred over a larger range of applied loads. In contrast, 4 or 5 layers were less commonly observed, suggesting that the structured water layers were reaching the limit of how far out they could extend.

Analyzing the properties of the water layers as a function of their relative distance was performed by plotting a histogram of all individual oscillatory forces at the peak maximum to reveal a quantization of the forces (Fig. 6 C), as indicated by the five peaks. This demonstrated that individual water layers categorize into discrete forces that can be directly related to their relative position from the surface due to the decreasing dependence on the oscillatory force with increasing separation. In this case, peak 1 corresponds to layers furthest away from the surface and requiring the least displacement force, whereas peak 5 corresponds to the layers closest to the surface that are much harder to displace. Using this classification, we observed that the peak spacing decreased with an increase in peak number (Fig. 6 D), suggesting a tighter packing of layers in close proximity to the surface most likely due to a strong attractive interaction between the water molecules and lipid headgroups. This layering effect was previously observed for AFM measurements of water next to a SAM (19).

Molecular resolution imaging of individual DPPC headgroups

Due to expected atomic-scale variations at the end of the CNT probe, we performed frequency shift measurements using a number of different tips. In doing so, measurements from all tips revealed oscillations and the total number of curves showing oscillations (≈30%) was significant. We suggest that based on height images obtained using our ultra low-noise FM-AFM that additional variations in the curves may arise due to slight lateral variations across the lipid surface, as indicated by the numerous higher (lighter) and lower (darker) regions in Fig. 7 A. Interestingly, a higher resolution 10 × 10 nm scan of an area in Fig. 7 A revealed a true molecular resolution image of the gel phase DPPC bilayer surface, which showed individual headgroups (bright spots) of lipid molecules hexagonally packed with a measured intermolecular spacing of 0.51 nm. The intermolecular headgroup spacing was obtained using an averaged Fourier transform value from four separate images. Similarly, angstrom-scale lateral variations across the lipid surface were observed in Fig. 7 B, which again may have influenced the number of curves showing oscillations. Due to these apparent small-scale lateral variations across the lipid bilayer surface, the frequency shift measurements were taken at different positions on an image. It is noted that these images were taken in light intermittent contact mode using FM-AFM and the frequency shift as feedback, thus the applied force on the sample was minimal.

FIGURE 7.

(A) 25 × 25 nm height image showing lateral-scale variation across the bilayer surface. (B) 10 × 10 nm higher resolution image clearly showing individual headgroups of lipid molecules hexagonally packed with an intermolecular distance of 0.51 nm.

Advantage of dynamic AFM and FM-AFM for oscillatory force measurements

To have high force sensitivity and detect forces less than ≈100 pN, the static AFM mode must utilize low spring constant (typically <100 pN/nm) cantilevers. The use of such cantilevers leads to a mechanical instability, which makes the tip “snap” toward the surface when the gradient of the attractive force exceeds the stiffness of the cantilevers. In our case, the gradient of the downward part of an oscillation (or attractive region) is ∼1000 pN/nm and thus is much larger than the cantilever spring constant value required for these measurements. When the cantilever “snap in” occurs no data is recorded in the attractive region of the curve and it is likely that over length-scales of a few angstroms the measured force profile will actually resemble a staircase pattern. In some cases, this force profile over such a small length-scale would be difficult to distinguish from a pure monotonic profile in the presence of deflection noise. Dynamic mode AFM avoids this limitation by using stiffer cantilevers and provides the true force profile, but at the same time maintains high force sensitivity. Thus due to the above advantages, dynamic AFM techniques such as amplitude and frequency modulation have been used to study oscillatory forces of confined liquids.

FM-AFM was also able to resolve the true oscillatory profile even when the even when the oscillation amplitudes used (i.e., 0.8–3.2 nm) were 3–10 times higher than the 2.9 Å water molecular diameter. This situation is possible because measuring a change in the resonance frequency allows for high sensitivity to the interaction force, even when the amplitude is larger than the length-scale of the interaction. For small amplitudes that are comparative to the interaction length-scale (i.e., water molecule diameter), the force is sampled over a larger portion of the oscillation amplitude. This results in a greater frequency shift and higher sensitivity. In contrast, for larger amplitudes the same interaction force is sampled over a smaller proportion of the oscillation amplitude, nearer the bottom of the cycle. Importantly, this still allows for the detection of a frequency shift or force, though its magnitude is smaller and thus, so too is the sensitivity. Eventually, a limit is reached for the amplitude where the frequency shift will become undetectable. Much of the earlier atomic resolution imaging and force measurements performed using FM-AFM in UHV employed the use of larger amplitudes (41). We have also shown in earlier work that oscillatory forces for OMCTS (8 Å) and water (2.5 Å) could be detected using amplitudes that were ∼10 × larger than the molecular diameter (19,28).

DPPC and DOPC fluid phase bilayers disrupt oscillatory forces

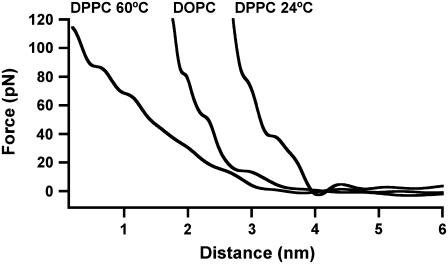
For DPPC fluid (60°C) phase bilayers, <1% of the frequency shift curves (n curves = 574) showed oscillations that were discernable above the noise level and these curves recorded lower force values than previously observed on the gel phase. Although it appears that DPPC fluid phase bilayers disrupts the oscillatory force, it is difficult to separate out the possible effect of temperature. This was addressed by performing measurements on DOPC which has the same lipid headgroup as DPPC, but a lower transition temperature of −20°C making it fluid at room temperature. FM-AFM measurements on these bilayers revealed that only 3.5% of the curves showed oscillations (n = 705), also with lower forces, indicating that membrane fluidity had a direct effect on disrupting the oscillations. Fig. 8 shows typical force curves for DPPC at 60°C and DOPC (24°C) showing no oscillations and a similar curve of DPPC (24°C) for comparison. Possible explanations for the absence of oscillations on the fluid phase are 1), that the increased thermal motion and surface roughness of the lipid headgroups smear out the oscillatory force leaving only a monotonic component; 2), in the fluid phase there are a considerable number of molecular degrees of freedom in the highly thermally excited headgroups and an expected increase in the molar volume per lipid. A subsequent decrease in the density of the headgroups on the surface may expose the melted hydrophobic tails and as such, this change in chemistry may perturb the structure of the adjacent water molecules, and 3), the length of the repulsive region for the fluid phase membranes were larger compared to the DPPC gel phase (Fig. 8), indicating the fluid phase was more deformable. An increased surface deformability of the fluid phase membrane will reduce the measured oscillatory force at a given separation, but alone should not account for an absence of any oscillatory force. In this case, a higher sensitivity and lower noise detection system may be required to detect the smaller oscillatory forces.

FIGURE 8.

Typical quantified force curves for DOPC (24°C) and DPPC (60°C) showing no oscillations. A similar curve for DPPC (24°C) is shown to compare the length of the repulsive region for each membrane at an applied load of 120 pN.

Oscillatory forces on lipid bilayers: confinement or hydration?

These findings clearly showed that the nature of the force required to displace up to five structured layers of intervening water molecules confined between a nanometer-sized probe and biological membrane is indeed oscillatory. To obtain an oscillatory profile, the water layers must be removed in a discrete way from between two surfaces. This may not necessarily occur even when an oscillatory density profile is present at only one of the surfaces, thus it is important to appreciate the difference between an oscillatory force and a measured oscillatory density profile next to an individual surface (42). Importantly, we have shown here that an oscillatory force on the nanoscale does exist when one of the two surfaces involved is a lipid bilayer. The ability for the DPPC lipid bilayer to promote an oscillatory force is highlighted by the bilayer stability that allows for molecular resolution imaging of the individual headgroups (i.e., the bilayer is relatively stiff)). In addition, the well-ordered hexagonal packing of the headgroups, as opposed to a randomly rough surface, would allow for an oscillatory force (43). From the measurements, it cannot be determined if the structured water arises from an induced confinement effect between the AFM probe and bilayer, or whether they are inherent hydration layers at the lipid and/or CNT probe surface. However, there is emerging evidence for the ordering of water layers at the surface of lipid bilayers. Berkowitz et al. (44) used simulations to calculate the water density profile next to a DPPC membrane surface to investigate whether there was an oscillatory character reflecting the hidden packing arrangement of water molecules. These researchers found that the water density profile did show oscillations that indicated the presence of one or two layers extending from DPPC lipid headgroup. Using Coherent anti-stokes Raman scattering microscopy (CARS), Cheng et al. (45) revealed that water molecules close to the phospholipid bilayer surface were ordered with the symmetry axis along the direction normal to the bilayer. In addition, the amount of ordered water molecules depended on the lipid polar group. Molecular dynamic simulations showed that in addition to one to two water layers directly solvating DPPC lipid surfaces, there were extra water molecules present within interbilayer spacings which may be involved in the hydration force (9). As there were a significant number of layers observed here (i.e., five layers), it is possible that both confinement and hydration effects may contribute to the formation of these structured water layers.

Oscillatory forces and implications for cell membrane theory

Irrespective of the origin of the water layers, our results here provide new information to describe the forces that may be encountered by a molecule approaching a cell membrane. For example, in the case of only a purely monotonic repulsive force, either due to electrostatic or hydration forces, the cost of free energy required for a molecule to approach from the bulk liquid to the membrane is governed by a gradual rise in the force and is given by the area under the force curve. In contrast, for the oscillatory profile, because there is a continual rise and fall in the force due to the sequential displacement of individual water layers, the area under the curve is the energy required to bring the molecule and lipid together in addition to the amount which would be required if the repulsive force was simply monotonic. Thus, the total cost of energy on the molecule over the entire interaction is greater. We calculated that the cost of energy required to displace a single water layer using a probe with cross-sectional area of 300 nm² is 8 × 10⁻²⁰ J (≈20 k_BT). This energy will be additive for multiple water layers.

The comparison of gel and fluid phase bilayers in this study is highly relevant, as emerging fluid mosaic models of the cell membrane which show that among the diverse lipid composition (≈500–1000 different kinds of lipid), with varying structure and temperature phase transitions, there are lipid patches or domains which differ from the average of the bilayer. Experiments show that gel-fluid phase separations exist, as well as phase separations for immiscible fluid lipids, whereas domains have also been detected on whole cells (46). A “lipid-raft” model has been proposed to suggest that domains function as regions for trafficking of lipid-proteins and molecular signaling platforms (47). For the fluid phase bilayers here, the multiple energy barriers associated with the water layers mostly disappear, suggesting a disruption of the structured water. Indeed, cellular regulation of membrane lipid composition may be important for controlling hydration in the immediate proximity of the cell surface and consequently influence the function of different regions of the heterogeneous membrane, such as permeation (48). In eukaryotic cells domain coexistence is believed to result from liquid-disordered and liquid ordered phases (46). Interesting future work could involve investigating the water layers near mixed lipid phases in the presence of cholesterol (e.g., POPC/cholesterol/sphingomyelin), or native cell membranes/living cells. Our current findings are of fundamental significance for short-range biological interactions as they highlight the importance of considering water structure as an integral component in cell membrane theory and should also be considered in related processes such as drug design (49).