Kinesin's Biased Stepping Mechanism: Amplification of Neck Linker Zippering

Abstract

A physically motivated model of kinesin's motor function is developed within the framework of rectified Brownian motion. The model explains how the amplification of neck linker zippering arises naturally through well-known formulae for overdamped dynamics, thereby providing a means to understand how weakly-favorable zippering leads to strongly favorable plus-directed binding of a free kinesin head to microtubule. Additional aspects of kinesin's motion, such as head coordination and rate-limiting steps, are directly related to the force-dependent inhibition of ATP binding to a microtubule bound head. The model of rectified Brownian motion is presented as an alternative to power stroke models and provides an alternative interpretation for the significance of ATP hydrolysis in the kinesin stepping cycle.

INTRODUCTION

Conventional dimeric kinesin (or just kinesin, see Figs. 1 and 2 for a basic overview) is a microtubule-based molecular motor, which, despite extensive study, has left several unanswered questions regarding its fundamental mechanism of forward motion. Noteworthy in these is the bias problem: that a small neck linker zippering free energy of a couple of k_BT generates a thousand-fold favorability (i.e., bias) to step forward rather than backward (1). A reduced but still substantial forward bias persists at loads of several picoNewtons (2), and at these loads, neck linker zippering moderates mechanical work many times larger than the zippering free energy. This amplification of zippering is not consistent with a power stroke model for kinesin. Indeed, zippering as a power stroke would necessarily imply large zippering energies that no longer require amplification.

FIGURE 1.

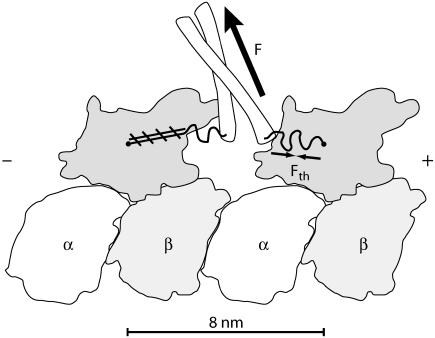
A doubly-bound kinesin dimer oriented with the microtubule plus-end to the right. The N-terminal kinesin heads can bind to tubulin (36,41–43). The kinesin heads are connected by two neck linkers, ∼15 amino acids each (4), and these neck linkers end in a coiled-coil “stalk” that can connect cargo through light chains and mediate tension, indicated by F (the load force). Entropic considerations for the neck linkers suggest a thermal force, F_th, which resists neck linker extension. A microtubule-bound head in an ATP or hydrolyzed ATP (ADP.P) state will initiate immobilization (zippering) of its neck linker onto itself through a series of hydrogen bonds, schematically indicated by hatched lines. This figure outlines structures found in Protein Data Bank file: 1IA0 (43).

FIGURE 2.

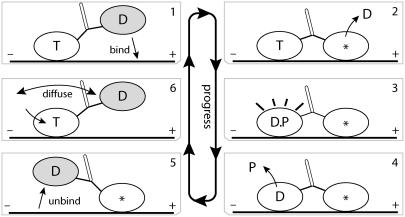
Key aspects of kinesin's forward (plus-end) cycle have been elucidated through a varied multitude of experiments, including cryo-EM, x-ray structural, force bead, and others (4,12,23,44–48). This process is briefly reviewed, where T labels the ATP nucleotide state, D the ADP nucleotide state, * the no-nucleotide state, and P the phosphate after ATP hydrolysis. The free head is shaded to clarify motion between frames. Frames 1,2: the free head weakly binds to the plus-end binding site, leading to strong binding once ADP is released. ATP binding to the plus-end head is inhibited by a coordinating mechanism (labeled T-gate; see subsection T-Gate) that is activated by the internal strain. Frames 3–5: hydrolysis of ATP in the minus-end head leads to an intermediate ADP-phosphate state, D.P, and phosphate release alters the binding of the minus-end head into weak binding, which allows rapid release of the minus-end head from tubulin (14). Frame 5 is to be identified with the parked state in Carter and Cross (2). Frame 6: the free head tends not to strongly bind until ATP binds to the microtubule-bound head (34). ATP binding initiates zippering of the microtubule-bound head's neck linker, coinciding with a large acceleration of the rate for the free head to bind onto microtubule. This entire forward cycle consumes one ATP and moves the center of mass of the system ∼8 nm.

Kinesin's behavior emerges instead from an altogether different approach, built on the framework of rectified Brownian motion (RBM) (3–5). Central to RBM is that a microscopic cycle may harness large thermally driven displacements that are in turn made irreversible by the expenditure of free energy at the boundaries of this diffusional process (e.g., at binding sites). The boundaries thus irreversibly drive an otherwise reversible system (6). This shift in emphasis from the direct forcing of an active element to the harnessing of diffusion embodies an appreciation for the overwhelming friction and thermal noise characteristic of kinesin's very low Reynolds-number environment (7–9). Very low Reynolds number practically necessitates the utilization of diffusional motion when kinesin's geometry is considered. Such considerations were incorporated early in the investigations by Peskin and Oster (10), though their modeling, which was done before the revelation of neck linker zippering, concluded that diffusion was secondary to power stroke contributions.

Our RBM model supposes that the diffusional displacements of a tethered head are rectified by the irreversible binding of this head to microtubule, reminiscent of Huxley's diffuse-and-latch scheme for muscle contraction (11). Mechanical work against an external load is then a result of the ATP free energy expenditure associated with binding, rather than zippering. The bias problem is neatly dispatched by this shift in emphasis. Using small zippering free energies and physically motivated components, our model establishes a fast biasing mechanism that determines the stepping bias at a given load. This biasing mechanism amplifies neck linker zippering through surprisingly little else than the naturally existing internal strain between kinesin heads.

Complementary to the biasing discussion of the article, kinesin's rate of stepping along the microtubule is briefly addressed. Emphasis is placed on a recently discovered force-dependent gate (labeled “T-gate” here) that controls ATP binding to a microtubule-bound head (12–14). The role of T-gate originally arose in the chemical coordination between the two heads of a kinesin dimer, but T-gate, taken loosely as the entire mechanism for ATP uptake, also subsumes responsibility for the rate-limiting behavior that arises at both low [ATP] and high external loads. The effect of T-gate is to ultimately establish a “waiting mechanism” that controls dwell times (the time between measured displacements of kinesin along a microtubule).

The article is organized as follows. Structural and Chemical Functional Elements, through several subsections, outlines key physical components of the kinesin dimer and their respective modeling. With these components, a simplified discussion that exemplifies the origin of bias is presented in Basic Biasing Mechanism and the Heuristic Model of Bias, including both a general argument and a specific numerical example. Key principles in this section are then extended to a detailed model of kinesin's bias in Biasing Mechanism (Appendix A contains the actual model development). Discussion of kinesin's cycle is completed in Waiting Mechanism, with the development of a waiting mechanism that generates dwell times. Concluding remarks occupy Conclusion.

STRUCTURAL AND CHEMICAL FUNCTIONAL ELEMENTS

Experiments have isolated several components that participate in kinesin's forward cycle. Our model incorporates a number of these components through simplified representations that are appropriate for our level of detail. Here, the more involved discussion of our model is preceded with several brief treatments of the elements in kinesin's modeling.

Neck linkers and the coiled-coil neck

Of central importance to the understanding of kinesin's cycle are the elements that connect the two kinesin heads, namely, the two nonrigid neck linkers that together merge into a fairly stable coiled-coil neck (4). The coiled-coil was originally supposed to provide, through its unwinding, an essential ingredient for the existence of kinesin's forward motion, but experiments do not support such a theory (15). Neck linkers are then assumed to provide the leading functional contributions, in part by forming entropic springs that generate a force by virtue of thermal fluctuations alone. These entropic springs supply an “internal strain” that guides kinesin's functioning (14), e.g., by coordinating chemical states through activation of T-gate (see the subsection T-Gate, below).

For the neck linker entropic force, a model from the study of polymers will be called upon to approximate our ∼12–15 amino-acid neck-linker chain. Though the length of a neck linker is far removed from the length of most polymers, the 12–15 neck linker units may already be sufficient for common polymer statistical mechanical chains models to apply when fluctuations are included (e.g., the variance of extension for a forced, diffusing neck linker is allowed to be comparable to the mean extension). The most appropriate standard model for a peptide backbone is the freely-rotating chain (16), due to the axial nature of peptide bonds (if the bond angle is very small, then results are known as the wormlike chain, i.e., WLC (17,18)). Instead, an effective freely-jointed chain (FJC) model is used for the sake of simplicity (16,19). The reduction of a chain force to an effective FJC or WLC is not uncommon, e.g., for DNA (20).

A computationally friendly form of the FJC force model utilizes a rational polynomial approximation that gives the correct asymptotic results for large and small extensions of length x (21),

(1)

where α is the relative extension x/Na, a is a link length for one amino acid, N is the number of amino acids in a neck linker, and η is a fitting parameter to set the correct linear regime dependence. The linear regime force constant, 3η k_BT/Na², can readily scale to several picoNewtons per nanometer for parameters describing peptide bonds. The x-integral of this force function provides a free energy potential that defines the single-chain Boltzmann probability density, ρ_N,

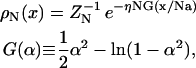(2)

where Z_N is a normalization constant. Expected values for the model parameters are η of order unity and the virtual peptide bond length a ≈ 0.38 nm (compare to a = 0.35 nm for the axial distance per amino acid in a β-sheet).

Though coiled-coil unwinding was not found essential for the forward motion of kinesin (15), steric aspects of the coiled-coil and its unwinding contribute substantially to bias calculations. Our modeling assumes that the width of the coiled-coil (possibly partially unwound) provides a given length Δd to the head-to-head extension in addition to the neck linkers. Acting upon the one-dimensional representation to be used for kinesin's diffusive step (akin to a reaction coordinate; see Basic Biasing Mechanism and the Heuristic Model of Bias, and also Appendix A), the coiled-coil prompts modeling of the tethered head's diffusion within an effective reduced interval, [−d, d] = [−d₀ + Δd, d₀ − Δd], where d₀ ∼ 8.2 nm is the original binding distance. This reduced interval minimally accounts for the extra reach due to the width of the coiled-coil. Notice that though the coiled-coil extension in the real system will dynamically change in response to entropic neck linker forces, this time-dependent effect is ignored in our model. Our model similarly ignores the restoring force due to coiled-coil unwinding (a static element that produces no intrinsic force).

Neck linker zippering

Estimated only to possess a free energy difference of ∼2 k_BT (1,22), neck linker zippering is surprisingly essential for kinesin's processive motor function (4,23,24). Our modeling of neck linker zippering borrows from work done in protein folding, specifically the formation of β-hairpins. From statistical-mechanical investigations, β-hairpins exhibit bistable cooperative behavior due to competition between hydrogen-bond formation and the configurational entropy of a solvated chain (25–27). This bistability inspires a finite two-state zippering model (the kinematics are made more precise in Appendix A), where the state with several formed hydrogen bonds is labeled the “zippered” state, and the absence of zippered bonds is labeled the “unzippered” state.

The basic purpose of zippering is to immobilize neck linker links in the microtubule plus direction, thus shifting the anchoring point (point of emanation) for the microtubule-bound head's neck linker toward the forward binding site. Supposing that N_z is the number of immobilized links in the zippered state, the act of zippering is modeled by a change that simultaneously shifts this anchoring point a plus-directed distance Δx = N_za and reduces the number of solvated neck linker links for the microtubule-bound head by N_z.

Since the external load will tend to place a strain on the neck linker, a Bell form (28) is taken for the Boltzmann probability of being in the zippered state (probability P_z) versus the unzippered state (probability P_u),

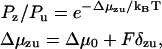(3)

with Δμ_zu the free energy of zippering, Δμ₀ the free energy at zero load, F the external load, and δ_zu the characteristic distance for zippering. Our model takes δ_zu = γN_za, with N_z the number of zippered links, a the link length, and γ as a pure number. For γ = 1, δ_zu is then the length of the zippered segment.

At biological temperatures, F_zu = k_BT/δ_zu defines a characteristic force of F_zu ∼ 2 picoNewtons if δ_zu ∼ 2 nm (approximately five zippered neck-linker links). Zippering then remains forwardly biased for loads up to ∼4 pN for zippering energies of magnitude 2 k_BT. Reaching this force does not necessarily imply that kinesin has stalled, since a small probability to be in a zippered state can be sufficient for an overall forward bias (see Basic Biasing Mechanism and the Heuristic Model of Bias for an explanation of this, as a result of the amplification of bias).

Weak binding

When a kinesin head is in the ADP nucleotide state, the bonding strength of the head with tubulin is observed to be markedly lower than in other states, and consequently, the microtubule-bound ADP state has been labeled weak binding (strong binding has higher bonding strength and is associated with the ATP and no-nucleotide states). Measurements were done by Uemura et al. (29,30) to determine weak state unbinding rates when a weakly bound head is under external forcing, finding that a natural forward bias exists in weak state unbinding. Our model uses a more symmetric form of weak state unbinding rates that is directionally independent,

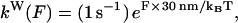(4)

with F the applied force magnitude. Equation 4 approaches the rates of other internal processes, e.g., 150 s⁻¹, when F ∼ 7 pN. Such forces are attainable with entropic neck linker tensions.

T-gate

Chemical coordination between the heads of a doubly-bound kinesin dimer has been linked to internal strain activating a gate (T-gate) that prevents the binding of ATP to the plus-end head (12–14). This coordinating mechanism allows the forward head to remain in the no-nucleotide state until the rearward head releases phosphate and detaches, thereby relieving the rearward force on the forward head and allowing ATP to bind. Without this coordination, kinesin would be unable to take more than a few steps before dissociation. T-gate thus establishes an important link between mechanical forces and chemical rates.

Further effects of T-gate are discussed in Waiting Mechanism, within the context of the waiting mechanism.

BASIC BIASING MECHANISM AND THE HEURISTIC MODEL OF BIAS

Kinesin's stepping bias is derived from the probability for the tethered kinesin head to strongly bind either forward or backward once ATP has bound to the microtubule-bound head. Appeals to stochastic simulations of the full kinesin system, involving the diffusion and interaction between kinesin's elements (such as those in Structural and Chemical Functional Elements), could then provide this stepping bias. However, the underlying principles that drive kinesin may be lost in such an approach. A more analytical treatment is instead taken in this article, proceeding from a general argument for the origin of kinesin's bias to the justification of this argument through two specific models of increasing detail.

The general argument behind the theory of kinesin's stepping bias supposes only the basic aspects of kinesin's structure and neck linker zippering. Foremost and most intuitive in the argument is that the likelihood of a tethered kinesin head to bind either forward or backward is directly related to the frequency (probability) for this head to visit each respective binding site. This visitation probability may be predicted by the free energy Boltzmann factor that corresponds to system configurations with a kinesin head near a given binding site (this approach is similar to that in transition-state theory). Assuming a large internal strain between the kinesin heads when they are separated, e.g., by the entropic neck linker force, the configurational free energy Boltzmann factor depends exponentially strongly on head-to-head separation. Accordingly, visitation probabilities are also exponentially sensitive to head-to-head separation.

Exponential dependence of the visitation probabilities near binding sites becomes relevant with the consideration of neck linker zippering effects. Suppose, as described in Neck Linker Zippering, that a small shift in the tethered-head probability density toward the microtubule plus-direction results when the neck linker is in the zippered state. The required energy to ensure this shift against an applied external load is accordingly small up to a limiting load value, such that zippering itself remains a weak effect. In combining exponentially sensitive visitation probabilities with neck linker zippering, exponentially large changes in stepping bias are the result (a mathematical version of this statement appears later in this section as Eq. 9). In short, the main result of this article is that internal strain sensitizes kinesin to the small changes due to zippering.

A critical, though often ignored, feature of the above biasing argument is the implicit assumption that binding and unbinding are essentially irreversible (involving the large free energy expenditure associated with strong binding transitions and ATP hydrolysis). This free energy ensures a strongly forward arrow of time in kinesin's stepping cycle (31), i.e., free energy ensures that the time-reversed version of kinesin's cycle rarely occurs. The opposite assumption of totally reversible binding transitions would invalidate our argument for the origin of kinesin's bias, since free energy-work principles would require that zippering energy be the sole source of work against an external load. For example, premature unbinding of a forward head may become problematic if binding is reversible. Thus, kinesin's strong forward bias, and also any associated mechanical work, is energetically a bound-state effect more than a zippering effect. This observation is what qualifies kinesin as an RBM mechanism. A note of caution may be warranted at this time: irreversibility is measured at the level of an entire cycle, rather than any single step (32). The statement that irreversibility arises primarily through binding is in the context of the cycle as a whole.

Explicit justification of the above argument is here made for a simple kinesin-like heuristic model, as a prelude to a more complete description. The role of neck linker zippering in the amplification of stepping bias arises analytically as an exponentially catalyzed forward stepping rate associated with the zippered neck linker state. This catalysis of forward binding leads to the clear identification of a bias amplification factor that multiplies the naive bias estimate (the Boltzmann factor of the zippering energy) to produce the actual stepping bias.

Before construction of the heuristic model, the reader is reminded of the results of Kramer's escape rate theory as a means to determine binding rates. Kramer's theory supplies the rate, k, for the transition across some abstract boundary, providing that the value of the free-energy barrier ΔU required to reach that boundary is known. That is,

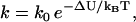(5)

where k₀ depends on the system parameters subexponentially. Assume that there exist forward and backward points of escape (i.e., binding), at which the free energy barriers U_f and U_b, respectively, are known. Using Eq. 5, the ratio ξ of forward to backward rates is

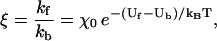(6)

where the subexponential dependence has been factored into χ₀. Equation 6 reflects the previously mentioned correspondence between stepping bias and visitation probabilities (i.e., configurational free energy Boltzmann factors) for forward and backward binding sites.

The structure of this heuristic model reduces to a knowledge of the free energy profile and the location of binding sites. A function U(x) is identified with the free energy for kinesin in the unzippered state to have a given head-to-head extension x along the microtubule, where the one-dimensional signed coordinate x is positive for extensions toward the microtubule plus-end. The value U(x) is assumed to be an even function in x, where evenness is motivated by the expectation to find approximately neutral intrinsic stepping bias for an unzippered state (neck linker zippering would not be needed otherwise). In relation to the unzippered state, the zippered state free-energy function is given through a translation of the neck linker origin and the addition of the energy difference Δμ₀ corresponding to the zippering energy, i.e., U(x) → U(x − Δx) + Δμ₀. Translations are sufficient to introduce asymmetric favorability of the forward binding site, such that exponentially large biasing changes will appear. A translation only approximates the effect of zippering, since physically, zippering also alters the shape of U(x) by reducing the number of solvated chain links (see Neck Linker Zippering). Forward and backward binding are defined to occur at x = d and x = −d, respectively. The values U_f and U_b in Eq. 6 then correspond to evaluation of the potential energy at x = d and x = −d, respectively.

Application of Eq. 6 to this heuristic model construction follows. The rate to bind either forward or backward may be written as the sum of zippered (z) and unzippered (u) state contributions,

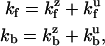(7)

where each rate in the sum is related to the evaluation of the probability density of either a zippered or unzippered state at x = ± d. Explicitly,

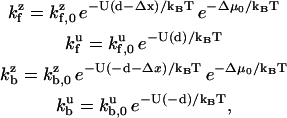(8)

where factors such as 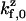differ from each other only subexponentially. Assuming that a Taylor expansion to first-order is valid in the exponential, i.e., U(d − Δx) ≈ U(d) − λΔx, the stepping bias may be written:

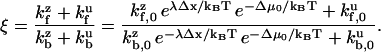(9)

Implicit in writing Eq. 9 are the simplifications involving evenness of U(x), oddness of 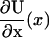, and the cancellation of terms 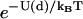in the numerator and denominator. Equation 9 includes the usual zippering energy Boltzmann factor 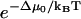and additionally includes the factor 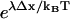associated with asymmetry of the binding site visitation probabilities for the zippered state. If the asymmetry factor is sufficiently large, Eq. 9 simplifies: 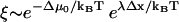, up to subexponential terms (the exponential factor in the denominator becomes vanishingly small while the exponential factor in the numerator becomes dominant). Thus, 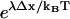may be interpreted as the amplification factor of the naive zippering energy Boltzmann term. The presence of bias amplification in Eq. 9 indicates that the stepping bias is not necessarily equivalent to the zippering energy Boltzmann factor.

Numerical values of the amplification factor can be readily estimated. The choice Δx = 2 nm is made for the zippering distance, corresponding to approximately five zippered neck linker links. The expression 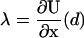is related to an effective internal strain of the system near the boundary. By consideration of entropic neck linker forces (Eq. 1), λ = 10 pN is chosen as an example of effective force. These values lead to an amplification factor of 130 at biological temperatures (ξ ≈ 1000 if Δμ₀ = 2 k_BT), which can substantially change predictions from the zippering energy Boltzmann factor alone.

The strength of the heuristic model is its simple presentation of the origin of bias. However, certain relevant elements of kinesin's cycle (e.g., weak state binding and unbinding) are ignored for the purpose of conceptual clarity. Biasing Mechanism and also Appendix A resolve these shortcomings with a more detailed consideration of kinesin's functional elements.

BIASING MECHANISM

The heuristic model of biasing in Basic Biasing Mechanism and the Heuristic Model of Bias can be expanded into a detailed model that considers carefully the roles of weak binding, zippering, and entropic neck linker forces. Elaboration on the structural and mathematical details of this biasing mechanism are found in Appendix A. Conclusions of this detailed model are similar to earlier assertions: that the rate for the diffusing head to weakly bind during the biasing mechanism is proportional to the stationary probability density p_s for this head in the vicinity of the binding site (see Eqs. 5, 11, and 19), and that the stepping bias ξ(F) at load F generally also depends on weak state unbinding rates (see Eqs. 4 and 20). A convenient numerical observation, that the biases ξ(F) for physically relevant parameters satisfy an approximate Bell form (as in experiment (2,33)), allows a parameterization of ξ(F) in terms of the zero-load bias and stall force. In this manner, all provided examples of this section are selected to match the “measured” bias Bell form with a zero load bias of 1000 (i.e., 99.9% forward) and a stall force of 7.0 pN.

Two useful cases arise for the parameters of the biasing mechanism: those lacking and those retaining weak state unbinding. Elimination of weak binding effects in the former case emphasizes the diffusional origins of bias utilized by the heuristic model. To demonstrate specific solutions of the modeling parameters for both of these cases, example parameter sets that match the measured bias are presented below.

Both of these examples share the parameters T = 300 K, N = 13 (13 total neck linker links), a = 0.38 nm (virtual link length), d₀ = 8.2 nm (distance to the next binding site), Δμ₀ = −2 k_BT (zippering energy), and k^S = 300 s⁻¹ (the strong binding rate constant used in Eq. 20). The remaining parameters were made variable and matched to the “measured” bias Bell form with the construction in Appendix A: η (neck linker force constant in Eq. 1), N_z (number of zippered links in the zippered state), Δd (static extension of the coiled-coil in Neck Linkers and the Coiled-Coil Neck), and γ (a scaling parameter for δ_zu, the Bell length of zippering in Eq. 3). For the case lacking weak state unbinding, these are η = 1.4, N_z = 4, Δd = 4.6 nm, and γ = 1.0. For the case with weak state unbinding, these are η = 0.86, N_z = 5, Δd = 5.0 nm, and γ = 0.5. Other example parameter sets that match the measured bias certainly exist, but they are not explored here. Further details for the example lacking weak state unbinding are given in Fig. 3.

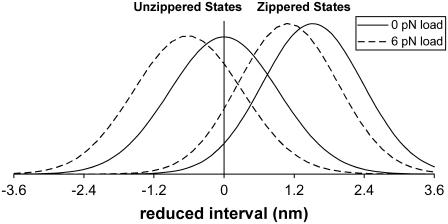
FIGURE 3.

Plots of zippered and unzippered stationary probability densities (in arbitrary units) versus the reduced interval [−d, d] (see Neck Linkers and the Coiled-Coil Neck and Eq. 11), for the case example in Biasing Mechanism that ignores the effects of weak state unbinding. The use of the reduced interval, which subtracts the coiled-coil extension, hides the fact that zippering is a small change (∼2 nm) compared to the distance traveled by one head (∼16 nm). Zippering probabilities, e.g., Eq. 3, are not represented in these plots. As discussed in Basic Biasing Mechanism and the Heuristic Model of Bias, the small and decreasing tails of the distribution are responsible for the generation of large biases. Apparent in these plots are the competing influences of zippering, which shifts the density toward the plus-end, and of loads, which shifts the density toward the minus-end. Stall occurs when all these effects balance one another. The inclusion of weak state unbinding in the model preserves many of the features presented here.

Evident in these numerical examples are the large predicted coiled-coil extensions. However, this observation may not translate well into the corresponding physical statement that large coiled-coil unwinding exists during the biasing mechanism. This problem arises due to the ignored restoring forces that are generated by unwinding of the coiled-coil, where these forces will alter bias calculations, e.g., via Eq. 9. Introduction of a force-extension model for the coiled-coil (not an entirely trivial task) would better address susceptibility of the coiled-coil to large extensions. Regardless of these technicalities, a 10-fold reduction in kinesin's processivity has been attributed to experimental stabilization of the coiled-coil (to prevent unwinding) (15), which indicates that some coiled-coil unwinding is natural in kinesin's normal forward cycle and should appear in modeling. Large Δd values may then be reasonable.

Results of our model also indicate that the biasing mechanism remains a fast step within kinesin's cycle as the external load is increased. Relevant to this is the rate for a diffusing head to weakly bind, with forward and backward binding rates 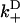and 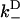, respectively. The most rapid rate of these at a given external load, i.e., max(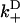, 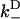), approximates the rate of the biasing mechanism's diffusional step. Numerical examples (e.g., the above examples) indicate that this maximum rate tends to not decrease by more than a factor of 20 at increasing loads—a factor small enough to leave the diffusional step relatively fast. In contrast, the diffusional bias 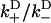undergoes larger changes through the combined effect of 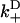decreasing and 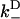increasing. Numerical examples further suggest that these observations are not drastically altered with the inclusion of weak state unbinding events.

The combination of entropic neck linker forces and weak binding states in this biasing mechanism provides an avenue for the exploration of the ADP gate discovered by Hackney (34). Hackney observed that in the combined absence of ATP (i.e., without zippering) and external load, the free head of a singly-bound kinesin dimer binds to microtubule only slowly, if at all. This situation is a “parked” state (2). Judging from similarities between the unzippered state in the biasing mechanism and this parked state, e.g., that each lacks neck linker zippering, Hackney's gate should be a consequence of long lifetimes for an unzippered-like state (compare to the unzippered zero-load state in Fig. 3). Long parked lifetimes in Hackney's experiment may then occur, for instance, if weak state unbinding becomes much faster than the strong binding rate k^S. The analysis of this approach is not done here, but this path to Hackney's gate remains attractive.

WAITING MECHANISM

The biasing mechanism of Biasing Mechanism is primarily suitable for describing the direction of stepping. Since biasing remains relatively fast, the dwell times for kinesin's cycle are rather taken to arise from the chemical steps that occur outside of biasing—collectively labeled the “waiting mechanism.” Some important technicalities in the logical separation of biasing and waiting are presented in Fig. 4. T-gate's mechano-chemical coupling is invoked as the principal contributor to the waiting mechanism at rate-limiting conditions, directly coupling the stress of an external load (in a geometry similar to frame 5 of Fig. 2) to the rate at which kinesin binds ambient ATP. Rate-limiting aspects of kinesin's cycle, at either high load or low [ATP], are then determined by ATP binding rates.

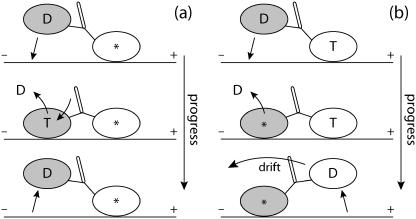
FIGURE 4.

Much of the biasing mechanism is assumed to occur in the parked geometry of frame 5 in Fig. 2, where the external load acting on the microtubule-bound head leads to long dwell times (see Waiting Mechanism). However, the free head could have, in the time before ATP uptake, an opportunity to bind rearward during a period when forward binding is virtually excluded (due to no zippering). Thus, bias would then be [ATP] dependent due to [ATP] dependence of the waiting mechanism. In panel a, a fast step is outlined that corrects this undesired backward stepping. Since the forward head experiences strain due to the rearward-bound head, ATP uptake is greatly inhibited in the forward head, and thus, there exists a much larger probability that the rearward head detaches first (at the expense of one ATP hydrolysis). In contrast, panel b outlines how a “real” backward step may occur once the waiting mechanism has ended, i.e., once ATP has bound to the microtubule-bound head. Notice that if the rearward head binds as in panel b, the forward head is at least one chemical step ahead of the rearward head. With a few assumptions, the forward head in panel b may then be expected to release first on average. Events in panel b where instead the rearward head unbinds will alter the simple relation between binding and stepping direction, but these (potentially uncommon) events are ignored at the level of detail in this article.

A common element in the numerous models for dwell times is a Bell length of magnitude 2–3 nm that is responsible for rate-limiting behavior at external loads of several picoNewtons (2,33). Supposing that T-gate indeed manages dwell times, then this Bell exponent characterizes the load dependence of T-gate. This identification is consistent in magnitude with the fact that T-gate's coordinating mechanism is activated by internal strain on order of several picoNewtons. A rate model, presented in Fig. 5, is based on the ansatz chosen for a natural lifetime within T-gate,

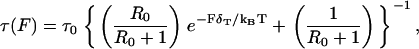(10)

with τ₀, R₀, and δ_T constants to be determined. Equation 10 is intentionally similar to Eq. 3 used by Nishiyama et al. (33), though Eq. 10 is an ad hoc way to implement a ceiling in T-gate's ability to inhibit ATP (e.g., due to higher loads altering the accessibility of the nucleotide pocket differently). The placement of τ(F) within our rate model is similar to Fig. 2 of Block et al. (35), with their k₋₂ set to zero. Additional details are in Fig. 5.

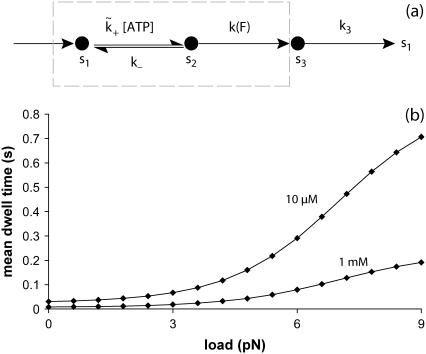
FIGURE 5.

Panel a illustrates a rate model to minimally describe T-gate's effect on dwell times (actually, the steady-state natural lifetime). Such a simple model would doubtfully predict detailed measurements, e.g., the randomness (49). The dashed region that contains abstract states s₁ and s₂ describes the overall ATP uptake mechanism, which includes T-gate within a Michaelis-Menten structure. The state s₃ represents the remainder of kinesin's chemical cycle. A particular form of the force-dependent rate, k(F) = 1/τ(F), is taken from Eq. 10. Panel b provides a plot of dwell times from the rate model in panel a with parameters deduced by fitting to the model of Nishiyama et al. (33), fitting with better than visual accuracy. That the agreement with Nishiyama et al. is excellent is likely a result of the choice in Eq. 10, but this is not to state that our rate model is identical with theirs (e.g., in the manner [ATP] dependence is included). Used in panel b: δ = 3.10 nm, R₀ = 193, 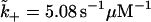, k₋ = 137 s⁻¹, k(0) = 857 s⁻¹, k₃ = 137 s⁻¹, and T = 300 K.

Further development of the waiting mechanism would inappropriately shift emphasis away from the central topics of this article, i.e., the origin of bias and the role of T-gate. No doubt a more detailed rate model could be developed to describe dwell times, but this has been done many times previously.

CONCLUSION

Unlike macroscopic motors at the human scale, microscopic low Reynolds-number environments exclude the possibility of a significant inertial component within a molecular motor. In place of inertial transport, the ability to rectify thermal fluctuations to do work against an external load becomes a simple but powerful principle in cellular processes (3). Power stroke-type models violate this idea with the insistence that configurations change by virtue of a generalized force that exists to overcome fluctuations, which consequently leads to large free energies to sustain a large forward bias. Rectified Brownian motion (RBM) schemes only require that the free energy of ATP is expended to make the boundaries of a process essentially irreversible—diffusional dynamics generate the displacements spontaneously through fluctuations.

Kinesin's biasing mechanism harnesses RBM principles to amplify neck linker zippering by effectively altering boundary conditions, that is, by altering the exponentially sensitive probabilities to visit forward and backward binding sites. At low loads, kinesin's step then is a process that is biased by virtual absorbing and reflecting boundaries (such boundary conditions were taken ad hoc in a previous work (5)), though at high loads and particularly at stall, absorbing and reflecting boundaries are a poor approximation. The remainder of kinesin's stepping is largely orchestrated by T-gate, including the coordination of chemical steps and the appearance of large dwell times at rate-limiting conditions.

Throughout this article, external loads were assumed to be directed toward the traditional microtubule minus-end direction, so as to simulate a cargo. One remaining topic that may assist future efforts is then an understanding of the oppositely-directed forward loading. In particular, large forward loads may be linked to a loss of coordination (by opposing the internal strain that activates T-gate) and strong state unbinding (29), both of which would enhance the rate of kinesin's dissociation from microtubule. Predictions related to this problematic behavior should be attainable within the context of our model.

A larger molecular motor, the actin-based myosin V, could well share an RBM framework in analogy to that found in kinesin. Myosin V is composed of two alternately-stepping heads that are joined together by a pair of semiflexible “legs” (36,37). To draw parallels, the semiflexible legs of myosin should provide the free energy landscape (38), i.e., internal strain, while a small, state-dependent torsional angle should exist in the molecule to cock the system forward and strongly favor forward binding. The large stepping distances of myosin V could then be traversed almost entirely by virtue of thermal fluctuations, while irreversibility is ensured by free energy expenditure related to changes in nucleotide states. Future work will hopefully uncover just how deeply these similarities hold for myosin V and other molecular motors in general.

APPENDIX A: EXTENDED MODEL OF BIASING

This section develops a model to explain kinesin's bias in a manner more complete than the heuristic model. The roles of weak binding, diffusion, and internal strain in these dynamics are incorporated through the considerations discussed in Structural and Chemical Functional Elements. Key results are congruent with those from transition state theory.

The framework of the present model, as with the heuristic model, utilizes a coordinate x along the microtubule that represents the position of an unbound kinesin head relative to the microtubule-bound head. The value x is restricted to exist on the reduced interval x ∈ [−d, d] (see Neck Linkers and the Coiled-Coil Neck), and the boundaries x = ±d of this reduced interval represent binding sites that can induce transitions to and from weak binding states. Connecting the two heads are the neck linkers, which join at a neck linker junction (i.e., an effective coiled-coil) that is located at some point y in the reduced interval. Load is exerted at this junction by the coiled-coil stalk, such that a factor 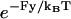weights neck linker contributions in the probability density calculations (see Eq. 11 below).

The combined influence of neck linkers and external load supplies a free energy landscape for the variable x, as partitioned into the stationary Boltzmann distributions p_{z, s}(x) and p_{u, s}(x) for the zippered and unzippered states, respectively. These distributions are obtained through the convolution,

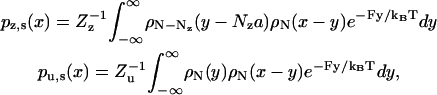(11)

with N the number of peptide units per neck linker, ρ_N the neck linker density (see Eq. 2), F the load force at the junction of the neck linkers, and a the link length. The values Z_z and Z_u are constants at a given load, with their ratio determined by the free energy of zippering Δμ_zu (see Eq. 3):

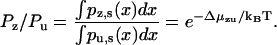(12)

Once Z_z and Z_u are determined by normalization of the total probability P_z + P_u, the stationary probability distribution for the unbound state is known.

For the loads and parameter ranges considered, the distributions in Eqs. 11 and 12 have a single most probable zippering state in the neighborhood of each binding site (zippered for plus-directed binding; unzippered for minus-directed binding). An approximation used routinely below is then to assume that only zippered states bind forward and only unzippered states bind rearward, i.e., to neglect contributions of the less favorable zippering state. Relaxation of this assumption is simple, but clutters the details of the model.

Kinetic aspects of our model are included to determine binding and unbinding rates. This kinetic portion in the reduced interval obeys a pair of coupled, one-dimensional Fokker-Planck equations that reproduce the stationary densities in Eq. 11. Define U_z(x) and U_u(x) to be the respective free energy functions that generate these densities at a given load:

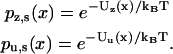(13)

Using these definitions, the nonstationary zippered and unzippered densities p_z(x, t) and p_u(x, t), respectively, are taken to satisfy

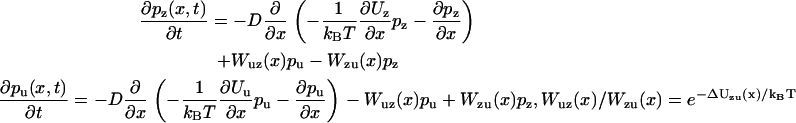(14)

with ΔU_zu(x) = U_z(x) − U_u(x), D the diffusion coefficient, and W_zu(x) and W_uz(x) the transition rates between zippering states. Direct substitution verifies that Eq. 13 is the stationary solution to Eq. 14.

Implicit in Eq. 14 is the peculiarity that the head-to-head separation x is assumed to change on a timescale much slower than the position y of the neck linker junction (y is integrated out). This assumption can be considered merely a modeling simplification, consistent in spirit with the choice to use a reduced interval in place of the coiled-coil (see Neck Linkers and the Coiled-Coil Neck).

Weak binding states in our model may transform to and from diffusing states via weak unbinding and binding, respectively, at the boundaries of the reduced interval (x = ± d). Coupling relations are here given for the plus-end binding site, while behavior for the minus-end site is supposed identical. At a given time, there exists a probability P_W to exist in the weakly bound state. Coupling between the continuously diffusing system and the weak binding state is achieved through the introduction of boundary conditions that linearly relate P_W to the values p_z(x) and 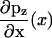at the plus-end boundary (see Appendix B for an alternative, discrete approach). This linear relation is established via two parameters, v₊ and 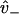, such that

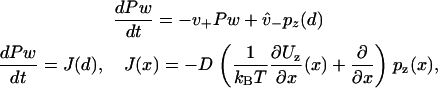(15)

where J(x) is understood to be the probability current in the continuum. Equation 15 implies both 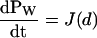, which is the statement of probability conservation, and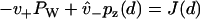, which provides the aforementioned linear boundary condition. The value 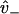is interpreted as the affinity to weakly bind when near a binding site, with binding rate 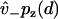. The value v₊ is the rate for a weak state to unbind back into the reduced interval at position x = d. In our model, 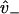is assumed to be a constant, while v₊ may vary with internal strain according to Eq. 4 (thus requiring the calculation of the entropic neck linker force on a weakly bound kinesin head at a given load).

Binding and unbinding rates may now be calculated via approximations similar to those in transition state theory, where, as a simplification, rates most strongly depend on configurations near the binding site (39). The rate formulae below are in this way explored with an uncoupled approach that considers only the single most probable zippering state in the vicinity of each binding site. For conciseness, only the plus-end boundary x = d will be considered. Analogous results apply to the minus-end boundary.

Transition rates between metastable states often reduce to a knowledge of mean first passage times (MFPTs) (39,40), which, for our problem, are the mean times for the system to either weakly bind or unbind. Letting τ(x) be the MFPT for a given process (either binding or unbinding) that at initial time has the position x within the reduced interval, the function τ(x) for a one-dimensional, zippered state head in the potential U_z(x) satisfies (40)

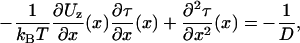(16)

such that a set of boundary conditions (related to weak binding) define a unique solution for τ(x). Equation 16 is solvable with straightforward integrals.

Denote x₀ as some typical point in the reduced interval away from the boundaries (e.g., x₀ = 0), and W as the plus-end weak binding state (not to be confused with the rates W_zu, W_uz). The MFPT for a given process starting at this weak binding state is denoted τ_W. Weak state binding, i.e., the process starting at x₀ and ending at W, is denoted x₀ → W, while unbinding, i.e., the process starting at W and ending at x₀, is denoted W → x₀. The MFPT for each of these may be calculated using Eq. 16 with the boundary conditions

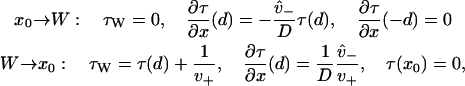(17)

as may be derived from consideration of the backwards equation (40). A brief outline of the derivation that leads to Eq. 17 can be found in Appendix B.

With a few assumptions, related to the free energy profile near the boundary, these MFPTs can be expressed using

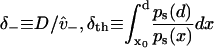(18)

to give

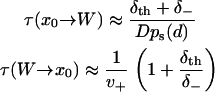(19)

Using Eq. 19, the low affinity (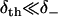) and high affinity (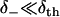) limits are clearly expressed.

The low affinity limit is taken for our modeling, such that δ_th need not be known. On physical grounds, this limit reflects that there exists an entropic barrier before the onset of binding, e.g., due to the orientational specificity of binding that is excluded from the one-dimensional model. As expected from transition state theory, the low affinity limit predicts that the rates of weak binding 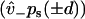and unbinding (v₊) are equal to the quasi-equilibrium rate of crossing the state boundaries x = ± d. In contrast, the high affinity limit problematically hinders escape from the boundaries x = ± d, as indicated by the reduction of the weak state unbinding rate from the desired value v₊.

Once binding and unbinding rates have been determined, calculation of the total bias in our model follows from the rate diagram in Fig. 6, where the rates 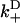, , 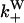and 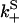are defined in the figure caption. In steady state, the bias (i.e., the ratio of the probability currents J₊ and J₋ for forward and backward binding, respectively) is then

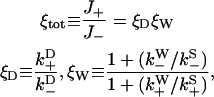(20)

with ξ_D representative of the bias due to diffusion leading to weak binding and ξ_W representative of transitions from weak binding states. As expected, if weak binding states are long-lived compared to strong binding transitions (not generally true), the overall bias is purely a diffusional/zippering effect. Notice that the parameter 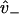disappears from Eq. 20, due to taking the ratio 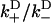(this assumes 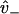is equal at each binding site).

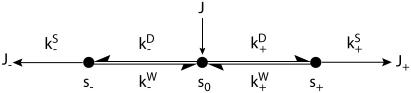
FIGURE 6.

A network diagram to describe the bias of kinesin's step, providing the rates necessary for Eq. 20. The value s₀ represents the reduced interval, the state where one kinesin head remains unbound. The values s₊ and s₋ represent the plus- and minus-end weak binding states, respectively. J is the steady-state probability current entering the process (due to kinesin binding ATP to the microtubule-bound head), and J₊, J₋ are the exiting currents (due to strong binding transitions). The labels 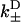are given to the rates of weak binding from a diffusing state, 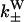to the rates of weak state unbinding (e.g., from Eq. 4), and 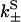to the rates of strong binding. As a simplification, the strong binding rates equal a constant k^S that is independent of load. The essential irreversibility of the strong binding step corresponds to a large free energy decrease for strong binding transitions (consistent with the RBM principle).

Numerical calculation of the stationary distribution p_s(x), needed in Eq. 19, was done with the convolution in Eq. 11. Both Eq. 11 and its normalization can be evaluated through direct numerical integration. For estimates of weak state unbinding (from Eq. 4), the force on a weakly bound head must be known. This may be done by finding the equilibrium position y = y* of the neck linker junction, such that the forces on this junction (due to the load and the forces of the neck linkers) are balanced for kinesin's doubly-bound configuration. The entropic neck linker force in Eq. 1 was in this way used to find y* with a simple root finding routine, which then provided the needed force that determines the rate of weak state unbinding.

APPENDIX B: MEAN FIRST PASSAGE TIME BOUNDARY CONDITIONS

The boundary conditions in Eq. 17, used for the calculation of mean first passage times in Appendix A, are not all obvious at first glance. Their derivation is readily achieved through consideration of a discrete rate theory in the limit of a small grid spacing. Basic steps of this reasoning are presented in the following text, though some well-known results are only cited. A different treatment exists that avoids the limit of a discrete theory. However, such an approach is somewhat less straightforward than the discrete approach.

Consider a series of states labeled with index i. A probabilistic process with one-dimensional, nearest-neighbor transitions is taken to evolve as

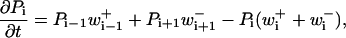(21)

with t the time, P_i the probability to be in state i, and 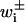the transition rates from state i to states i ± 1. Points of exit for this process may be created through the creation of an absorbing state, such that P_j = 0 is imposed for some state j.

The MFPT problem for Eq. 21 is readily solved. In analogy to the continuous case, the mean first passage time function τ_i is the mean time for a process that starts in state i to first exit via an absorbing state. The function τ_i can be shown to satisfy the recurrence relation (40):

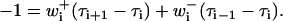(22)

A unique solution to Eq. 22 follows from appropriate boundary conditions, such as τ_j = 0 when there exists an absorbing state at j.

A useful continuous limit exists for a choice of transition rates in Eq. 21. Using the new variable x_i = iδ in the limit δ → 0, the rates

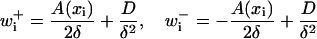(23)

reproduce the distribution of the continuous stochastic process with velocity field A(x) and diffusion constant D (40). Likewise with the above rates, the continuous limit of Eq. 22 is Eq. 16 if .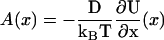

With the above developments, construction of a system with mixed continuous and discrete parts may be analyzed with a discrete approach. For the current demonstration of weak binding and unbinding, a weakly bound state is identified with i = −1, while the continuously diffusing states of an unbound tethered head are identified with i ≥ 0. Transitions to and from the weakly bound state are defined as

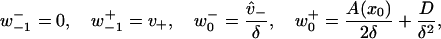(24)

with Eq. 23 defining the remaining transition rates for i > 0. It can be demonstrated that with these definitions, the dynamical boundary conditions of Eq. 15 in Appendix A are satisfied. Thus, the dynamics of this system are as supposed. Additionally, Eq. 22 then straightforwardly leads to both the boundary conditions, Eq. 17, and the continuous equation, Eq. 16, for the MFPT problem, where the cases of weak binding and unbinding in Eq. 17 correspond to the presence or absence, respectively, of an absorbing state at i = −1.