A Kinetic Model Describing the Processivity of Myosin-V

Abstract

The precise details of how myosin-V coordinates the biochemical reactions and mechanical motions of its two head elements to engineer effective processive molecular motion along actin filaments remain unresolved. We compare a quantitative kinetic model of the myosin-V walk, consisting of five basic states augmented by two further states to allow for futile hydrolysis and detachments, with experimental results for run lengths, velocities, and dwell times and their dependence on bulk nucleotide concentrations and external loads in both directions. The model reveals how myosin-V can use the internal strain in the molecule to synchronize the motion of the head elements. Estimates for the rate constants in the reaction cycle and the internal strain energy are obtained by a computational comparison scheme involving an extensive exploration of the large parameter space. This scheme exploits the fact that we have obtained analytic results for our reaction network, e.g., for the velocity but also the run length, diffusion constant, and fraction of backward steps. The agreement with experiment is often reasonable but some open problems are highlighted, in particular the inability of such a general model to reproduce the reported dependence of run length on ADP concentration. The novel way that our approach explores parameter space means that any confirmed discrepancies should give new insights into the reaction network model.

INTRODUCTION

A myosin protein is an ATPase which gains enzymatic activity by attaching to an actin filament (1–3). The myosin proteins use the chemical energy released in ATP-hydrolysis to create directed mechanical motion. More than 100 proteins have been identified as belonging to the myosin superfamily and they are organized into some 18 subgroups (1,4). A myosin is identified by a conserved 80 kDa motor domain and it is usually assumed that all the myosin motor proteins share the same biochemical reaction pathway when hydrolyzing ATP (1). The most studied of the myosins is the nonprocessive (muscle) myosin II whose main reaction path is found to follow the classical Lymn-Taylor scheme (5) describing the correlation of mechanical and chemical events.

Myosin-V is a dimeric protein involved in the intracellular transport of a variety of cargos. The neck region of the two head elements is three times the length of the corresponding region of the myosin II heads (6). It is generally assumed that the long neck region acts as a lever arm and the size of the protein makes it possible for myosin-V to walk hand-over-hand (7–10) following the helical repeat of actin. Myosin-V was the first molecular motor shown to be processive along actin filaments (11). Previously established processive motors like kinesin and dynein use microtubules as the track for their processive directed motion, or in the case of RNA polymerase, DNA. Naturally, there has been much interest both in confirming the processive motion of myosin-V and in gaining insight into the details of the molecule's motion using recent developments in experimental techniques (7–26). Similarly, several theoretical models of the myosin-V walk with different levels of detail have been proposed (12,13,20,22–25,27–31).

How myosin-V coordinates the biochemical reactions and mechanical motions of the two head elements of the protein to become an effective processive molecular motor is an open question. While there is a general agreement on the enzymatic reaction path for a single myosin head, the details of how myosin-V keeps the two heads' reaction cycles in phase is still unresolved. Likewise, there is still a lack of understanding of how external forces directly influence the kinetic mechanism of the walk and what role the internal strain in the molecule plays. As a result of the large number of measurements made on myosin-V in recent years, this is an appropriate time to make more detailed, quantitative models of the myosin-V walk, and to see how such models compare with what is found experimentally.

The outline of the article is as follows: we first establish our model for the processive walk of myosin-V and explain the model's underlying assumptions. In Reaction Rates and Appendix A, we present analytic results for our, rather general, reaction network. These include the velocity, run length, diffusion constant, and fraction of backward steps. These observable quantities are functions that depend on a number of parameters (mainly characteristic energies for the various transitions between states). The unknown parameters are estimated by optimizing the agreement of the model with a chosen representative set of experimental results. This approach, which is based on defining a cost function, is outlined in Optimization. We then present quantitative results for the optimized parameters and compare them with available experimental data and end with a discussion. Agreement with experiment is generally reasonable, though we are unable to explain the trend of the run length with varying ADP concentration. We discuss how our approach might be used to explore such possible discrepancies between existing reaction network models and experiment, generating new insights into the myosin V stepping mechanism.

MODEL

The reaction network for our model is sketched in Fig. 1. The main reaction cycle contains states 1–5. In state 4 the rear head starts its reaction cycle by releasing ADP, while the front head will not react before the whole cycle has been completed making it the new rear head. In state 5 the rear head is in the rigor state with no nucleotide attached, and the rear head will detach rapidly from the actin filament when it reacts with ATP from the bulk. The mechanical motion that moves the rear head into the front position is found experimentally to happen in two steps (22,25), from position 1 to position 2, and then from position 2 to position 3. In state 3 the front head is weakly attached to actin, so only one head is strongly attached in states 1–3, making these the more vulnerable states for total detachment of the molecule from actin. When inorganic phosphate P_i is released from the lead head, going from state 3 to state 4, the myosin binds strongly to actin and the lead head makes the so-called powerstroke. Since the rear head is still attached, the lead head will not achieve the usual post-powerstroke angle with the actin filament, which will cause internal strain in the molecule. This is consistent with electron microscopy (EM) images (9,20) which show strongly bound myosin-V to take a position similar to a telemark-skier's stance, indicating large internal strain in the molecule.

FIGURE 1.

Sketch of the complete reaction network of the model. The Y-shaped molecule is the myosin-V protein which walks on actin filaments. The black actin monomers indicate the attachment sites spaced at ≃36 nm. The labels T, D, and P_i stand for ATP, ADP, and inorganic phosphate, respectively, being bound to the head.

The model given above for the main walk follows fairly closely the intermediate states proposed by Rief et al. (12), which account for the most important experimental findings for myosin-V (13). Note that there is still disagreement in the literature as to which states are present in the main reaction cycle for the processive motion of myosin-V (see for instance (13,22–24,28,30)). A natural consequence of the microscopic size of the motor protein is that both mechanical and chemical effects are important. We expect the external force, due for instance to the viscous drag of a cargo vesicle, to influence most strongly the mechanical steps in the cycle involving translational motion.

The main reaction path is reversible in the sense that one could, in principle, run the ATP hydrolysis reaction in reverse by pulling the motor backward with an external force. (This would not be a very effective way to produce ATP since the motor is kinetically tuned to move efficiently in one direction only.) It is important for a model that aims to investigate the mechanism of a motor protein also to include the effect of futile cycles and detachment rates. Futile cycles consume ATP without creating any net movement of the molecule while detachment limits the run length of the molecule. If, in an evolutionary sense, myosin-V were to tune the reaction rates of the motor domain, it might well seek to maximize the forward velocity (requiring “weak binding”). However, it should probably also seek to minimize the impact of futile cycles and detachment rates (requiring “strong binding”). The kinetic parameters that arise might then be expected to correspond to a suitable compromise solution. We remark that the computational scheme for exploring parameter space that we will later describe could be used in the future to explore such evolutionary pressures and trends.

There will in general be a large number of possible unfavorable pathways, but we will assume that among these there is one dominant futile reaction cycle which takes place when the ADP in state 4 of the main cycle (Fig. 1) detaches from the front head before the rear head moves to state 6. In the futile cycle the front head then reacts with a new ATP molecule so that the molecule returns back to state 2 without having created any net movement. Similarly, we will identify what we believe to be the dominant detachment rate. We make the conjecture that the molecule is most vulnerable to detachment when only one head is attached to actin, as in state 2 (due to the high internal strain in the molecule, state 1 is a short-lived unstable state). We will assume that detachment from state 2 dominates over all other detachment rates. The mechanism of detachment will be the release of ADP followed by the binding of ATP to the rear head so that myosin-V detaches completely from the actin filament before strong attachment is achieved by the front head (state 7, Fig. 1).

The assumption we have made so far is that the main cycle is described well by the qualitative model of Rief et al. (12) where, in addition, the mechanical motion of the rear head to the front is taken in two steps. Furthermore, we assume that there is one futile cycle that dominates over all others, and that this futile cycle involves states 2 and 4 in the main cycle. Lastly, we assume that the detachment rate at state 2 dominates all others. The complete model we have outlined (shown in Figs. 1 and 2) is a minimal realistic model for the walk of a molecular motor like myosin-V.

FIGURE 2.

The main and futile cycles combined in one scheme showing all the reaction paths between the seven states in the complete model. See also Fig. 1. The reaction rates are given by the corresponding equations in the text. Reaction steps which release and bind ADP, P_i, or ATP are indicated.

REACTION RATES

The reaction rates between the different states are described by Arrhenius expressions,

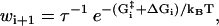(1)

where τ is the fundamental timescale of the reaction and k_B is the Boltzmann constant. (We use the notation where u_i and w_i are the forward and backward rates, respectively, away from state i (32).) The value 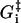is the energy barrier between state i and its neighbor state in the forward direction, while ΔG_i is the energy difference between the two states. We set T = 298 K in this article. The total energy balance for the ATP hydrolysis is

(2)

where the nucleotide concentrations are made dimensionless by dividing by the concentrations at the reference states for ΔG_i, [ATP]⁰ = [ADP]⁰ = [P_i]⁰ = 1 M. The standard free energy is given by 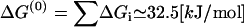(33), which is close to 13 k_BT, while ΔG_hyd ≃ 25 k_BT at cellular conditions (2).

For the main cycle, one ends up with a total of 10 reaction rates. The first four rate constants in the main cycle are related to the mechanical movement (see Figs. 1 and 3),

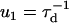(3)

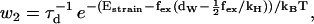(4)

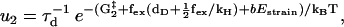(5)

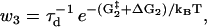(6)

where τ_d is a hydrodynamic timescale related to diffusion over one step-length and f_ex is the component of the external force parallel to the actin filament. The mechanical step is separated into a so-called working stroke of d_W ≃ 25 nm and a diffusional substep of d_D ≃ 11 nm (see Fig. 3), as indicated by experimental findings (22,25), giving a total step size d = d_W + d_D ≃ 36 nm (11,12,18). Thus we neglect the (weak) external force dependence of the diffusional step size in u₁ but capture the dominant effect of the force in, e.g., retarding the activated rate u₂ and in distorting the metastable shape of the bound arm in state 2 (through the ∼ terms in the exponents of w₂ and u₂). The total internal strain in the molecule E_strain defines an effective Hookeian spring constant, k_H, related to the compliance in the motor and neck region of the myosin head,

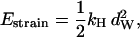(7)

where we have assumed that the molecule is fully strained in state 1.

FIGURE 3.

The mechanical movement of myosin-V takes place in two separate steps. The first step, through a distance d_W ≃ 25 nm, is from the highly strained state 1 to state 2 where the internal strain balances the external force. When the molecule diffuses to state 3, through a further distance d_D ≃ 11 nm, the internal strain increases to bE_strain.

State 2 is in mechanical equilibrium. The position of the hinge/neck in state 2 is influenced by the magnitude of the external force, which gives rise to the energy term 1/2 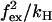in w₂ and u₂ (Eqs. 4 and 5). When moving from state 2, either back to state 1 or forward to state 3, the molecule increases its internal strain by E_strain or 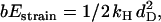respectively (Fig. 3). Using the latter expression together with Eq. 7 gives b = (d_D/d_W)² ≃ 0.2. Since E_strain > bE_strain, there is a bias in the forward direction away from state 2, making the molecule a Brownian ratchet (34).

Notice that the external force f_ex is defined to be positive in the direction opposite to the movement of the myosin-V molecule, and that only the influence of the force parallel to the actin filament is taken into account. (The external force is of course a vector quantity, with a possible important influence on the walk arising from the normal component of the force (35,36).) The external force will accelerate or slow down the two reaction rates w₂ and u₂ away from state 2, depending on the sign of f_ex.

Experimentally, it is found that there is one rate-limiting step in the walk of myosin-V (14–16). At large external force, f_ex, one or more substeps that couple to the force, will become rate-limiting. A phenomenological way to model this is (11)

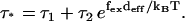(8)

Here τ_* is the (average) dwell time for one step, while τ₁ and τ₂ are the dwell times of the force independent and dependent substeps, respectively, and the external force couples to a distance d_eff. When fitting experimental data to this phenomenological equation, naively one would expect d_eff ≃ 36 nm, which is the average step length. Instead it was found that d_eff is between 10–15 nm. From our model this scale emerges quite naturally, since the external force couples to the diffusional search governed by rate u₂, which gives τ ≃ τ₁ + 1/u₂. From Eq. 5 we have

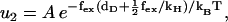(9)

where A is some constant. Here d_D is 11 nm, while the correction term of the position of the hinge in state 2 is of the order of 8 nm when close to stall force. It is satisfying that this is consistent with the value of d_eff cited above and indicates that the way we include the two substeps in our model is reasonable. (See (27) for a discussion of the limitations of Eq. 8.)

The reaction rates for states with both heads attached to actin (see Fig. 1) are given by

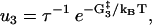(10)

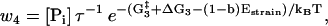(11)

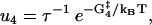(12)

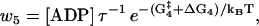(13)

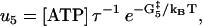(14)

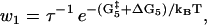(15)

where the nucleotide concentrations and [P_i] in Eqs. 11, 13 and 14 are given as dimensionless quantities (see comments under Eq. 2). The value τ is a microscopic timescale related to the characteristic oscillation frequency of the protein. The free parameters in the model are the activation energies 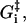the energy differences ΔG_i, and the strain energies. When an estimate is made for these free parameters, the resulting energy landscape (Fig. 4) gives directly all the predicted reaction rates, and the model's predictions for myosin-V's velocity and run lengths along the actin filament (see Appendix A). Note that τ is not really an independent variable since it can be absorbed into the activation energies: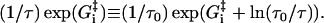

FIGURE 4.

The one-dimensional energy landscape that we find for the walk of myosin-V in which the states in the model are indicated by the solid circles. Energy is measured in units of k_BT. The energy changes associated with the dashed transitions are E_strain and bE_strain, being the energy barriers involved in moving away from state 2. Also shown is the rate-limiting activation energy 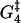between state 4 and state 5. The generalized reaction coordinate X can be thought of as measuring the progress around the main reaction cycle (Fig. 1). As such, it reflects a combination of physical motion and the progress of biochemical reactions, according to the substep. The shape of the curve is somewhat arbitrary, but the peaks and the troughs are at the correct energies determined by the optimal values ( and ΔG_i) where the energies are recalculated for the reference concentrations [ATP] = 1 nM, [ADP] = [P_i] = 0.1 μM, i.e., the log of each concentration appears in the energy barriers.

As a measurement of the deviation away from equilibrium one can introduce the parameter

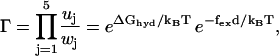(16)

which gives the thermodynamic driving force for the molecular motor (32,37). To fulfill detailed balance we have Γ = 1 at equilibrium (37). As expected from the energy balance the external force appears in Γ as f_exd; this is the total work done by the motor when completing one reaction cycle with step-length d. From Eq. 16 it is clear how the external force shifts the apparent equilibrium constant of the hydrolysis reaction. This coupling between the external force and the free energy of the hydrolysis of ATP, gives directly the thermodynamic upper bound on the stall force f_stall = ΔG_hyd/d (≃2.8 pN at cellular conditions). The presence of futile cycles will influence the upper bound on the stall force, but this correction is found to be insignificant for our (best) model.

The reaction rates for the futile cycle are given by

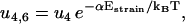(17)

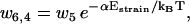(18)

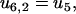(19)

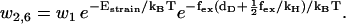(20)

Here u_{i, j} and w_{i, j} are the reaction rates from state i to state j. Using the fact that the two head elements are structurally identical, we make the assumption that the front head has to have the neck at a similar angle to that between the rear neck and the actin filament in step 4 of the main cycle to make it possible for ADP to be released or bind to the myosin motor domain (Eqs. 17 and 18). To achieve this, the front head has to overcome the strain energy in the molecule in state 4 which creates an energy barrier αE_strain for the ADP release reaction governed by rate u_4,6 (see Fig. 3). In this way myosin-V synchronizes the biochemical reactions of the two heads.

To move from state 2 to state 6 (Fig. 1), the molecule has to increase the internal strain by E_strain without the energy from the hydrolysis reaction (Eq. 20), so there is a very low probability for the futile cycle to run in reverse (effectively becoming a useful reaction pathway). The reaction rates in the futile cycle follow the reaction rates for the main cycle except for the extra barrier caused by the strain in the molecule, so there is only one new parameter that appears in the model. In principle, αE_strain could be estimated if the elastic moduli of the different parts of the molecule were known, by making a detailed structural model based on EM measurements (20) and crystal structures (38,39) of myosin-V (see also (30)). We will not attempt to do this here, but leave αE_strain as an undetermined energy barrier, an energy barrier used by myosin-V to synchronize the reaction cycles of the two head elements.

The detachment from state 2 takes place if the ADP detaches from the rear head before the front head becomes weakly bound. The relevant reaction rates are

(21)

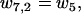(22)

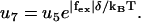(23)

The external force will increase the detachment rate of the single head (an effect we neglect when both heads are strongly attached, which should be a good approximation when considering the strain level in the molecule). Pulling experiments on S1 give an apparent interaction distance of δ = 2.4 nm (21) for the external force (Eq. 23).

An extended model where we would also consider the reattachment rate of motors is of course possible (40), but not particularly relevant since the local bulk concentration of motors and of actin target sites is usually not well-controlled in an experiment. Our main focus in this model will be single-molecule experiments and their predictions.

In our model we use the fact that the two head regions of the myosin-V protein are identical and have identical biochemical reaction paths. It might seem at first that this would be an obstacle to the processive motion of the protein, since the reactions of the two heads must be out of phase to ensure that at all times at least one of the two heads is strongly attached to the actin filament. However, evidence has been found in EM experiments that the intramolecular strain affects the two bound heads asymmetrically (9,20). The model outlined above shows explicitly how this asymmetrical strain can be used by the two heads to coordinate their reaction cycles and to minimize the impact of the futile cycles and detachment rates.

PARAMETERS

The fundamental timescales, τ and τ_d can be estimated using the Stokes-Einstein relation. The value τ_d is related to the diffusion time of the whole head element (with a diameter of ≃30 nm) over the step size d_W ≃ 25 nm, which gives τ_d ≃ 10⁻⁵ s. Similarly, τ is related to movement of a few nanometers, where the relevant length scale is the thickness of the head element, giving τ ≃ 10⁻⁸ s. Note that any difference between τ or τ_d in the different steps will be absorbed into the activation energies 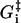(see comment under Eq. 15) so we are only interested in the order of magnitude of these timescales. Similarly, the activation energies will also be modified by the bulk pH and ionic strength, even though the influence of these solution properties are not included explicitly in the model.

Estimates of some of the activation energies are available through chemical kinetic reaction rate measurements, but we will not try to guess the values of the activation energies but leave them all as free parameters. The model of the myosin-V walk outlined above is a fairly detailed model containing seven different states and 13 reaction rates, but the number of undetermined parameters is still relatively low. We have the four activation energies, 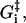three independent energy differences ΔG_i (where one energy difference will be dependent because of Eq. 2), and finally two terms connected to the strain level in the molecule, E_strain and αE_strain. We are therefore left with nine undetermined parameters in our model of the myosin-V walk, which is a small number considering that the model is able to predict not only the walk's dependence on the bulk concentrations of ATP, ADP, and P_i, but also how the external force couples to the walk. The model is also detailed in its prediction of how the internal strain influences the walk and the level of strain in the molecule. Our model is therefore overdetermined with respect to the available experimental data and provides many measurable predictions.

OPTIMIZATION

To search the parameter space computationally we define a cost function which quantifies the agreement between the model and the data. There is clearly some subjectivity involved in choosing the terms in the cost function: for example, one might be more inclined to include data that have been confirmed by several different research groups. We cannot investigate all possible permutations of our cost function since the optimization approach is quite computationally demanding. However, the 17 experimental features that we identify, and encode in the cost function, are those that we expect a good model for the walk of myosin-V to reproduce. These include trends observed under variation of nucleotide bulk concentrations and the external force. Each term in the cost function was included to search for such a trend or to restrict the value of the energy jumps ΔG_i between substeps. Likewise, we specify variances to indicate how large a deviation from each target value we deem acceptable. The cost function, Δ, given in Appendix B, is constructed as a simple sum of 17 terms and each term gives an O(1) contribution when within the accepted experimental error (as defined by our chosen variance). We believe that our cost function is a minimal encoding of the most important experimental trends, but it is possible to extend or modify our approach by including further or different data points if desired.

We do not choose arbitrarily what values the nine undetermined parameters should take but instead search the parameter space for favorable combinations using a technique based on simulated annealing (41) of the cost function. To make the search effective, we first evaluate the cost function at 50,000,000 points in a parameter space of (25 k_BT)⁹. (This is the energy available in the hydrolysis reaction, Eq. 2, under cellular conditions. The internal energy E_strain and energy differences ΔG_i cannot be larger than the energy in the hydrolysis reaction, while there are no such limits in principle on the kinetic parameters and αE_strain.) To make sure these points are evenly spread in the parameter space we use the Sobol quasi-random sequence (41,42). The 50 points with the lowest cost function from the Sobol sampling were then passed to a simulated annealing routine, where the cost function is the energy term. The number of steps in the simulated annealing is chosen so that it is equal to the number of steps in a random walk over the average distance between the Sobol points.

An attractive feature of estimating the free parameters in the model like this is that it has some similarities to the way the molecular motor has tuned the same parameters through evolution to achieve physiologically required velocities and run lengths under variable cellular conditions.

RESULTS

After optimizing the parameters for our model (Table 1), it was found that there is one rate-limiting step, u₄ = 14.7 s⁻¹, corresponding to the largest value of for i = 2, …, 5, which is the release of ADP from the rear head in state 4, Fig. 1. The ADP release rate is in quantitative agreement with kinetic measurements (11,13–16,22,24), which estimates u₄ between 10 s⁻¹ and 20 s⁻¹. From the model (Fig. 1) it can be seen why ADP release is the crucial reaction step for the myosin-V walk, since both the futile cycle and detachment depend on it. By slowing down the ADP release, myosin-V achieves a larger duty ratio for the myosin head, but more importantly, also reduces the flux around the futile cycle and similarly the detachment rate. Since the rate-limiting step also determines the average velocity of the motor, there is a tradeoff when tuning the rate of u₄. It is satisfying that the optimization scheme of our model is able to reproduce the kinetic tuning found experimentally. It is worth noting that no optimal solutions were found in other parts of the parameter space, i.e., no other possible combination of reaction rates could be found with either a different rate-limiting step or more than one rate-limiting step.

TABLE 1.

The estimated values (in units of k_BT) of the free parameters in the model as given by the optimization routine (see also Fig. 4)

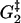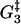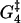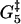				Estrain	αEstrain	ΔG2	ΔG3	ΔG4	ΔG5
0.3	10.4	15.7	5.8	12.8	5.4	0.14	9.9	−10	13.1

The optimized best-fit model parameters, as given in Table 1, give rise to u₅ = 0.3 μM s⁻¹ for the attachment rate of ATP to the rear head in state 5, a prediction that is somewhat slower than experimental estimates of u₅ in the range from 0.6 to 1.5 μM s⁻¹ (22). The release of P_i is found to be fast when the front head is attached weakly to actin (state 3, Fig. 1) with u₃ = 3200 s⁻¹, an order-of-magnitude above the lower bound from kinetic measurements u₃ > 250 s⁻¹ (14).

It is a somewhat subtle point that the velocities and run lengths that our model predicts (see Appendix A) are independent of one aspect of that model, specifically whether the mechanical motion between state 3 and state 4 is assumed to happen before or during the release of P_i. This is despite the fact that the forms of Eqs. 10 and 11 are sensitive to this difference: the (1 – b)E_strain term would appear in the exponential in u₃ and not in w₄ if the mechanical transition occurred before the phosphate release rather than during the phosphate release, as we assume here. The reason for this is that the optimization process fixes only the observable rates (u₃ and w₄). This appears to suggest that there may be some ambiguity in the value of the energy that appears in these rates, depending on whether the motion between state 3 and state 4 happens before or during the release of P_i, i.e., whether the peak in the energy landscape occurs closer to state 4 or state 3, respectively. We can nonetheless determine the form of the equations by considering the kinetic measurements for P_i release. These are carried out using single myosin heads without internal strain. If, for the intact two-headed molecule, the (1 – b)E_strain term was instead placed in the exponential in u₃ (and the peak in the energy landscape was close to state 4), then the rate for a strain-free transition, such as would be expected to be the case for single-headed molecules, would be larger by a factor of exp [(1 – b)E_strain], giving rise to unrealistic phosphate release rates that would be four orders-of-magnitude higher than 3200 s⁻¹. This provides quantitative evidence that the power stroke of the front lever arm takes place substantially after P_i is released, as is illustrated in Fig. 4 where the energy barrier between state 3 and state 4 is close to state 3.

We estimate the internal strain, E_strain = 12.8 k_BT, which gives a rigidity κ = 120 k_BT nm = 500 pN nm² for the lever arm (43), in agreement with other estimates in the literature (44). This gives a Young modulus of Y = 0.6 GPa, assuming the myosin neck has an effective radius of 1 nm, which is comparable to what is found in similar proteins (2). The strain barrier, αE_strain, preventing the futile cycle, was found in the optimization scheme to be 5.4 k_BT, which slows down the release of ADP from the front head (state 4, Fig. 1) ∼50–200 times compared to the rear head under changing nucleotide concentrations in the bulk. This is consistent with measurements reported by Rosenfeld and Sweeney (24).

Among the more important properties of myosin-V are its velocity and processivity along the actin filament. We are interested in how these two properties are influenced by the bulk concentrations of nucleotides and the presence of an external force in our model. In single-molecule experiments, all of these parameters can be controlled and monitored, giving rise to direct measurements of their influence on the myosin-V walk.

The velocity of myosin-V has been measured at between 200 and 500 nm/s (13), which is consistent with the magnitude of the velocities predicted by the model. The velocity appears to follow a Michaelis-Menten-like form in which it becomes independent of ATP at high ATP concentration, while linearly dependent on ATP at low ATP concentrations (Fig. 5). There is similarly found to be a strong dependence of the velocity on the ADP concentration. P_i only has a measurable influence on the velocity (and the run length) at very large excess concentrations, similarly to what is found experimentally (13,23). When comparing the velocity dependence on concentration of ATP and ADP directly with experimental measurements (23), we find reasonable quantitative agreement (Fig. 5).

FIGURE 5.

Predictions of velocity of myosin-V as a function of ADP, ATP, and P_i concentration that arise from our optimized (best) model with parameter values as shown in Table 1 (and used in all subsequent figures). In each case the other two reference concentrations are taken from [ATP] = 1 mM, [ADP] = 0.1 μM, or [P_i] = 0.1 μM. The experimental data for varying [ATP] (squares) and [ADP] (circles) are from Baker et al. (23).

Our model reproduces the trend of velocity with increasing external force (see Fig. 6), as found experimentally in Uemura et al. (25). Note that our model only considers the external force parallel to the motion of myosin-V along actin, while in an experiment optical loads are usually applied both along the axis of movement and perpendicular to it (35,36). This might explain some of the discrepancies observed at large external forces. When applying a negative external force (pulling in the forward direction), the velocity is not found to increase significantly as has also been found by Clemen et al. (26). When the pulling force in the direction of the motion exceeds 2 pN, we find that the average velocity decreases, since the molecule tends, increasingly, to be pulled off the actin track thereby populating state 7 in the reaction cycle (Fig. 1) and reducing the forward motion. This reduction in the average velocity at large negative force was not observed by Clemen et al. (26).

FIGURE 6.

The velocity as a function of force. The solid line (and circles) show results when [ATP] = 1 mM and [ADP] = 200 μM, the dashed line (and squares) when [ATP] = 1 mM and [ADP] = 1 μM, while for the dotted line (and diamonds) we have [ATP] = 10 μM and [ADP] = 1 μM. The model (the lines) shows similar trends to what is found experimentally (the circles, squares, and diamonds) (25).

Related to the velocity of myosin-V is the dwell time, t_d, defined by Eq. 49 in Appendix A, which is the average time it takes before the molecule takes a forward step (11,27). Comparing the prediction of the model for the dependence of dwell time on force with experimental results (11,25) reveals fair agreement for high ADP and high ATP concentration and the correct trend, although poor quantitative agreement, for high ATP but low ADP concentration (Fig. 7). However, the model is not able to reproduce the finding (11,25) that the dwell time becomes independent of force at low ATP concentration.

FIGURE 7.

Dwell time for [ATP] = 2 mM (solid line/circles), [ATP] = 10 μM (dotted line/squares), and [ATP] = 1 mM and [ADP] = 200 μM (dashed line/triangles). The experimental data are from Mehta et al. (11) (circles) and Uemura et al. (25) (squares and triangles).

An important parameter for a processive motor is the duty ratio (2), r_d, the average proportion of the time the head is strongly attached to actin. The duty ratio of myosin-V is found to be close to 90% (24), while our model predicts even higher duty ratio at low forces (Fig. 8). As expected, the duty ratio is reduced at higher external force, since the mechanical motion from state 1 to state 3 is slowed down, and becomes rate-limiting at ∼1.6 pN at saturating ATP concentrations, which is consistent with experimental results of 1.5 pN (11,13).

FIGURE 8.

The duty ratio, r_d, as a function of force for [ATP] = 1 mM, [ADP] = [P_i] = 0.1 μM.

Baker et al. (23) have measured run lengths of myosin-V as a function of ADP and ATP concentrations. When looking at the dependence of the run length on the ATP concentration, our model predicts a decrease in run length when increasing the ATP concentration (Fig. 9), which is consistent with experimental results (23). The run length is found from our model by finding the eigenvalue of the matrix of rate constants which gives the slowest relaxation time in the system (see Appendix A). Since there is one dominating eigenvalue, we get a single exponential decay in run length.

FIGURE 9.

Run length L for different concentrations of ATP when the ADP concentration is equal to 1 mM (dotted-dashed line), 100 μM (dashed line), and 10 μM (solid line). At low ADP concentration, the run length becomes independent of ATP concentration. The prediction of the model is compared with experimental results at low ADP concentrations (circles) (23).

We find a nonmonotonic dependency of the run length on the ADP concentration, as is also found experimentally. (The nonmonotonicity leads to the crossing over of the [ADP] = 1 mM and [ADP] = 1 μM lines on Fig. 9 at low ATP concentrations.) However, while Baker et al. (23) find a strong increase in the run length when decreasing the ADP concentration below [ADP] = 1 mM, our model predicts a decrease in the run length (Fig. 9). It is not immediately obvious why our model does not reproduce this experimental finding. It is clear that the model neglects many possible futile cycles and detachment rates and maybe even other possible useful reaction cycles. For instance, in Baker et al. (23), it is suggested that myosin-V needs two useful reaction cycles to be able to function under variable conditions. Even though our model only has one main reaction cycle it seems to be able to reproduce many of the experimental findings under very different conditions, casting some doubt on this earlier assertion. It does not seem at all obvious that it would be of physiological advantage for myosin-V to reduce its run length under increase of the ADP concentration. This may suggest that futile cycles not included in our model play a role. Finally, this puzzle indicates that the ADP dependence of the run length is worthy of further experimental investigation.

The run length drops off exponentially when increasing the force, as shown in Fig. 10. The run length is also found to be strongly influenced by pulling in the forward direction (negative force). This can be understood by considering Fig. 8. The duty ratio increases with a negative external force since the mechanical movement from state 1 to state 3 is accelerated. This also makes it less likely that the molecule will end up in state 7 and detach (Fig. 1). At high negative external forces though, the run length is decreased, since the larger force is pulling the molecule off the actin track (Eq. 23). This nonmonotonic behavior in the run length as a function of force was not observed in a recent study (26), which found the run length of myosin-V to be fairly insensitive to both positive and negative external force over a large range of values. Note that our model probably exaggerates the increase in attachment rate of the front head to actin when pulled strongly in the forward direction. For a strong force, the position of state 2 (Fig. 3) might change so much that the front head no longer is in the target zone, slowing down the diffusion to the target site. If a correction for this had been included in our model we believe that the run length increase for a negative external force would be reduced.

FIGURE 10.

Run length L for different strengths of the external force when [ATP] = 1 mM and [ADP] = 200 μM. For negative external force, the run length has a nonmonotonic behavior, where it increases 10-fold before decreasing again.

Using Eq. 48, Fig. 11 shows the fraction of backward steps is found to be low until ∼2 pN, consistent with experimental findings (12,26). As is shown in Fig. 11, the model predicts that the fraction of backward steps is larger at low ATP concentrations, again in agreement with experimental results (11,13).

FIGURE 11.

The fraction of backward steps, π₋, is insignificant in the model until an external force of ∼2 pN is reached. The solid line is for [ATP] = 2 mM and [ADP] = 200 μM, while the dashed line is for a reduced ATP concentration of 100 μM.

A quantitative measure of the stochastic deviations from uniform constant-speed motion (Fig. 12) is given by the so-called randomness ratio (27,45), ρ = 2D/Vd, where D is the dispersion given by Eq. 50. The reciprocal of ρ gives a measure of the number of rate-limiting steps, and for different ATP concentrations and external forces, it is found that the model gives only one rate-limiting step. This is somewhat different from earlier theoretical predictions (27), and experimental measurements of the randomness ratio can be used to differentiate between theoretical models. At high forces, ρ diverges because of the vanishing velocity close to stall force.

FIGURE 12.

The randomness ratio, ρ, as a function of force at different ATP concentrations.

A biochemical reaction network is expected to be robust to small changes in the kinetic parameters (46). This robustness is needed to tackle both the natural changes that occur inside a cell during its lifetime and the fact that cellular biochemical reaction networks are highly interconnected, so a perturbation in one affects many others. A simple and effective robustness test is to see how the motion of the motors is affected by changes of ±5% in the different parameters. This also gives information on which parameters have the largest influence on, for instance, the velocity and run length of the molecule in the model. Fig. 13 shows that 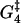and to a lesser degree E_strain have the largest influence on the run length, while ΔG₄ is the only parameter that gives significant changes in the velocity when perturbed. The importance of 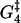and ΔG₄ in controlling velocity and run length is to be expected, since these are the parameters determining the rate constants u₄ and w₄ for ADP release from and recapture by the rear head between states 4 and 5, which we have found to be the rate-limiting step.

FIGURE 13.

The circle shows the unperturbed velocity and run length for [ATP] = 1 mM, [ADP] = [P_i] = 0.1 μM, and zero external force. The squares show the influence on run length and velocity of changes of ±5% in each of the nine free parameters of the model (while keeping the other parameters fixed). The run length is very sensitive to changes in 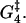Also perturbing in E_strain gives quite a large change in run length. Large variation in velocity was only observed when perturbing the parameter ΔG₄.

Since the temperature enters explicitly in our equations, via the thermal energy scale k_BT, it is natural to look at how the temperature influences the run length and the velocity. Some caution should be noted though, since some of the free energy terms themselves are known to be directly dependent on temperature (24). Fig. 14 is obtained under the assumption that none of the energy terms depend strongly on temperature.

FIGURE 14.

Temperature dependence of velocity and run length (when [ATP] = 1 mM and [ADP] = 200 μM). The model predicts an increase in velocity with temperature, but a decrease of the run length. The velocity is found to be more sensitive to changes in temperature than the run length.

DISCUSSION

Many reasonable and well-justified models of the myosin-V walk exist in the literature, but the majority of the models are of a qualitative nature and often introduce unnecessary (and uncontrolled) approximations when employed to obtain quantitative predictions. Of quantitative models in the spirit of this work, one interesting early study for myosin-V is due to Kolomeisky and Fisher (27), who considered a two-state model that took some account of step-size variations. It was found that there is a substep in the walk of myosin-V creating another possible reaction pathway, as also suggested in some experiments (25,47). One shortcoming in our model is that the model does not allow for the possibility that the geometry or mechanics of the walk can change in different regimes, as, for instance, at very different bulk concentrations or external forces. It is still an open question whether motor proteins change behavior in a dramatic way in different regimes, but some evidence suggests that stepping length is influenced by force (22,25,26). Some recent articles (30,31) have tried to calculate explicitly the different strain energies for the different step lengths, which would be helpful to clarify the detailed mechanism of the motion of myosin-V. One problem in such calculations is that several angles and rigidities are not well known so that the number of free parameters becomes very large.

There is necessarily some arbitrariness as to how many and which distinct states are included in a model, since the concept is strictly only a useful approximation to the complex, fluctuating motion of the protein. Several substates (and thereby substeps in the main reaction cycle), which have been identified experimentally or on thermodynamic grounds (16,39,48), are not included in this model. This means that the subreaction rates between some of the states have been combined into one effective rate. Where possible, we have chosen not to excessively coarse-grain the state space, e.g., by classifying many states together into fewer, more broadly defined states. Philosophically this seems wise if one is not certain a priori that such coarse-graining of state space will not reduce the precision or predictive power of the model. We also feel that it is of value that the model takes into account all the steps where the protein reacts with smaller bulk molecules, since bulk concentration is something that can be controlled experimentally. Similarly, we wanted to separate out the different steps that are expected to couple to the external force. As a result, the proposed model can make direct predictions as to how the external force produced by an optical tweezer, for instance, should change the behavior of the myosin-V walk. In any case, it is important to remember that the complexity of a model such as ours is not really a function of the number of states but rather the number of parameters, which remains small, the interpretation of the parameters, which remains physically clear, and the reaction network topology.

The elastic strain in the molecule plays several roles in our model; most importantly, the strain in the molecule synchronizes the chemical reactions of the two myosin heads. This is vital for making myosin-V an effective processive motor (22). The synchronization is caused by the slowing down of the ADP release from the lead head compared to the rear head in state 4, since the internal strain makes it less likely for the lead head to have the optimal angle relative to the actin filament necessary for ADP release. A related benefit of this is that the slowing down of ADP release from the lead head minimizes the impact of the futile cycle. Also, the strain biases the detached head to stay in the target zone (state 2, Figs. 1 and 2) when doing the (11-nm) biased diffusional search for the next attachment site on the actin filament. This bias both increases the velocity of the motor, since less time is used in the diffusional search for the next target site on the actin, and increases the processivity by decreasing the time spent with only one head strongly attached to the actin.

The model does not contain any direct dissipation of free energy ΔG_diss. Such dissipation by friction and heat loss caused by the nonequilibrium motion of the protein would reduce the total useful work that the molecular motor could do by reducing the effective free energy of the hydrolysis reaction ΔG_eff = ΔG_hyd – ΔG_diss. We have not tried to quantify the size of ΔG_diss but assumed that it is relatively small. It would of course be possible to include ΔG_diss as an undetermined parameter, even though we have chosen not to do this here. The model does take into account the energy dissipated by the futile hydrolysis of ATP by the futile cycle (Fig. 1) that does no work and creates no net movement, but since αE_strain is estimated to be relatively large, the release rate of ADP from the front head in state 4 (Fig. 1) is reduced two orders-of-magnitude compared to the release of the rear head. This indicates that myosin-V is a tightly coupled motor under all conditions and the futile cycle will not dissipate significant energy.

The starting point for our model was the qualitative model proposed by Rief et al. (12) and the observation that myosin-V has a so-called powerstroke movement and a diffusional search. There are several alternative mechanisms suggested in the literature, although they typically have a lot in common since there is general agreement on the single head reaction mechanism. One influential alternative model has been proposed by De La Cruz et al. (49) where the strong attachment of the front head to actin is triggered by the release of the rear head. It is also possible to envision there being several parallel reaction paths followed by the motor, where all these paths contribute significantly to the forward motion. It would be natural to assume that different paths dominate in different regimes, which would then provide a strategy for the motor to function well under varying conditions. One interesting example (23) of such a parallel reaction path mechanism involved combining the models of Rief et al. and De La Cruz et al. into a version with two paths. Taking into account the number of proposed models in the literature and then the possibility of different combinations of the various models, the number of permutations of possible models is clearly very large. We argue that a more quantitative analysis of the competing models would often be useful, e.g., using a computational scheme similar to that presented here.

We have presented a moderately detailed model of the walk of myosin-V, and compared the accuracy of the model with experimental measurements for velocities, run lengths, and dwell times at different nucleotide concentrations and external forces. Predictions are also made for as yet unmeasured quantities, such as the internal strain in the molecule and the randomness ratio. The model also clearly shows how the internal strain can be used by myosin-V to coordinate its forward motion. A clear advantage of our model is that the physical significance of parameters in the model is transparent. This transparency makes the model a useful reference for comparison to future experiments and aids in the identification of elements of the model which are accurate and elements that need refinement. As our work and other recent quantitative studies have demonstrated, it is possible to give a clear analysis of very detailed models. Even when experimental data are individually not conclusive, the large number of existing experimental measurements available should help to differentiate the models when they are analyzed in such detail. In turn this will be useful in clarifying the underlying mechanism of the myosin-V walk, which is still not precisely understood.

We remark that ours is the first attempt to explore carefully whether a full reaction cycle, with a nearly complete list of relevant parameters, is or is not able to reproduce the trends observed over a variety of experimental studies. There are several useful outcomes from our study. With the exception of the dependence of run length on ADP concentration our model does appear to be broadly consistent with the experimental observations. We are still unable to explain even the qualitative nature of the run-length dependence on ADP concentration. This is a puzzle, which might signify a flaw in the accepted models and which we flag for future experimental attention. In addition, we find that phosphate release must be coupled to a release of energy over much of the transition between states 3 and 4 if the model is to produce results that are consistent with known rates of P_i release.

APPENDIX A: ANALYTICAL EXPRESSIONS

These expressions were used to compare with experimental data.

The master equations for the probabilities, P_j, of finding the molecule in state j, can be deduced from Fig. 2 to be

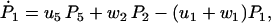(24)

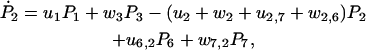(25)

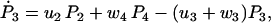(26)

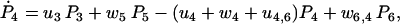(27)

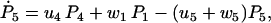(28)

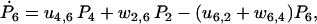(29)

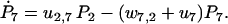(30)

In matrix notation we have

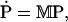(31)

where M is the 7 × 7 reaction rate matrix and the j^th component of the vector P is P_j.

The probability of finding the molecule in one of states 1–7 is not conserved under Eq. 31 since the motor drops off the actin track at a rate u₇ from state 7 (Eq. 30). To solve Eq. 31, it is helpful to renormalize, eliminating dropoff, to get a probability-conserving equation. This is done by writing

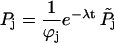(32)

and choosing the constants φ_j such that the renormalized probabilities satisfy a conservative set of equations. It is possible to show that this can be done (see (50)) if

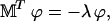(33)

and that then the vector of renormalized probabilities satisfies the equation

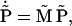(34)

where 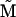is a renormalized reaction-rate matrix with 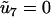and renormalized rate constants

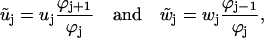(35)

for j = 1…5, where the index is periodic with period 5, and

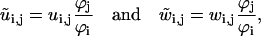(36)

for the rate constants not on the main reaction cycle.

The slowest, dominant eigenvalue, −λ₀, is negative for reasonable rate constants, while the faster eigenvalues can be complex giving rise to fast oscillations in the reaction network.

At long times, tends to the steady-state solution of Eq. 34 (50), found by solving 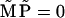analytically. The relaxation times of oscillations are found to be fast compared to the stepping time and to 1/λ₀, so it is clear from Eq. 32 that the solution for P_j at long times will be dominated by the slowest eigenvalue, −λ₀. We therefore choose ϕ to be the corresponding eigenvector of the transposed matrix Since there are seven states in our model, this eigenvalue problem is best solved numerically.

In the following equations we assume all the rate constants are renormalized and drop the tilde. We look for steady-state solutions 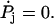(For another approach to achieve analytical expressions for a fairly similar reaction network, see (51)). The net flux between two neighboring states is given by J = P_ju_j – P_j+1w_j+1, and we seek to express the steady-state probabilities P_j in terms of the futile flux J_fut = P₆u_{6, 2} – P₂w_{2, 6} and the main reaction flux J_hyd = V/d = P₁u₁ – P₂w₂. It can be shown that the steady-state solution is given by

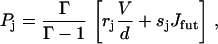(37)

for j = 1, …, 5, P₇ = (u_2,7/w_7,2)P₂, and

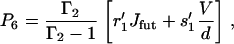(38)

where Γ is given by Eq. 16 and

(39)

Here we have introduced the auxiliary functions

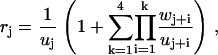(40)

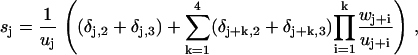(41)

for j = 1, …, 5, where δ_{j, i} is the Kronecker delta function (with δ_{j, i} ≡ δ_{j+5, i}) and where the indices on the rate constants are periodic with period 5. We have similar auxiliary functions relating to the futile cycle, namely

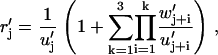(42)

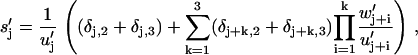(43)

for j = 1, …, 4, where w′_j = w_j and u′_j = u_j except for w′₁ = w_6,4, w′₂ = w_2,6, u′₁ = u_6,2, and u′₄ = u_4,6. We now have a period of four, u′_j ≡ u′_j+4, w′_j ≡ w′_j+4, and δ_j,i ≡ δ_j+4,i, since there are four states that participate in the futile cycle (Fig. 1).

Using the conservation of probability 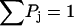(since dropoff has been eliminated through renormalization) and a second independent expression for P₄,

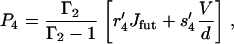(44)

one can derive the analytical expressions for the velocity, V, and the futile flux, J_fut,

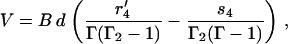(45)

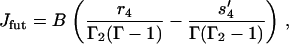(46)

where

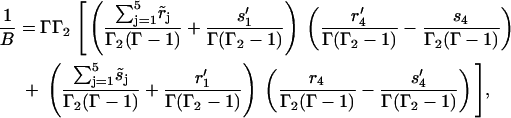(47)

with 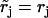and 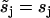for j = 1, 3, 4, 5, while and

With the probability of finding the molecule in each state now determined, we can use previously established analytical expressions. The fraction of backward steps is (27,52)

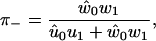(48)

where 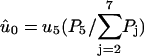and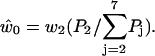

The mean forward-step dwell time is given by (27,52)

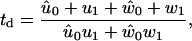(49)

and the dispersion is given by (32,53)

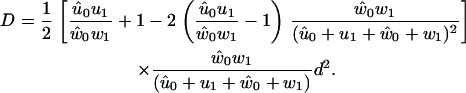(50)

Since the probability of the myosin remaining attached to the actin filament decays exponentially with the dominant eigenvalue −λ₀, the typical duration of a run is 1/λ₀ and hence the run length L is given by

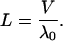(51)

APPENDIX B: COST FUNCTION

The cost function contains 17 terms. Except where other concentrations are explicitly mentioned, the nucleotide concentrations are given by [ATP] = 1 mM and [ADP] = [P_i] = 0.1 μM. Likewise, the external force is assumed to be zero, except if stated otherwise.

The first term in the cost function is constructed from the model velocity, V, compared to the velocity V^E estimated from experimental data in the literature (11,12,14,15,23,25). The mean-squared uncertainty in the measured velocities, 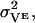are, in general, found to be ∼10%:

(52)

When the ADP concentration increases, the velocity V^E is found to decrease (12,14,15,19,23). We choose a second and third ADP concentration, [ADP]⁽²⁾ = 200 μM and [ADP]⁽³⁾ = 2.5 mM, and construct additional terms in the cost function at these conditions:

(53)

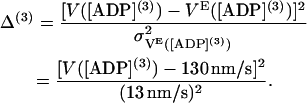(54)

When the ATP concentration decreases, the velocity V^E is found to decrease (8,23). Choosing [ATP]⁽²⁾ = 10 μM, we construct a fourth term,

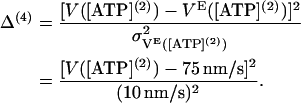(55)

It is found that changing [P_i] several millimolar does not significantly change the velocity of myosin-V (13,23). Choosing [P_i]⁽²⁾ = 40 mM, we add a fifth term using measurements by Baker et al. (23)

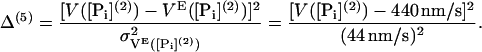(56)

Baker et al. (23) have performed a large number of experiments on the run length L at different nucleotide concentrations finding that the run length is increased with a decrease in the concentration of either ADP or ATP. We introduce four terms to the cost function based on run lengths at different nucleotide concentrations (where [ATP]⁽³⁾ = 100 μM):

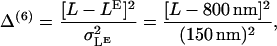(57)

(58)

(59)

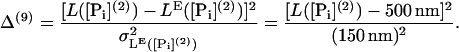(60)

The velocity is found to be independent of external force up to (12,13,15) and we include a 10th term based on this,

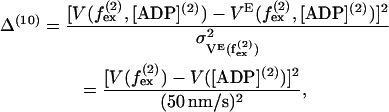(61)

where V([ADP]⁽²⁾) is the velocity in Eq. 53. Similarly, it was found that run length is fairly independent of external force (26), giving the 11th term

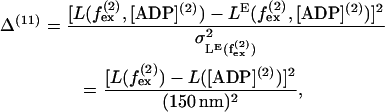(62)

where L([ADP]⁽²⁾) = 400 nm (23). Also dwell time is found to be independent of external force up to (11,25) giving rise to the 12th term,

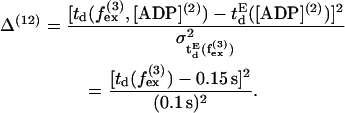(63)

Rosenfeld and Sweeney (24) found that the release of ADP from the front head is at least 50 times slower than from the rear head, which gives rise to the 13th term,

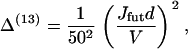(64)

where J_fut is the futile flux (Eq. 46). The last four terms are restrictions on the possible values of the energy jumps ΔG_i, reflecting some inherent limits caused by strict limits on the energy available in each substep of the chemical reaction. Using measurements on S1 (see Table 2) as rough target values, but allowing for a deviation from these values of 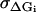= 3 k_BT the last four terms are

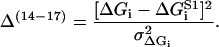(65)

TABLE 2.

Energy jumps (in k_BT units) measured for the reaction of S1 with actin (taken from Table 14.2 from (2) using Eq. 2)

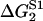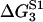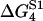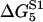2	5.7	−7.7	15.3

The total cost function is simply defined to be the sum of all the different cost terms,

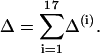(66)

All the terms in the cost function cannot be expected to constrain completely independent properties of the model. However, with 17 differing constraints on only nine free parameters it is encouraging, and perhaps not surprising, that the optimization reveals that the best solutions are grouped in the same region of parameter space.