Heteropolymer Collapse Theory for Protein Folding in the Pressure-Temperature Plane

Abstract

We revisit a heteropolymer collapse theory originally introduced to explore how the balance between hydrophobic interactions and configurational entropy determines the thermal stability of globular proteins at ambient pressure. We generalize the theory by introducing a basic statistical mechanical treatment for how pressure impacts the solvent-mediated interactions between hydrophobic amino-acid residues. In particular, we estimate the strength of the hydrophobic interactions using a molecular thermodynamic model for the interfacial free energy between liquid water and a curved hydrophobic solute. The model, which also reproduces many of the distinctive thermodynamic properties of aqueous solutions in bulk and interfacial environments, predicts that the water-solute interfacial free energy is significantly reduced by the application of high hydrostatic pressures. This allows water to penetrate into folded heteropolymers at high pressure and break apart their hydrophobic cores, a scenario suggested earlier by information theory calculations. As a result, folded heteropolymers are predicted to display the kind of closed region of stability in the pressure-temperature plane exhibited by native proteins. We compare predictions of the collapse theory with experimental data for several proteins.

INTRODUCTION

Native proteins in aqueous solution are generally only marginally stable with respect to denaturation and tend to unfold to form biologically inactive states if the thermodynamic conditions of the solution are significantly perturbed. On one hand, this sensitivity to changes in environmental variables presents a practical barrier to maintaining activity during analysis, purification, storage, or delivery of protein solutions. On the other hand, much in general can be learned about the physics of protein folding/unfolding by experimentally applying various types of stresses to protein solutions and then measuring the corresponding responses. For instance, analysis of experimental data on the thermodynamics of protein unfolding reveals that its distinctive temperature dependence is similar to that of transferring a nonpolar solute from its own neat phase into water (1). This evidence, along with the fact that nonpolar solvents denature proteins, led Kauzmann to surmise nearly half a century ago that the ability of native proteins to bury their nonpolar amino-acid residues in a core, away from water, was central to their thermal stability (2,3). Although other types of forces are also involved in protein folding (e.g., hydrogen-bonding, London-van der Waals interactions, and electrostatics), it is now widely accepted that Kauzmann's hypothesis about the central role of hydrophobic interactions in determining the thermal stability of the native state was largely correct (4). In fact, hydrophobic interactions are known to also be an important driving force in a broad class of association phenomena in aqueous solutions, including membrane and micelle self-assembly, ligand-protein binding, protein-protein complexing, and protein aggregation (4–8).

The aforementioned connection between hydrophobic interactions and protein stability can be tested more stringently by constructing theoretical models that make falsifiable predictions about the thermodynamic and structural changes that accompany protein folding. One such strategy begins by viewing proteins as heteropolymers consisting of coarse-grained segments with interactions that reflect the aqueous-phase solubilities of the corresponding amino acids of the protein sequence (9,10). This type of approach has two main advantages. First, it leads to models that are based on independently testable principles of polymer physics and hydration thermodynamics. Second, the behavior of these models can often be determined by analytical theories and elementary numerical techniques. Of course, the quantitative predictions of such models ultimately depend on the details of the presumed interactions and the approximations used in obtaining the solution. However, their general success as tools for understanding the thermal stability of proteins derives from the fact that heteropolymers can display behavior, similar to proteins, resulting from a competition between two driving forces: the tendency of the molecule to collapse into a compact state to reduce the nonpolar surface area in contact with aqueous solution versus the drive to unfold from this compact state to realize more configurational degrees of freedom. This balance can give rise to classic two-state (native versus denatured) behavior with an intervening free energy barrier, which is in agreement with the experimental trends exhibited by many small globular proteins (11).

Here, we revisit a physically insightful heteropolymer collapse (HPC) theory developed by Dill and collaborators that qualitatively predicts the basic thermodynamic trends for protein stability at ambient pressure (9,12). Our main focus is to address a limitation of the theory: it cannot make predictions about the factors that affect the pressure stability of proteins. One reason for this is that HPC theory does not provide a prescription to account for the effect of pressure on the solvent-mediated hydrophobic interactions that drive protein folding. Specifically, it assumes that the contact free energy between hydrophobic amino-acid residues is directly proportional to the free energy χ(T)k_BT associated with physically transferring a hydrophobic amino-acid residue from its own pure phase into water. Dill and collaborators determine χ(T) from a thermodynamic parameterization of oil-water partitioning data for hydrophobic amino-acid side chains at ambient pressure (9). However, an analogous parameterization for the pressure-dependent oil-water partitioning of amino acids is not available for use in the theory. Even if it were, directly employing it in HPC theory with no other modifications would lead to qualitatively incorrect predictions because, as Kauzmann pointed out in 1987, the sign of the volume change associated with the transfer of nonpolar molecules into water is inconsistent with the pressure denaturation of proteins (13). The implication is that 1), hydrophobic forces are not a dominant factor in determining the pressure stability of proteins and/or 2), the hydrocarbon transfer model fails to capture the effect of pressure on hydrophobic interactions.

The former appears consistent with the most widely accepted view of pressure denaturation in the experimental literature, which might be summarized as follows. Compressibilities and direct effects of pressure on interactions are found to play secondary roles, while the main driving force for pressure denaturation is simply the differences in specific volume between the native and denatured states that exist at ambient pressure; the denatured state becomes more stable with increasing pressure because it exhibits a smaller specific volume (see, e.g., (14–16)). The differences in specific volume are due to cavities and void spaces that are solvated upon unfolding (17–21), electrostriction of charged or polar groups (18), and the hydration of hydrophobic residues exposed to solvent upon unfolding. Both the sign and the magnitude of the volume change associated with exposure of hydrophobic residues to water have been debated (see, e.g., (14,18,22)). However, recent pressure perturbation calorimetry measurements (23–25) indicate that, for temperatures between ∼0°C and 30°C and moderate pressures, hydration of polar amino-acid side chains results in a decrease in specific volume, while hydration of hydrophobic amino-acid residues results in an increase in specific volume.

Nonetheless, detailed molecular simulations (26,27) and information theory calculations (28,29) indicate that these experimental observations may not reflect a comprehensive picture of the effect of pressure on the thermodynamics and interactions of hydrophobic residues. In particular, pressure may in fact significantly destabilize the hydrophobic interactions between nonpolar species in water, in contrast to what would be expected based on the hydrocarbon transfer model. The results from these simulation studies have led to the notion that weakening of hydrophobic interactions allows water to penetrate into the hydrophobic interior of native proteins, ultimately denaturing them by breaking their core structure apart. Of course, simulation results such as these are only as reliable as the models that they use for the relevant intermolecular interactions. However, the models employed in the above studies are known to reproduce other well-known experimental signatures of hydrophobic effects (26,27,29), and we are not aware of any experimental studies that contradict their qualitative volumetric properties.

Motivated by the above observations, we generalize the HPC theory in this study to provide a simple test for whether pressure-induced changes to hydrophobic interactions can significantly destabilize the native state. In this first step, we do not try to incorporate all of the known contributions to pressure denaturation (cavities in the native state, electrostriction, etc.) into the HPC theory. Rather, we simply propose a new strategy wherein interactions between nonpolar amino acids and water in HPC theory are estimated using a molecular thermodynamic model that predicts the temperature- and pressure-dependent interfacial free energy between a curved hydrophobic solute and water.

The main advantage of this new strategy is that the model used to calculate the strength of the hydrophobic interactions satisfies some stringent conditions for reproducing water's peculiar thermodynamic behavior (in particular, how pressure and temperature affect its properties (30–32)). As expected, the model predicts that χ exhibits a maximum in temperature, and thus heteropolymers exhibit both cold and warm denaturation. Interestingly, χ also displays a maximum in pressure, which leads to both pressure- and tension-induced unfolding. As a result, the revised HPC theory qualitatively predicts the closed regions of native-state stability in the pressure-temperature plane that are observed for globular proteins (33). It also captures some basic experimental trends for how point mutations modify native-state stability.

The outline of the article is as follows. First, we provide a brief explanation of the HPC theory of Dill and co-workers and introduce our generalization to treat the hydrophobic interactions from a molecular thermodynamic model. Then, we examine the temperature and pressure predictions of the modified HPC theory, comparing the model results to experimental data. Finally, we present some concluding remarks about the theory.

HPC THEORY REVISITED

Here we briefly review the HPC theory developed by Dill and collaborators, and we discuss the main physics involved with the temperature-dependent collapse transition. We also outline our approach for generalizing the theory to study the effect of hydrostatic pressure on folding.

Background

Since the mathematical details of HPC theory are discussed in previous publications (see, in particular, (9) and (12)), we focus exclusively on the inputs, outputs, and the essential physics of the approach here. Basically, proteins are modeled as coarse-grained polymers with sequences of polar and nonpolar segments. Depending on the number of residues N_r, the fraction of those residues considered hydrophobic Φ (e.g., based on an aqueous-phase solubility criterion (9,34)), and the strength of the hydrophobic interactions χ(T), they adopt either a collapsed native state or an expanded denatured state.

Heteropolymer collapse at infinite dilution is modeled as an equilibrium process driven by formation of favorable hydrophobic-hydrophobic residue contacts and opposed by loss of chain conformational entropy. In calculating the free energy of folding ΔG_f, the effective attractive strength between the hydrophobic residues in solution is assumed to scale with χ(T)k_BT, a quantity that can be viewed as the free energy required to transfer a nonpolar segment from the hydrophobic protein core to the solvent-accessible protein surface. The Bragg-Williams mean-field approximation (35) is used to determine the number of nonpolar intraprotein segment contacts, and the Flory approximation (36) is used to account for how the number of chain conformations depends on segment density. Finally, the random copolymer approximation is invoked so that N_r, and not the actual order of the amino acids in the protein sequence, is treated explicitly.

In the most commonly applied manifestation of the theory (9), χ(T) is chosen to capture the qualitative trends for the experimental transfer of hydrophobic amino acids from a nonpolar liquid phase into water (34,37), and it is modeled using the following form:

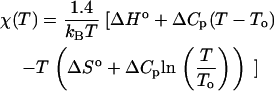(1)

Here, T is temperature; k_B is Boltzmann's constant; ΔH^o and ΔS^o are the enthalpy and entropy of transfer at T = T_o, respectively; and ΔC_p is the heat capacity of transfer. The factor 1.4 accounts for the number of residues per polymer segment (12). If T_o = 298 K, then setting ΔH^o = 0, ΔS^o = −6.7 cal K⁻¹mol⁻¹, and ΔC_p = 55 cal K⁻¹ mol⁻¹ leads to reasonable agreement with experimental transfer data (37). The temperature-dependence of χ(T) displays a maximum that corresponds to the characteristic solubility minimum of hydrophobic compounds in water (see, e.g., (1,4,9)).

This particular version of HPC theory is simple, but it still reproduces, and thus provides a physical basis for understanding, many experimental trends for protein behavior at ambient pressure. For example, it predicts the distinctive entropic and enthalpic contributions to the thermodynamics of protein unfolding, and it identifies how the thermal signatures of hydrophobic hydration can lead to cold denaturation (9). The model also provides thermodynamic and coarse structural information about the individual native and denatured states, such as their radii of gyration and the number of hydrophobic residues on their solvent-exposed surfaces. This information can be used to derive effective protein-protein interactions in solution (38), which in turn provides an avenue for studying equilibrium unfolding curves and global phase diagrams for protein solutions via molecular simulation (39).

HPC theory also captures the fact that modifications to sequence composition (e.g., N_r and Φ) and solution conditions (e.g., T and pH) affect the structure of the expanded and collapsed states (10). For example, polymer chains with sequences of higher Φ exhibit more compact denatured structures because water is a poor solvent for their apolar residues. This latter result is in accord with basic principles from polymer physics and experimental observations of proteins (40). In addition, increasing temperature results in more expanded denatured states, owing to the weaker hydrophobic interactions and relatively larger contribution of configurational entropy to the free energy of folding.

However, as mentioned in the Introduction, while this version of HPC theory qualitatively predicts the temperature-dependence of protein stability, it cannot make predictions about the pressure-induced denaturation of proteins. To accomplish this, one needs to modify χ to account for the effects of pressure.

PRESSURE-DEPENDENCE OF HYDROPHOBIC INTERACTIONS

The volume change associated with protein unfolding is negative at high pressures, whereas the volume change accompanying the transfer of a hydrocarbon from a nonpolar phase into water is typically positive under the same conditions. Thus, the hydrocarbon transfer model for protein unfolding, which was successfully exploited by HPC theory to study the thermal stability of proteins at ambient pressure (9), is not sufficient on its own to capture pressure effects (13). As a result, it is not possible to successfully extend HPC theory by simply parameterizing χ(T, P) to describe solute partitioning experiments at elevated pressures.

However, both information theory calculations (28,29) and detailed molecular simulations (26,27) provide strong evidence that increasing pressure, at constant temperature, weakens the effective attractions between hydrophobic species in aqueous solution. In fact, it has been proposed that this weakening allows water molecules to penetrate into the hydrophobic channels of the protein core, denaturing the protein at high pressures by dissociating internal residue contacts (28). Stated differently, the application of high hydrostatic pressures reduces the thermodynamic penalty for creating new solvent-accessible surface area in the hydrophobic core of the protein. Motivated by this simple physical interpretation, we extend HPC theory here by allowing χ to reflect how pressure modifies the excess free energy associated with creating interfacial contact area between hydrophobic residues and liquid water.

In particular, we determine χ(T, P) by assuming that the following equality holds that

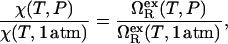(2)

where 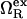is the excess grand potential (relative to bulk) which quantifies the free energy associated with forming an interface between liquid water and a hydrophobic surface of curvature R⁻¹. In the context of HPC theory, R⁻¹ can be viewed as representing the mean curvature of the solvent-accessible hydrophobic patches that liquid water contacts as it penetrates into the core structure of the protein during pressure denaturation. In the small curvature limit (σ_wR⁻¹ ≪ 1, where σ_w represents the effective diameter of a water molecule), 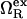is proportional to the macroscopic interfacial tension between liquid water and a planar hydrophobic surface (41,42). On the other hand, molecular-scale hydrophobic effects (29,43,44) dominate 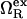for solvent-accessible interfaces with high local curvature (σ_wR⁻¹ ≈ 1). Of course, one expects the hydration geometries in actual proteins to be heterogeneous, involving curvatures intermediate between the aforementioned molecular and macroscopic limits (7,8,42,45,46). As we discuss below, 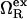shows quantitatively different pressure dependencies for solutes with small and large curvatures, allowing us to test the R⁻¹-dependent predictions of our modified HPC theory against experimental results for the pressure denaturation of proteins. This comparison provides one way to calibrate R⁻¹ for our theory and to gain some basic insights into which types of hydration processes are consistent with the experimental data for pressure unfolding.

In our model for χ(T, P) given by Eq. 2, we calculate 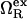via the expression

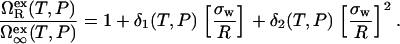(3)

Here, 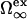is the excess grand potential associated with forming a planar interface between liquid water and a smooth hard wall. We compute this quantity using an analytical molecular thermodynamic theory for water developed by Truskett and co-workers (30–32). This theory was chosen because it satisfies some stringent conditions for reproducing the thermodynamics of water and aqueous mixtures, including their global fluid phase behaviors, distinctive thermal anomalies (e.g., volume, isothermal compressibility and isobaric heat capacity minima), and the hydration of both small hydrophobic solutes and macroscopic hydrophobic surfaces. The state-dependent coefficients δ₁(T, P) and δ₂(T, P) in Eq. 3 determine the first- and second-order corrections for curvature, respectively. We obtain these via an optimized scaled particle formalism introduced by Henderson (47), which allows us to maintain internal self-consistency with the molecular thermodynamic theory (30,32) that we employ to calculate 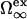and water's equation of state. To ensure recovery of the earlier HPC theory of Dill and co-workers at ambient pressure (9), we equate χ(T, 1 atm) in Eq. 2 to χ(T) of Eq. 1.

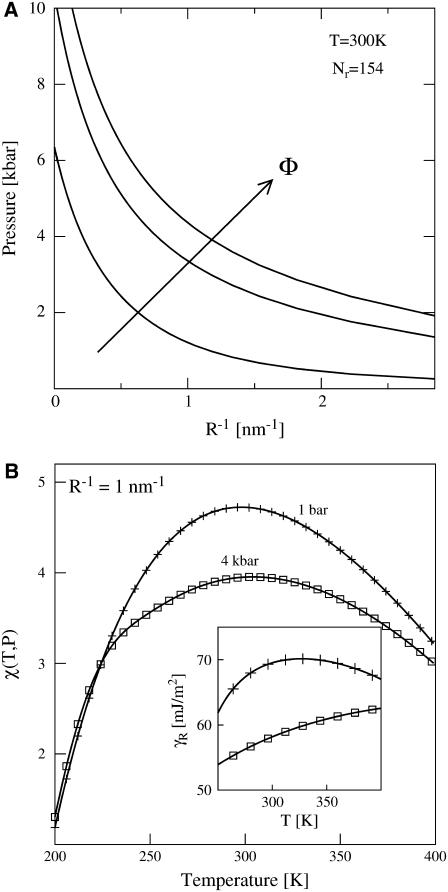
In Fig. 1 a, we use HPC theory together with our modified model for χ to calculate how sequence-hydrophobicity Φ and mean-hydration curvature R⁻¹ generically affect the midpoint pressure P_m of the T = 300 K unfolding transition, i.e., where ΔG_f(300K, P_m) = 0. We do not invoke the simplifying factorization approximation that Dill and collaborators use in obtaining Eq. A26 from Eq. A25 of Dill et al. (9), but this only results in small quantitative differences with their ambient pressure results. We examine the behaviors of three model heteropolymers with N_r = 154 and Φ = 0.4, 0.5, and 0.6, sequence parameters typical of those found in medium-sized, single-domain globular proteins (48). The values of curvature shown in Fig. 1 a span from macroscopic to molecular lengthscales 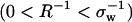. Interestingly, these heteropolymers are predicted to exhibit pressure-induced unfolding transitions in the range 0 kbar < P_m < 10 kbar, with the precise unfolding pressure for any individual polymer being determined from its specific combination of sequence-hydrophobicity Φ and hydration-curvature R⁻¹.

FIGURE 1.

(a) Midpoint-folding pressure P_m versus mean hydrophobic hydration-curvature R⁻¹ for model proteins of chain length N_r = 154, Φ = 0.4, 0.5, and 0.6 at T = 300 K using the modified HPC theory. The arrow indicates increasing sequence hydrophobicity. (b) Plot of the modified χ(T, P) dependence on temperature at P = 1 bar (plus symbols) and P = 4 kbar (squares) for R⁻¹ = 1 nm⁻¹. The inset shows the dependence of the effective interfacial surface tension γ_R with temperature at P = 1 bar (plus symbols) and P = 4 kbar (squares).

Clearly, hydration-curvature R⁻¹ impacts the quantitative, but not the qualitative, results for pressure denaturation. As is shown in Fig. 1 a, if macroscopic interfacial thermodynamics prevails (i.e., R⁻¹ ≈ 0), then unfolding occurs in the approximate range 6 kbar < P_m < 10 kbar. On the other hand, assuming molecular-scale hydration physics (i.e., 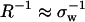) leads to pressure-induced unfolding transitions in the range of 0 kbar < P_m < 2 kbar. Since the HPC model does not treat fine structural details, additional experimental information is required to assign a specific value for R⁻¹ to a given protein system. For instance, one might select a value of R⁻¹ so that the theory closely matches P_m for a particular protein of interest. Alternatively, one might use geometric information regarding hydration structure obtained from experiments or simulations to estimate R⁻¹. Here, we simply note that many biomolecules, including globular proteins, lose stability experimentally in the pressure range 1 kbar < P_m < 5 kbar (33,49). Fig. 1 a shows that the revised HPC model reproduces this range of experimental unfolding pressures if one chooses R⁻¹ to be on the order of 1 nm⁻¹, a lengthscale intermediate between the macroscopic and the molecular limits. Based on this simple analysis, we assign R⁻¹ = 1 nm⁻¹ for the rest of the calculations in this study, and we focus on probing how the other physical parameters in the theory affect the pressure-dependent thermodynamics of the collapse transition.

Fig. 1 b shows how χ varies with temperature both at ambient pressure (P = 1 atm) and at a much higher pressure (P = 4 kbar) where denaturation readily occurs for many proteins. The ambient pressure result coincides, by construction, with Dill and collaborators' original parameterization of χ(T) given by Eq. 1. It exhibits a maximum with temperature, a thermal signature of the hydrophobic effect associated with the experimentally observed solubility minimum of small nonpolar molecules in water (1). Because of this feature, significant heating (or cooling) weakens the hydrophobic attractions that stabilize the folded state and thus provides a driving force for loss of stability by warm (or cold) denaturation.

The temperature-dependence of χ at 4 kbar is qualitatively similar to that observed at 1 atm. However, as with water's other thermodynamic anomalies (32), the maximum becomes less pronounced at high pressure because the resulting density is higher than at 1 atm and thus less compatible (50) with the open hydrogen-bond network that water exhibits under ambient conditions. The elevated pressure of 4 kbar also reduces the overall strength of the hydrophobic attractions (relative to those at ambient pressure) by ∼1 k_BT in the temperature range 275 K < T < 325 K. The inset of Fig. 1 b illustrates that this can be viewed as a consequence of pressure reducing the effective interfacial tension, defined as 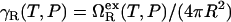, between water and the hydrophobic patches in the protein core by ∼10 mJ/m² in the same temperature range. This reduction in γ_R results in the denaturation of marginally stable heteropolymers because it allows water to penetrate into and break apart their hydrophobic cores.

Although its implications for the pressure denaturation of proteins have not been previously considered, the fact that elevated pressures can reduce the effective interfacial tension between a dense liquid and a solvophobic surface has been appreciated for some time (see, e.g., (47,51)). The physical reason for this effect is easy to understand. At ambient pressure, the effective interfacial tension between an attractive liquid and a solvophobic surface is large in magnitude and positive because of the considerable enthalpic penalty associated with forming the interface. However, application of high hydrostatic pressure (e.g., several kbars) appreciably increases the solvent density, forcing the solvent molecules to primarily sample the steeply repulsive (i.e., hard-sphere) portion of their intermolecular pair potential. Thus, increasing pressure progressively causes the attractive solvent to behave more like a hard-sphere fluid near a hard surface. Since the effective interfacial tension between a hard-sphere solvent and a hard surface is negative due to the entropic depletion effect (47), the application of large pressures will thus generally result in a significant decrease in the effective interfacial tension between an attractive liquid and a solvophobic surface.

Finally, we note that the effective interfacial tension between a solvent and a solvophobic surface can also be decreased appreciably by putting the solvent under large tensions (i.e., negative pressures) (see, e.g., (46)). This behavior occurs because negative pressures significantly reduce the density of the solvent, which, in turn, reduces the enthalpic penalty of forming a solvent-surface interface.

As a result of the two limiting behaviors discussed above, the effective interfacial tension exhibits a maximum as a function of pressure (or density). This maximum is expected to be a fairly general phenomenon, and it has been observed in simulations of the attractive square-well fluid near solvophobic wall (47,51). In the context of heteropolymer stability, it provides a driving force for unfolding at either high hydrostatic pressures or large tensions. We return to this point in the next section when exploring the global stability of heteropolymers in the pressure-temperature plane.

PROTEIN STABILITY IN THE P-T PLANE: PREDICTIONS AND EXPERIMENTS

In this section, we use HPC theory together with our molecular thermodynamic model for χ(T, P) to make some general predictions about native-state stability of single-domain globular proteins in the pressure-temperature plane. We also explore how well the theory can reproduce some specific experimental trends for both ribonuclease A (RNase) and staphylococcal nuclease (SNase) in their wild-type and mutated forms.

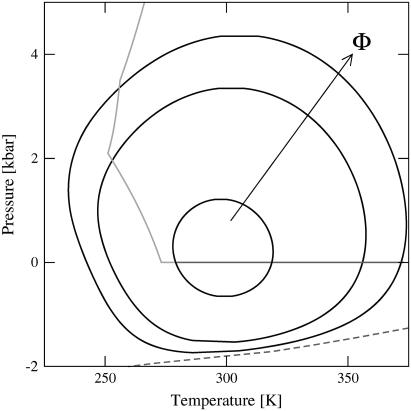
To begin, we plot in Fig. 2 the predicted loci of midpoint folding transitions (i.e., the collection of T, P coordinate pairs that satisfy ΔG_f(T,P) = 0) for three model heteropolymers with R⁻¹ = 1 nm⁻¹ and sequence parameters equivalent to those of Fig. 1 a. The folded states for these polymers show closed regions of stability in the P-T plane. In other words, unfolding can occur by isobaric heating or cooling, or by the isothermal application of pressure or tension (i.e., negative pressure). This type of closed-loop stability behavior is consistent with the available experimental data for a number of proteins (52–56) and with the results of computer simulation studies of model proteins where explicit solvent is included (see, e.g., (50,57)). Although the thermodynamics of hydrophobic hydration both for supercooled water and for water under tension have been studied via simulation (46,58), to our knowledge, the possibility of unfolding proteins in the latter type of solution has yet to be probed by either simulations or experiments (although negative effective pressures obtained via solvent perturbation have been explored (59)).

FIGURE 2.

Loci of midpoint-folding transitions for the model proteins N_r = 154, Φ = 0.4, 0.5, and 0.6 calculated from modified HPC theory. The arrow shows increasing sequence hydrophobicity. The enclosed regions indicate the predicted pressures and temperatures that favor the compact, native state. The solid shaded lines represent the freezing and boiling transitions for water that bound the thermodynamically stable conditions for the liquid state. The dashed line represents water's spinodal curve predicted from the molecular thermodynamic model for water (30,32) used in determining χ(T, P).

The notion that native proteins should generally exhibit a closed region of stability in the P-T plane was arrived at earlier through the predictions of a phenomenological thermodynamic theory originally introduced by Hawley (52) and recently reviewed in a broader context by Smeller (33). This thermodynamic approach, similar to the present HPC theory, assumes that folding can be described by an equilibrium two-state model. It involves expanding ΔG_f to second-order in P and T, which allows one to relate the midpoint folding transition (where ΔG_f(T, P) = 0) to folding-induced changes in isothermal compressibility, thermal expansivity, and heat capacity. For proteins, it predicts an elliptical stability diagram very similar in shape to those of Fig. 2 derived from our modified HPC theory. One can view HPC theory as providing a complementary microscopic perspective to the phenomenological theory of Hawley because the former derives stability directly from the physics of folding, i.e., from the temperature- and pressure-dependent competition between intraprotein hydrophobic interactions χ(T, P) (which favor the folded state) and protein configurational entropy (which favors the unfolded state).

In Fig. 2, we also show water's freezing and boiling transitions, which together provide bounds to the thermodynamic conditions that favor the liquid state. Cooling at ambient pressure eventually leads to freezing. Therefore, to observe cold denaturation experimentally, careful consideration must be made to prevent crystal nucleation and maintain the protein solution in its liquid phase. However, at higher pressures (e.g., 2 kbar), the liquid phase of water is stable for an expanded temperature range. Due to the shapes of the loci of midpoint transitions for the polymers shown in Fig. 2, cold denaturation is predicted to be readily observable in the stable liquid. This prediction is consistent with experimental studies that utilize high pressure to study the cold denaturation of proteins in solution (52–54,60). As discussed earlier, the revised HPC theory presented here also predicts that proteins will unfold in liquid water at negative pressures (i.e., in the stretched liquid). Fig. 2 shows that this transition is predicted to occur before reaching the spinodal, the absolute limit on stretching where cavitation spontaneously occurs. Thus, it should be possible to induce the unfolding of marginally stable proteins by applying tension (61) to the protein solution.

Another key result of Fig. 2 is that increasing the hydrophobic content of the heteropolymers in HPC theory from Φ = 0.4 to Φ = 0.6 leads to significantly increased temperature and pressure stability. This makes good physical sense given that hydrophobic interactions in the interior core of proteins preferentially stabilize their folded states. The present level of theory also predicts that heteropolymers of the same Φ, but different monomer sequences, exhibit the same thermodynamic stability. This, of course, is an artifact of the level of random copolymer approximation applied in the HPC theory. It will be interesting to address this type of issue in future work by applying a more rigorous theoretical treatment (e.g., (62)) that accounts for detailed sequence-dependent interactions.

The Φ-dependent stability predictions displayed in Fig. 2 are in good qualitative agreement with the experimental results for the single-domain globular proteins RNase and SNase provided in Table 1. We choose these proteins for comparison because 1), they both approximately exhibit a two-state folding transition; and 2), the point mutation data allows us to readily study the main effects of changes to sequence hydrophobicity on stability. The point mutations for both RNase and SNase occur in sequence locations that contain either a chain-folding initiation site (63,64) or are in the hydrophobic core (65). Chain-folding initiation sites are driven by hydrophobic interactions (63,64) and therefore approximately mimic the collapse process described by this HPC theory. The Description column in Table 1 indicates whether the protein is the wild-type (WT) or a mutant variant.

TABLE 1.

Experimentally determined midpoint-folding transitions for RNase A and SNase

Protein	Description	Temperature [K]	pH	Folding pressure [bar]	Reference
Ribonuclease A	WT	313	5.5	5930	(64)
	F46V	313	5.5	1740
	F46E	283	5.5	1540
	F46K	283	5.5	1020
Staphylococcal nuclease	WT	294	5.5	2047	(54)
	V66A	294	5.5	890
	WT	294	4.5	1090	(65)
	A69T+A90S	294	7.0	80

Mutations are described as: original amino-acid residue; residue location; and mutated amino-acid residue. For instance, the mutation of the 46th residue of a chain from Phe to Val is represented as F46V.

For both proteins, Table 1 shows that the WT is the most stable against pressure denaturation, while mutations, which replace a hydrophobic residue with either a less hydrophobic or polar residue, show much lower pressure stability. This behavior is attributed to the loss of stabilizing hydrophobic interactions within the chain-folding initiation site of the protein (64). It follows that a double-mutation in the hydrophobic core of two hydrophobic residues to two polar residues would create an even less stable protein, which is the case for the A69T+A90S SNase variant (65).

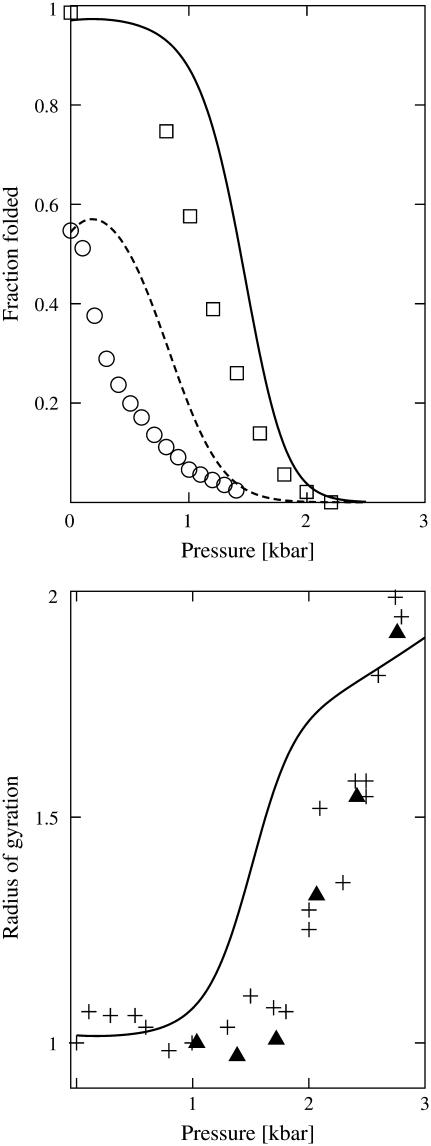
In Fig. 3, we focus on comparing the pressure-induced changes in stability and structure derived from our modified HPC theory with experiments. Specifically, we compare the stability behavior of a SNase heteropolymer in HPC theory to that of the actual SNase protein. To make the comparison, we define the following set of amino-acid residues to be hydrophobic (39): Ala, Gly, Ile, Leu, Met, Phe, Pro, Trp, Tyr, and Val, which leads to Φ = 0.411 and N_r = 150 for the WT SNase heteropolymer. While there are alternative choices for the set of hydrophobic amino acids that differ slightly from the one presented above (see, e.g., (9,48,66), they predict the same stability trends described below.

FIGURE 3.

(Top) Comparison of the fraction of folded proteins for the WT (N_r = 150, Φ = 0.411) and double-mutated SNase (N_r = 150, Φ = 0.393) heteropolymers of HPC theory (lines) with the experimental pressure stability of WT SNase at pH 4.5 (squares) and its double-mutant variant at pH 7.0 (circles) at T = 294 K (65). (Bottom) Comparison of the average radii of gyration predicted for the WT SNase heteropolymer of HPC theory (line) with WT experimental data at pH 5.5 determined by x-ray scattering (plus symbols) (67) and neutron scattering (triangles) (68). We normalize the radii of gyration by protein size at the lowest recorded pressure.

The calculated stability of the SNase heteropolymer of HPC theory shows good agreement with that of its experimental counterpart (65) (Fig. 3, top). In particular, it is able to capture the pressure-induced sigmoidal destabilization of the WT SNase protein and its double-mutant variant. For these calculations, the double-mutated SNase heteropolymer of HPC theory has the same chain length as the WT (N_r = 150) but a lower sequence hydrophobicity (Φ = 0.393). This lower value of Φ reflects the fact that the double-mutation decreases the number of hydrophobic amino-acid residues relative to the WT protein, as determined by the list of hydrophobic amino acids designated above. Although the present HPC theory does not explicitly account for pH effects necessary for a comprehensive treatment of the data, it is still able to predict the basic experimental trends that point mutations have on SNase stability.

Finally, we compare the pressure-dependence of the average radius of gyration of the WT SNase heteropolymer of HPC theory with that of the actual SNase protein determined through x-ray scattering (67) and neutron-scattering (68) (Fig. 3, bottom). As pressure is increased, the protein favors a slightly more expanded denatured state, and its radius of gyration increases accordingly. The fact that the predictions show good qualitative agreement with the experimental structural changes that occur upon pressure denaturation provides further evidence that our modified HPC theory is reproducing some of the key physical aspects of protein stability in the pressure-temperature plane.

CONCLUSIONS

We have generalized an insightful heteropolymer collapse theory, originally developed to study the temperature-dependence of protein folding, so that it can also account for pressure effects. Our generalization relies solely on the introduction of a statistical mechanical treatment for the effect of pressure on the interaction between hydrophobic amino-acid residues and water. Specifically, we have calculated the strength of the effective interaction of nonpolar amino acids with water using a molecular thermodynamic model for the interfacial free energy between liquid water and a curved hydrophobic solute. This model, which can also qualitatively reproduce water's other distinctive thermodynamic properties, predicts that the water-solute interfacial free energy is reduced by the application of large hydrostatic pressures, allowing water to penetrate into folded heteropolymers and break apart their hydrophobic cores, a physical picture that was suggested earlier by information theory calculations (28,29) and detailed molecular simulations (26,27). One consequence is that folded heteropolymers are predicted to display the kind of closed region of stability in the pressure-temperature plane exhibited by native proteins. The qualitative predictions of the theory compare well with experimental data for the stability of several proteins.

The qualitative success of our modified HPC theory appears to strengthen the argument that pressure denaturation is aided by pressure-induced weakening of hydrophobic interactions (26–29). However, as discussed in the Introduction, the contrast between this perspective and the experimentally derived view that exposure of hydrophobic residues to solvent opposes unfolding demonstrates that there are still fundamental questions left unanswered about the factors governing pressure denaturation. We also understand that this type of coarse-grained model represents proteins in a highly simplified manner and that other solvation effects (e.g., pH, charge, and salt effects), packing geometries, and folding intermediates may alter this picture of protein stability. We are currently exploring different avenues to account for these effects.