Abstract
We describe a method for recovering the underlying parametrization of scattered data (mi) lying on a manifold M embedded in high-dimensional Euclidean space. The method, Hessian-based locally linear embedding, derives from a conceptual framework of local isometry in which the manifold M, viewed as a Riemannian submanifold of the ambient Euclidean space ℝn, is locally isometric to an open, connected subset Θ of Euclidean space ℝd. Because Θ does not have to be convex, this framework is able to handle a significantly wider class of situations than the original ISOMAP algorithm. The theoretical framework revolves around a quadratic form ℋ(f) = ∫M ∥Hf(m)∥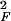 dm defined on functions f : M ↦ ℝ. Here Hf denotes the Hessian of f, and ℋ(f) averages the Frobenius norm of the Hessian over M. To define the Hessian, we use orthogonal coordinates on the tangent planes of M. The key observation is that, if M truly is locally isometric to an open, connected subset of ℝd, then ℋ(f) has a (d + 1)-dimensional null space consisting of the constant functions and a d-dimensional space of functions spanned by the original isometric coordinates. Hence, the isometric coordinates can be recovered up to a linear isometry. Our method may be viewed as a modification of locally linear embedding and our theoretical framework as a modification of the Laplacian eigenmaps framework, where we substitute a quadratic form based on the Hessian in place of one based on the Laplacian.
dm defined on functions f : M ↦ ℝ. Here Hf denotes the Hessian of f, and ℋ(f) averages the Frobenius norm of the Hessian over M. To define the Hessian, we use orthogonal coordinates on the tangent planes of M. The key observation is that, if M truly is locally isometric to an open, connected subset of ℝd, then ℋ(f) has a (d + 1)-dimensional null space consisting of the constant functions and a d-dimensional space of functions spanned by the original isometric coordinates. Hence, the isometric coordinates can be recovered up to a linear isometry. Our method may be viewed as a modification of locally linear embedding and our theoretical framework as a modification of the Laplacian eigenmaps framework, where we substitute a quadratic form based on the Hessian in place of one based on the Laplacian.
Keywords: manifold learning|ISOMAP|tangent coordinates|isometry| Laplacian eigenmaps
1. Introduction
A recent article in Science (1) proposed to recover a low-dimensional parametrization of high-dimensional data by assuming that the data lie on a manifold M which, viewed as a Riemannian submanifold of the ambient Euclidean space, is globally isometric to a convex subset of a low-dimensional Euclidean space. This bold assumption has been surprisingly fruitful, although the extent to which it holds is not fully understood.
It is now known (2, 3) that there exist high-dimensional libraries of articulated images for which the corresponding data manifold is indeed locally isometric to a subset of a Euclidean space; however, it is easy to see that, in general, the assumption that the subset will be convex is unduly restrictive. Convexity can fail in the setting of image libraries due to (i) exclusion phenomena (2, 3), where certain regions of the parameter space would correspond to collisions of objects in the image, or (ii) unsystematic data sampling, which investigates only a haphazardly chosen region of the parameter space.
In this article we describe a method that works to recover a parametrization for data lying on a manifold that is locally isometric to an open, connected subset Θ of Euclidean space ℝd. Because this subset need not be convex, whereas the original method proposed in ref. 1 demands convexity, our proposal significantly expands on the class of cases that can be solved by isometry principles.
Justification of our method follows from properties of a quadratic form ℋ(f) = ∫M ∥Hf(m)∥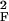 dm defined on functions f : M ↦ ℝ. ℋ(f) measures the average, over the data manifold M, of the Frobenius norm of the Hessian of f. To define the Hessian, we use orthogonal coordinates on the tangent planes of M.
dm defined on functions f : M ↦ ℝ. ℋ(f) measures the average, over the data manifold M, of the Frobenius norm of the Hessian of f. To define the Hessian, we use orthogonal coordinates on the tangent planes of M.
The key observation is that, if M is locally isometric to an open, connected subset of ℝd, then ℋ(f) has a (d + 1)-dimensional null space consisting of the constant function and a d-dimensional space of functions spanned by the original isometric coordinates. Hence, the isometric coordinates can be recovered, up to a rigid motion, from the null space of ℋ(f).
We describe an implementation of this procedure on sampled data and demonstrate that it performs consistently with the theoretical predictions on a variant of the “Swiss roll” example, where the data are not sampled from a convex region in parameter space.
2. Notation and Motivation
Suppose we have a parameter space Θ ⊂ ℝd and a smooth mapping ψ : Θ ↦ ℝn, where the embedding space ℝn obeys d < n. We speak of the image M = ψ(Θ) as the manifold, although of course from the viewpoint of manifold theory it is actually the very special case of a single coordinate patch.
The vector θ can be thought of as some control parameters underlying a measuring device and the manifold as the enumeration m = ψ(θ) of all possible measurements as the parameters vary. Thus the mapping ψ associates parameters to measurements.
In such a setting, we are interested in obtaining data examples mi, i = 1, … , N showing (we assume) the results of measurements with many different choices of control parameters (θi, i = 1, … , N). We will speak of M as the data manifold, i.e., the manifold on which our data mi must lie. In this article we consider only the situation where all data points mi lie exactly in the manifold M.
There are several concrete situations related to image analysis and acoustics where this abstract model may apply.
Scene variation: pose variations and facial gesturing;
Imaging variations: changes in the position of lighting sources and in the spectral composition of lighting color; and
Acoustic articulations: changes in distance from source to receiver, position of the speaker, or direction of the speaker's mouth.
In all such situations, there is an underlying parameter controlling articulation of the scene; here are two examples.
Facial expressions: The tonus of several facial muscles control facial expression; conceptually, a parameter vector θ records the contraction of each of those muscles.
Pose variations: Several joint angles (shoulder, elbow, wrist, etc.) control the combined pose of the elbow–wrist–finger system in combination.
We also speak of M as the articulation manifold.
In the above settings and presumably many others, we can make measurements (mi), but they are without access to the corresponding articulation parameters (θi).
It would be interesting to be able to recover the underlying parameters θi from the observed points mi on the articulation manifold. Thus we have the following.
Parametrization Recovery Problem.
Given a collection of data points (mi) on an articulation manifold M, recover the mapping ψ and the parameter points θi.
As stated, this of course is ill-posed, because if ψ is one solution, and φ : ℝd ↦ ℝd is a morphing of the Euclidean space ℝd, the combined mapping ψ ○ φ is another solution. For this reason, several extra assumptions must be made in order to uniquely determine solutions.
3. ISOMAP
In an insightful article, Tenenbaum et al. (1) proposed a method that, under certain assumptions, could indeed recover the underlying parametrization of a data manifold. The assumptions were:
(ISO1) Isometry: The mapping ψ preserves geodesic distances. That is, define a distance between two points m and m′ on the manifold according to the distance travelled by a bug walking along the manifold M according to the shortest path between m and m′. Then the isometry assumption says that
where |⋅| denotes Euclidean distance in ℝd.
(ISO2) Convexity: The parameter space Θ is a convex subset of ℝd. That is, if θ, θ′ is a pair of points in Θ, then the entire line segment {(1 − t)θ + tθ′ : t ∈ (0, 1)} lies in Θ.
Tenenbaum et al. (1) introduced a procedure, ISOMAP, which under these assumptions recovered Θ up to rigid motion. That is, up to a choice of origin and a rotation and possible mirror imaging about that origin, ISOMAP recovered Θ. In their article, they gave an example showing successful recovery of articulation parameters from an image database that showed many views of a wrist rotating and a hand opening at various combinations of rotation/opening.
The stated assumptions lead to two associated questions:
(Q1) Do interesting articulation manifolds have isometric structure?
(Q2) Are interesting parameter spaces truly convex?
We (2, 3) studied these questions in the case of image libraries. Namely, we modeled images m as continuous functions m(x, y) defined on the plane (x, y) ∈ ℝ2 and focused attention on images in special articulation families defined by certain mathematical models. As one example, we considered images of a ball on a white background, where the underlying articulation parameter is the position of the ball's center. In this model, let Bθ denote the ball of radius 1 centered at θ ∈ ℝ2, and define
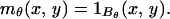 |
This establishes a correspondence between θ ∈ ℝ2 and mθ in L2(ℝ2). After dealing with technicalities associated with having L2(ℝ2) as the ambient space in which M is embedded, we derived expressions for the metric structure induced from L2(ℝ2) and showed that indeed, if Θ is a convex subset of ℝ2, then isometry holds.
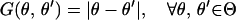 |
We found that isometry held for a dozen examples of interesting image articulation families including cartoon faces with articulated eyes, lips, and brows. Hence Q1 admits of positive answers in a number of interesting cases.
On the other hand, in our studies of image articulation families, we (2, 3) noted that Q2 can easily have a negative answer. A simple example occurs with images showing two balls that articulate by translation, as in the single-ball case mentioned above, but where the ball centers obey exclusion: The two balls never overlap. In this case, the parameter space Θ ⊂ ℝ4 becomes nonconvex; writing θ = (θ1, θ2) as a concatenation of the parameters of the two ball centers, we see that it is missing a tube where |θ1 − θ2| ≤ 1.
The case of two balls moving independently and subject to exclusion is merely one in a series of examples where the articulation manifold fails to obey ISO1 and ISO2 but instead obeys something weaker.
(LocISO1) Local isometry: In a small enough neighborhood of each point m, geodesic distances to nearby points m′ in M are identical to Euclidean distances between the corresponding parameter points θ and θ′.
(LocISO2) Connectedness: The parameter space Θ is an open, connected subset of ℝd.
In such settings, the original assumptions of ISOMAP are violated, and as shown (ref. 2 and unpublished data), the method itself fails to recover the parameter space up to a linear mapping. We (unpublished data) pointed out the possibility of recovering nonconvex Θ by applying ISOMAP to a suitable decomposition of M into overlapping geodesically convex pieces. However, a fully automatic procedure based on a general principle would be preferable in solving this problem. In this article we propose such a procedure.
4. The ℋ Functional
We now set up notation to define the quadratic form ℋ(f) referred to in the Abstract and Introduction.
We suppose that M ⊂ ℝn is a smooth manifold, and thus the tangent space Tm(M) is well defined at each point m ∈ M. Thinking of the tangent space as a subspace of ℝn, we can associate to each such tangent space Tm(M) ⊂ ℝn an orthonormal coordinate system using the inner product inherited from ℝn. (It will not matter in the least how this choice of coordinate system varies from point to point in M.)
Think momentarily of Tm(M) as an affine subspace of ℝn that is tangent to M at m, with the origin 0 ∈ Tm(M) identified with m ∈ M. There is a neighborhood Nm of m such that each point m′ ∈ Nm has a unique closest point v′ ∈ Tm(M) and such that the implied mapping m′ ↦ v′ is smooth. The point in Tm(M) has coordinates given by our choice of orthonormal coordinates for Tm(M). In this way, we obtain local coordinates for a neighborhood Nm of m ∈ M, call them x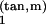 , … , x
, … , x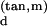 , where we retain tan, m in the notation to remind us that they depend on the way in which coordinates were defined on Tm(M).
, where we retain tan, m in the notation to remind us that they depend on the way in which coordinates were defined on Tm(M).
We now use the local coordinates to define the Hessian of a function f : M ↦ ℝ that is C2 near m. Suppose that m′ ∈ Nm has local coordinates x = x(tan,m). Then the rule g(x) = f(m′) defines a function g : U ↦ ℝ, where U is a neighborhood of 0 in ℝd. Because the mapping m′ ↦ x is smooth, the function g is C2. We define the Hessian of f at m in tangent coordinates as the ordinary Hessian of g.
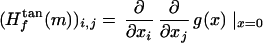 |
In short, at each point m, we use the tangent coordinates and differentiate f in that coordinate system. We call this construction the tangent Hessian for short.
We now consider a quadratic form defined on C2 functions by
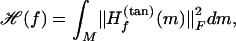 |
where dm stands for a probability measure on M that has strictly positive density everywhere on the interior of M. ℋ(f) measures the average “curviness” of f over the manifold M.
Theorem.
Suppose M = ψ(Θ) where Θ is an open, connected subset of ℝd, and ψ is a locally isometric embedding of Θ into ℝn. Then ℋ(f) has a (d + 1)-dimensional null space consisting of the constant function and a d-dimensional space of functions spanned by the original isometric coordinates.
We give the proof in Appendix.
Corollary.
Under the same assumptions as Theorem, the original isometric coordinates θ can be recovered, up to a rigid motion, by identifying a suitable basis for the null space of ℋ(f).
5. Hessian Locally Linear Embedding (HLLE)
We now consider the setting where we have sampled data (mi) lying on M, and we would like to recover the underlying parametrization ψ and underlying parameter settings θi, at least up to rigid motion. The Theorem and its Corollary suggest the following algorithm for attacking this problem. We model our algorithm structure on the original LLE algorithm (4).
HLLE algorithm:
Input: (mi : i = 1, … , N) a collection of N points in ℝn.
Parameters: d, the dimension of the parameter space; k, the size of the neighborhoods for fitting.
Constraints: min(k, n) > d.
Output: (wi : i = 1, … , N) a collection of N points in ℝd, the recovered parametrization.
Procedure:
Identify neighbors: For each data point mi, i = 1, … n, identify the indices corresponding to the k-nearest neighbors in Euclidean distance. Let 𝒩i denote the collection of those neighbors. For each neighborhood 𝒩i, i = 1, … , N, form a k × n matrix Mi with rows that consist of the recentered points mj − m̄i, j ∈ 𝒩i, where m̄i = Ave{mj : j ∈ 𝒩i}.
Obtain tangent coordinates: Perform a singular value decomposition of Mi, getting matrices U, D, and V; U is k by min(k, n). The first d columns of U give the tangent coordinates of points in 𝒩i.
Develop Hessian estimator: Develop the infrastructure for least-squares estimation of the Hessian. In essence, this is a matrix Hi with the property that if f is a smooth function f : M ↦ ℝ, and fj = (f(mi)), then the vector vi with entries that are obtained from f by extracting those entries corresponding to points in the neighborhood 𝒩i; then, the matrix vector product Hivi gives a d(d + 1)/2 vector with entries that approximate the entries of the Hessian matrix, (∂f/∂Ui∂Uj).
- Develop quadratic form: Build a symmetric matrix ℋij having, in coordinate pair ij, the entry
Here by Hl we mean, again, the d(d + 1)/2 × k matrix associated with estimating the Hessian over neighborhood 𝒩l, where rows r correspond to specific entries in the Hessian matrix and columns i correspond to specific points in the neighborhood.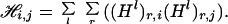
Find approximate null space: Perform an eigenanalysis of ℋ, and identify the (d + 1)-dimensional subspace corresponding to the d + 1 smallest eigenvalues. There will be an eigenvalue 0 associated with the subspace of constant functions; and the next d eigenvalues will correspond to eigenvectors spanning a d-dimensional space V̂d in which our embedding coordinates are to be found.
Find basis for null space: Select a basis for V̂d, which has the property that its restriction to a specific fixed neighborhood 𝒩0 (the neighborhood may be chosen arbitrarily from those used in the algorithm) provides an orthonormal basis. The given basis has basis vectors w1, … wd; these are the embedding coordinates.
The algorithm is a straightforward implementation of the idea of estimating tangent coordinates, the tangent Hessian, and the empirical version of the operator ℋ.
Remarks:
Coding requirements: This can be implemented easily in matlab, mathematica, s-plus, r, or similar quantitative programming environment; our matlab implementation is available at http://basis.stanford.edu/HLLE.
Storage requirements: This is a “spectral method” and involves solving the eigenvalue problem for an N × N matrix. Although it would appear to require O(N2) storage, which can be prohibitive, the storage required is actually proportional to n⋅N, i.e. the storage of the data points. In fact, this storage can be kept on disk; the remaining storage is basically proportional to Nk. Note that the matrix ℋ is a sparse matrix with ≈O(Nk) nonzero entries.
Computational complexity: In effect, the computational cost difference between a sparse and a full matrix using the sparse eigenanalysis implementation in matlab 6.1 (using Arnoldi methods) depends on the cost of computing a matrix-vector product using the input matrix. For our sparse matrix, the cost of each product is ≈2kN, whereas for a full matrix the cost is ≈2N2, making the overall cost of the sparse version O(kN2).
- Building the Hessian estimator: Consider first the case d = 2. Form a matrix Xi consisting of the following columns.
In the general case d > 2, create a matrix with 1 + d + d(d + 1)/2 columns; the first d + 1 of these consist of a vector of ones, and then the first d columns of U, and the last d(d + 1)/2 consist of the various cross products and squares of those d columns. Perform the usual Gram–Schmidt orthonormalization process on the matrix Xi, yielding a matrix X̃i with orthonormal columns; then define Hi by extracting the last d(d + 1)/2 columns and transposing.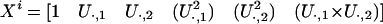
1 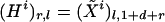
- Finding the basis for the null space: Let V be the N × d matrix of eigenvectors built from the nonconstant eigenvectors associated to the (d + 1) smallest eigenvalues, and let Vl,r denote the lth entry in the rth eigenvector of ℋ. Define the matrix (R)rs = ∑j∈N1 Vj,rVj,s. The desired N × d matrix of embedding coordinates is obtained from
In section 7, we apply this recipe to a canonical isometric example.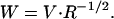
6. Comparison to LLE/Laplacian Eigenmaps
The algorithm we have described bears substantial resemblance to the LLE procedure proposed by Roweis and Saul (4). The theoretical framework we have described also bears substantial resemblance to the Laplacian eigenmap framework of Belkin and Niyogi (5), only with the Hessian replacing the Laplacian. The Laplacian eigenmap setup goes as follows: Define the Laplacian operator in tangent coordinates by Δ(tan)(f) = ∑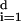 (∂2f/∂x
(∂2f/∂x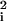 ), and define the functional ℒ(f) = ∫M(Δ(tan)(f))2dm. This functional computes the average of the Laplacian operator over the manifold; Laplacian eigenmap methods propose to solve embedding problems by obtaining the d + 1 lowest eigenvalues of ℒ and using the corresponding eigenfunctions to embed the data in low-dimensional space. The LLE method is an empirical implementation of the same principle, defining a discrete Laplacian based on a nearest-neighbor graph and embedding scattered n-dimensional data by using the first d nonconstant eigenvectors of the graph Laplacian.
), and define the functional ℒ(f) = ∫M(Δ(tan)(f))2dm. This functional computes the average of the Laplacian operator over the manifold; Laplacian eigenmap methods propose to solve embedding problems by obtaining the d + 1 lowest eigenvalues of ℒ and using the corresponding eigenfunctions to embed the data in low-dimensional space. The LLE method is an empirical implementation of the same principle, defining a discrete Laplacian based on a nearest-neighbor graph and embedding scattered n-dimensional data by using the first d nonconstant eigenvectors of the graph Laplacian.
7. Data Example
In this example we take a random sample (mi) on the Swiss roll surface (4) in three dimensions. The resulting surface is like a rolled-up sheet of paper and thus is exactly isometric to Euclidean space (i.e. to a rectangular segment of ℝ2). Successful results of LLE and ISOMAP on such data have been published (1, 4). However, here we consider a change in sampling procedure. Instead of sampling parameters in a full rectangle, we sample from a rectangle with a missing rectangular strip punched out of the center. The resulting Swiss roll is then missing the corresponding strip and thus is not convex (while still remaining connected).
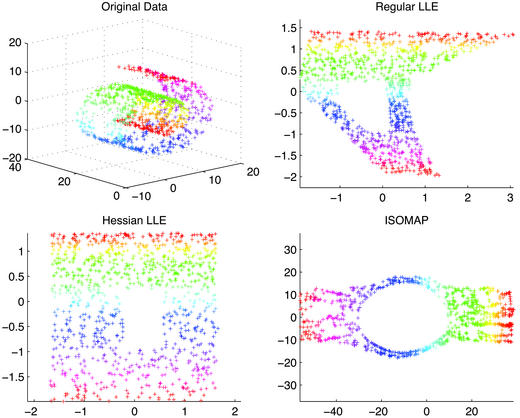
Using this model and the code provided for ISOMAP and LLE in refs. 1 and 4, respectively, we test the performance of all three algorithms on a random sample of 600 points in three dimensions. The points were generated by using the same code published by Roweis and Saul (4). The results, as seen in Fig. 1, show the dramatic effect that nonconvexity can have on the resulting embeddings. Although the data manifold is still locally isometric to Euclidean space, the effect of the missing sampling region is, in the case of LLE, to make the resulting embedding functions asymmetric and nonlinear with respect to the original parametrization. In the case of ISOMAP, the nonconvexity causes a strong dilation of the missing region, warping the rest of the embedding. Hessian LLE, on the other hand, embeds the result almost perfectly into two-dimensional space.
Figure 1.
(Upper Left) Original data. (Upper Right) LLE embedding (Roweis and Saul code, k = 12; ref. 4). (Lower Left) Hessian eigenmaps (Donoho and Grimes code, k = 12; as described in section 5). (Lower Right) ISOMAP (Tenenbaum et al. code, k = 7; ref. 1). The underlying correct parameter space that generated the data is a square with a central square removed, similar to what is obtained by the Hessian approach (Lower Left).
The computational demands of LLE algorithms are very different than those of the ISOMAP distance-processing step. LLE and HLLE are both capable of handling large N problems, because initial computations are performed only on smaller neighborhoods, whereas ISOMAP has to compute a full matrix of graph distances for the initial distance-processing step. However, both LLE and HLLE are more sensitive to the dimensionality of the data space, n, because they must estimate a local tangent space at each point. Although we introduce an orthogonalization step in HLLE that makes the local fits more robust to pathological neighborhoods than LLE, HLLE still requires effectively a numerical second differencing at each point that can be very noisy at low sampling density.
8. Discussion
We have derived an LLE algorithm from a conceptual framework that provably solves the problem of recovering a locally isometric parametrization of a manifold M when such a parametrization is possible. The existing ISOMAP method can solve the same problem in the special case where M admits a globally isometric parametrization. This special case requires that M be geodesically convex or equivalently that Θ be convex.
Note that in dealing with data points (mi) sampled from a naturally occurring manifold M, we can see no reason that the probability measure underlying the sampling must have geodesically convex support. Hence our local isometry assumption seems much more likely to hold in practice than the more restrictive global isometry assumption in ISOMAP.
HLLE requires the solution of N separate k × k eigenproblems and, similar to Roweis and Saul's original LLE algorithm, a single N × N sparse eigenproblem. The sparsity of this eigenproblem can confer a substantial advantage over the general nonsparse eigenproblem. This is an important factor distinguishing LLE techniques from the ISOMAP technique, which poses a completely dense N × N matrix for eigenanalysis. In our experience, if we budget an equal programming effort in the two implementations, the implementation of HLLE can solve much larger-scale data analysis problems (much larger N) than ISOMAP. [We are aware that there are modifications of the ISOMAP principle under development that attempt to take advantage of sparse graph structure (i.e. landmark ISOMAP); however, the original ISOMAP principle discussed here is not posable as a sparse eigenproblem.]
A drawback of HLLE versus the other methods just discussed is the Hessian approach requires estimation of second derivatives, and this is known to be numerically noisy or difficult in very high-dimensional data samples.
Our understanding of the phenomena involved in learning parametrizations is certainly not complete, and we still have much to learn about the implementation of spectral methods for particular types of data problems.
Acknowledgments
We thank Lawrence Saul (University of Pennsylvania, Philadelphia) for extensive discussions of both LLE and ISOMAP and also both George Papanicolaou (Stanford University) for pointers and Jonathan Kaplan (Harvard University, Cambridge, MA) for extensive discussions about properties of ill-posed boundary-value problems. D.L.D. thanks R. R. Coifman (Yale University, New Haven, CT) for pointing out the intrinsic interest of LLE and ISOMAP as well as for helpful discussions and references. C.G. thanks Vin de Silva (Stanford University) for extensive discussions of both LLE and ISOMAP. This work was partially supported by National Science Foundation Grants DMS-0077261, DMS-0140698, and ANI-008584 and a contract from the Defense Advanced Research Projects Agency Applied and Computational Mathematics Program.
Abbreviations
- LLE
locally linear embedding
- HLLE
Hessian LLE
Proof of Our Theorem
Because the mapping ψ is a locally isometric embedding, the inverse mapping φ = ψ−1 : M ↦ ℝd provides a locally isometric coordinate system on M. Let θ1, … , θd denote the isometric coordinates.
Let m be a fixed point in the interior of M, and let f be a C2 function on M. Define the pullback of f to Θ by g(θ) = f(ψ(θ)). Define the Hessian in isometric coordinates of f at m by
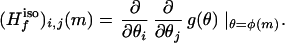 |
This definition postulates knowledge of the underlying isometry φ, so the result is definitely not something we expect to be “learnable” from knowledge of M alone. Nevertheless, it provides an important benchmark for comparison. Now define the quadratic form
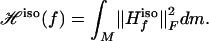 |
This is similar to the quadratic form ℋ except that it is based on the Hessian in isometric coordinates rather than the Hessian in tangent coordinates. We will explore the null space of this quadratic form and relate it to the null space of ℋ.
By its very definition, ℋiso has a natural pullback from L2(M, dm) to L2(Θ, dθ). Indeed, letting g : Θ ↦ ℝ be a function on Θ ⊂ ℝd with open interior, letting θ be an interior point, and letting H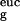 (θ) denote the ordinary Hessian in Euclidean coordinates at θ, we have actually defined Hiso by H
(θ) denote the ordinary Hessian in Euclidean coordinates at θ, we have actually defined Hiso by H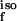 ≡ H
≡ H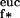 , where f*(θ) = f(ψ(θ)) is the pullback of f to Θ ⊂ ℝd. Hence defining, for functions g : Θ ↦ ℝ, the quadratic form
, where f*(θ) = f(ψ(θ)) is the pullback of f to Θ ⊂ ℝd. Hence defining, for functions g : Θ ↦ ℝ, the quadratic form
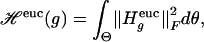 |
(where dθ and dm are densities in one-to-one correspondence under the one-to-one correspondence θ ↔ m), we have
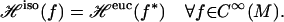 |
It follows that the null space of ℋiso is in one-to-one correspondence with the null space of ℋeuc under the pullback by ψ. Consider then the null space of ℋeuc.
Lemma 1.
Let Θ ⊂ ℝd be connected with open interior, and let dθ denote a strictly positive density on the interior of Θ. Let W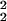 (Θ) denote the usual Sobolev space of functions on Θ that have finite L2 norm and the first two distributional derivatives of which exist and belong to L2. Then ℋeuc, viewed as a functional on the linear space W
(Θ) denote the usual Sobolev space of functions on Θ that have finite L2 norm and the first two distributional derivatives of which exist and belong to L2. Then ℋeuc, viewed as a functional on the linear space W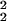 (Θ), has a (d + 1)-dimensional null space consisting of the span of the constant function together with the d coordinate functions θ1, … , θd.
(Θ), has a (d + 1)-dimensional null space consisting of the span of the constant function together with the d coordinate functions θ1, … , θd.
Proof:
It of course is obvious that the null space contains the span of the constant function and all the coordinate functions, because this span is simply all linear functions and linear functions have everywhere-vanishing Hessians. In the other direction, we show that the null space contains only these functions. Consider any function g in C∞(Θ) that is not exactly linear. Then there must be some second-order mixed derivative (∂g/∂θi1∂θi2) that is nonvanishing on some ball: ∥∂g/∂θi1∂θi2∥L2(Θ,dθ) > 0. But,
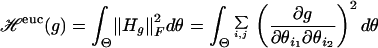 |
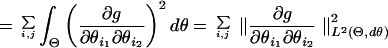 |
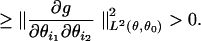 |
Hence no smooth nonlinear function can belong to the null space of ℋeuc. The openness of the interior of Θ implies that C∞(Θ) is dense in W (Θ), and thus we can reach the same conclusion for all g in W
(Θ), and thus we can reach the same conclusion for all g in W (Θ).
(Θ).
By pullback, Lemma 1 immediately implies:
Corollary.
Viewed as a functional on W (M), ℋiso has a (d + 1)-dimensional null space consisting of the span of the constant functions and the d-isometric coordinates θi(m) on M.
(M), ℋiso has a (d + 1)-dimensional null space consisting of the span of the constant functions and the d-isometric coordinates θi(m) on M.
We now show the same for the object of our original interest: ℋ. This follows immediately from the following lemma.
Lemma 2.
Let f be a function in C∞(M), and let ψ be a local isometry between Θ and M. Then at every m ∈ interior(M),
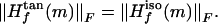 |
Lemma 2 implies that
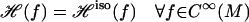 |
and allows us to see that ℋ and ℋiso have the same null space. Our theorem follows.
Proof:
Recall that ∥H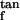 (m)∥F is unchanged by variations in the choice of orthonormal basis for the tangent plane Tm(M). Recall that φ = ψ−1 is a local isometry and gives a coordinate system θ1, … , θd on M and therefore induces a choice of coordinate system on Tm(M) that is orthonormal, because φ is a local isometry. Therefore we may assume that our choice of orthonormal basis for Tm(M) is exactly the same as the choice induced by φ. Once this choice has been made, Lemma 2 follows if we can show that
(m)∥F is unchanged by variations in the choice of orthonormal basis for the tangent plane Tm(M). Recall that φ = ψ−1 is a local isometry and gives a coordinate system θ1, … , θd on M and therefore induces a choice of coordinate system on Tm(M) that is orthonormal, because φ is a local isometry. Therefore we may assume that our choice of orthonormal basis for Tm(M) is exactly the same as the choice induced by φ. Once this choice has been made, Lemma 2 follows if we can show that
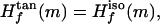 |
A1 |
which will follow if we show that for every vector v ∈ Tm(M),
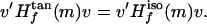 |
A2 |
Given a vector v ∈ Tm(M), let γv : [0, ɛ) ↦ M denote the unit-speed geodesic in M that starts at m = γv(0) and that has v for its tangent (d/dt)γv|t=0 = v. Consider the induced function ggeo,v(t) = f(γv(t)). Notice that by definition of isometric coordinates
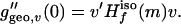 |
On the other hand, the tangent space Tm(M) provides another local coordinate system for M. Let τm : Tm(M) ↦ M denote the inverse that maps from local coordinates back to M; this is the inverse of the mapping m′ ↦ (x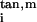 (m′)). Consider the path δv : [0, ɛ) ↦ Tm(M) defined by dv(t) = tv, which this corresponds to a path in M defined by δv(t) = τm(dv(t)), i.e. projecting the path in Tm(M) onto a neighborhood of m in M. Consider the induced function gtan,v = f(δv(t)). Notice that by definition of tangent coordinates
(m′)). Consider the path δv : [0, ɛ) ↦ Tm(M) defined by dv(t) = tv, which this corresponds to a path in M defined by δv(t) = τm(dv(t)), i.e. projecting the path in Tm(M) onto a neighborhood of m in M. Consider the induced function gtan,v = f(δv(t)). Notice that by definition of tangent coordinates
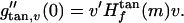 |
Hence we have to show that
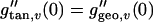 |
A3 |
for all v ∈ Tm(M). This implies Eq. A2 and hence Eq. A1.
The key observation is that
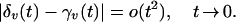 |
A4 |
It follows that for every Lipschitz f that
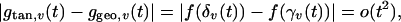 |
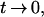 |
which proves Eq. A3. The key relation (Eq. A4) follows by combining two basic facts.
Lemma 3.
Consider a geodesic γ : [0, ɛ) ↦ M of a Riemannian submanifold M of ℝn and view it as a space curve in ℝn. View Tm(M) as a subspace of ℝn. The acceleration vector (d2/dt2)γ of this space curve at the point m = γ(0) is normal to Tm(M).
Lemma 3 is a classic textbook fact about isometric embeddings (see chapter 6 of ref. 6). Less well known is that the same fact is true of δv(t).
Lemma 4.
Viewing t ↦ δv(t) as a space curve in ℝn, its acceleration vector at t = 0 is normal to Tm(M).
In short, the acceleration components of both δv and γv at 0 reflect merely the extrinsic curvature of M as a curved submanifold of ℝn; neither curve has an acceleration component within Tm(M). Because both curves by construction have the same tangent at 0, namely v, the key relation (Eq. A4) holds, and Lemma 2 is proved. Lemma 4 does not seem to be as well known as Lemma 3, so we prove it here.
Proof:
Let c = n − d denote the codimension of M in ℝn. We can model M in the vicinity of m as the solution of a system of equations.
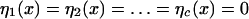 |
Let t ↦ x(t) be a path in ℝn that starts in M at t = 0 and stays in M. Without loss of generality choose coordinates such that x(0) = 0 ∈ ℝn. Then
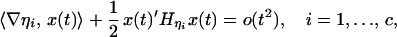 |
where ∇ηi denotes the gradient of ηi, and Hηi denotes the Hessian of ηi, both evaluated at x = 0. Writing x(t) = tv + (t2/2)u + o(t2), we conclude that
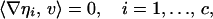 |
whereas
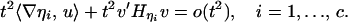 |
In short,
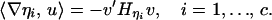 |
A5 |
Because the ∇ηi span the normal space to M at m, it follows that u must have the specified coordinates in the normal space.
Now, by definition, δv(t) is the closest point in M to the point in the tangent plane represented by tv. But then, viewing v ∈ Tm(M) as a vector in ℝn, we must have that u ∈ ℝn satisfies
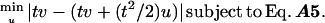 |
In short, u solves
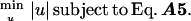 |
This minimum-norm problem has a unique solution, with u in the span of the vectors ∇ηi, i.e. in the normal space perpendicular to Tm(M). Hence the space curve x(t) has no component of acceleration in Tm(M).
References
- 1.Tenenbaum J B, de Silva V, Langford J C. Science. 2000;290:2319–2323. doi: 10.1126/science.290.5500.2319. [DOI] [PubMed] [Google Scholar]
- 2.Donoho D L, Grimes C. Technical Report 2002-27. Stanford, CA: Dept. of Statistics, Stanford University; 2002. [Google Scholar]
- 3.Donoho D L, Grimes C. Proceedings of the European Symposium on Artificial Neural Networks. Vol. 10. Evere, Belgium: d-side; 2002. pp. 199–204. [Google Scholar]
- 4.Roweis S T, Saul L K. Science. 2000;290:2323–2326. doi: 10.1126/science.290.5500.2323. [DOI] [PubMed] [Google Scholar]
- 5.Belkin M, Niyogi P. In: Advances in Neural Information Processing Systems. Dietterich T G, Becker S, Ghahramani Z, editors. Vol. 14. Cambridge, MA: MIT Press; 2002. pp. 585–591. [Google Scholar]
- 6.Do Carmo M P. In: Riemannian Geometry. Kadison R V, Singer I M, editors. Boston: Birkhäuser; 1992. pp. 124–143. [Google Scholar]