Dual-frequency 2D-IR spectroscopy heterodyned photon echo of the peptide bond

Abstract

The structure fluctuations of the peptide bond interacting with solvent are examined through the coupling and correlations of the frequency distributions of amide I and amide II transitions. The fluctuations of the two modes are anticorrelated as a result of the solvent-induced changes in the mixing of the dominant valence-bond structures of the peptide. Significant anharmonic coupling of the two modes is seen. The results are the application of a new approach to two-dimensional infrared (2D-IR) spectroscopy in which the pulse sequences used to produce the vibrational echoes incorporate two frequencies. This dual-frequency arrangement greatly extends the capabilities of 2D-IR spectroscopy by allowing the coupling between widely separated modes to be characterized in analogy with heteronuclear NMR. The experiment exposes the cross peaks, representing the mode coupling, free of the interference of the strong diagonal peaks that typically dominate 2D-IR spectroscopy. The alignment and dephasing of coupled transitions, in this example the amide I and amide II transition dipoles, is also determined by these experiments.

Multidimensional IR spectroscopy, in particular 2D-IR spectroscopy, is a powerful new method with which to obtain the time dependence of structural features of complex molecular systems, including peptides and proteins, under ambient conditions in solutions (1–7). Furthermore, the methods allow the determination of key parameters of the anharmonic potential surfaces of peptides and hence provide important tests of theoretical calculations of molecular structure and dynamics (8, 9). These coherent nonlinear IR techniques permit experimental determination of the coupling and angular relations of vibrators by using experimental protocols that are analogous to those developed for NMR. The first such experiments concerned the amide I modes of peptides, which are mainly C⩵O vibrators (1–5, 10–12). In such cases all of the relevant frequencies of an interacting ensemble of modes could readily be bracketed by the spectral bandwidth of 120-fs IR laser pulses. The response of such a system to sequences of three pulses, each with the same center frequency in the amide I region, gave rise to coherent signals, the 2D and 3D correlation spectra of which yielded the relevant structural and dynamical information. In a recent advance, 2D-IR spectroscopy experiments incorporating two pulses with different frequencies, one in the N—H and the other in the amide I region of peptides, were successful in measuring the coupling and angular relations between N—H and C⩵O modes in some simple peptides (13–15).

In this article we report a dual-frequency 2D-IR spectroscopy heterodyned photon-echo experiment. The 2D-IR spectra, which require manipulation of the vibrational coherences by the interaction of short laser pulses with inhomogeneously broadened distributions of transition frequencies, consist of diagonal features and cross peaks. The diagonal peaks are independent properties of each of the anharmonic modes, but they do not readily provide the correlations between modes that relate to 3D structure. On the other hand, the cross peaks are present only when the modes are interacting, and they contain the information essential to determining structure and structure distributions. In 2D-IR spectra the diagonal peaks are often much stronger than and interfere with the cross peaks, so it is important to find methods that can eliminate them from the signals. One such approach is to choose polarization conditions for the laser pulses involved in the heterodyne echo experiment that entirely eliminate diagonal contributions (16, 17). However, a new type of experiment is needed that effects this elimination and permits measurements of the correlations of modes that are widely separated in frequency. The dual-frequency IR echo experiment reported in this article has this purpose. It allows, if necessary, the complete elimination of the diagonal peaks from the 2D-IR spectra and focuses attention on the coupling, frequency distributions and angular relations between pairs of modes.

Methods

IR Pulse Generation.

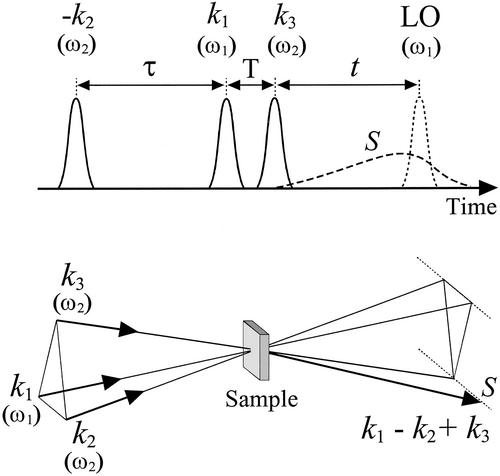
The dual-frequency 2D-IR spectroscopy experiment uses a Ti:Sapphire laser system (Clark-MXR CPA2001) to provide IR laser pulses at 775 nm with a 130-fs pulse duration and 700-μJ pulse energy to pump an optical parametric amplifier. The total output of the optical parametric amplifier was 70 μJ per pulse, which was split into two parts to enable pumping of two difference frequency generators, which produced independently tunable, phase-locked mid-IR pulses. For the given optical parametric amplifier frequency the tuning range in the 6-μm region was 150 cm⁻¹. In the N-methylacetamide (NMA) experiment, one difference frequency generator produced IR pulses of 0.15 μJ per pulse with a central frequency ω₁ = 1,675 cm⁻¹ propagating toward the sample in direction k₁ (Fig. 1) and local oscillator pulses having 0.01 μJ per pulse, the latter being further attenuated before use. The output of the second difference frequency generator (≈0.3 μJ per pulse) was split into two equal parts to generate two IR beams with central frequency ω₂ = 1,540 cm⁻¹ for the NMA experiment and vector directions k₂ and k₃. A half-wave plate and a wire-grid polarizer controlled the polarization vector of each beam. The intensities of each of the pulses were measured accurately to be used in the spectral simulations. A mercury-cadmium-telluride detector (EG & G, Judson, PA) recorded the sum of the field generated in the k₁ − k₂ + k₃ direction and the local oscillator field (Fig. 1), and the heterodyned signal was processed.

Figure 1.

(Upper) Time sequence of the dual-frequency three-pulse photon-echo experiment. S (dashed line) is a typical signal envelope. LO denotes the local oscillator pulse. (Lower) The spatial arrangement of the three beams interacting with the sample. The pulse intervals used in the text are indicated. The signal envelope is observed in the k₁ − k₂ + k₃ direction.

Beam Configurations.

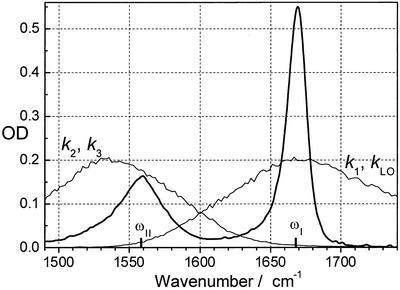
The IR beams were tuned such that one is centered on the amide I band of NMA (k₁, ω₁), and the other is close to the amide II band (k₂ and k₃, ω₂) (Fig. 2). If the spectra of these pulses at ω₁ and ω₂ are chosen to have no overlap, then there can be no diagonal peak in the direction k₁ − k₂ + k₃, because the generated field must be in the frequency range of ω_I − ω_II + ω_II = ω_I. However, the intensities of the k₂ and k₃ beams centered at the amide I band were chosen to have ≈8% of their peak values at the frequency of the amide II band. Similarly, the intensity of the k₁ beam centered at the amide II band presented a small fraction (≈4%) of its peak value at the amide I band region. These small contributions of band overlap enabled weak diagonal amide I and amide II reference peaks to be recorded in the 2D-IR spectra in addition to the dominant cross peak.

Figure 2.

The linear spectrum on an optical density (OD) scale of NMA in DMSO. The laser spectra centered near ω_I and ω_II are shown also. LO, local oscillator pulse.

Three-Pulse Integrated Photon Echo.

In the integrated three-pulse echo experiment all three pulses have the same frequency, either ω_I or ω_II. The echo signal at each chosen value of τ and T is sent directly to a detector without heterodyning and integrated over the time interval t by the response time of a detector in a manner that has already been described in detail (18–20). The grid of (τ, T) data was globally fitted to obtain the time-correlation functions of the vibrational frequencies that are required to interpret the cross-peak data obtained by 2D-IR spectroscopy. The integrated echo of NMA-D was studied previously in ²H₂O (4).

Dual-Frequency Heterodyned Transient Grating.

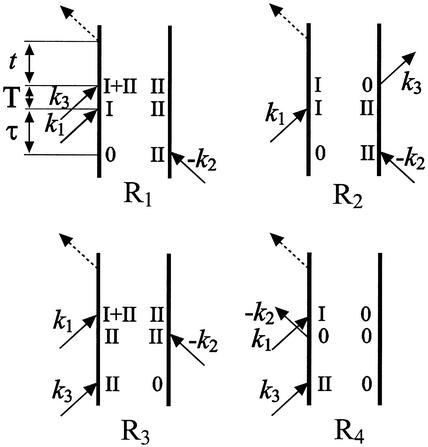
The interval τ is fixed at zero in this experiment such that a linear combination of amide I and II transitions is prepared (see Fig. 3). This coherence is transferred after an interval T. The signal is obtained as a function of T and t. Fourier transformation along t yields a time-dependent transient-grating spectrum in the region of the amide I band that oscillates with the frequency difference of the amide I and II transitions.

Figure 3.

Liouville pathways contributing to the cross peak in the rephasing (R₁ and R₂) and nonrephasing (R₃ and R₄) IR-pulse sequences.

Beam Coherence.

When the beams from both difference frequency generators were combined in a Michelson interferometer and sent to a monochromator a strong spectral interferogram was observed when the delay between the two pulses was scanned. These interferograms depended on the choice of the center frequencies of the two pulses, and the measurements served to verify the stability of the phase difference of the two sources persisting over periods of many hours. The frequency dependence of the phase of each pulse was not measured, but it was verified that phase variations expected from the optical materials used did not affect the conclusions. Comparable phase stability was not yet achieved when pulses from two optical parametric amplifiers were combined in the interferometer.

Sample.

The sample was a 150 mM solution of NMA in DMSO contained in a CaF₂ cell having a path length of 25 μm. The linear IR spectrum is shown in Fig. 2.

Modeling the 2D-IR Spectra.

In the 2D-IR experiment on NMA we chose the time delay between the second two of the incident sequence of three pulses to be zero. Thus in the limit of large-frequency bandwidth there are only two times in the problem: τ, the delay between the first pulse and the second pair; and t, the period of free evolution between the second pair and the local oscillator pulse. We used two different pulse sequences in the experiment that we refer to as rephasing and nonrephasing sequences. For the rephasing sequence the k₁ (ω₁) and k₃ (ω₂) were at a fixed zero delay, and the k₂ (ω₂) pulse delay was scanned. In the nonrephasing sequence the k₁ (ω₁) and k₂ (ω₂) beams were at a fixed time delay of zero, and the k₃ (ω₂) pulse was scanned. These scans generated the τ-axis data. Heterodyned photon-echo signals were recorded for every delay τ by scanning the local oscillator pulse over a time interval t of ≈2 ps in steps of 10 fs. The experimental 2D matrix S(τ, t) was double Fourier transformed along t and τ to generate a complex 2D-IR spectrum, S̃(ω_τ, ω_t).

The pathways that produce the cross peak for the rephasing (R₁ and R₂) and nonrephasing (R₃ and R₄) sequence experiments are illustrated in Fig. 3. These diagrams represent time lines for the interaction of successive pulses with a molecule in the sample for the particular set of vector directions of the incident pulses (21). In Fig. 3 the symbols I and II refer to the amide I or amide II excitations, and the combination of left and right indices at any vertical position along the time line represents the coherence existing at that time. For example, the system begins in an amide II transition coherence. After the interaction with the pulse in direction k₁ in diagram R₂ of Fig. 3 the system is in a coherent superposition of I and II vibrational states. Pulse k₃ completes the coherence transfer to the amide I transition. The index I + II in diagrams R₁ and R₃ corresponds to the combination state of the amide I and amide II modes. As indicated above, in the 2D-IR spectroscopy experiments the value of T, shown in Fig. 3 as the delay between k₁ and k₃ in the rephasing experiment or between k₁ and k₂ in the nonrephasing experiment, was set equal to zero.

An analysis of the integrated three-pulse echo signal yielded the vibrational frequency correlation functions for the vibrators (data not shown). The fast component of the correlation function is the correlation time of a motionally narrowed contribution to the line width. After the fast decay the correlation function and peak shifts (18) showed the decay on the few-picosecond time scale, whereas a plateau indicates a static distribution of structures. Up to ≈500 fs, during which the 2D-IR signals are strongest, the decay is slow enough for us to interpret the data in terms of a Bloch dynamics theory (5), which permits a simplification of the expressions for the 2D-IR spectrum. Inclusion of the evident spectral diffusion in the modeling did not change the results significantly.

According to the theory of 2D-IR spectroscopy (5, 22, 23) the cross-peak signal in the Bloch approximation obtained by adding results from the rephasing S_R(τ,t) and nonrephasing S_NR(τ, t) pulse sequences is predicted to be

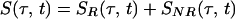1

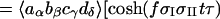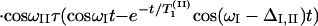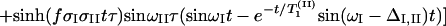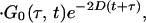where the conventional Bloch relaxation function is G₀(t, τ) given by

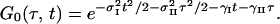The parameters ω_I and ω_II are the angular frequencies (i.e., ω/2πc is the frequency in cm⁻¹) and σ_I and σ_II the inhomogeneous widths of the amide I and amide II transitions, the T₁ values are the population relaxation times of the indicated states, D is the rotational diffusion coefficient, and the γ values are the total homogeneous dephasing rates of the amide I and amide II fundamental transitions. The correlation coefficient between the static distributions of amide I and amide II frequencies is given by f = 〈x_Ix_II〉/σ_Iσ_II, where x is the frequency deviation from the mean of the indicated frequency distribution. The time-independent polarization anisotropy (16) is given by the product of direction cosines 〈a_αb_βc_γd_δ〉, where the first through fourth pulses, polarized a, b, c, and d in the laboratory frame, excite the transition dipoles α to γ in the molecular frame. The off-diagonal anharmonicity is Δ_I,II, chosen such that the frequency of the transition between II and I + II is ω_I − Δ_I,II. By inspection of Eq. 1 the real part of the 2D-IR spectrum, obtained from the double Fourier transform of S(τ, t), displays peaks (ω_II, ω_I) and (ω_II, ω_I − Δ_I,II). In practice, a state to which the amide II population relaxes was also included in the pathways in the manner of figure 2 in ref. 13.

When f = 0, the case of uncorrelated distributions, the signal with cosh = 1 and sinh = 0 reduces to the difference between two components having opposite signs that are slightly displaced (by Δ_I,II) along the ω_t axis. The node separating the positive and negative parts of the 2D spectrum is then parallel to the ω_τ axis in the region of ω_τ = ω_II, and thus we refer to this as an “untilted” spectrum. The effect of finite f is to tilt or twist this spectrum one way or the other depending on the sign of f. The node adopts a positive slope when f > 0 and a negative slope when f < 0. Because the 2D-IR spectra contain both absorptive and dispersive contributions, this tilting is present in S̃_R(ω_τ, ω_t) and S̃_NR(ω_τ, ω_t) even for uncorrelated modes. Therefore an accurate determination of the frequency correlation requires fitting the data to theoretical simulations of the purely absorptive spectrum, S̃(ω_τ, ω_t), isolated by adding the complex rephasing and nonrephasing spectra after the procedure from NMR (24), which was applied recently to 2D-IR spectroscopy (5, 25, 26).

Results

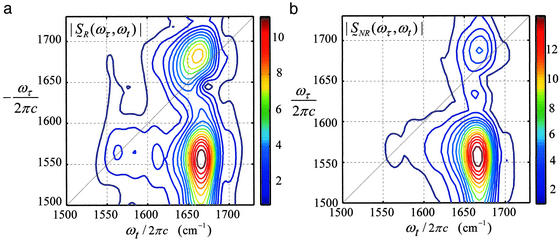
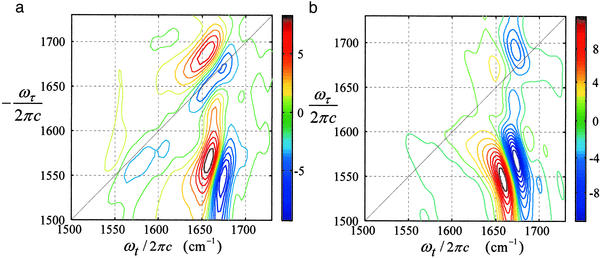
Dual-frequency 2D-IR absolute magnitude spectra |S̃_R(ω_τ, ω_t)| and |S̃_NR(ω_τ, ω_t)| corresponding to the rephasing and nonrephasing sequences are shown in Fig. 4. The cross peak caused by coupling of the amide I and amide II modes is much stronger than the diagonal peaks and is tilted slightly toward the antidiagonal direction. The amide I diagonal peak at 1,662 cm⁻¹ is stronger in the rephasing spectrum, which implies that the amide I band consists of an inhomogeneous distribution of frequencies that persists over the experimental time scale (5, 23, 27), again justifying the use of Bloch dynamics. Three separate measurements showed that the cross peak is 1.23 ± 0.05 times stronger in the nonrephasing spectrum. This ratio is sensitive to the correlation coefficient. For example, when the two vibrators are uncorrelated it is 1.0, whereas for negative f the ratio is always greater than unity. Therefore a negative correlation between the amide I and amide II frequency distributions is indicated.

Figure 4.

Absolute magnitude spectra of NMA in DMSO obtained for rephasing (a) and nonrephasing (b) dual-frequency 2D-IR spectroscopy. Symbols are as defined in Modeling the 2D-IR Spectra.

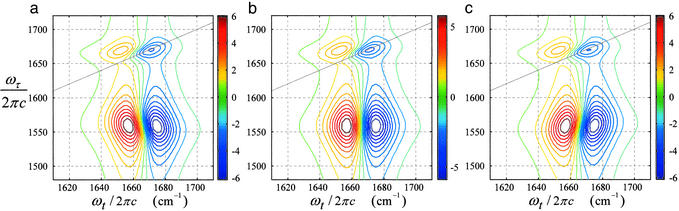
As expected, the real parts of the 2D-IR spectroscopy cross spectra in the nonrephasing and rephasing sequences exhibit tilted resonances (see Fig. 5). The absorptive spectra Re{S̃(ω_τ, ω_t)} modeled with different correlation factors are shown in Fig. 6. The tilt of both negative and positive peaks is very sensitive to the correlation factor and exists only when the frequencies of the vibrators are correlated (Fig. 6 a and c). It is the negative correlation that causes the tilt toward the antidiagonal direction of the absorptive spectra similar to the observations (Fig. 7a). The tilt angle is also affected by the width of the frequency distributions in each of the interacting modes. These inhomogeneous contributions to the line widths for both amide I and amide II transitions were acquired from the analysis of the diagonal peaks.

Figure 5.

Real part of 2D-IR spectra of NMA for rephasing (a) and nonrephasing (b) sequences.

Figure 6.

Absorptive dual-frequency 2D-IR spectra simulated to illustrate the effect of frequency correlations of the two vibrators included. The correlation factors are −1 (a), 0 (b), and +1 (c). The parameters for the vibrators are close to those of the amide I and amide II modes of NMA in DMSO.

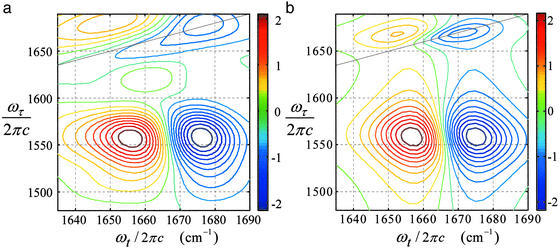
Figure 7.

Dual-frequency 2D-IR cross-peak spectra of NMA in DMSO: experiment (a) and simulated (b). The solid line is the diagonal of the 2D-IR spectrum (ω_τ = ω_t).

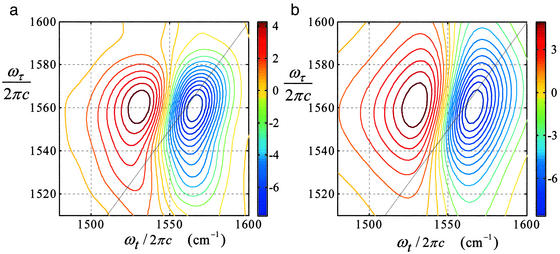
Diagonal Spectra.

The 2D-IR spectroscopy amide II diagonal spectrum is shown in Fig. 8 as the sum of rephasing and nonrephasing sequences. In this case the tilt angle of 0.26 ± 0.04 radians, defined as the angle between the ω_τ axis and the line parallel to the node in the real part of the 2D-IR spectrum in the region of ω_τ = ω_II, determines the inhomogeneous contribution to the line width. Simultaneous fitting of the absorptive 2D-IR spectroscopy, which yields the ratio σ_II/γ_II, and the linear spectra, which give a combination of the two parameters, allowed both σ_II and γ_II to be determined accurately. The modeling establishes σ_II/2πc = 11.2 cm⁻¹ and γ_II/2πc = 12.3 cm⁻¹, corresponding to a ratio of σ_II/γ_II = 0.91. The population relaxation time T₁ was determined experimentally to be 0.3 ps for the amide II mode, and thus the only adjustable parameters in this fitting procedure were the pure dephasing of amide II, determined to be 1.5 ps, and σ_II. A similar analysis for the amide I diagonal peak results in σ_I/2πc = 7.3 cm⁻¹ and γ_I/2πc = 4.0 cm⁻¹ giving a ratio of σ_I/γ_I = 1.8. These parameters are needed to interpret the cross-peak signals.

Figure 8.

The diagonal 2D-IR spectra in the amide II region of NMA in DMSO. The solid line is ω_τ = ω_t.

Cross Peaks in Dual-Frequency 2D-IR Spectra.

By using spectrally shaped laser pulses the cross-peak profile can be measured accurately, and the coupling and the correlations of the frequencies of the two vibrators can be determined. The correlations help to establish mechanisms for the coupling of modes, thus they add to the structural constraints. The correlations between the frequencies of one of the vibrators and the off-diagonal anharmonicity can readily be incorporated into the modeling (13), but no indication of such correlations was observed for the amide I/II modes of NMA.

The cross-peak features in the absorptive spectrum (Fig. 7a) are tilted in the antidiagonal direction by an angle of −0.045 ± 0.006 radians. A simulation of the dual-frequency 2D-IR spectroscopy cross peak (Fig. 7b) with the parameters for amide I and amide II transitions given above for the diagonal peaks gave a frequency correlation factor of f = −0.28 ± 0.06. The cross-peak tilt angle is more sensitive to the inhomogeneous contribution σ_II than that of σ_I. This is because the amide II band has a much smaller value of σ/γ, which results in a blurring of the frequency distribution by the larger homogeneous broadening.

Polarization Effects.

The ratio of the 2D-IR spectral amplitude at the isolated cross peak for parallel to that for perpendicular polarized fields at ω₁ and ω₂ was found to be 1.35 ± 0.1.

Discussion

The importance of 2D-IR spectroscopy as a structural and dynamical probe of peptides and other complex systems lies in its ability to simplify spectra and yield properties that are not available from linear spectra. However, the spectra are often diffuse and dominated by diagonal signals that obscure the interesting new information carried by the cross peaks, which may arise because of very small coupling constants. The present results show that by using dual frequencies the cross peaks can be isolated and studied independently of the diagonal peaks. Furthermore the method permits the measurements of coupling between modes that are separated in frequency by more than the bandwidth currently achievable by single laser pulses in the IR. For example measurement of the coupling of the N—H and C⩵O modes of peptides would require single-frequency pulses having a width of 9 fs centered between the two modes. However, the vibrational dynamics of the coupled modes is sufficiently slow that it can be measured with 250-fs pulses. Therefore the method of choice will be dual-frequency 2D-IR spectroscopy either by means of IR echoes, exemplified by the experiments described here, or the pump-probe 2D-IR spectroscopy methods described in our earlier work on N—H/C⩵O coupling (14).

Coupling Strength.

The coupling strength was determined from comparisons of the diagonal amide I mode signal and the dual-frequency cross peak. An off-diagonal anharmonicity of Δ_I,II/2πc = 3.5 ± 0.5 cm⁻¹ was obtained, clearly indicating a significant coupling between the two modes. This may seem to be a small effect, but it should be remembered that the observed signal, Eq. 1, is the difference between two large quantities that disappears if the modes are uncoupled when t < T. The existence of the coupling is confirmed by the observation of cross peaks and of the oscillations seen in the heterodyned transient-grating signal (data not shown). The experimental result stands in contrast to recent computations that have predicted the anharmonic coupling between the amide I and amide II modes in the same peptide unit to be zero (28). The coupling, β, between the I and II modes that is implied by the measured anharmonicity can be estimated in lowest order from a three-level model in which the I + II combination band couples to both the I and II overtones through a bilinear interaction β(ω_Iω_II/ℏ²)^1/2Q_IQ_II, where the Q values are the normal (harmonic) modes. This three-level model, the predictions of which are obtained by diagonalization of a three-by-three matrix in the basis of 2 × I, 2 × II, and I + II, predicts a value of 27 cm⁻¹ for β, which does not seem unreasonable for the interaction of two transition charge distributions spread over the same set of four peptide atoms.

Frequency Correlations.

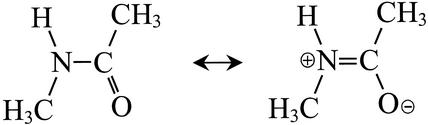
A negative correlation between amide I and amide II frequencies must be related to the bond-order changes induced by solvent and structural fluctuations. The two dominant valence-bond structures for the ground state of NMA are shown in Fig. 9. The N—C double-bond character of ≈40% (29) is responsible for the planarity of the peptide group. The interactions of NMA with DMSO in the different solvent configurations cause it to adopt a range of structures. Each structure is considered to correspond to a slightly different admixture of the dominant valence-bond functions. Those structures with more double-bond character of the carbonyl group will have less N—C double-bond character. The amide I band is mainly the C⩵O stretch motion, thus its frequency is reduced in structures with more N—C double-bond character. The amide II mode is significantly an N—C stretching motion, and thus its frequency would be increased accordingly. This provides an explanation as to why the frequencies in the distributions of the two modes are anticorrelated. The analysis provides an example of the power of 2D-IR spectroscopy in exposing the detailed content of structural distributions and has obvious applications in experiments with more complex peptides where structural distributions are functionally important.

Figure 9.

The dominant valence-bond structures of NMA.

Angular Properties.

The 2D-IR spectral amplitudes were measured for the fields at ω₁ and ω₂ having parallel and perpendicular polarizations. The ratio, P, of these two measurements according to Eq. 1 is 〈Z_IIZ_IZ_IIZ_I〉/〈Z_IIX_IZ_IIX_I〉, which is directly related to the alignment of the amide I and II transition dipoles (16, 23) through the relationship

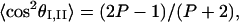where θ_I,II is the angle between the transition moments and the average, 〈 〉, is over the distribution of alignments found in the structure distribution. The two possible alignments obtained from the experimental ratio at the peaks of the distributions are 45 ± 5° and 135 ± 5°. Assuming the amide I transition dipole to be 20° from the C⩵O bond (13, 30) and the OCN angle to be ≈123° (29), the preferred direction of the amide II mode is 8 ± 5° to the N—C bond and 65 ± 5° to the C⩵O bond. The former value compares well with 12°, obtained recently for the amide II dipole alignment to the N—C bond in AcProNHMe (13), and the latter is close to the value of 73° reported earlier for this alignment (30).

Dual-Frequency Echoes.

Traditional pictures of photon or spin echoes often imply that the creation of the macroscopic signal requires rephasing to occur within the same inhomogeneous distribution that was involved in the coherence evolution after the first pulse (27, 31). We see here that what is important in obtaining an echo are the correlations between the distributions that are present during τ and t, which possibly may have quite different origins and may lose and regain macroscopic polarization on different time scales. So-called two-color echoes have been reported for electronic transitions by using visible laser pulses (32, 33).

Conclusions

Dual-frequency heterodyned 2D-IR spectra are obtained for NMA in DMSO. Tunable suppression of the diagonal peak contribution to 2D-IR spectroscopy is demonstrated up to complete elimination. Construction of 2D-IR spectra of the isolated cross peaks is shown to be a useful and convenient way to visualize and measure frequency correlations in 2D-IR spectroscopy. The amide I/amide II frequency correlation factor in NMA is determined to be −0.28 ± 0.06, consistent with solvent-induced structure fluctuations of the admixtures of principal valence-bond structures of the peptide bond. The coupling between amide I and II modes is estimated as 27 cm⁻¹ from a measured mixed-mode anharmonicity of 3.5 cm⁻¹.

Implementation of dual-frequency spectrally shaped coherent IR pulses to 2D-IR spectroscopy opens up new and exciting possible applications to biological macromolecules. Current laser technology can provide very large bandwidth IR pulses (200–300 cm⁻¹) having widely tunable center frequencies. These could be used in pairs in the manner described herein to access a broad range of the vibrational spectrum. A detailed picture of the evolution of the anharmonic nature of the potential surfaces of macromolecules will be obtainable while structural changes are taking place. The two frequencies could be chosen to access different modes of a peptide structure or two modes belonging to different types of molecules such as a protein and a nucleic acid, a protein mode and solvent, or a protein tertiary interaction. Sequences of five IR pulses can also be envisaged (21) that will be able to expose even more complex spatial relationships.

Abbreviation

NMA

N-methylacetamide