Scaling behavior of random knots

Abstract

Using numerical simulations we investigate how overall dimensions of random knots scale with their length. We demonstrate that when closed non-self-avoiding random trajectories are divided into groups consisting of individual knot types, then each such group shows the scaling exponent of ≈0.588 that is typical for self-avoiding walks. However, when all generated knots are grouped together, their scaling exponent becomes equal to 0.5 (as in non-self-avoiding random walks). We explain here this apparent paradox. We introduce the notion of the equilibrium length of individual types of knots and show its correlation with the length of ideal geometric representations of knots. We also demonstrate that overall dimensions of random knots with a given chain length follow the same order as dimensions of ideal geometric representations of knots.

Many theoretical and experimental studies are devoted to understanding how overall dimensions of random walks change with their number of steps (1, 2). This question is interesting from theoretical and practical point of views, because polymers at thermodynamic equilibrium behave like random walks of two principal types. Polymer chains suspended in a good solvent and thus showing repulsive intersegmental interactions follow rules of self-avoiding random walks. In these walks their segments do not approach each other closer than a certain distance that reflects the effective diameter of the polymer under given conditions. It was experimentally observed and theoretically predicted that overall dimensions of self-avoiding random walks scale with the number of segments N as N^ν, where ν ≈ 0.588 (3). Qualitatively different behavior was observed for polymers suspended in so-called theta solvents where on large length scale independent segments behave as neither repulsing nor attracting each other and for polymers in dense melt phase where individual chains are intermingled with many other chains. Under these conditions the scaling exponent ν = 0.5, and polymers follow the behavior of ideal random walks. This latter type of walk can be modeled as chains of freely jointed segments of equal length having no thickness and in which each segment in the modeled chain corresponds to one Kuhn statistical segment in a polymer (2, 4). More recently there has been an increased interest in the scaling behavior of polymers with closed trajectory forming trivial or nontrivial knots (5–9). Simulation studies of unknotted circular chains suggested that for very long chains their scaling exponent ν approaches 0.588 even in the absence of intersegmental repulsion (7). Theoretical studies conjectured that in long-chain regime polymers with effective diameter zero but forming any fixed type of knot, the scaling exponent is 0.588 (8). The same studies also proposed that more-complex knots would need a longer chain length to reach the scaling exponent of 0.588 (8). In contrast to earlier work, we demonstrate here that even in the relatively short chain-length regime random walks with no exclusion volume behave as self-avoiding walks (ν ≈ 0.588) when the walks of increasing length are divided into groups consisting of individual knot types. It may seem paradoxical that each topological subset of random walks shows the scaling exponent of 0.588, but when all different knots are grouped together, their average scaling exponent ν = 0.5. We explain here this apparent paradox.

Chains with Nonfixed and Fixed Topology

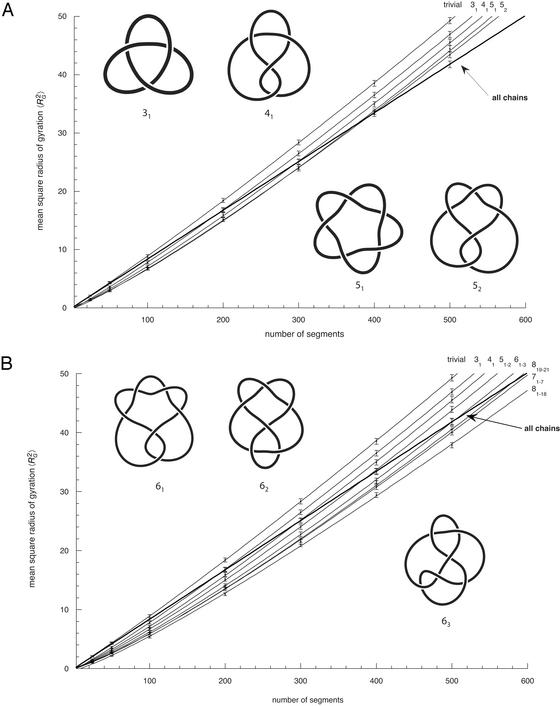
For the generation of closed trajectories we used an approach in which the closed random walks are produced from random sets of equal-length vectors having a total sum of zero (10, 11). The generated trajectories had no thickness. Knot types of generated chains were recognized by calculation of their HOMFLY polynomials (12, 13). Our data are based on statistical samples consisting of at least 10⁵ configurations at each analyzed chain length of closed random walks. The analyzed sizes ranged from 24 to 500 segments. Overall dimensions of polymers are usually characterized by their radius of gyration (R_G), which is equal to the root-mean-square distance from the center of the mass of the chain. The R_G can be calculated easily for each simulated configuration (14). Fig. 1A shows relations between the mean-square radius of gyration (〈R〉) and the number of segments for all closed random walks of a given length (thick line) and for statistical samples consisting of individual knot types (trivial, 3₁, 4₁, 5₁, and 5₂) of a given length. When all closed walks are grouped together, one observes a linear relation between their 〈R〉 and N values. One can therefore simply apply the relation 〈R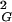〉 ∝ N^2ν and thus see directly that the exponent ν = 0.5. The observed slope is 1/12. This result was theoretically predicted, because for linear random chains 〈R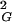〉 = 1/6 NL, where N is the number of segments and L is the length of segments (14), whereas for circular random chains the values of 〈R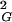〉 are simply half as large as those for linear chains (8). The strong agreement between analytical results and our simulation data obtained for all closed walks grouped together positively confirms our simulation and calculation procedure. Fig. 1A shows also that values of 〈R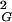〉 for individual knot types have higher growth rates than corresponding values for all closed walks. Trivial knots and other analyzed knot types seem to behave thus as walks with excluded volume as it was theoretically proposed before (8). Self-avoiding behavior was earlier demonstrated numerically for trivial knots (7), whereas studies of other knots only permitted to tell that their individual scaling exponents were >0.5 and <0.6 (9). In self-avoiding random walks the relation 〈R〉 ∝ N^2ν is only valid for very long chains. These cannot be analyzed efficiently by computer simulation, and therefore in practice one cannot use this relation to determine the ν exponent (6). However, the asymptotic behavior of the ν exponent allows us to fit our numerical data, obtained for chains with up to 500 segments, using a more complex formula,

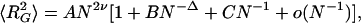1

where A, B, C, and ν are free parameters and Δ is set to 0.5 (6). To determine the growth rate and thus the ν exponent for individual knot types we collected 〈R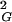〉 values of individual knot types at different chain lengths and fitted these data using Formula 1 while leaving the parameters A, B, C, and ν as free. We limited our analysis in Fig. 1A to knots with up to five crossings, because our statistical samples were sufficiently robust for these knots. In all analyzed cases, the scaling exponent ν, which was left as a free parameter of the fit, converged to a value close to 0.588. We observed, however, a slight scatter of ν values for different knots. This scatter probably was due to a limited statistical sample and to allowing too many free parameters in the applied fit. It therefore was important to limit the number of free parameters. Orlandini et al. (6) suggested that the amplitude value in Formula 1 should be independent of the knot type. We therefore fixed the amplitude (A) to a value of 0.02685, which was the mean value obtained in independent fits for different knot types, and then repeated the fitting procedure leaving the parameters B, C, and ν as free. This second fitting resulted in very narrow distribution of the ν exponent around the value of 0.588 (see legend to Fig. 1A), which for knots with the biggest statistical samples (trivial and 3₁) practically coincided with 0.588. Our data show therefore that even relatively short closed walks of a given knot type behave as self-avoiding walks despite the fact that the effective diameter of the simulated chains was set to zero.

Figure 1.

Scaling of 〈R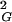〉 of random non-self-avoiding random knots with respect to the chain length. The scaling profile for all closed walks grouped together is drawn with the thicker lines, and it clearly follows a linear relation pointing to a scaling exponent of 0.5, whereas scaling profiles of individual knot types (A) or group of knots (B) show higher growth rates characteristic for self-avoiding walks. (A) Scaling profiles of individual knot types were obtained by fitting experimental points with Formula 1, leaving parameters A, B, C, and ν as free. The best-fit values for the scaling exponent ν obtained for trivial knots (unknots), trefoils (3₁), figure-of-eight knots (4₁), and 5₁ and 5₂ knots were 0.589, 0.590, 0.594, 0.596, and 0.590, respectively. The nomenclature of knots follows this in standard tables of knots where the main number indicates the minimal number of crossings of a given knot and the subscript number indicates the knot tabular position among the knots with the same number of crossings (25, 26). (B) Scaling profiles of individual knot types or of a group of knots are here fitted to experimental points by using Formula 1, leaving parameters B and C as free but imposing the scaling exponent ν of 0.588 in each case. The quality of the fit was better than 0.9998 in each case. The error bars denote standard deviations.

One may wonder how is it possible that random walks of any given knot type show the scaling exponent of 0.588, whereas all knots taken together show the scaling exponent of 0.5. To answer this apparent paradox one should look carefully at the scaling behavior of more knots. In Fig. 1B we present the scaling exponent of knots with up to 8 crossings. To have a sufficiently big statistical sample (and thus small statistical error) we have grouped together the 2 different knot types with five crossings, 3 different knot types with six crossings, 7 with seven crossings, 18 alternating knot types with eight crossings, and 3 nonalternating with eight crossings. Although random walks forming these different groups of knots seem to show the same scaling exponent, the actual profiles of their scaling behavior are substantially different. Simple knots quickly reach higher 〈R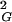〉 values than the global average of 〈R〉 observed for a given size of all generated closed walks. 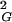More-complex knots require longer lengths to reach higher 〈R〉 values than the global average of 〈R〉 observed for a given size of all generated closed walks. With increasing chain length one observes progressive formation of more-complex knots (15). Therefore, for any sufficiently large chain length, there are always complex knots with their 〈R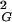〉 values smaller than the global average of 〈R〉, and there are also simpler knots that have their 〈R〉 values bigger than the global average of 〈R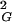〉. The weighted average over all types of observed knots (weighted according to their relative probabilities of occurrence at a given chain size) results then in the global average of 〈R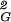〉. Thus it is possible to have all topological subsets of walks to show the scaling exponent of 0.588, when taken separately, and observe the scaling exponent of 0.5 when all subsets of walks are taken together. Grosberg (8) proposed a similar explanation for the discrepancy between the scaling exponent of individual knots and all closed walks grouped together, but he did not know the actual scaling profiles for different random knots.

Equilibrium Length of Knots

One should also discuss why random walks forming a given knot type are initially more compact than the average size of all walks of a given length, and then as their length increases they become less compact than the average size of all walks with the same length. This behavior of random knots is easy to understand. Knotted random chains have smaller overall dimensions as compared with unknotted chains. The more complex the knot, the smaller their overall size among random knots of the same chain length. At the same time lengths of walks required to form more-complex knots are longer than those required to form simpler knots. Therefore, when knots of a given type (with exception of trivial knot) first start to appear among random walks of the same length, they are in the overwhelming company of less-complex knots with bigger overall dimensions. As the analyzed length of random walks increases one can see the progressive appearance of more-complex knots. At some critical length each individual knot type becomes dominated by more-complex knots of the same length. Starting from this length, this knot should have its average overall dimensions bigger than average dimensions of all closed walks with this chain length. Fig. 1 shows that the scaling profiles of different knots intersect with the global scaling profile of all closed walks at different chain lengths. At these points of intersection random walks of a given knot type (or category, e.g., knots with six crossings) have their mean size equal to the global mean size of all closed random walks with this chain length. We will call this length the equilibrium length of a given type of knot (or a category of knots). The concept of equilibrium length of knotted polymers can be illustrated by a hypothetical example of cleavage and recircularization reaction acting on a given type of polymer. When, for example, short DNA molecules forming trefoil knots are cut with a restriction enzyme that cleaves each molecule once and are then reclosed by using an enzyme ligase, one should observe that the majority of the molecules increases their R value and gets converted into unknots. In contrast, when very long DNA molecules forming trefoil knots are linearized and then reclosed by ligase, one should observe that the majority of the molecules decreases their R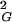 value and forms knots that are significantly more complex than trefoils. At the equilibrium length the situation is different; 〈R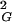〉 does not change after cutting and religation, and a significant fraction of the molecules will reform trefoil knots. The equilibrium length of a given knot type formed by a polymer in solution depends on the solvent conditions. In a good solvent this length will be bigger than in a poor solvent. In theta solvents one will get the intermediate value. Using ideal random-walk simulations we analyze the situation corresponding to polymers suspended in theta solvents. The values of equilibrium lengths of different knots are expressed in the number of statistical segments of a given polymer. In the case of double-stranded DNA, one statistical segment has a length of ≈100 nm (16). However, depending on the relative stiffness of the polymer, the metric length of the statistical segment changes. The equilibrium lengths of different knot types in theta solvent can be obtained relatively easily by simulations of random walks and constitute interesting characteristics of a different knot type. The equilibrium length is intrinsic for a given knot and is not affected by the interplay between different knots, as is the case of the length at which a given knot type shows its highest occurrence among all other knots with the same length (11, 17–19). The equilibrium length is determined simply by the intersection of the actual scaling profile of R 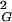of a given knot with the analytically derived linear-scaling function of 〈R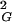〉 of all knots.

Random Knots and Ideal Knots

We observed earlier that ideal geometric representations of knots, defined as the shortest possible trajectories of cylindrical tubes forming a given knot type, show interesting relations with several different characteristic values of random knots of a given type (20–23). For this reason we compared the length of ideal knots, the length/diameter value obtained for a shortest possible trajectory of a cylindrical tube forming a given knot, with the equilibrium length of the corresponding knots. Fig. 2 shows the relation between the equilibrium length of random knots of a given type (or group of knots) and the length of corresponding ideal knots. The ordering of knots, according to their equilibrium length, seems to be the same as their ordering according to the length of ideal configuration. In addition we observe a power-law function dependence between the length of ideal knots and the equilibrium length of corresponding knots. More data are needed to demonstrate that this relation also holds for more-complex knots. Fig. 1 shows that not only equilibrium lengths but also overall dimensions of different knots of a given length follow the same order as the one observed in ideal knots. For a fixed length of ideal knots, the overall dimensions decrease with increasing length/diameter ratio of ideal knots (20). We therefore investigated the relation between differences in 〈R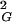〉 between unknot and a given knot with the same chain length and the length/diameter ratio of a corresponding ideal knot. Fig. 3 shows these relations for random knots composed of 100 and 500 segments. These plots are normalized by setting the difference between 〈R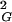〉 of unknots and trefoils to 1 for both analyzed chain lengths. In both cases (100 and 500 segments) the observed relations seem to follow simple power-law functions, where the actual values of the fit change with the analyzed chain length.

Figure 2.

Correlation between equilibrium length of different knots and the length of ideal geometric representations of the corresponding knots. Because the statistical sets of individual complex knot types obtained in our simulations were not numerous enough, we grouped together two knot types with five crossings knots, because these have similar length of their ideal configurations. For the same reason we put three knots with six crossings into one group and seven knots with seven crossings into another group. The knots with eight crossings were divided into two groups, alternating (8₁–8₁₈) and nonalternating (8₁₉–8₂₁), because these two groups significantly differ in the length of their ideal configurations (27).

Figure 3.

Correlation between differences in 〈R〉 of trivial knots and knots of a given type (or a group of knots) and the lengths of ideal geometric representations of the corresponding knots. Plots are normalized by setting to 1 the difference in 〈R〉 of trivial knots and trefoil knots with the same chain size. The two normalized profiles correspond to random knots with 100 and 500 segments.

Summary

We have shown here by numerical simulations that when non-self-avoiding random knots are divided into individual knot types, the scaling behavior of each individual knot type is the same as that of self-avoiding walks. Almost paradoxically each knot type therefore shows the same scaling exponent ν of ≈0.588, whereas when all knotted walks are grouped together the scaling exponent ν of 0.5. We have explained this apparent paradox, but our explanation should not stop us from wondering why the relative probabilities of different knots are all tuned in such a way as to give the global scaling exponent ν of 0.5 out of individual scaling exponents ν of 0.588. We also demonstrated that equilibrium lengths and overall dimensions of random knots of different types follow the same order as observed in ideal geometric representations of knots. Our study of the natural spectrum of knots shows that the character of this spectrum follows that predicted by using simple geometric criteria or general energetic considerations (20, 24).