Abstract
Within a large-scale neuronal network model of macaque primary visual cortex, we examined how intrinsic dynamic fluctuations in synaptic currents modify the effect of strong recurrent excitation on orientation selectivity. Previously, we showed that, using a strong network inhibition countered by feedforward and recurrent excitation, the cortical model reproduced many observed properties of simple and complex cells. However, that network’s complex cells were poorly selective for orientation, and increasing cortical self-excitation led to network instabilities and unrealistically high firing rates. Here, we show that a sparsity of connections in the network produces large, intrinsic fluctuations in the cortico-cortical conductances that can stabilize the network and that there is a critical level of fluctuations (controllable by sparsity) that allows strong cortical gain and the emergence of orientation-selective complex cells. The resultant sparse network also shows near contrast invariance in its selectivity and, in agreement with recent experiments, has extracellular tuning properties that are similar in pinwheel center and iso-orientation regions, whereas intracellular conductances show positional dependencies. Varying the strength of synaptic fluctuations by adjusting the sparsity of network connectivity, we identified a transition between the dynamics of bistability and without bistability. In a network with strong recurrent excitation, this transition is characterized by a near hysteretic behavior and a rapid rise of network firing rates as the synaptic drive or stimulus input is increased. We discuss the connection between this transition and orientation selectivity in our model of primary visual cortex.
Keywords: hypercolumns, numerical simulation, V1, circular variance
Orientation selectivity and spatial summation (1) are two fundamental attributes of visual processing performed by the mammalian primary visual cortex (V1). V1 is the first cortical area along the visual pathway where neurons are strongly selective for stimulus orientation. Moreover, measurements of orientation selectivity for individual neurons, such as the tuning curve bandwidth (half-width at half maximum), circular variance (CV),¶ and orientation selectivity index, often show near independence of stimulus contrast. V1 neurons are also classified as either “simple” or “complex” based on their spatial summation properties. Simple cells respond to visual stimulation in an approximately linear fashion, whereas complex cells respond more nonlinearly. For example, when driven by drifting sinusoidal gratings, a simple cell follows the temporal modulation of the drifting grating as the grating moves across the receptive field of the neuron, whereas complex cells show an elevated but unmodulated response. Quantitatively, simple and complex cellular responses are often differentiated by the modulation ratio F1/F0 (at preferred stimulus orientation, the ratio of the first Fourier component and the mean) of the cycle-averaged firing rate (2): cells with F1/F0 > 1/2 are simple and cells with F1/F0 < 1/2 are complex.
How orientation selectivity arises in V1 has not been fully elucidated (3, 4). According to the classical Hubel and Wiesel picture (5), orientation selectivity arises directly from the convergence of lateral geniculate nucleus (LGN) afferents. However, modeling based on the Hubel and Wiesel, or “feedforward,” picture shows that the degree of selectivity provided by the convergent LGN inputs alone is insufficient to explain extant data (3). Some form of cortical processing seems necessary.
V1 responses have been investigated through a variety of models of differing architectures and coupling schemes. Modifications of the feedforward scheme have used Hebbian ideas to posit cortical circuitry with highly specific cortical inhibition. The push–pull model (6) is an example of such a modification: intracortical inhibition is anticorrelated with the excitatory synaptic drive. Other models without highly feature-specific coupling demonstrate that selectivity can arise from the sharpening of weakly tuned feedforward excitation by broadly tuned intracortical inhibition (see, e.g., refs. 7–9). The so-called marginal phase, which can evince contrast invariance, arises when cortical excitation is sufficiently strong to allow symmetry-breaking states (10).
Previously, we studied how simple and complex cell responses arise in a large-scale neuronal network model of an input layer 4Cα of macaque V1 (11–13). The model represents a 1-mm2 local patch with four orientation hypercolumns containing O(104) conductance-based, integrate-and-fire (I&F) neurons: 75% excitatory and 25% inhibitory. The cortical architecture, the LGN drive, and the cortico-cortical synaptic couplings are constrained whenever possible by anatomical and physiological measurements. In this large-scale model, a continuum of simple and complex cellular responses arises from the varying trade-offs between cortico-cortical and geniculate excitation: the most simple of the model neurons are driven strongly by the LGN and are “linearized” by strong cortical inhibition (12). In its published form, this model operated in a regime where its membrane conductances and potential had large fluctuations over its mean (see figures 4 and 5 of ref. 13). Indeed, it was these fluctuations that drove the network activity because the trial-averaged membrane potential was below the firing threshold,‖ as has also been observed experimentally (14). The origin of these fluctuations, which helped stabilize the network responses, was in large part external through the inclusion of membrane conductances (in addition to the cortico-cortical ones) driven by stimulus-independent Poisson spike trains. This particular model, while reproducing many aspects of simple and complex cell behavior, has complex cells that are only weakly selective for orientation. The strong cortical amplification that is apparently necessary to improve the orientation selectivity of complex cells causes bistability: complex cells tend to either not fire at all or to be mean-driven, with firing rates that are much too high (limited only by the absolute refractory period). This bistability occurs despite the presence of noisy external conductances.
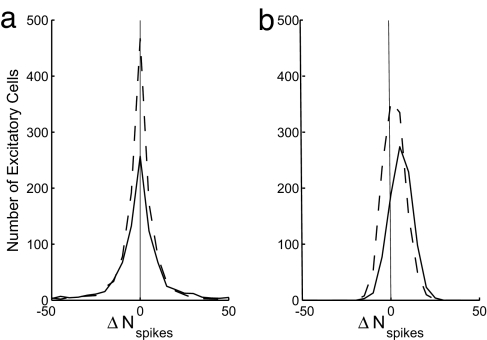
Fig. 4.
Hysteresis in the V1 model. Shown is the distribution in ΔNspike (the difference in the number of spikes during stimulus contrast decrement and increment; see text) for the ES (dashed lines) and EC (solid lines) populations. (a) Neff = 96 (p = 0.02344). (b) Neff = 768 (p = 0.1875). All other model parameters are the same as in Fig. 1. The complex cells of the densely coupled, Neff = 768 network show evidence of hysteresis in stimulus contrast. The stimulus contrast was increased linearly in time from 0% (at t = 0) to 100% (t = 5 s) and then decreased linearly in time from 100% to 0% (ending at t = 10 s).
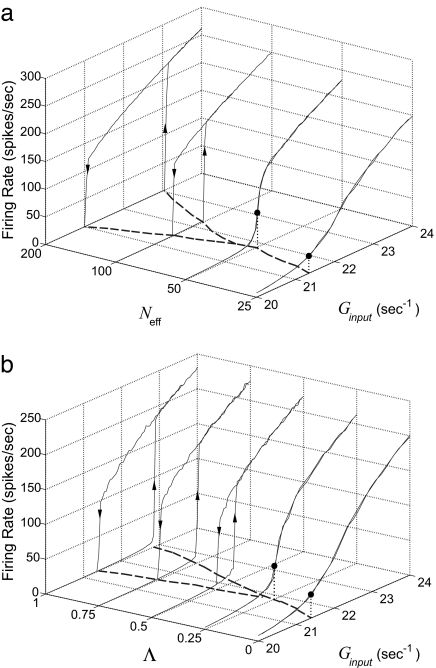
Fig. 5.
Bifurcation diagrams. Shown is the firing rate per neuron of the EC population vs. Ginput. These curves were obtained by first increasing and then decreasing the strength of the feedforward excitation Ginput for our idealized networks with different Neff = 25, 50, 100, and 200 [the network synaptic coupling strengths are SEE(s) and SIE(s) = 0.25 for the simple cell population; SEE(c) and SIE(c) = 0.5 for the complex cell population; and SEI = SII = 0.9 for all cells; Λ = 0.0 for each of the models shown] (a) and for five idealized networks with different Λ = 0%, 25%, 50%, 75%, and 100% (the network synaptic coupling strengths are the same as in a, with Neff = 25 for each model shown) (b). The dashed curves on the plane Neff − Ginput correspond to 〈VS(Neff,Ginput)〉 = VT for EC cells, where 〈VS〉 ≡ [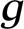 LVR + (SEE(s)mEs + SEE(c)mEc)VE + (SEImIs + SEImIc)VI]/[
LVR + (SEE(s)mEs + SEE(c)mEc)VE + (SEImIs + SEImIc)VI]/[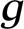 L + (SEE(s)mEs + SEE(c)mEc) + (SEImIs + SEImIc)], where mEs, mEc, mIs, and mIc are the firing rate of the simple and the complex excitatory and inhibitory cells, respectively. In the bistable region, there are two 〈VS〉 = VT curves, one corresponding to ramping-up the input Ginput and the other corresponding to ramping-down the input. The region of Ginput above the curves 〈VS〉 = VT corresponds to 〈VS〉 > VT. In the mono-stable region, the black dots mark the firing rate at 〈VS〉 = VT as indicated by the vertical projection (dotted line).
L + (SEE(s)mEs + SEE(c)mEc) + (SEImIs + SEImIc)], where mEs, mEc, mIs, and mIc are the firing rate of the simple and the complex excitatory and inhibitory cells, respectively. In the bistable region, there are two 〈VS〉 = VT curves, one corresponding to ramping-up the input Ginput and the other corresponding to ramping-down the input. The region of Ginput above the curves 〈VS〉 = VT corresponds to 〈VS〉 > VT. In the mono-stable region, the black dots mark the firing rate at 〈VS〉 = VT as indicated by the vertical projection (dotted line).
In ref. 15, we suggested that strong, intrinsically generated cortical fluctuations can stabilize network dynamics and allow complex cell selectivity. Here, we demonstrate how a critical level of strong synaptic fluctuations induced by sparsity in network connectivity can transform potentially destabilizing recurrent network amplification to stable and rapid gain through a near-bistability to produce orientation-selective complex cells. In all cells, the strong dynamic synaptic fluctuations provide the intrinsic “noise” to yield near contrast invariance. We examine the role of V1 architecture on orientation selectivity and show that, although extracellular selectivity for orientation is roughly independent of cortical location, intracellular measures are not, differing between neurons in iso-orientation regions and those near pinwheel centers, consistent with recent experiments (16). Finally, the role of synaptic fluctuations is elucidated in detail by studying the bifurcation structure of network activity in an idealized network model with statistically homogeneous coupling.
Results
Orientation Selectivity in a Large-Scale Model of V1.
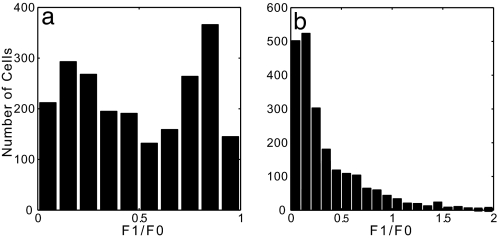
In this work, we concentrate on responses of our V1 model (see Methods) to drifting grating stimuli. Although typically used to measure orientation selectivity, drifting grating stimuli are often used to assay linearity in cellular responses. Fig. 1a shows the histogram of modulation ratio F1/F0 (from cycle-averaged time traces of extracellular spiking) for excitatory cells in the model. In qualitative agreement with experimental observation and with our previous model (13), we find a broad but bimodal distribution of modulation ratio, with many cells sitting astride the simple/complex divide, and with a characteristic depression around F1/F0 = 1/2 (17, 18). Fig. 1b shows an intracellular antecedent, the F1/F0 distribution of the intracellular effective reversal potential VS. Again, in agreement with experimental observation (19) and our previous model (13), this distribution is plainly unimodal, which in the model reflects the egalitarian nature of the basic connectivity (see also ref. 20).
Fig. 1.
Histograms of the modulation ratio, F1/F0, for excitatory cells in the model network; only cells with firing rate at peak angle above 5 spikes per sec are included. (a) Modulation ratio for the firing rate. (b) Modulation ratio for the intracellular voltage as measured by the effective reversal potential VS. The modulation ratio is measured from each cell’s cycle-averaged response to a drifting grating stimulus at high contrast and at preferred orientation. The synaptic coupling parameters are SEE = 0.25, SIE = 6.0 for the simple cells; SEE = 4.0, SIE = 7.0 for the complex cells; and SEI = SII = 2.0 for all cells. The effective network size is Neff = 96 (with NE = 72 and NI = 24), and the NMDA percentage Λ = 0.25.
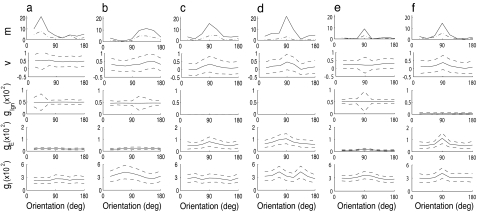
Orientation selectivity is typically measured by using time-averaged firing rates as a function of stimulus orientation, that is, from orientation tuning curves. In the large-scale model here, both simple and complex cells show a range of orientation selective responses, as does V1 cortex (17). Fig. 2a–d shows the tuning properties of four sample excitatory neurons near pinwheel centers**: two excitatory simple (ES) cells (Fig. 2 a and b) and two excitatory complex (EC) cells (Fig. 2 c and d). Fig. 2 e and f shows tuning properties for an ES (Fig. 2e) and an EC cell (Fig. 2f) in an iso-orientation domain (far from the pinwheel center). The simple cells are strongly driven by the LGN, whereas the complex cells are not. These cells have tuning curves that are roughly contrast invariant: their CVs are nearly equal at medium and low contrasts (Top, solid and dot-dashed lines, respectively). The remainder of the panels show intracellular potentials and synaptic conductances for a medium contrast stimulus as a function of the stimulus angle [temporal mean ± 1 SD; the temporal mean of the LGN input is untuned for orientation (3, 6)].
Fig. 2.
Tuning properties for cells (a–d) near the pinwheel center vs. cells (e–f) from iso-orientation domains. For six sample excitatory cells from the V1 model, plotted as functions of stimulus orientation within the five panels for each cell are (from Top to Bottom): firing rates (spikes per second) for medium contrast (solid lines) and low contrast (dot-dashed lines) stimuli; membrane potential; excitatory conductances from geniculate inputs; cortico-cortical excitatory conductances; and cortico-cortical inhibitory conductances. (Conductances are measured in units of inverse seconds.) All quantities are time-averaged, with the dashed curves showing the mean ± 1 SD. For the geniculate excitation, this standard deviation illustrates the tuning of its F1 component. With the exception of the topmost panels, all are at medium contrast. (a, b, and e) Simple. (c, d, and f) Complex.
Near pinwheel centers, the cortical conductances come from a population of cells with broadly distributed preferred orientations. In our previous models (11, 13), which were densely coupled, this scheme led to cortical conductances that were very nearly independent of stimulus orientation. One consequence was that simple cells were especially selective near pinwheel centers because of the interaction of excitatory conductances dominated by tuned geniculate input (that is, tuned in its non-mean components) with a cortical inhibition that was independent of orientation. The inputs to complex cells there, on the other hand, were dominated by untuned cortico-cortical conductances, both excitatory and inhibitory, leaving the complex cells themselves untuned. As Fig. 2 shows, sparsity of coupling much reduces these effects, and the cortical conductances near pinwheel centers now show mostly broad modulation with stimulus angle. The nature of this modulation can be highly variable. One simple cell (Fig. 2a) has cortical conductances that are mostly flat with orientation, whereas the other (Fig. 2b) has a broadly modulated cortical excitation that is in phase with the F1 component of the LGN drive (and the tuning curve), while the cortical inhibition is out of phase. For both complex cells, the inhibition has a complicated modulation, especially as inhibitory conductances sample over relatively fewer input cells than excitation. For the cell in Fig. 2d, there is a strong misalignment between the peaks of the total conductance (dominated by inhibition) and the peak of the tuning curve. Recent intracellular measurements of cells near pinwheel centers have also shown misalignments (16) of firing and conductance peaks. In general, the effect of the haphazard, sparser coupling in our model is to improve the tuning of complex cells near pinwheel centers (13) while reducing the relatively better tuning of simple cells near pinwheel centers seen in ref. 11.
Moving from pinwheel centers into iso-orientation domains, the synaptic coupling is increasingly between cells of nearly the same preferred orientation. If the cells there are highly selective to orientation, then necessarily the cortical conductances will also be highly selective, and complex cells will become selective as their tuned excitatory conductances overcome tuned inhibitory conductances. As Fig. 2 e and f illustrates, the cortical conductances are well tuned, most certainly in comparison with near pinwheel neurons. This network is well tuned in iso-orientation domains because of a reciprocal feedback loop between the simple cells, which receive geniculate excitation (tuned in its F1 component), and the complex cells, which are operating in a network state of near-criticality. This state of near-criticality will be illustrated shortly in a reduced model but is marked by a steep but stable gain curve for the complex cells made possible by the sparse coupling of the network, and is the basis for their good selectivity. The selectivity in the complex cell network also feeds back to the simple cells, thereby further improving their selectivity with respect to the feedforward case.
Note that, in each sample neuron, the time-averaged intracellular potential is well below threshold (i.e., the neurons are fluctuation-driven). This behavior is generally true of neurons in the model network. Therefore, it is the intrinsically produced, temporal fluctuations,†† here induced by the sparse network coupling, that drive neuronal firing and network activity. In contrast to external noisy synaptic input, where the fluctuation strength is independent of the network dynamics, sparsity-induced intrinsic fluctuations can dynamically adjust their strength in response to the overall network dynamics. In particular, these sparsity-induced fluctuations remove a bistability that is otherwise present in a densely coupled network and allow the network to operate in a stable high gain regime to produce well tuned complex cells.
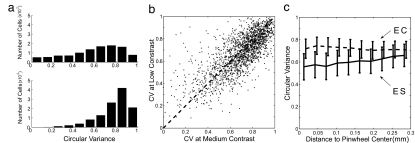
Fig. 3 summarizes the tuning properties of the excitatory neurons in this model. Fig. 3a shows the distribution of CV for the ES and the EC populations separately. Both populations are broadly distributed in CV, having ES cells somewhat better tuned than EC cells, in qualitative agreement with experimental data (17). Fig. 3b indicates that the orientation selectivity of the populations is approximately contrast invariant: the CV at medium stimulus contrast is on average equal to the CV at low stimulus contrast, with the data showing a large scatter (consistent with the experimental measurements‡‡). As already discussed, a distinct feature of previous versions (13) of this large-scale model was the clear differences in orientation selectivity relative to cortical location. As seen in Fig. 3c, there are differences in selectivity near and far from pinwheel centers, but they are slight. This roughly invariant selectivity in extracellular spiking across the cortical surface is in agreement with experimental measurements (16, 22, 23), as are the differences in tuning of cortical conductances near (broadly tuned) and far (more narrowly tuned) in cortical conductances (16, 23).
Fig. 3.
Orientation selectivity of excitatory cells in V1 model. (a) Histogram of CV for ES cells (Upper) and EC cells (Lower). (b) CV of excitatory cells at medium and low contrasts. (c) CV of excitatory population as a function of distance to nearest pinwheel center. Solid, ES; dashed, EC.
In producing these model results, large regions of the synaptic coupling strength parameter space were explored. We find that, to have roughly contrast invariant, selective complex cells, there must be strong recurrent excitation (13), with large intrinsic temporal fluctuations (15). To understand the effect of intrinsic synaptic fluctuations on network dynamics, we systematically varied the network sparsity through varying the connection probability p, thus varying Neff (see Methods).
We find that, without sufficient intrinsic synaptic fluctuation, the complex cells tend to be bistable in the presence of the strong recurrent excitation needed for amplification and orientation tuning, with the bistability leading to network properties that are biologically unrealistic, such as only a very few extremely well tuned complex cells with absolute-refractory-limited high firing rate, whereas the rest of the complex cells remain unresponsive. This behavior is illustrated by comparing model networks with differing Neff. Fixing the stimulus orientation, the stimulus contrast was slowly increased from zero to 100% contrast and then decreased back down to zero. For each cell, the number of spikes produced during the period of contrast increase was recorded, as were the number of spikes produced during contrast decrease. Let ΔNspikes denote the difference in the two, so that positive ΔNspikes means that the cell spiked more during contrast decrease than during contrast increase. Fig. 4 shows, for two networks with different Neff, the distributions of ΔNspikes of the ES and the EC populations. For the sparsely coupled, fluctuation-driven network [Fig. 4a; Neff = 96 with NE = 72 and NI = 24 (24, 25)], the distribution of ΔNspike is symmetric about 0, revealing no difference in the system response to contrast increment or decrement. However, in the (mean-driven) network with larger Neff (Fig. 4b; Neff = 768 with NE = 576 and NI = 192), the distribution of ΔNspikes for the EC population is skewed; that is, the EC cells are firing more during contrast decrement. This behavior is symptomatic of a hysteretic system. Note that this hysteresis increases as Neff is further increased (data not shown). To isolate and understand the effect of intrinsic fluctuations, we turn next to an idealized, statistically homogeneously coupled model and examine how synaptic fluctuations transform the input–output relation of strongly recurrent networks.
Fluctuation-Controlled Criticality.
We now consider a reduced, very idealized model network wherein 50% of the neurons receive feedforward drive (mimicking simple cells), 50% receive strong intracortical excitation (mimicking complex cells), and the coupling is statistically homogeneous (see Methods). Both populations receive the same, strong, cortico-cortical inhibition, i.e., SEI = SII being relatively large. We focus on the effect of fluctuations by ignoring detailed time dependencies of the visual drive; all simple cells receive the same feedforward drive of mean Ginput = ƒν0. For networks with the same network synaptic coupling strengths but of different Neff (i.e., the average coupling strengths remain the same as Neff is varied), Fig. 5a displays the complex cell population firing rate as a function of the mean drive Ginput. These firing rate curves are obtained by first increasing and then decreasing the feedforward input. In the Neff = 200 network, hysteresis is observed as we ramp up and then down the strength of the feedforward drive. This behavior is well captured by the solution of our kinetic theory analysis (data not shown) (15). The transition is a saddle-node bifurcation in Ginput for the mean population firing rate. As Neff is decreased (while strengthening individual synapses to keep the effective network drive constant), the region of bistable behavior in Ginput becomes smaller and smaller, until the bistability disappears completely and a smooth firing rate curve is observed (e.g., the curve for Neff = 50). In particular, at the critical point at which the bistability disappears, the gain in the response curve is the most rapid, as can be seen in Fig. 5a.
The transition also occurs when we change the relative contributions of fast and slow excitation. NMDA receptors act on a longer time-scale, and each postsynaptic conductance (PSC) has a smaller temporal variance than a PSC mediated by α-amino-3-hydroxy-5-methyl-4-isoxazolepropionic acid (AMPA) receptors. Therefore, by beginning with a sparse system and very little NMDA excitation, there are large fluctuations, but these fluctuations diminish and the system becomes more mean-driven, with an increasing proportion of NMDA excitation. Fig. 5b displays the complex cell population firing rate as a function of Ginput in networks of fixed Neff = 25 but with different NMDA/AMPA ratios. Again, the firing rate curves are obtained by increasing and decreasing Ginput. In the case with no AMPA, hysteresis is observed, and the dynamics is bistable. In the case with no NMDA, there is no hysteresis, and the dynamics is dominated by fluctuations and below the near-critical state. We note that the results in Fig. 5 a and b also hold in densely coupled networks where a probability of synaptic failure introduces an effective sparsification to the network connectivity, and so induces a similar bifurcation structure.§§
As seen in Fig. 5, dynamics of bistability corresponds to mean-driven dynamics, and strong fluctuations can modify the dynamics such that the bistability is removed either by increase in sparsity or decrease in percentage of NMDA. The synaptic fluctuations have the effect of smoothing the relation between synaptic input and neuronal output in the form of spikes. With sufficiently strong recurrent excitation, as we increase the strength of synaptic fluctuations, the region of bistability in neuronal output shrinks to achieve near-hysteresis at a critical level of intrinsic fluctuations. We call this region near-critical. As we increase fluctuations even further, the network is no longer hysteretic, and the gain is further decreased. Because this transition occurs as the amount of intrinsic synaptic fluctuations is varied, we call this fluctuation-controlled critical transition. The network dynamics at near-criticality is characterized by near-bistability and rapidly changing firing rates as a function of synaptic input. We note that it is the sparsity in network couplings that allows the network to maintain sufficiently strong intrinsic fluctuations in this near-critical region to achieve a stable high gain; this near-criticality high gain, in turn, gives rise to orientation selectivity for complex cells in the V1 model.
Discussion
The emerging picture of the functioning cortical network is one operating in states controlled by fluctuations (14, 26, 27). We studied here a large-scale cortical model of a V1 hypercolumn whose dynamics is dominated by intrinsic fluctuations in a critical state. The critical level of these intrinsic fluctuations is induced by sparse but efficacious circuitry. This model reproduces many experimentally measured aspects of cortical response. By building upon our previous V1 model, this network produces a continuum of simple and complex cell responses, with a bimodally distributed F1/F0 distribution for extracellular spiking, and unimodally distributed F1/F0 for intracellular potential, reflecting the egalitarian nature of its connectivity. Unlike our previous densely coupled model, in which fluctuations were created by means of external noise, in the current model, sparsity-induced intrinsic fluctuations provide a more general stability against the effects of self-excitation, and the fluctuation-controlled criticality gives rise to the emergence of well tuned complex cells. The population also shows contrast invariant tuning. As has been reported from experimental studies (16), we find a relative independence of orientation selectivity of firing rates from cortical location relative to the pinwheel center of the hypercolumn. As has also been reported (16), we find systematic differences in the selectivity of intracellular membrane conductances and potential. In iso-orientation domains, conductances and potential show like selectivity with extracellular spiking, whereas near pinwheel centers, the cortical inputs are generally more broadly tuned and variable, reflecting the haphazard nature of local connectivity to cells of different preferred orientation. We remark that these network properties are achieved with a circuit entirely local to the V1 hypercolumn, wherein sharp tuning in iso-orientation domains is accomplished by a reciprocal amplifying circuit involving both simple and complex cells. In particular, we need not postulate tuned inputs from extra-hypercolumn areas (16).
Much work has focused on the smoothing effect of fluctuations on the transfer of intracellular currents to extracellular spiking, and their relation to contrast invariant orientation tuning (14, 28, 29). Although our fluctuation-dominated network model of V1 shares these properties, its operating point is one of near-criticality, at the onset of a bifurcation of multistability and hysteresis, itself controlled by the level of intrinsic fluctuations in the network. Near criticality is typified by rapid and stable gain through self-excitation and underlies the good selectivity of complex cells in our model. As we show in a simple idealized model, a near-critical operating state can be attained by adjusting the level of intrinsic fluctuation by systematically varying the sparsity of connectivity, as well as by adjusting frequency of synaptic failure, or in a sparsely coupled network, by altering the relative strength of NMDA- to AMPA-mediated excitation. We point out that, if the percentage Λ of NMDA is sufficiently increased from our current V1 model with other parameters fixed (in particular, the input contrast remains the same), the complex cells move away from near-criticality and become unresponsive. This result is consistent with the behavior of the lower-branch response curve in the bistability region, as seen in Fig. 5b, if synaptic inputs are not sufficiently strong to drive the complex cells up to the higher firing upper-branch.
Our analysis suggests that pharmacological manipulations of the cortical network can change its operating point. For example, a mean-driven, hysteretic state can be moved toward the critical state by decreasing Λ, the relative contributions of slow and fast excitation. Similarly, we can move a nonselective network strongly dominated by fluctuations toward the critical state by increasing Λ. Although the Neff and Λ of the V1 cortical network are not known, our work suggests that the cortical network operates near a fluctuation-controlled critical state.
Methods
We use systems of conductance-based integrate-and-fire neurons, whose individual membrane potentials vPj(t) follow
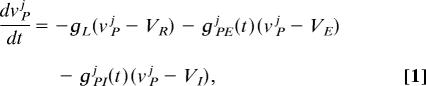 |
where P = E,I for the excitatory and inhibitory neurons, j = 1, …, NP. The mth spike time, tmj, of the jth model neuron, is determined by vPj(tmj−) = VT; vPj(tmj + τref) = VR, where τref is an absolute refractory period. Here, the membrane potentials of the excitatory (E) [inhibitory (I)] neurons are denoted by vEj(vIj), where the superscript j indexes the spatial location of the neuron within the network. 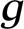 L,
L, 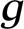 PE, and
PE, and 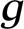 PI are the leak, excitatory, and inhibitory conductances, respectively. We use normalized, dimensionless potentials with VI = −2/3, VT = 1, VR = 0, and VE = 14/3 (11). We take τref = 3 ms (1 ms) for excitatory (inhibitory) neurons. Eq. 1 can be rewritten as dvPj/dt = −
PI are the leak, excitatory, and inhibitory conductances, respectively. We use normalized, dimensionless potentials with VI = −2/3, VT = 1, VR = 0, and VE = 14/3 (11). We take τref = 3 ms (1 ms) for excitatory (inhibitory) neurons. Eq. 1 can be rewritten as dvPj/dt = −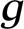 PTj(t)[vPj − VSj(t)], where
PTj(t)[vPj − VSj(t)], where 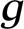 PTj ≡
PTj ≡ 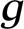 L +
L + 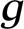 PEj +
PEj + 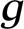 PIj is the total membrane conductance and VSj ≡ (
PIj is the total membrane conductance and VSj ≡ (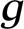 LVR +
LVR + 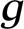 PEjVE +
PEjVE + 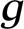 PIjVI)/
PIjVI)/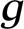 PTj is an effective reversal potential.
PTj is an effective reversal potential.
The time-dependent conductances arise from the LGN input and from the cortical network activity of the excitatory and inhibitory populations, and have the general form
 |
where FPE(t) = λj lgnj(t) [the conductance
lgnj(t) [the conductance  lgnj(t) denotes the feedforward forcing from the LGN (see the supporting text of ref. 13 for details)] and FPI(t) = cinhΣiGI(t − s lj) is a stimulus-independent inhibition driven by homogeneous Poisson spike trains. The PSCs have the form G(t) = Θ(t)[exp(−t/τd) − exp(−t/τr)]/(τd − τr), where Θ is the Heaviside function (G is normalized to have unit time integral). The time constants are τr = 1, 2, and 1 ms and τd = 5, 80, and 10 ms for excitatory AMPA and NMDA and inhibitory GABAA, respectively. (Note that orientation-tuning properties in our model are similar for τd = 3 and 5 ms for AMPA and GABAA, respectively.) For excitatory synapses, GE(t) = (1 − Λ)GAMPA(t) + ΛGNMDA(t), where Λ denotes the fractional contribution of NMDA receptors, Λ = 25%.
lgnj(t) denotes the feedforward forcing from the LGN (see the supporting text of ref. 13 for details)] and FPI(t) = cinhΣiGI(t − s lj) is a stimulus-independent inhibition driven by homogeneous Poisson spike trains. The PSCs have the form G(t) = Θ(t)[exp(−t/τd) − exp(−t/τr)]/(τd − τr), where Θ is the Heaviside function (G is normalized to have unit time integral). The time constants are τr = 1, 2, and 1 ms and τd = 5, 80, and 10 ms for excitatory AMPA and NMDA and inhibitory GABAA, respectively. (Note that orientation-tuning properties in our model are similar for τd = 3 and 5 ms for AMPA and GABAA, respectively.) For excitatory synapses, GE(t) = (1 − Λ)GAMPA(t) + ΛGNMDA(t), where Λ denotes the fractional contribution of NMDA receptors, Λ = 25%.
The kernels aj,k and bj,k describe the spatial structure of the cortical coupling and are normalized to have unit sum. The parameter λj ∈ [0, 1] in these equations indicates heuristically how the distribution of simple and complex cells is set in our models and characterizes the simple-complex nature of the jth neuron (with λj = 0 the most complex, λj = 1 the most simple; SPE0 models weak cortical excitatory couplings for simple cells), by setting the strength of LGN drive relative to the strength of the cortico-cortical excitation. The parameter λj is distributed uniformly in [0, 1] for our large-scale V1 model.
The factor pkj/p controls the degree of sparsity in network connectivity, while simultaneously scaling up the strength of individual connections as connectivity is made more sparse. To wit, pkj is chosen to be 1 with probability p and zero otherwise, and is fixed for individual realizations of the network. On average, each neuron is coupled presynaptically to Neff = pN other neurons. By scaling the strength of a single postsynaptic connection by p, sparser networks have stronger PSCs, with the mean and the variance of a PSC induced in a single cell scaling as 1/Neff. As the distributional average of pkj/p is one, the parameters SPE and SPI denote overall network synaptic strengths. To examine the effects of synaptic fluctuations, we study networks with the fixed network coupling parameters SPP but differing levels of sparsity. We take SEI = SII so that the cortical inhibition is the same for both excitatory and inhibitory neurons.
The network architecture is a simplified version of the model of ref. 13. The basic cortical architecture, LGN drive, and cortico-cortical couplings are described in detail in refs. 11, 12, and 13. However, unlike these previous works, here we do not model feedback from other layers or extrastriate areas, which was modeled as activity-dependent feedback in ref. 13. We set the synaptic coupling parameters to be fixed constants instead of being Gaussian distributed about a mean. Inhibitory effects are modeled as a sum of local and global contributions: bj,k = (1/2) × (bj,k0 + 1/Neff). The first term is the local one with bj,k0 a Gaussian in the distance between neurons j and k and is normalized to unity, and the second is global and scaled with Neff. Unlike our previous model, we do not consider a second, long inhibitory synaptic time course.
For the idealized model, we have  PEj(t) = η jGinput,PE(t) + SPE(σ)Σk(pkj/pN)ΣlGE(t − tlk), and
PEj(t) = η jGinput,PE(t) + SPE(σ)Σk(pkj/pN)ΣlGE(t − tlk), and 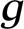 PIj(t) = SPIΣk(pkj/pN)ΣlGI(t − tlk), with ηj = 1, σ = s for j = 1, 2, …, NP/2 and ηj = 0, σ = c, otherwise. NE = 75%N, NI = 25%N, and N = 1600 is the total number of neurons in the network. Neff = pN. Ginput,PE = ƒΣlGP(t − tk), where {tk} is a Poisson spike train with constant rate ν0.
PIj(t) = SPIΣk(pkj/pN)ΣlGI(t − tlk), with ηj = 1, σ = s for j = 1, 2, …, NP/2 and ηj = 0, σ = c, otherwise. NE = 75%N, NI = 25%N, and N = 1600 is the total number of neurons in the network. Neff = pN. Ginput,PE = ƒΣlGP(t − tk), where {tk} is a Poisson spike train with constant rate ν0.
Acknowledgments
This work was supported by National Science Foundation (NSF) Grant DMS-0506396 (to L.T., D.C., D.W.M., and M.J.S.). In addition, this work was supported by NSF Grant DMS-0211655 (to D.C. and D.W.M.).
Abbreviations
- CV
circular variance
- V1
primary visual cortex
- F1
first Fourier component
- F0
mean component
- LGN
lateral geniculate nucleus
- ES
excitatory simple
- EC
excitatory complex
- PSC
postsynaptic conductance
- AMPA
α-amino-3-hydroxy-5-methyl-4-isoxazolepropionic acid.
Footnotes
Conflict of interest statement: No conflicts declared.
Orientation selectivity for drifting grating stimuli is measured by CV. Let m(θ) denote the time-averaged firing rate as a function of stimulus angle θ; m(θ) is π-periodic. CV is defined as CV[m] = 1 − |∫0πm(θ)e2iθdθ|/∫0πm(θ)dθ. CV lies between 0 and 1. Poorly tuned cells have CVs near 1, whereas well tuned cells have CVs near 0.
We note that Eq. 1 of the integrate-and-fire dynamics can be cast in the form v̇j = −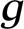 Tj(t)[v j − VSj(t)] (see Methods). The effective reversal potential, VSj, is necessarily greater than the voltage threshold VT whenever the neuron fires. We say the dynamics are mean-driven whenever the trial averaged 〈VSj(t)〉 > VT; i.e., the mean of the synaptic input is sufficient to drive the neuron to fire. The time-average V̄Sj ≡ T−1∫t0t0+TVSj(t)dt can also be used if the rate of the input is time-homogeneous. For 〈VS〉 < VT; we say the dynamics are fluctuation-driven, because temporal fluctuations in the drive are needed for spiking.
Tj(t)[v j − VSj(t)] (see Methods). The effective reversal potential, VSj, is necessarily greater than the voltage threshold VT whenever the neuron fires. We say the dynamics are mean-driven whenever the trial averaged 〈VSj(t)〉 > VT; i.e., the mean of the synaptic input is sufficient to drive the neuron to fire. The time-average V̄Sj ≡ T−1∫t0t0+TVSj(t)dt can also be used if the rate of the input is time-homogeneous. For 〈VS〉 < VT; we say the dynamics are fluctuation-driven, because temporal fluctuations in the drive are needed for spiking.
Note that convergent feedforward input from many LGN neurons sets up an orientation preference, laid out as pinwheel patterns, each with an orientation preference singularity at its center (11).
In our model, the sparsity-induced, intrinsic cortico-cortical conductance fluctuations are 10–20 times larger than the fluctuations in the LGN input as measured by the standard deviation. Our notion of fluctuation-driven dynamics is distinct from the dynamics of a “balanced network” where the overall excitatory and inhibitory currents nearly cancel (21). (Network models in Results are fluctuation-driven, with the mean synaptic currents being strongly inhibitory and the Vs usually being far below threshold.) In our large V1 model, a typical selective ES(EC) has VS = 0.045(0.075) ± 0.362(0.373), pS = 0.0042(0.0066) in the background (where pS is the probability of VS ≥ VT) and has VS = 0.192(0.333) ± 0.432(0.501), pS = 0.031(0.092) under a medium contrast stimulus. If the fluctuation had remained the same under driving, i.e., σVS = 0.362(0.373) but the mean changed from μVS = 0.045(0.075) to 0.192(0.333), then the evoked pS is estimated to be p1 = 0.0129(0.037) by approximating the distribution of VS with a normal distribution. On the other hand, if the mean had remained the same, i.e., μVS = 0.045(0.075) but σVS changed from σVS = 0.362(0.373) to 0.432(0.501), then the evoked pS is estimated to be p2 = 0.0135(0.033). Clearly, the fact that neither p1 nor p2 is close to the true pS = 0.031(0.092), which is a factor of 2–3 larger than p1,2, suggests that both the mean and fluctuations in the network are equally important in controlling the tuning dynamics.
Shapley, R., Johnson, E., Hawken, M. & Kang, K. (2002) Soc. Neurosci. Abstr. 32, 720.8.
It is important to note that there can be important differences in network response between the effective sparsification via synaptic failure and that via sparse connections that are fixed and independent of time. For example, synaptic failure induces a much more statistically homogeneous dynamic behavior in a network, whereas the sparse but fixed connections can have clustered dynamics associated with specific causal links over different clusters of a network. We have found (data not shown) that, using synaptic failure to effectively sparsify our V1 network, that is, through the statistical randomization of spiking, complex cells near pinwheel centers are less tuned than those in orientation domains, i.e., bearing more resemblance to the results of our previous, densely connected cortical model (13) than to the current model with haphazard connections, for which the tuning of complex cells arises by means of clustered, local dynamics.
References
- 1.De Valois R., De Valois K. Spatial Vision. Oxford: Oxford Univ. Press; 1988. [Google Scholar]
- 2.Skottun B. C., De Valois. R. L., Grosof D. H., Movshon J. A., Albrecht D. G., Bonds A. B. Vision Res. 1991;31:1079–1086. doi: 10.1016/0042-6989(91)90033-2. [DOI] [PubMed] [Google Scholar]
- 3.Sompolinsky H., Shapley R. Curr. Opin. Neurobiol. 1997;7:514–522. doi: 10.1016/s0959-4388(97)80031-1. [DOI] [PubMed] [Google Scholar]
- 4.Ferster D., Miller K. D. Annu. Rev. Neurosci. 2000;23:441–471. doi: 10.1146/annurev.neuro.23.1.441. [DOI] [PubMed] [Google Scholar]
- 5.Hubel D., Wiesel T. J. Physiol. (London) 1968;195:215–243. doi: 10.1113/jphysiol.1968.sp008455. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Troyer T., Krukowski A., Priebe N., Miller K. J. Neurosci. 1998;18:5908–5927. doi: 10.1523/JNEUROSCI.18-15-05908.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Somers D., Nelson S., Sur M. J. Neurosci. 1995;15:5448–5465. doi: 10.1523/JNEUROSCI.15-08-05448.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Carandini M., Ringach D. L. Vision Res. 1997;37:3061–3071. doi: 10.1016/s0042-6989(97)00100-4. [DOI] [PubMed] [Google Scholar]
- 9.Adorjan P., Levitt J., Lund J., Obermayer K. Vis. Neurosci. 1999;16:303–318. doi: 10.1017/s0952523899162114. [DOI] [PubMed] [Google Scholar]
- 10.Ben-Yishai R., Bar-Or R., Sompolinsky H. Proc. Natl. Acad. Sci. USA. 1995;92:3844–3848. doi: 10.1073/pnas.92.9.3844. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.McLaughlin D., Shapley R., Shelley M., Wielaard J. Proc. Natl. Acad. Sci. USA. 2000;97:8087–8092. doi: 10.1073/pnas.110135097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Wielaard D. J., Shelley M., McLaughlin D., Shapley R. J. Neurosci. 2001;21:5203–5211. doi: 10.1523/JNEUROSCI.21-14-05203.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Tao L., Shelley M., McLaughlin D., Shapley R. Proc. Natl. Acad. Sci. USA. 2004;101:366–371. doi: 10.1073/pnas.2036460100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Anderson J., Lampl I., Gillespie D., Ferster D. Science. 2000;290:1968–1972. doi: 10.1126/science.290.5498.1968. [DOI] [PubMed] [Google Scholar]
- 15.Cai D., Tao L., Shelley M., McLaughlin D. Proc. Natl. Acad. Sci. USA. 2004;101:7757–7762. doi: 10.1073/pnas.0401906101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Marino J., Schummers J., Lyon D., Schwabe L., Beck O., Wiesing P., Obermayer K., Sur M. Nat. Neurosci. 2005;8:194–201. doi: 10.1038/nn1391. [DOI] [PubMed] [Google Scholar]
- 17.Ringach D., Shapley R., Hawken M. J. Neurosci. 2002;22:5639–5651. doi: 10.1523/JNEUROSCI.22-13-05639.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Mechler F., Ringach D. Vision Res. 2002;42:1017–1033. doi: 10.1016/s0042-6989(02)00025-1. [DOI] [PubMed] [Google Scholar]
- 19.Priebe N., Mechler F., Carandini M., Ferster D. Nat. Neurosci. 2004;7:1113–1122. doi: 10.1038/nn1310. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Chance F., Nelson S., Abbott L. Nat. Neurosci. 1999;2:277–282. doi: 10.1038/6381. [DOI] [PubMed] [Google Scholar]
- 21.van Vreeswijk. C., Sompolinsky H. Neural Comp. 1998;10:1321–1371. doi: 10.1162/089976698300017214. [DOI] [PubMed] [Google Scholar]
- 22.Maldonado P., Godecke I., Gray C., Bonhoeffer T. Science. 1997;276:1551–1555. doi: 10.1126/science.276.5318.1551. [DOI] [PubMed] [Google Scholar]
- 23.Schummers J., Marino J., Sur M. Neuron. 2002;36:969–978. doi: 10.1016/s0896-6273(02)01012-7. [DOI] [PubMed] [Google Scholar]
- 24.Mason A., Nicoli A., Stratford K. J. Neurosci. 1991;11:72–84. doi: 10.1523/JNEUROSCI.11-01-00072.1991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Thomson A. M., West D. C., Wang Y., Bannister A. P. Cereb. Cortex. 2002;12:936–953. doi: 10.1093/cercor/12.9.936. [DOI] [PubMed] [Google Scholar]
- 26.Shadlen M. N., Newsome W. T. J. Neurosci. 1998;18:3870–3896. doi: 10.1523/JNEUROSCI.18-10-03870.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Rudolphe M., Destexhe A. Neural Comp. 2003;15:2577–2618. doi: 10.1162/089976603322385081. [DOI] [PubMed] [Google Scholar]
- 28.Miller K., Troyer T. J. Neurophysiol. 2002;87:653–659. doi: 10.1152/jn.00425.2001. [DOI] [PubMed] [Google Scholar]
- 29.Hansel D., van Vreeswijk C. J. Neurosci. 2002;22:5118–5128. doi: 10.1523/JNEUROSCI.22-12-05118.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]