Abstract
The “coil library,” consisting of the φ, ψ values of residues outside secondary structure in high-resolution protein structures, has chiefly the β, αR, αL, and polyproline II backbone conformations. In denatured proteins, the 20 aa have different average values of the 3JHNα coupling constant, related to the backbone angle φ by the Karplus relation. Average 3JHNα values obtained from the distributions of φ, g(φ), of the coil library agree with NMR results, and so the coil library can be and is being used to model denatured proteins. Here, Monte Carlo simulations of backbone conformations in denatured proteins are used to test two physics-based models: the random coil model of Brant and Flory [(1965) J. Am. Chem. Soc. 87, 2788–2791 and 2791–2800] and an electrostatic screening model (ESM) that includes electrostatic solvation. The random coil model represents hindered rotation about φ and ψ backbone angles, nonbonded interactions, and dipole–dipole interactions. In the ESM, the nonbonded interactions term is replaced by the use of hard sphere repulsion and allowed regions in the Ramachadran maps. These models were tested by using the amino acid sequences of three small proteins. There are two main conclusions: (i) The g(φ) distributions of the coil library contain detailed, specific information, so that prediction of the g(φ) distributions of the different amino acids is a demanding test of the energy function. (ii) The ESM is partly successful in predicting the g(φ) distributions. Electrostatic solvation is primarily responsible, and steric clash between pairs of atoms connected by torsion angles is not responsible.
Our aim is to find an energy function that reproduces the backbone conformations of amino acids in denatured proteins when the conformations are simulated by the Monte Carlo method. Recent evidence indicates that the type of amino acid specifies its preference for certain backbone conformations [β, polyproline II (PII), αL, and αR] in denatured proteins. Average values of the 3JHNα coupling constant differ substantially among the amino acids in denatured proteins and short peptides (1, 2), and the 3JHNα coupling constant is directly related to the backbone angle φ by the Karplus relation (3). The coil library (residues outside regular secondary structures in high-resolution protein structures) is being used as a provisional database for backbone conformations of denatured proteins (1, 2, 4). We seek to predict the distribution of φ, g(φ), for the various amino acids in the coil library. This requires understanding the energetics of interconversion between backbone conformations as a function of φ. To simplify the problem, we limit consideration here to the interconversion between β and PII by restricting φ and ψ so as to exclude αR and αL, by taking (90 < ψ < 180) and (0 > φ > −180).
We test two models. The first is the random coil model (RCM) introduced by Flory and coworkers (5–8), who argued that the backbone conformations and chain dimensions of denatured proteins can be predicted by specifying a small set of energy terms, an approach used successfully with synthetic flexible polymers. The second model is an electrostatic screening model (ESM), based on the proposal by Avbelj and Moult (9) that peptide backbone conformations should strongly depend on the role of side chains in determining the extent of screening by water of the peptide dipole–dipole interactions.
The modern approach to understanding protein conformation is to make all-atom simulations of conformation using a comprehensive molecular force field. However, this approach has not been successful in modeling backbone conformations of denatured proteins, apparently because the energy differences between backbone conformations are smaller than the overall accuracy of present force fields (10, 11). It seems reasonable then to return to the simpler approach of predicting a small set of terms that should control backbone conformation in flexible chain polypeptides that are not close-packed, unlike native proteins.
The RCM of Flory and coworkers (5-8) was developed originally for use with simple peptides such as Ala–Gly copolymers. Its energy function contains terms for Coulombic interaction between partial charges on the peptide NH and CO dipoles, nonbonded interactions between pairs of atoms, and hindered rotation about the backbone φ and ψ angles. Flory and coworkers considered solvation of the peptide backbone only by allowing uniform screening by solvent of the peptide dipole–dipole interactions, through using a dielectric constant of 3.5. The ESM differs importantly from the RCM by including the interaction between solvent and the peptide dipoles, calculated as the electrostatic solvation free energy (ESF), using the delphi algorithm and the parse parameter set (12). The parse parameters (partial charges and atomic radii) have been calibrated against a database of experimental solvation free energies for model compounds including amides (12), so that the ESF values of model compounds are calibrated against experiment. Calculations of ESF values show that they depend primarily on the arrangement of the partial charges and their access to solvent, which in a peptide or protein system strongly depends on nearby side chains (13–16).
Flory and coworkers (5–8) considered that the nonbonded interactions are an important factor determining backbone conformations in denatured proteins, and some workers agree with this view (17–19). To test whether the nonbonded interactions term can be responsible for the variation in g(φ) seen in the coil library, we replaced the nonbonded interaction term in the ESM with hard sphere repulsion without, however, checking pairs of atoms connected by torsion angles for steric clash. We also required that φ, ψ values fall within the allowed regions of the Ramachandran maps. Then we tested whether some factor other than ESF can be responsible for the partial success of the ESM by setting the ESF term = 0 in the ESM energy function and made related tests.
These tests were made by using the amino acid sequences of three small proteins: protein G, ubiquitin, and barnase.
Methods
Representation of Protein Molecules.
Protein molecules are represented by including all heavy atoms and polar hydrogens. In the RCM, the residue geometry and other properties of the protein molecule are as described by Brant et al. (8). In the ESM, the geometry of the amino acids is generated by using the Discover residue library (20). The torsion angle ω of the peptide bond is held fixed at 180° and planar groups are kept exactly planar. In the ESM hard sphere repulsion is enforced by discarding conformations with steric clash when any pair of nonbonded atoms is closer than 0.7 Å less than the sum of the van der Waals radii given by Chothia (21), but pairs of atoms connected by torsion angles are not checked for steric clash. Steric clash occurs when main-chain N and O atoms are closer than 2.5 Å. The offset of 0.7 Å was chosen to ensure that few steric clashes are found in high-resolution protein structures and that the complete allowed regions of the Ramachandran maps are found when the conformations of denatured proteins are simulated. The Monte Carlo simulations of the ESM do not depend on the value of the offset if it is >0.4 Å.
All residues, both inside and outside secondary structures of 1,476 high-resolution protein structures, are included when determining the allowed regions used with the ESM. The bin size for φ and ψ is 5° and a bin is considered to be within the allowed region if it contains at least 10 residues from a total of 9,000 residues of the same type. In the Monte Carlo simulations each allowed bin has the same probability of being drawn.
The coil library of backbone conformations is constructed from all pairs of φ, ψ angles for residues outside secondary structure in 1,476 high-resolution protein structures.
Energy Function of the ESM.
The energy function of the protein molecule in the ESM is a sum of contributions expressed by Eq. 1.
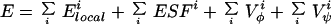 |
1 |
in which each sum runs over all amino acids i in the sequence. In addition, the chain must be free of steric clashes, as described above.
The term E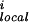 is the local main-chain electrostatic energy of residue i, computed as described by Avbelj and Moult (9). It depends on the interaction of main-chain NH and CO groups in residue i with the CO and NH groups of residues i + 1, i − 1, i + 2, and i − 2. E
is the local main-chain electrostatic energy of residue i, computed as described by Avbelj and Moult (9). It depends on the interaction of main-chain NH and CO groups in residue i with the CO and NH groups of residues i + 1, i − 1, i + 2, and i − 2. E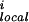 is computed by using Coulomb's law with a dielectric constant of 1. Point atomic charges for the main-chain atoms N, HN, C, and O are −0.28, +0.28, +0.38, and −0.38 electrons, respectively (14).
is computed by using Coulomb's law with a dielectric constant of 1. Point atomic charges for the main-chain atoms N, HN, C, and O are −0.28, +0.28, +0.38, and −0.38 electrons, respectively (14).
The quantity ESFi is the backbone ESF of amino acid residue i (14). It is calculated by the finite difference Poisson–Boltzmann method (12, 14) by using the parse-neutral parameter set (14) in which the parse point atomic charges of side-chain atoms (12) are set to zero. Atomic point charges in all side chains, as well as formal charges in ionizing side chains, are set to zero in this article. The electrostatic potential of the whole molecule is first calculated by using a very large box and large grid size (scale = 0.20, perfil = 65). This potential then provides boundary conditions for much more accurate calculations of electrostatic potential around each residue (focusing). Equal box and grid sizes (scale = 2.0, grid size 51, center at Cα) are then used for all residues to ensure approximately equal amounts of water near each residue.
The quantities V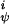 and V
and V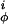 are the intrinsic torsional potentials around the angles ψ and φ
are the intrinsic torsional potentials around the angles ψ and φ
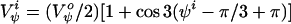 |
2 |
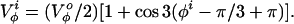 |
In the ESM the constant V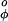 is set to 2.5 kcal/mol while the constant V
is set to 2.5 kcal/mol while the constant V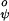 is set to zero.
is set to zero.
Finding the correct balance between these terms is critical for obtaining correct results. Earlier studies (12–14) have given estimates of both ESF and Elocal and these terms are used without change; only the value of V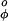 has been adjusted here.
has been adjusted here.
Energy Function of the RCM.
The energy function of the RCM is taken from the work of Brant and Flory (6, 7) and Brant et al. (8). Some other representations of the nonbonded interaction terms were also tested. The energy function of the RCM of Brant et al. (8) is a sum of contributions expressed by Eq. 3.
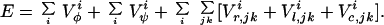 |
3 |
The intrinsic torsional potentials V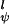 and V
and V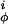 are as in Eq. 2 with V
are as in Eq. 2 with V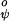 = 1.0 kcal/mol and V
= 1.0 kcal/mol and V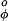 = 1.5 kcal/mol (8). The repulsive term of the nonbonded interactions is expressed by
= 1.5 kcal/mol (8). The repulsive term of the nonbonded interactions is expressed by
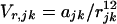 |
4a |
and the attractive (London) term is expressed by
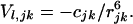 |
4b |
The coefficients ajk and cjk are found from the Slater–Kirkwood equation as described (8). The Coulombic term, which gives the interaction between monopoles δj and δk, is
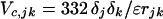 |
4c |
in which ɛ, the effective dielectric constant, has the value 3.5. The partial charges differ only slightly from those in the ESM: 0.281 (RCM) versus 0.28 (ESM) and 0.394 (RCM) versus 0.38 (ESM). The attractive part of the nonbonded interaction is set to zero for atoms more than two residues apart, to account for screening of the Coulomb interactions in aqueous solution. The bond distances and angles are those of Brant and Flory (6, 7).
Monte Carlo Simulation Procedure.
The starting geometry in all simulations is a random conformation, achieved as follows. The backbone torsion angles are randomly selected from the allowed regions in the Ramachandran plots, taken from both inside and outside secondary structures. In the ESM the side-chain torsion angles are randomly selected from the entire library of side-chain torsion angles (both inside and outside secondary structure) whereas in the RCM all side-chain torsion angles are drawn with equal probability. The initial conformation is then relaxed by small variations in torsion angles to remove steric overlaps between pairs of atoms. To improve sampling of conformational space, a large number (≈100) of independent Monte Carlo simulations are performed, each with 5,000 steps. The initial 1,500 steps are needed to achieve clash-free equilibration. Only torsion angles are allowed to vary during simulations, but both side-chain and backbone torsion angles vary.
Conformational space is sampled by varying the torsion angles by using two types of moves, in which either main-chain or side-chain torsion angles are selected. A residue is selected randomly. The probabilities of selecting either main-chain or side-chain torsion angles are set to 60% and 40%, respectively. In the ESM torsion angles φ and ψ are always selected as pairs from the coil library and are required to lie within the allowed regions of the Ramachandran maps of the various residues (see above). Likewise, side-chain torsion angles are selected at random from the entire library. The resulting conformation is tested for steric clashes and discarded if any steric clash is found.
The energy of a conformation is computed from Eq. 1 (ESM) or Eq. 3 (RCM). If the energy decreases, the new conformation is accepted. If the energy increases, the Metropolis criterion (22) is used to decide whether to accept or reject the move. The temperature is 300 K. Overall, two-thirds of the moves are accepted during simulations. Average values are computed from the large number of conformations (>105) present after equilibration.
3JHNα Coupling Constants.
The 3JHNα coupling constants of residues are calculated from their φ values by the Karplus equation (3).
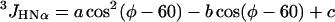 |
5 |
(φ in degrees). Four somewhat different parameterizations of Eq. 5 have been given in the literature, with the following parameters: a = 6.4, b = −1.4, c = 1.9 (23); a = 6.6, b = −1.3, c = 1.5 (24); a = 6.51, b = −1.76, c = 1.60 (25); and a = 7.90, b = −1.05, c = 0.65 (26). Values of 3JHNa for a given residue were computed as the average of the values obtained with Eq. 5 by using the four different sets of parameters. Further averaging, to obtain 〈3JHNα〉, was then done over all residues of a given type. Note that Eq. 5 gives a value of JHNα near 5 for φ near −70°, and a value close to 10 for φ near −120°.
Fitting g(φ) to Two Gaussians.
The procedure used to fit g(φ) to a sum of two Gaussian functions is based on a standard Levenberg–Marquardt fitting algorithm as described (27).
Results
3JHNα Coupling Constants from the Coil Library Compared with Experimental Values.
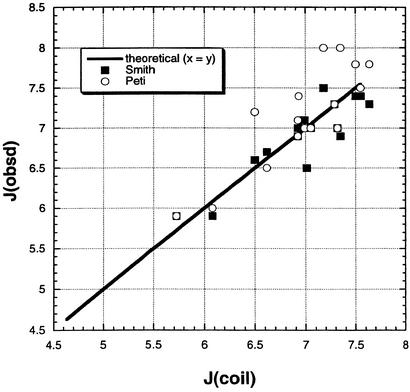
The number of high-resolution structures in the Protein Data Bank is large and increasing rapidly. As a result, the distributions of φ, ψ backbone angles in the coil library are very reliable. Previous authors found a good correlation between coupling constants measured by NMR and ones computed from φ values of the coil library (1, 2, 28, 29). Fig. 1 shows new data from the coil library testing this previous result. The predicted coupling constants from the coil library (see Methods) are compared with two sets of experimental results, one for unstructured peptides (2) and one for denatured ubiquitin (29). The coupling constants predicted from the coil library agree with both sets of experimental data better than the two experimental data sets agree with each other. The lackluster agreement between the two experimental data sets may reflect different neighboring residue effects, which average out in the larger data set from the coil library.
Figure 1.
Measured 3JHNα coupling constants for the various amino acid residues plotted against predicted values from the structural coil library. The values from the coil library are based on φ values in protein structures and the Karplus relation between φ and 3JHNα (see Methods). The two sets of experimentally measured coupling constants are given for amino acid residues in unstructured peptides (2) and denatured ubiquitin (29). The complete coil library is used with −180 < ψ < 180 and −180 < φ < 180. The average values of 3JHNα in the coil library, which lie on the line, are (in Hz): G, 5.720; A, 6.075; E, 6.495; S, 6.615; R, 6.920; K, 6.920; D, 6.931; L, 6.991; W, 7.007; H, 7.177; N, 7.294; Y, 7.318; F, 7.351; I, 7.495; V, 7.547; T, 7.642.
Comparison Between 〈φ〉 Values from the Coil Library and from Simulations of the ESM and RCM.
The average value of φ (〈φ〉) is a useful parameter to use in comparing g(φ) distributions for different amino acids and their simulation by different models. The 〈φ〉 values given by the RCM fall in a high range (−106.2° to −116.5°) compared with the coil library values (−93.3° to −107.2°), whereas the ESM values (−95.1° to −109.8°) are closer to the coil library values. Values for Pro and Gly are excluded. Only the PII and β backbone conformations are analyzed by restricting φ and ψ to exclude the αL and αR conformations: 90 < ψ < 180 and −180 < φ < 0. (In the 〈J〉 values for the coil library given in the legend to Fig. 1, φ, ψ restriction is not applied because the coupling constants measured by NMR are averaged over all φ and ψ values.)
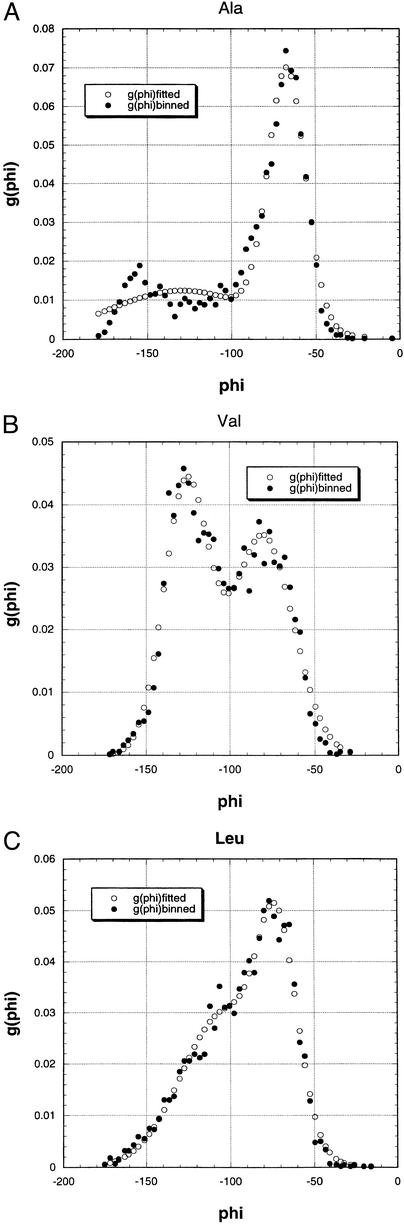
Fitting the g(φ) Distributions to a Sum of Two Gaussians.
Because of scatter in the binned distribution data for g(φ), the g(φ) distributions (proline excluded) are represented here by lines fitted to a sum of two Gaussians. One Gaussian is found to be centered on a band termed PII because the maximum value of g(φ) for all amino acids occurs close to the canonical PII band position, and the ψ value at this position also matches that of PII. The second Gaussian fits a β-region band whose size and position vary widely among the amino acid types. The quality of the fitting is illustrated in Fig. 2 for three examples taken from coil library g(φ) distributions. For all amino acids, the fit of the binned distribution data to a Gaussian for the PII band lies almost within the scatter of the data. For Ala (Fig. 2A), the overall g(φ) has two or more minor bands in the β region in addition to the major PII band, and consequently a fit to only two Gaussians fails to work well for Ala in the β region. Most fittings of g(φ) to a sum of two Gaussians work well in both the β and PII regions and resemble those for Val and Leu (Fig. 2 B and C) in giving a fit that lies within the scatter of the binned g(φ) data. Fitting g(φ) to a sum of two Gaussians works poorly for the variant ESM with ESF = 0 and Elocal scaled down by D = 3.5, and the two-Gaussian fits were not used.
Figure 2.
Three examples of fitting coil library g(φ) distributions (with 90 < ψ < 180 and −180 < φ < 0) to a sum of two Gaussians. (A) Alanine. (B) Valine. (C) Leucine. The bin size is 3° and g(φ) is not normalized.
Properties of the g(φ) Distributions in the Coil Library and the ESM and RCM Simulations.
Differences among the g(φ) distributions of the various amino acids in the coil library are illustrated in Fig. 2 for Ala, Val, and Leu. The differences reside chiefly in the size of the PII band and in both the size and position of the β-region band. The position of the PII band is relatively constant (see below). The g(φ) distribution of alanine is unusual in showing more than one band in the β region. An important conclusion from comparing the g(φ) distributions of the amino acids in the coil library is that the differences in g(φ) between amino acids are large enough and specific enough to provide a demanding test of any energetic model.
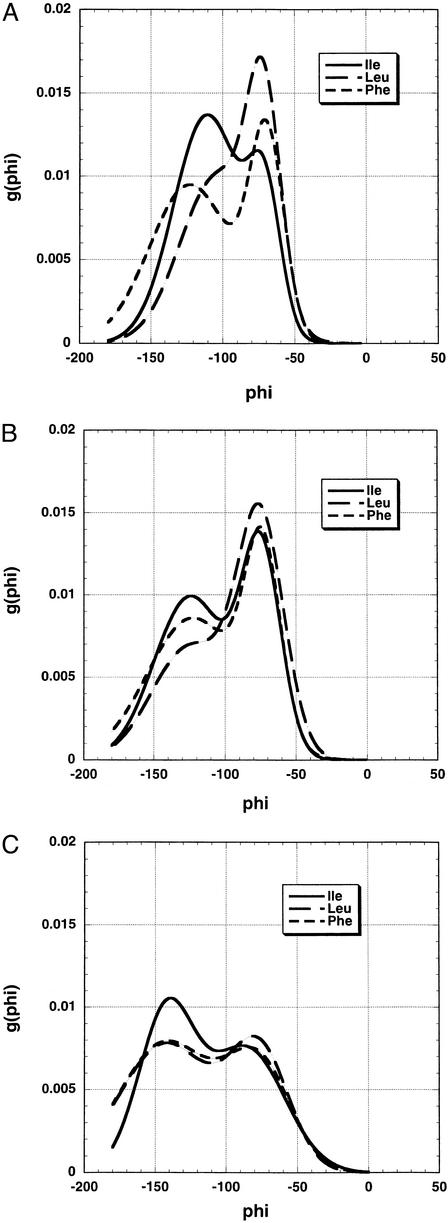
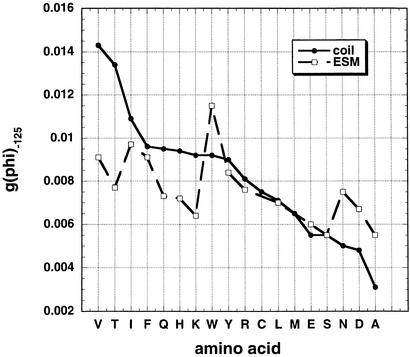
When the g(φ) distributions of Leu, Phe, and Ile are compared by overlaying the entire distribution curves (Fig. 3), the results show that g(φ) at −125° is a useful parameter for comparing the g(φ) distributions. This is evident in the coil library results (Fig. 3A) and the ESM results (Fig. 3B), but there is little variation in the RCM results (Fig. 3C). Results for all amino acids at −125° are shown in Fig. 4. (Gly, Pro, Cys, and Met are excluded because Pro, Cys, and Met are missing, whereas Gly and Pro have anomalous φ, ψ distributions.) The variation among amino acids in g(φ) at −125° is strong in the coil library, moderate in the ESM simulations, and quite small in the RCM simulations (see below and Fig. 5A). Importantly, the amino acid dependence of g(φ) at −125° is similar for the ESM simulations and the coil library.
Figure 3.
Comparison of g(φ) distributions, given by fitting binned data to a sum of two Gaussians, for three amino acids, Leu, Phe, and Ile, from the coil library (A), ESM simulations (B), and RCM simulations (C). The backbone conformations are restricted to PII and β by setting 90 < ψ < 180 and −180 < φ < 0. The bin size is 3°. Average values of ψ were determined for the bins at the maximum values of g(φ) in both the PII and β–region bands in Fig. 4. They correspond to typical values of ψ for these backbone conformations (data not shown).
Figure 4.
Plot of g(φ) at −125° versus amino acid type for the coil library and the ESM. Gly and Pro are excluded because of their unusual distributions of φ and ψ, whereas Cys and Met are not present in the three proteins whose conformations were simulated by the ESM. Note that the variation in g(φ) at −125° is similar in character in the coil library and the ESM simulations.
Figure 5.
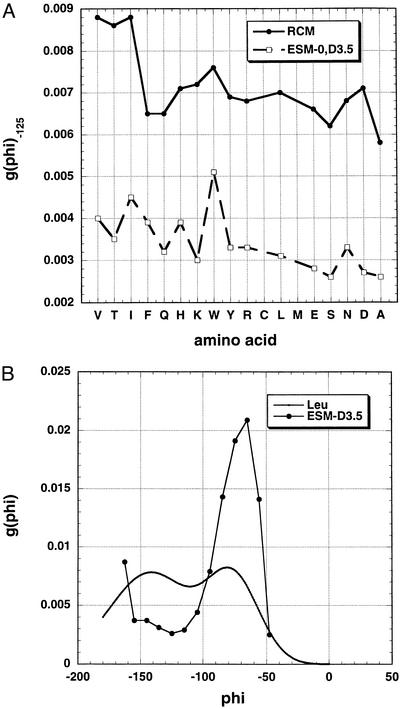
(A) Plot of g(φ) at −125° versus amino acid type for the RCM and the variant ESM-D3.5. In the variant ESM, ESF is set = 0 and Elocal is scaled down by using a dielectric constant of 3.5. Note the reduced variation with amino acid type shown by these two models as compared with the standard ESM (Fig. 4). The scale is the same as in Fig. 4. (B) Comparison of the g(φ) distributions for leucine given by the RCM and the variant ESM-D3.5.
The values of φ for the PII band in the coil library (Gly and Pro excluded), taken from the band centers of the fitted Gaussian curves, lie chiefly in the range between −67.2° and −73.9°, with Val, Thr, and Asn showing more negative values. In the simulations for the RCM of Brant and Flory (8) (Gly, Pro, Cys, and Met excluded), values of φ for the PII band lie in a more negative range between −75.5° and −88.0° with the β–branched amino acids Val, Ile, and Thr showing the highest negative values. In the ESM simulations (Gly, Pro, Cys, and Met excluded), values of φ for the PII band are intermediate between those of the coil library and the RCM and lie between −69.9° and −77.0° for all amino acids except Arg with −79.4°.
Varying Parameters in the RCM and ESM.
To test whether inclusion of ESF in the ESM is responsible for the variation in g(φ), a variant ESM (ESM-D3.5) was tested in which ESF = 0 and Elocal is reduced by setting the dielectric constant = 3.5, as in the RCM of Brant and Flory. The variant ESM-D3.5 shows considerably smaller variation in g(φ) among the amino acids than does the ESM. This point is illustrated in Fig. 5A, which shows the values of g(φ) at −125° for the different amino acids for both the variant ESM and the RCM. Both models show little variation in g(φ) among the different amino acids. Fig. 3C further illustrates the small extent of variation in g(φ) seen for the RCM. The values of g(φ) at −125° for the different amino acids are higher (i.e., more negative) for the RCM than for the variant ESM-D3.5. Fig. 5B shows the g(φ) distributions for leucine given by the two models and illustrates that the g(φ) distributions have characteristically different shapes for the two models.
Similar results for the RCM simulations of g(φ) were obtained when the nonbonded interaction terms were taken either from amber (30) or charmm (31) instead of from Brant et al. (8) (data not shown).
Discussion
Use of the Coil Library.
We compare the backbone conformations simulated for the RCM and ESM with the coil library rather than with experimentally measured coupling constants because the differences between various experimental sets of coupling constant data are too large (see Fig. 1). Because of scatter in the experimental data as well as differences between the two data sets, the coupling constants predicted for the RCM and ESM do not distinguish clearly between them (data not shown). On the other hand, using the g(φ) distributions from the coil library as a test of the RCM and ESM easily distinguishes between them. Future work may show significant differences between the coil library and backbone conformations in denatured proteins, because the coil library is taken from close-packed (but typically solvent-exposed) segments of structure in native proteins. Nevertheless, comparison between predicted φ, ψ distributions and the coil library appears to be the best available option at present.
Partial Success of the ESM.
The rationale for the approach used here to predict backbone conformations is that the energy differences between backbone conformations of denatured proteins are probably small. Therefore it is desirable to calculate the relevant energy terms directly and to test them one term at a time. This approach produces partial success here: the ESM produces limited variation in g(φ) of the same type seen in the coil library. This limited success is primarily produced by the ESF term in the energy function of the ESM because, when ESF is set = 0, only a small amount of variation in g(φ) is still seen (Fig. 5A). It may be caused by use of the allowed regions in the Ramachandran maps of the amino acids.
It is a challenge now to learn whether force field simulations, based on using a comprehensive force field, can achieve better agreement than the simulations of the ESM. Our results indicate that, to make a force field succeed with denatured proteins, it should reproduce accurately the solvation energies of amides, and some force fields fail to do this (32). The OPLS–AA force field has been adjusted to take account of this problem (33), and this may be a good starting point.
Nature of the Equilibrium Between PII and β.
The g(φ) distributions of the coil library indicate that the equilibrium between PII and β is different for every amino acid type in denatured proteins. The PII to β interconversion is not a simple two-state equilibrium because the position of the β-region band varies substantially among the amino acid types, and alanine shows more than one β-region band. The energetics governing the distribution of PII and β can be analyzed by considering the individual energy terms in the ESM. The ESF and Elocal differences between φ = −70° (characteristic of PII) and φ = −120° (characteristic of β) have been calculated for the various amino acids in a simple model system (unpublished data) and will be discussed in a later publication.
Acknowledgments
We thank Jan Hermans for discussion. This work was supported by the Ministry of Education, Science, and Sport of Slovenia.
Abbreviations
- RCM
random coil model
- ESM
electrostatic screening model
- ESF
electrostatic solvation free energy
- PII
polyproline II
References
- 1.Serrano L. J Mol Biol. 1995;254:322–333. doi: 10.1006/jmbi.1995.0619. [DOI] [PubMed] [Google Scholar]
- 2.Smith L J, Fiebig K M, Schwalbe H, MacArthur M W, Thornton J M, Dobson C M. J Mol Biol. 1996;255:494–506. doi: 10.1006/jmbi.1996.0041. [DOI] [PubMed] [Google Scholar]
- 3.Karplus M. J Chem Phys. 1959;30:11–15. [Google Scholar]
- 4.Swindells M B, MacArthur M W, Thornton J M. Nat Struct Biol. 1995;2:596–603. doi: 10.1038/nsb0795-596. [DOI] [PubMed] [Google Scholar]
- 5.Flory P J. Statistical Mechanics of Chain Molecules. New York: Wiley; 1969. pp. 30–31. and 255–274. [Google Scholar]
- 6.Brant D A, Flory P J. J Am Chem Soc. 1965;87:2788–2791. [Google Scholar]
- 7.Brant D A, Flory P J. J Am Chem Soc. 1965;87:2791–2800. [Google Scholar]
- 8.Brant D A, Miller W G, Flory P J. J Mol Biol. 1967;23:47–65. [Google Scholar]
- 9.Avbelj F, Moult J. Biochemistry. 1995;34:755–764. doi: 10.1021/bi00003a008. [DOI] [PubMed] [Google Scholar]
- 10.O'Connell T M, Wang L, Tropsha A, Hermans J. Proteins. 1999;36:407–418. [PubMed] [Google Scholar]
- 11.Hu H, Elstner M, Hermans J. Proteins. 2003;50:451–463. doi: 10.1002/prot.10279. [DOI] [PubMed] [Google Scholar]
- 12.Sitkoff D, Sharp K A, Honig B. J Phys Chem. 1994;98:1978–1988. [Google Scholar]
- 13.Avbelj F, Fele L. J Mol Biol. 1998;279:665–684. doi: 10.1006/jmbi.1998.1792. [DOI] [PubMed] [Google Scholar]
- 14.Avbelj F. J Mol Biol. 2000;300:1337–1361. doi: 10.1006/jmbi.2000.3901. [DOI] [PubMed] [Google Scholar]
- 15.Avbelj F, Luo P, Baldwin R L. Proc Natl Acad Sci USA. 2000;97:10786–10791. doi: 10.1073/pnas.200343197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Avbelj F, Baldwin R L. Proc Natl Acad Sci USA. 2002;99:1309–1313. doi: 10.1073/pnas.032665499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Pappu R V, Srinivasan R, Rose G D. Proc Natl Acad Sci USA. 2000;97:12565–12570. doi: 10.1073/pnas.97.23.12565. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Pappu R V, Rose G D. Protein Sci. 2002;11:2437–2455. doi: 10.1110/ps.0217402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Ackerman M S, Shortle D. Biochemistry. 2002;41:13791–13797. doi: 10.1021/bi020511t. [DOI] [PubMed] [Google Scholar]
- 20.Dauber-Osguthorpe P, Roberts V A, Osguthorpe D J, Wolff D J, Genest M, Hagler A T. Proteins. 1988;4:31–47. doi: 10.1002/prot.340040106. [DOI] [PubMed] [Google Scholar]
- 21.Chothia C. J Mol Biol. 1976;105:1–14. doi: 10.1016/0022-2836(76)90191-1. [DOI] [PubMed] [Google Scholar]
- 22.Metropolis N, Rosenbluth A W, Rosenbluth M N, Teller M N, Teller E. J Chem Phys. 1952;21:1087–1092. [Google Scholar]
- 23.Pardi A, Billeter M, Wüthrich K. J Mol Biol. 1984;180:741–751. doi: 10.1016/0022-2836(84)90035-4. [DOI] [PubMed] [Google Scholar]
- 24.Ludvigsen S, Andersen K V, Poulsen F M. J Mol Biol. 1991;217:731–736. doi: 10.1016/0022-2836(91)90529-f. [DOI] [PubMed] [Google Scholar]
- 25.Vuister G W, Bax A. J Am Chem Soc. 1998;115:7772–7777. [Google Scholar]
- 26.Schmidt J M, Blumel M, Lohr F, Rüterjans H. J Biomol NMR. 1999;14:1–12. doi: 10.1023/A:1008345303942. [DOI] [PubMed] [Google Scholar]
- 27.Press W H, Teukolsky S A, Vetterling W T, Flannery B P. Numerical Recipes in Fortran 77: The Art of Scientific Computing. 2nd Ed. Cambridge, U.K.: Cambridge Univ. Press; 1992. [Google Scholar]
- 28.Penkett C J, Redfield C, Dodd I, Hubbard J, McBay D L, Mossakowska D E, Smith R A G, Dobson C M, Smith L J. J Mol Biol. 1997;274:152–159. doi: 10.1006/jmbi.1997.1369. [DOI] [PubMed] [Google Scholar]
- 29.Peti W, Hennig M, Smith L J, Schwalbe H. J Am Chem Soc. 2000;122:12017–12018. [Google Scholar]
- 30.Weiner S J, Kollman P A, Nguyen D T, Case D A. J Comp Chem. 1986;7:230–252. doi: 10.1002/jcc.540070216. [DOI] [PubMed] [Google Scholar]
- 31.Brooks B R, Bruccoleri R E, Olafson B D, States D J, Swaminathan S, Karplus M. J Comp Chem. 1983;4:187–217. [Google Scholar]
- 32.Marten B, Kim K, Cortis C, Friesner R A, Murphy R B, Ringnalda M N, Sitkoff D, Honig B. J Phys Chem. 1996;100:11775–11788. [Google Scholar]
- 33.Rizzo R C, Jorgensen W L. J Am Chem Soc. 1999;121:4827–4836. [Google Scholar]