Bacteria are not too small for spatial sensing of chemical gradients: An experimental evidence

Abstract

By analyzing the chemotactic behavior of a recently described marine bacterial species, we provide experimental evidence that bacteria are not too small for sensing chemical gradients spatially. The bipolar flagellated vibrioid bacteria (typical size 2 × 6 μm) exhibit a unique motility pattern as they translate along as well as rotate around their short axis, i.e., the pathways of the cell poles describe a double helix. The natural habitat of the bacteria is characterized by steep oxygen gradients where they accumulate in a band at their preferred oxygen concentration of ≈2 μM. Single cells leaving the band toward the oxic region typically return to the band within 16 s following a U-shaped track. A detailed analysis of the tracks reveals that the cells must be able to sense the oxygen gradient perpendicular to their swimming direction. Thus, they can detect oxygen gradients along a distance of ≈5 μm corresponding to the extension of their long axis. The observed behavior can be explained by the presence of two independent sensor regions at either cell pole that modulate the rotation speed of the polar flagellar bundles, i.e., the flagellar bundle at the cell pole exposed to higher oxygen concentration is rotating faster than the other bundle. A mathematical model based on these assumptions reproduces the observed swimming behavior of the bacteria.

Flagellar motility is widespread among prokaryotes living in aquatic environments, and it is estimated that 20% of marine planktonic bacteria are motile (1). Generally, bacteria exhibit motility to find places in their environment where they can maximize their substrate or energy uptake. To achieve this, they have to modulate their motility in response to environmental variables (2). When cell motility is modulated via sensing of chemical signals in the environment, the resulting motility behavior is termed chemotaxis. Best understood is the chemotactic behavior of the flagellated enteric bacterium Escherichia coli (reviewed in refs. 3–5). More or less straight swimming paths (caused by synchronous counter-clockwise rotation of all flagella) are interrupted periodically by random direction changes: so-called tumbles caused by short-term direction reversals of one or more flagella. Chemical attractants or repellants bind to specific receptor protein complexes at the cell surface, which subsequently inhibit or promote, respectively, the phosphorylation of an intracellular freely diffusing signaling protein. The flagellar motors respond to increased phosphorylation levels of the signaling protein with more frequent reversals of flagellar rotation causing more frequent tumbling of the bacteria. Additionally, a dynamic methylation of the receptor protein complexes provides an adaptation mechanism, ensuring that the chemotactic behavior is functioning over a wide range of attractant or repellant concentrations. If a bacterium experiences increasing attractant (or decreasing repellant) concentrations along its swimming path, the described mechanism results in less-frequent random direction changes. Thus, on average the cell moves toward higher attractant (or lower repellant) concentrations, exhibiting a biased random walk. Other species exhibit variations of this behavior; i.e., they show reversals of swimming direction rather than random direction changes (6). The principle of the biased random walk is predominant among free-swimming bacteria, as demonstrated, e.g., enteric (7), pelagic (6), or phototrophic (8) bacteria.

Bacteria exhibiting a biased random walk do not perform true chemotaxis, i.e., their swimming direction is not correlated with the direction of the sensed chemical gradient. True chemotaxis would be more efficient, because cells could steer directly toward attracting spots. Their effective velocity toward the attractant would be nearly as high as their swimming velocity, whereas a biased random walk maximally results in effective velocities of ≈10% of the swimming velocity (9). Although true chemotaxis is known for many free-swimming protists (10, 11), among prokaryotes it has been demonstrated only for the sulfide-oxidizing bacterium Thiovulum majus (12). This fast-swimming spherical bacterium with swimming speeds up to 600 μm⋅s⁻¹ shows a versatile motility behavior to stay at its preferred oxygen concentration of ≈10 μM within sulfide-oxygen countergradients (13, 14). Their motility can be described by a translational and a rotational component resulting in a helical pathway of the cell (except for the degenerated cases if the angle between the rotational and translational axes equals 0° or 90°). The cells sample the chemical concentration temporally along their swimming tracks. If the swimming path is not aligned with the direction of the chemical gradient, the cells will experience a periodically changing chemical concentration due to their helical pathway. True chemotaxis is realized by a mechanism termed “helical klinotaxis” (15), where a cell modulates the rotational and translational components of its helical motion in response to the periodic changing signal (12).

Both biased random walk and helical klinotaxis are based on temporal sensing, that is, at any instant the cell senses only a single integrated signal of the ambient chemical concentration. To detect a chemical gradient, the cell therefore must compare the measured signals obtained over time along its swimming track. An alternative sensing principle would be spatial sensing. In this case the cell possesses at least two independent, spatially separated sensor regions on its membrane, which would allow for measuring the direction of the chemical gradient instantly across the cell extension. The resulting motility behavior is termed “tropotaxis” (2). It was commonly assumed that prokaryotes are too small to exhibit spatial sensing of chemical gradients (16–19). A statistical analysis of chemoreception by Berg and Purcell (20) actually showed that a nonmoving E. coli cell, in principle, could be able to perform spatial sensing. But they argued that because of the absorption of the chemoattractant, the swimming cell would always sense a higher concentration at its front compared with its back, and thus spatial sensing would not be possible. Dusenbery (21) proposed that this should not be a hindrance for spatial sensing, becaue the cell could adapt to these conditions. His detailed theoretical analysis showed that the lower cell-size limit for spatial gradient sensing is actually <1 μm (21). Certain filamentous cyanobacteria are known to exhibit true phototaxis by spatially sensing the light gradient across the cells (22), but there has been no experimental evidence for spatial sensing of chemical gradients by prokaryotes.

Here we report on the chemotactic behavior of a recently described Gram-negative, vibrioid bacterium with typical cell sizes of 2 × 6 μm, which forms whitish, translucent veils on top of sulfidic marine sediment (23). The bacterium has not been isolated in pure culture, and a phylogenetic analysis is still lacking. The ecological niche of the vibrioid bacteria is characterized by oxygen-sulfide countergradients developing in and above reduced marine sediment. The bacteria exhibit swimming motility driven by two bipolar positioned flagellar bundles (see Fig. 2A). They show a pronounced chemotaxis toward an oxygen concentration of ≈2 μM, where they are able to attach themselves to solid particles with an excreted mucous thread. The cohesive threads of numerous aggregated bacteria form whitish, translucent veils positioned at the oxic–anoxic interface. The position of the veils at the oxic–anoxic interface indicates that the bacteria are microaerophilic with a yet-unresolved metabolism, probably related to the oxidation of reduced sulfur compounds with molecular oxygen. In the following, a detailed analysis of the chemotactic swimming behavior of the bacterium shows strong indications for true chemotaxis based on spatial gradient sensing of oxygen.

Figure 2.

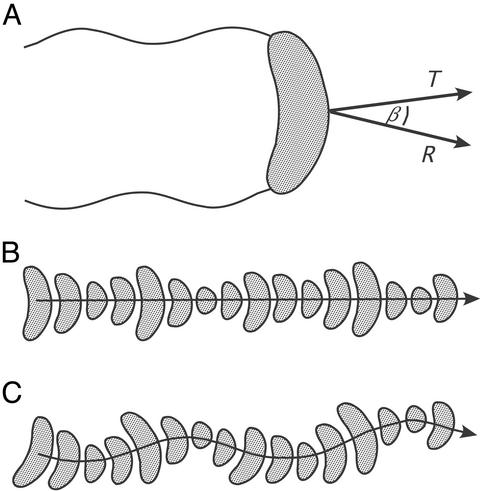
Motility behavior of the vibrioid bacteria. (A) Schematic drawing of the bipolar flagellated bacterium indicating the translation (T) and rotation axis (R) of its motility. The angle between both axes is denoted as β. (B) Two-dimensional projections of successive positions of the bacterium along its swimming path if the axes T and R are aligned (β = 0). The center of the cell follows a straight line, whereas both ends describe a helical pathway. (C) As described for B but the axes T and R are slightly diverging (β = 0), and the center of the cell follows a helical pathway.

Materials and Methods

Enrichment Culture.

Marine sulfidic sediment mixed with decaying seagrass and macroalgae was sampled from the upper 50 mm of the sediment in Nivå Bay (30 km north of Copenhagen) and filled into Petri dishes (250 mm in diameter, 150 mm in height). The Petri dishes were placed into an aquarium filled with sea water from the sampling site (15–20‰ salinity, 20°C). The sea water was flushed with air continuously, causing advective water movement with a velocity of ≈5 mm⋅s⁻¹ above the sediment surface. After 2–3 days the sediment surface was covered partially by whitish, translucent veils formed by the vibrioid bacteria. The bacteria were sampled for the experiments by collecting ≈1 × 1-mm pieces of the veils with a Pasteur pipette.

Analysis of Cell Motility.

Bacterial veil samples were transferred into flat glass capillaries (inner dimension 40 × 8 × 0.8 mm, VitroCom, Mountain Lakes, NJ) filled with filtered, oxygen-saturated sea water. The capillary was mounted horizontally on a light microscope (Labphot-2, Nikon). The focal plane was adjusted to the middle of the capillary to avoid interactions between bacteria and glass walls. Bacterial motility behavior was monitored by a charge-coupled device camera (EHDkamPro02, EHD, Damme, Germany) connected to a digital video recorder (GVD900E, Sony, Tokyo). Swimming tracks of single bacteria were obtained manually by single-step analysis of the digital video recordings. Only tracks lying completely within the focal plane were taken into account. Average swimming velocities were obtained by measuring the displacement of randomly chosen cells within time intervals of 0.48–0.96 s. Rotation speeds of the bacteria around their short axis were obtained by measuring the time interval needed for two complete rotations of randomly chosen cells.

Oxygen Microprofiles.

Dissolved oxygen measurements were done in the capillaries with Clark-type O₂ microsensors with a guard cathode (tip diameter, 10–20 μm; <1–2% stirring sensitivity) (24) connected to a picoammeter (Unisense, Århus, Denmark). A linear two-point calibration was performed from microsensor readings in sea water flushed with air and nitrogen, respectively. The microsensor was mounted on a micromanipulator (Märzhäuser, Wetzlar, Germany), and its tip was moved into the flat glass capillary. Oxygen microprofiles were recorded at 0.1-mm steps.

Numerical Calculations.

Calculations for numerically solving the differential equation and the integral of the mathematical model were performed with the software program EXCEL (Microsoft).

Results and Discussion

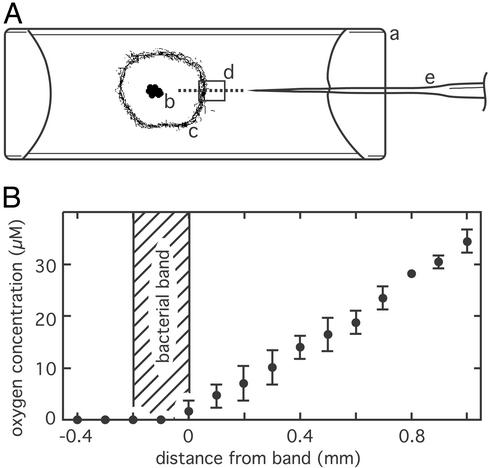
After samples of the bacterial veils had been transferred into flat glass capillaries, the region around the veil samples became anoxic within 30 min because of the respiratory activity, leading to an accumulation of the vibrioid bacteria in a circular 50- to 200-μm-thick band around the original veil sample (Fig. 1A). The bacterial bands were always positioned at the oxic–anoxic interface (Fig. 1B), whereas the band border toward the oxic region was positioned at an oxygen concentration of ≈2 μM. The almost linear oxygen gradients toward the bacterial bands had typical slopes of 30 μM⋅mm⁻¹ (Fig. 1B). Bacteria within the band were attached with their mucous stalk. Occasionally, single bacteria detached, left the band, and swam into the oxic region. However, 81% of the detached cells returned within 16 s to the band, as determined from 100 observed cells randomly chosen at ≈100 μm distance to the band.

Figure 1.

Experimental conditions for the investigation of chemotactic behavior. (A) A sample (b) of the bacterial veil from an enrichment culture was put into a flat glass capillary (a). After ≈30 min the motile bacteria aggregated in a circular band (c). Oxygen microprofiles were measured with an oxygen microsensor (e) along the dotted line. The region where the motility behavior of the bacteria was observed by light microscopy is indicated by the square (d). (B) Measured oxygen microprofile perpendicular to bacterial band (hatched region). Data points represent the mean, and error bars represent the standard deviation of two consecutive measurements.

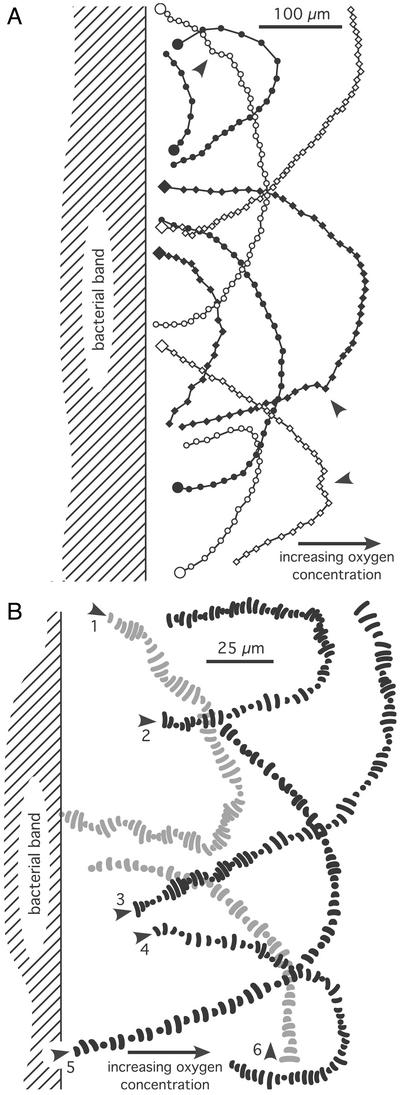
The free-swimming cells exhibited a conspicuous swimming pattern, as they translated along as well as rotated around their short axis, with the convex side of the vibrioid cell always pointing in the forward direction (Fig. 2A). If the rotation axis R and the translation axis T were aligned, both ends of the cell described a left-handed double helix along the swimming track, whereas the center followed a straight line (Fig. 2B). Occasionally, the direction of both axes deviated slightly from each other causing the center of the cell to describe a helical pathway, seen as a sinusoidal shape in the two-dimensional projection of the track (Fig. 2C). Within a single microscopic preparation the bacteria showed average swimming velocities of v₀ = 54.6 ± 9.4 μm⋅s⁻¹ for the tracks shown in Fig. 3A or 74.9 ± 10.8 μm⋅s⁻¹ for Fig. 3B (average ± standard deviation, n = 10). The difference in average swimming velocities in between different microscopic preparations was probably due to different substrate concentrations. Typical rotation frequencies of the bacteria around their short axis were 3.1 ± 0.8 s⁻¹ (average ± standard deviation, n = 10) for the tracks shown in Fig. 3B. Swimming speeds and rotation frequencies did not show any dependence on the actual position of the cells in the oxygen gradient. Thus, a purely energetic mechanism such as chemokinesis, where increased oxygen levels would increase the energy supply of the flagella resulting in higher swimming speeds, can be ruled out as the underlying chemotactic mechanism. Reversals of swimming direction were never observed, but the cells could gradually change their swimming direction resulting in smooth U-shaped tracks (Fig. 3).

Figure 3.

Observed swimming tracks from two different microscopic preparations of the vibrioid bacteria when leaving the band toward the oxic region. (A) The consecutive positions (time steps, 0.24 s) of the bacteria are indicated by dots along the tracks. Large dots mark the beginning of the tracks. Arrows indicate deviations from the overall U shape of the tracks. (B) Six different tracks at higher resolution showing the two-dimensional projections of the bacterial shape at consecutive positions (time steps, 0.04 s) along their swimming paths. Arrows indicate starting positions.

The observed chemotactic behavior might be explained by temporal gradient sensing as it was proposed for the “U-turn” response of the sulfide-oxidizing bacterium T. majus (13). According to this model, cells leaving the band experience a temporal deviation from their optimal oxygen concentration along their swimming track. If the sensed deviation rate exceeds a certain trigger value, the cells initiate a programmed U-turn response, where the cells are not influenced further by the oxygen gradient along the U-formed part of their tracks. However, this model cannot explain the motility behavior of the vibrioid bacteria: Occasionally, the swimming paths of the cells were disturbed by encounters with other cells or particles, which resulted in deviations of their swimming direction from the overall U-shaped tracks (see arrows in Fig. 3A). But within 1 s the cells corrected these deviations and resumed on their U-shaped track. In contrast to a programmed U-turn response, the cells thus were able to adjust their swimming direction continuously in response to the ambient oxygen gradient. This observation implies that the vibrioid bacteria exhibited true chemotaxis, because their swimming direction was directly correlated to the oxygen gradient. If α designates the angle between the direction of the oxygen gradient and the momentary swimming direction of the cell (Fig. 4A), then the cells always tended to increase this angle by bending their swimming path. The vibrioid bacteria apparently were able to sense the oxygen gradient laterally to their swimming path, otherwise they would not “know” in which direction to steer.

Figure 4.

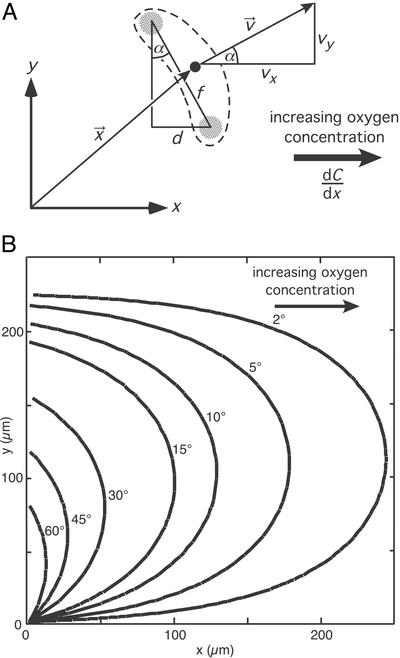
Model for the chemotactic behavior of the vibrioid bacteria. The bacterial band is positioned along the y axis (x = 0), and the homogeneous oxygen gradient dC/dx is directed along the x axis. (A) Geometric definitions for the two-dimensional mathematical model. The broken line represents the outer shape of the bacterium with a black dot marking the center and shaded regions indicating the two sensor regions. The position and orientation of the cell is given by the vector x⃗ and the angle α. The distance between the two sensor regions is given by f, whereas their distance in the x direction is denoted with d. The vector v⃗ with the Cartesian elements v_x and v_y denotes the velocity of the cell. (B) Plots of several swimming tracks obtained from the two-dimensional mathematical model. All tracks start at the origin of the coordinate system. The numbers close to the tracks represent the initial orientation α of the cells.

Bacterial swimming tracks acquired at higher spatiotemporal resolution provided more details about the underlying mechanism of the lateral gradient sensing (Fig. 3B). For some tracks (e.g., Fig. 3B, track 1) the cell center followed a helical pathway (Fig. 1C). In this case helical klinotaxis (see above) based on temporal gradient sensing could be a possible explanation, but in many cases there was no obvious helical pathway (e.g., Fig. 3B, track 5). If the cell center followed a helical pathway, then the helix diameter must have been much less than the cell extensions. Thus, the vibrioid bacteria apparently were able to sense a lateral gradient within a distance of ≈5 μm, corresponding to their lateral cell extension.

Because of the lateral symmetry of the vibrioid bacteria, one might speculate that there exist two independent sensing regions at either end of the vibrioid cells (Fig. 4A) to perform spatial sensing. Interestingly, electron microscopy of the bacteria has revealed suspicious three-layered structures at either cell pole, which might be functionally related to the sensor regions (23). Given a typical oxygen gradient of 30 μM⋅mm⁻¹, a 6-μm-long vibrioid cell would experience an oxygen concentration difference of 0.2 μM between both cell ends. Therefore, at an ambient oxygen concentration of c = 2 μM, the sensing regions must be able to sense with a precision, p, of <10%. Berg and Purcell (20) provided an estimate based on chemoattractant absorption statistics that an object of radius a could measure the ambient chemical concentration c with a maximum precision of

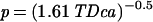(with integration time T and diffusion constant D of the chemoattractant). In our case the integration time is limited by the time period that the vibrioid bacteria need for half a rotation around their short axis, i.e., T = 0.16 s. Assuming an extension of the sensor region of a = 1 μm and a diffusion constant of D = 2 × 10⁻⁵ cm²⋅s⁻¹ for dissolved molecular oxygen (14), the maximum physically possible precision would be P = 0.13%. Thus, the bacteria indeed should be able to detect the direction of the oxygen gradients by comparing measurements of the two polar sensor regions.

Taking into account the observation that the flagella of the vibrioid bacteria never showed a reversal in rotation direction, and that otherwise a bacterium can only control the rotation speed of its flagella (4), we propose the following model explaining the observed chemotactic behavior: The ambient oxygen concentration is sensed at either end of the cell. The rotation speed of the flagella is modulated proportional to the sensed concentration difference; i.e., the flagellar bundle at the cell end toward higher oxygen concentration increases its rotation speed, whereas the flagella toward lower oxygen concentrations decrease it. The difference in rotation speed between the two flagellar bundles would enable the bacterium to bend its swimming path away from regions with increasing oxygen concentration. Given a typical curvature radius of 100 μm for the swimming tracks (Fig. 3) and a typical distance of the polar flagella of f = 5 μm (Fig. 4A), the rotation speed of the flagella has to be modulated on the order of 5%. The rotational motility component of the bacteria would additionally ensure that the cells were able to scan the oxygen gradient along all lateral directions of its swimming path, ensuring that the above-described sensing principle will function in a truly three-dimensional environment.

The conceptual model described above can be formulated in a mathematical model. For simplicity reasons and without weakening the evidence, we confine ourselves to a two-dimensional model, i.e., the rotational motility component is neglected. In the two-dimensional coordinate system the position and the orientation of a bacterium at time t can be described by the vector

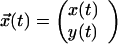and by α(t), respectively (Fig. 4A). Because the translational velocity is constant, v₀, the velocity vector is given by

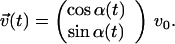1

We assume that the oxygen concentration C is increasing along the x axis, i.e., the oxygen gradient is given by dC/dx. The sensed concentration difference between the two sensor regions would be (dC/dx) f sinα(t), where f denotes the distance between the sensor regions. According to the model, the bacterium changes its orientation proportional to the sensed difference, which gives

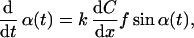2

where k is a constant. A positive value of k causes the cell to turn away from regions with increasing oxygen concentrations. Given an initial orientation α(0) = α₀, the differential equation (Eq. 2) can be solved numerically by the method after Euler–Cauchy (25). The resultant α(t) is applied to Eq. 1, which gives v⃗(t). Finally, assuming a starting position of the bacterium at the origin of the coordinate system, x⃗(t) can be obtained by numerically integrating v⃗(t) as given by x⃗(t) = ∫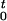v⃗(t′)dt′.

According to the experimental results the parameters were chosen as v₀ = 55 μm⋅s⁻¹, dC/dx = 30 μM⋅mm⁻¹, and f = 5 μm. The constant k influences the overall extension of the resultant tracks but not their qualitative shape. k was fitted to 300 μM⁻¹, which resulted in tracks showing similar extensions as observed in the experiments. The resultant tracks are plotted in Fig. 4B for several initial orientations α₀. The tracks show a lateral symmetry in the y direction. Bacteria starting with small orientation angles, α₀, first sense only small concentration differences between their two sensor regions. Therefore, they show a weak initial chemotactic response, causing their tracks to protrude farthest into the oxic region. The overall shape of the tracks is in good accordance with experimentally observed tracks (Fig. 3), especially the lateral symmetry in the y direction that was frequently observed. We conclude that our simple mathematical model for spatial gradient sensing provides a good simulation of the motility behavior of the vibrioid bacteria as observed under the microscope.

The proposed model with two independent sensor regions bipolar-positioned on the cell membrane is supported further by the finding that a bipolar clustering of chemotactic receptors seems to be a wide-spread feature among many phylogenetically unrelated prokaryotes (26–29). Until now, no functional relevance has been suggested for this observation, because all investigated bacteria clearly relied on chemotaxis via temporal gradient sensing. It was assumed that the signals from both receptor clusters were intracellularly integrated due to free diffusion of the signaling proteins in the cytoplasm (30). If we assume that the vibrioid bacteria also rely on freely diffusing signaling proteins, how can it be avoided that the signals from both sensor regions are integrated? In fact, Segall et al. (30) have shown for filamentous cells of E. coli (grown under addition of an antibioticum preventing cell division) that the actual range of the intracellular signal is only ≈2 μm. This unexpectedly small range was explained by a two-component signaling system. The actual signaling proteins, which are only active in their phosphorylated stage, are dynamically dephosphorylated by another freely diffusing protein in the cytoplasm (3). The dynamic deactivation provides that the chemotactic signals have a short decay time, enabling the bacteria to respond faster to changes in their chemical environment. Normally grown E. coli cells show extensions of <2 μm causing cellular integration of all receptor protein signals.

In contrast, the vibrioid bacteria show typical lengths of 6 μm. Assuming a similar two-component signaling system as in E. coli, this rather big size for a bacterium would ensure that the flagellar bundles at either end of the cell are controlled only by the local sensor regions. Within lateral oxygen gradients, each sensor region would experience a sinusoidal variation in oxygen concentration due to the rotational motility component of the bacterium. Thus, a temporal sensing mechanism responding to transient oxygen changes could ensure that the flagellar rotation speed is modulated as proposed in our model, i.e., if a sensor region senses temporally increasing oxygen levels, the rotation speed of the local flagellar bundle is increased and vice versa. The resulting sensing mechanism then would be a mixture of temporal and spatial gradient sensing. Temporal sensing would be realized at the level of a single flagellar bundle, whereas the overall chemotactic behavior of the bacterium would be characterized by the two spatially separated sensor regions. If this sensing mechanism is indeed realized by the vibrioid bacteria, the following motility behavior of cells swimming parallel to the oxygen gradient should be observed: For cells swimming upward to the gradient, both sensor regions would sense monotonously increasing oxygen levels and vice versa for cells swimming downward to the gradient. According to the proposed model, cells swimming upward to the gradient should exhibit higher swimming velocities than cells swimming downward. Because the modulation of the flagellar rotation speed is in the order of 5% (see above), the expected velocity difference should be of the same order. The spatiotemporal resolution of our bacterial tracks did not allow for detailed observation of this effect, but several tracks (e.g., Fig. 3B, tracks 2 and 4) indeed showed slightly increased swimming speeds if cells went upward to the oxygen gradient.

Our experimental results do not prove unequivocally that the chemotactic behavior of the vibrioid bacteria is based on spatial sensing. Alternatively, the observed motility behavior could be explained by a single sensor region positioned asymmetrically on the cell surface, e.g., at one end of the vibrioid cell shape. The unique motility pattern of the bacterium (Fig. 1) would cause the sensor region to follow a helical pathway, which is the necessary prerequisite for helical klinotaxis as described for the bacterium Thiovulum (12). Thus, helical klinotaxis based on temporal sensing could still be a possible explanation, but the proposed model based on spatial sensing seems more appealing, because the position of the two sensor regions close to either flagellar bundle reflects the lateral symmetry of the vibrioid bacteria. Although at this point it cannot be decided which sensing mechanism is in fact realized, our experimental results unequivocally refute the assumption that bacteria are generally too small for spatial sensing of chemical gradients. In either case (spatial sensing or helical klinotaxis based on asymmetrically positioned sensor region), the experimental observations show that the vibrioid bacteria are able to sense gradients along distances as low as 5 μm.

Dusenbery (31) has provided a detailed mathematical analysis of how different cell shapes influence the biological fitness of bacteria. The cell shapes were modeled as ellipsoids at constant volumes. Dusenbery's model assumes that bacteria use a specific amount of power for their motility and that they are influenced by drag as well as Brownian motion. The optimum values of the three main axes of the ellipsoidal cell shape were calculated to obtain the highest signal-to-noise ratio for chemical gradient detection. Chemotaxis based on temporal sensing was favored by elongated ellipsoids, i.e., rod-shaped cells, with a swimming direction along the long axis of the ellipsoid, because it is actually observed for many motile bacteria exhibiting a biased random walk. Spatial sensing of gradients directed laterally to the swimming direction was also favored by elongated ellipsoids, but now the swimming direction should be along one of the short axes of the ellipsoid. The latter is exactly the case for the motility behavior of our vibrioid bacteria. Dusenbery (21) also pointed out that spatial gradient sensing would be favored against temporal sensing in environments showing steep gradients. In fact, the natural microenvironment of the vibrioid bacteria on top of sulfidic marine sediments is characterized by extremely steep oxygen gradients showing values of up to 1 mM⋅mm⁻¹ (23).

The proposed model for the chemotactic behavior of the vibrioid bacteria is based on the modulation of flagellar rotation speed. This mechanism is in contrast to the behavior of E. coli, which relies on short-term reversals of rotation direction keeping its flagellar rotation speed rather constant. However, chemotaxis based solely on rotation speed modulation has been reported for Sinorhizobium meliloti (32), but this soil bacterium exhibits no true chemotaxis and relies clearly on temporal gradient sensing. Furthermore, the fact that the ends of the vibrioid cells traces a left-handed helix implies that the flagella rotate clockwise if seen from behind, whereas the flagella of other bacteria such as E. coli typically rotate counter-clockwise during straight swimming paths (5). However, the sulfide-oxidizing bacterium T. majus, which lives in the same environment as the vibrioid bacteria, deviates also from this general scheme by showing clockwise-rotating flagella (13).

Future studies might provide more insights into the intracellular mechanism behind the unique motility behavior of the vibrioid bacteria. It will be interesting to look for more prokaryotes with a chemotactic behavior deviating from the pure temporal sensing principle. Especially bigger species with cell extensions >5 μm seem to be good candidates, and the occurrence and behavior of such morphotypes in habitats exhibiting steep chemical gradients should be investigated in more detail. Supplemental information can be obtained at www.zi.ku.dk/mkuhl/fb.