Sexual selection affects local extinction and turnover in bird communities

Abstract

Predicting extinction risks has become a central goal for conservation and evolutionary biologists interested in population and community dynamics. Several factors have been put forward to explain risks of extinction, including ecological and life history characteristics of individuals. For instance, factors that affect the balance between natality and mortality can have profound effects on population persistence. Sexual selection has been identified as one such factor. Populations under strong sexual selection experience a number of costs ranging from increased predation and parasitism to enhanced sensitivity to environmental and demographic stochasticity. These findings have led to the prediction that local extinction rates should be higher for species/populations with intense sexual selection. We tested this prediction by analyzing the dynamics of natural bird communities at a continental scale over a period of 21 years (1975–1996), using relevant statistical tools. In agreement with the theoretical prediction, we found that sexual selection increased risks of local extinction (dichromatic birds had on average a 23% higher local extinction rate than monochromatic species). However, despite higher local extinction probabilities, the number of dichromatic species did not decrease over the period considered in this study. This pattern was caused by higher local turnover rates of dichromatic species, resulting in relatively stable communities for both groups of species. Our results suggest that these communities function as metacommunities, with frequent local extinctions followed by colonization. Anthropogenic factors impeding dispersal might therefore have a significant impact on the global persistence of sexually selected species.

One of the key assumptions of theoretical models of sexual selection is the antagonistic effect of natural and sexual selection on the evolution of exaggerated sexual advertisements (1). On one hand, competition among males and/or female preference can result in the evolution of costly sexual traits; on the other hand, extravagant ornaments can incur survival costs. As a consequence, the evolution of exaggerated displays is thought to displace individuals harboring such traits from their survival optimum (2). Survival costs of sexual displays have been shown both at the intraspecific and interspecific level. In a pioneering study, Endler (3, 4) showed that the number and size of color spots in guppies (Poecilia reticulata) were tightly linked to the distribution of predator species in the stream; the number of color spots decreased in areas with high visual predation. A laboratory study on experimental populations of guppies experiencing various predation regimes confirmed the causative link between expression of secondary sexual traits and predation (3, 4). Comparative evidence for survival costs of sexual advertisement comes from studies on birds. Using a phylogenetic framework, Promislow and coworkers (5, 6) have shown that sexual dichromatism was associated with higher mortality rate within passerines and waterfowl.

Much emphasis has been put on the consequences of this selective load on the population dynamics and the persistence of sexually selected populations/species, leading to the prediction that extinction rates should be higher for populations/species with intense sexual selection. Evidence for this prediction has been provided by independent tests of the fate of bird species introduced onto oceanic islands. Dichromatic bird species (i.e., bird species where males and females differ in color) introduced into Tahiti, Oahu (Hawaii), and New Zealand were more likely to go locally extinct compared with monochromatic species (7, 8).

If sexual selection affects extinction risk, all else being equal, one should expect that elaborate secondary sexual characters occur in clades with low species richness (because of the erosion in species number caused by extinction). However, analyses of the association between sexual dichromatism and species number have provided exactly the opposite results: dichromatism positively correlates with species richness across sister taxa of birds (9, 10). Further comparative work has emphasized the role of sexual selection on bird speciation by comparing the number of species in taxa with different mating system and ornaments (11, 12). Sexual selection could therefore promote speciation when variation in secondary sexual traits and mating preferences within a population leads to prezygotic isolation (13).

Sexual selection appears therefore to have conflicting effects on species number, promoting species formation but also potentially exposing them to higher extinction risks. According to this scenario, it might actually prove difficult to assess, on an evolutionary time scale, the relative importance of these conflicting effects on species diversity. However, over a short time scale, and in a context of large habitat deterioration caused by human activities (14), one might expect that if dichromatic species have higher extinction rates this should result in a decreasing number of such species. Estimation of extinction rates has been problematic because of confounding aspects associated with detection error and spatial autocorrelation. Here we address these issues in an empirical test of the effect of sexual selection on the local dynamics of bird communities by using data collected at a continental scale over a period of 21 years (1975–1996). In particular, we tested whether dichromatic species had higher local extinction rates compared with monochromatic birds. Moreover, because local extinction can be compensated by colonization from nearby landscapes (15, 16), we also compared turnover rates and species richness between the two groups of species.

Methods

Data.

Presence/absence data were obtained from the North American Breeding Bird Survey (BBS), a continent-wide survey of breeding birds carried out along survey routes by volunteers (17, 18). Each BBS route was considered an independent sample and consisted of 50 stops 0.8 km apart along a secondary road. At each stop one observer counted all birds seen or heard within one 3-min morning period during the breeding season. We included six orders of birds (Columbiformes, Cuculiformes, Apodiformes, Coraciiformes, Piciformes, and Passeriformes) because they are active during the day and thus include species that the BBS is designed to detect most reliably. Whether a species' plumage was sexually monochromatic (n = 185) or dichromatic (n = 153) was determined by consulting a field guide (19) and was considered dichromatic if there was any color difference between males and females (5–7, 10).

Estimation and Modeling.

Species richness of the two groups of birds was estimated by using a jackknife estimator (20) with five aggregate groups of 10 stops within each route considered sampling replicates of the bird community. This jackknife estimator is a common estimator used to take heterogeneity in detection probabilities into account when estimating population abundance (21). Estimating the number of species (species richness at a community level) is similar to estimating the number of individuals (abundance at a population level), and this jackknife estimator can be used for this purpose (20). In our case this methodology takes into account heterogeneity in detectability among species and survey routes, a problem that confounded previous analyses. In conjunction with this jackknife estimator (20), the estimators for extinction and turnover rates developed by Nichols et al. (22) can be used to study community dynamics. Specifically, to estimate probability of extinction we used equation 4 of Nichols et al.

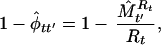where φ_tt′, is the complement of extinction probability, R_t is the number of species observed in period t, and M̂ is the estimated number of species still present at time t′ of those observed in period t. This equation defines extinction rate as the proportion of species becoming locally extinct between t and t′ (in our case, 2 successive years) among species present at period t (the first year).

To estimate turnover we used equation 7 of Nichols et al. (22)

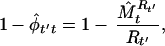which is the extinction probability estimator with data placed in reversed time order. We defined turnover rate as the proportion of new species (not present the previous year) among species present in a particular year.

Boulinier et al. (18) further explained and justified using this approach for the analysis of BBS data. We used comdyn (23), which was developed specifically for the study of community dynamics, to estimate these parameters and their associated variances. All of our analyses were based on annual rates, so that survival and extinction always refer to years t and t + 1 and turnover to years t′ and t′ − 1. As our analyses are based on estimated averages over years, subsequent use of subscripts on extinction and turnover parameters is restricted to space rather than time.

Because our interest is in evaluating the difference between extinction rates of dichromatic species and monochromatic species, it is natural to view the extinction rate estimates for a given route as paired observations, analogous to a paired t test. Thus, for each route, i, we computed the difference between dichromatic and monochromatic extinction rate estimates:

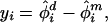where φ̂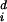 is the extinction rate for dichromatic species on survey route i and φ̂ 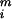is the extinction rate for monochromatic species. We then averaged the estimated differences for each route over the study period. The basic paired t test model assumes that the y_is are independent, normally distributed random variables with mean μ and variance σ². One may construct a confidence interval, or hypothesis test for μ, thus assessing whether the average difference is 0.

However, unlike more traditional applications of the paired t test, the differences are not likely to be independent because of their spatial proximity. That is, observations near one another in space are likely to be more similar than observations far apart. To yield proper statistical inferences, it is important to accommodate this spatial dependence. In addition, introduction of spatial correlation into the problem allows us to provide a general spatially explicit characterization of the difference in extinction rate without having to resort to various subjective stratification schemes, which imply very restrictive forms of spatial dependence (independence within strata, and independence of stratum effects).

To accommodate spatial dependence, we introduce an additional error term into the model, which we assume to be spatially correlated. Our model is thus:

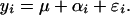As in the usual paired t test setting, the ɛ_is are assumed to be normally distributed random variables with mean 0 and variance σ², μ is the mean difference, as before, and the additional error terms α_i are assumed to be correlated random variables. Because routes have been sampled for different numbers of years, we introduce the added structure that the variance of ɛ_i is σ²/N_i, where N_i is the number of years of data from route i, thus acknowledging the varying precision with which route-specific differences are estimated (this is analogous to a weighted least-squares formulation of regression problems).

This model is that used in traditional kriging applications (24) where α_i are normal (0, σ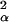), with some correlation function r(i, i′), depending on the distance between sample locations (i, i′). We chose to use the convolution approach suggested by Higdon (25) and Higdon et al. (26) to treat this spatial dependence. This approach is more amenable to the analysis of large data sets (we have >4,000 observations) and is very convenient for formal statistical inference as the basic model is a linear mixed model. We adopt a Bayesian formulation of the problem to more properly characterize prediction uncertainty (27).

Our goal is to estimate μ and quantify its variance and produce predictions of y_i, and their variances, over the BBS sampling range. It may be that the data indicate the absence of spatial correlation. Consequently, we considered a reduced model, that is without the correlated error term (this would be the usual paired t test problem), and compared the models by using an analog of Akaike's Information Criterion, known as Deviance Information Criterion, based on the model deviance and estimated complexity, or effective number of degrees of freedom (28, 29). The analyses for turnover rate were analogous to those for extinction rate.

Because there are a number of possible confounding variables associated with dichromatism, we further examined a number of these variables that were readily available (17, 19). Because larger species are known to have higher survival rates but lower population sizes, factors likely to reduce and increase extinction risk, respectively, we examine average body size (weight) to test whether dichromatic species tended to be larger or smaller than monochromatic ones. We also tested for differences in the proportion of resident, short-distance, and long-distance migrants between the two groups. Finally, we tested for any difference between the proportion of dichromatic and monochromatic species classified by a number of habitat and nesting factors, namely whether a species was a cup or cavity nester, whether a species was a ground or canopy nester, and by species-specific preferred breeding habitat (wetland, scrub land, woodland, or urban).

Results

Extinction Rate.

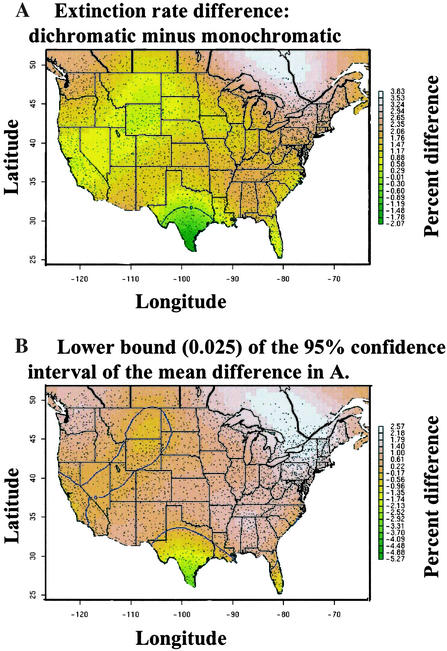
Dichromatic species had on average a 23% higher annual local extinction rate per survey route (0.079, SÊ 0.001) than monochromatic species (0.064, SÊ 0.001) with a mean difference of 0.015 and a 95% posterior interval for this difference of 0.013, 0.016. This narrow confidence interval, located far from zero, indicates a general tendency for dichromatic extinction rates to be higher than monochromatic extinction rates. This result was widespread across the continent and suggests that sexual selection influences the communities of birds in many different habitats and places. However, upon closer examination we found that a spatial model fit the data better than a model without a spatial component (ΔDIC = 117), indicating that the omnibus statement that dichromatic species have higher local extinction rates should be qualified by where the dichromatic extinction rate is greater than the monochromatic rate. We used the spatial model to compute a prediction interval of the difference between dichromatic and monochromatic extinction rates on a fine grid of points over the study region (Fig. 1A). Fig. 1B shows the lower 0.025 percentile of this estimate and illustrates regions of nonsignificance (e.g., where the difference between dichromatic and monochromatic rates is not significantly different from 0, dark green in color). The posterior mean of the proportion of area over which dichromatic extinction rate is greater than monochromatic extinction rate is 0.961 (95% posterior interval: 0.917–0.983). However the lower bound of the 95% prediction intervals (Fig. 1B) suggests that the extinction rate difference is not large in some regions (indicated by the 0 contour line), most notably in southern Texas as well as the prairie pothole region of north-central North America. Southern Texas is one area in the United States in which tropical species are present. Southern Texas and the prairie pothole region are also important components of large migratory flyways, which could possibly account for lower local extinction rates caused by increased rescue effects (15).

Figure 1.

The estimated mean difference between dichromatic and monochromatic extinction rates (A) and the lower 95% confidence interval around the mean (B). The area in which this difference is <0 is delineated by the blue contour line and is green in color. The small black dots represent North American BBS routes.

Turnover Rate.

If extinction rates are higher in dichromatic species and local communities were functioning as independent units, then some might expect the number of dichromatic species to decrease over time at a higher rate than monochromatic species. In fact, we found that the number of species in both groups increased over the time period (4.8% and 3.4%, respectively). Local species turnover rates were of the same magnitude as local extinction rates, suggesting that dispersal from other areas may play an important role in metacommunity dynamics (30, 31).

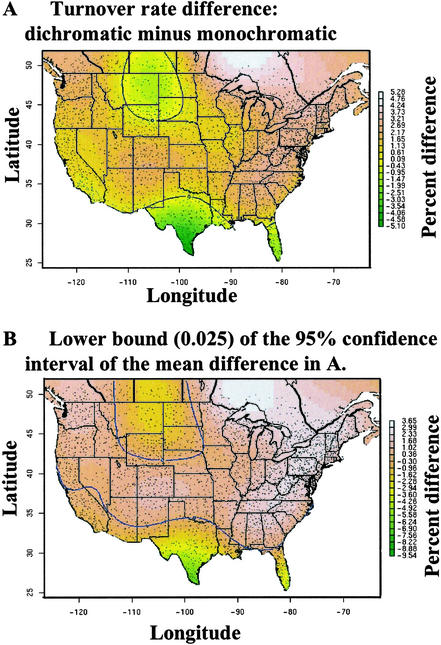
Specifically, we found local species turnover rate to be 25% higher for dichromatic (0.076 SÊ 0.001) than for monochromatic (0.061 SÊ 0.001) species with a mean difference of 0.015 and a 95% posterior interval of this difference being 0.014, 0.017. Similar to the extinction results, a spatial model fit the data more parsimoniously (ΔDIC = 268) and showed a very similar pattern to the map of extinction rate (Fig. 2) with areas of nonsignificance being southern Texas, the prairie potholes and extending to southern California (green in color). The proportion of area over which the difference was >0 was 0.841 (95% posterior interval 0.802, 0.884), which was slightly less than for extinction. By comparing Figs. 1A and 2A the spatial congruence between extinction and turnover can be seen.

Figure 2.

The estimated mean difference between dichromatic and monochromatic turnover rates (A) and the lower 95% confidence interval around the mean (B). The area in which this difference is <0 is delineated by the blue contour line and is green in color. The small black dots represent North American BBS routes.

Possible Confounding Factors.

Our modeling effort corrected for differences in detection probabilities. Estimated detection probabilities (number of species detected per number of species estimated present) did vary widely and ranged from 0.391 to 0.966 for dichromatic species and from 0.431 to 0.978 for monochromatic species.

Further, we found no difference in the proportion of birds <10 g, between 10 and 100 g, and >100 g in the two groups of birds (χ² < 0.01, 2 df, P > 0.99). We found no difference in the proportion of resident, short-distance, and long-distance migrants (χ² = 0.03, 2 df, P = 0.86). Finally, we could not find any difference between the proportion of dichromatic or monochromatic species that were cup or cavity nesters (χ² = 0.99, 1 df, P = 0.32) or were ground or canopy nesters (χ² = 0.20, 1 df, P = 0.65) or by preferred breeding-habitat (wetland, scrub land, woodland, urban; χ² = 0.89, 2 df, P = 0.82).

Discussion

We have shown that sexual dichromatism, a trait linked to the intensity of sexual selection in birds (1), affects community parameters over a large geographic area. In particular, we found that dichromatic species had significantly higher chances of becoming locally extinct compared with monochromatic birds. Surprisingly, however, this pattern did not negatively affect dichromatic species richness because local turnover rate was also significantly higher for dichromatic species.

Why should sexually selected species be more prone to local extinction? There exist several putative costs of sexual selection dealing with ecological [increased risk of predation (3, 4) and parasitism (32, 33)] and genetic [reduced effective population size because of reproductive skew (34), antagonistic coevolution between sexes (35), tradeoffs between the size of sexual traits, and the size of other morphological characters (36)] factors. Theoretical work has shown that, in a changing environment, costs of sexual selection can incur an extra selective load on populations and if there is a strong female preference this could lead to population extinction (37).

Whatever the mechanism responsible for the local extinction of sexually selected species, our results suggest that dispersal between sites, allowing high turnover, might be crucial for the population persistence of dichromatic species at the metacommunity level.

One important methodological problem faced when comparing rates of change of communities is that the probability of detecting a species may vary among species, time periods, and areas, and this could confound parameter estimates (18, 22, 31). For instance, detection probabilities of dichromatic and monochromatic species could be expected to vary because of differences in colors, song calls, or other characteristics. In fact, detection probabilities did vary widely in our data set. We were not able to handle simultaneously detection probabilities and phylogenetic effects by using modern statistical tools (38), because we estimated community-level parameters and we could not assign species-specific extinction rates. Although it is possible to estimate what proportion of a group of monochromatic or dichromatic species is not detected, it is not possible to determine which particular species are not detected.

Although we examined a number of possibly confounding factors, there still could be other characteristics that could confound our results. Species were classified as monochromatic versus dichromatic based on characteristics reported in field guides, but we acknowledge that coloration in the UV is important in the context of sexual selection because some species that do not appear as dichromatic in the visible part of the spectrum may appear dichromatic in the UV (39). As more UV-related dichromatism is described, this should be considered in future analyses, although in our case, estimates are probably conservative because any misclassification would most likely make it harder for us to detect the predicted direction of difference. Despite such variation in traits mentioned above, our predicted pattern was found in a wide array of locations and communities across the North American continent.

Our results have wide implications for the structuring of communities (40) as well as the conservation of sexually selected species. The fact that there are both higher local extinction and turnover rates for dichromatic versus monochromatic species and that there is spatial structure in these rates further suggests that these communities function as metacommunities (30), with frequent local extinction followed by recolonization. This may suggest that communities in different landscapes are highly interconnected (41, 42) and that species with particular characteristics such as dichromatism depend more heavily than others on dispersal and recolonization for their local dynamics. Environmental changes that limit dispersal effectiveness may have dramatic effects for the conservation of species of concern (31, 43). If these changes affect turnover rates negatively, multiple local extinctions could possibly lead to global extinction (44).

Abbreviation

BBS

Breeding Bird Survey