Abstract
Nonlinear mixed-effects analysis of serial sputum colony-counting data supports the existence of two bacillary subpopulations in sputum, eliminated at different rates. It distinguishes between combination regimens, removes bias, and greatly improves precision, with significant implications for the analysis of surrogate endpoints of “sterilization” in the development of new antituberculosis regimens.
Improving tuberculosis treatment depends on enhancing the “sterilizing” activity of drug regimens, and surrogate endpoints of this activity are urgently needed (9). Serial sputum colony counting (SSCC) of Mycobacterium tuberculosis early in therapy has been advocated for this purpose. “Early-bactericidal-activity” studies measure the effects of single agents over the first 2 days (10, 20), probably reflecting activity against actively dividing bacilli within cavities rather than “sterilizing” activity. Extending the sampling period could provide such a measure (11), but prolonged monotherapy raises ethical concerns. The only SSCC study employing a modern combination regimen and methods without decontamination of sputum was performed in Kenya in 1989 and 1990 (2). Reanalysis of this study (1) using summary measures (SM) (13) supports the concept of extended sampling but does not make optimal use of the data. We describe a nonlinear mixed-effects (NLME) approach offering greater efficiency.
The study design and conduct were described previously (2). A total of 122 new pulmonary-tuberculosis patients received streptomycin and isoniazid and either thiacetazone (the SHT regimen) or rifampin and pyrazinamide (the SHRZ regimen). All harbored drug-sensitive strains and consented to human immunodeficiency virus (HIV) serology (29% seropositive). Sputa were sampled for SSCC on days 0, 2, 7, 14, and 28.
The nlme package (18) in R (19) was used for NLME analysis with monoexponential and biexponential models. Only positive results were included, as in the previous analysis (1). A log10 transformation of the response and a variance function were used to account for heteroscedasticity. With an exponentiated parameterization to enforce positivity of the parameters (5), the biexponential model has the following form:
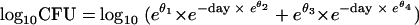 |
Fitted models were compared using the Akaike information criterion, the likelihood ratio test, and residual plots. For comparability, parameter estimates were reexpressed as intercepts A and B (θ1 and θ3 divided by 2.303) and rate constants α and β [e.g., 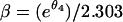 ] on the log10 scale (1). An analytical approximation,
] on the log10 scale (1). An analytical approximation, 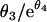 , was used to compute the elimination times of subpopulations. A linear model was used for covariate effects on the intercepts. Inferences relied on Wald tests, but other methods were used to explore and confirm the findings (quantile-quantile plots and the Shapiro-Wilks W test for normality, unpaired Student or Welch t tests, and Wilcoxon and Mann-Whitney rank sum U tests for tests of significance, as appropriate).
, was used to compute the elimination times of subpopulations. A linear model was used for covariate effects on the intercepts. Inferences relied on Wald tests, but other methods were used to explore and confirm the findings (quantile-quantile plots and the Shapiro-Wilks W test for normality, unpaired Student or Welch t tests, and Wilcoxon and Mann-Whitney rank sum U tests for tests of significance, as appropriate).
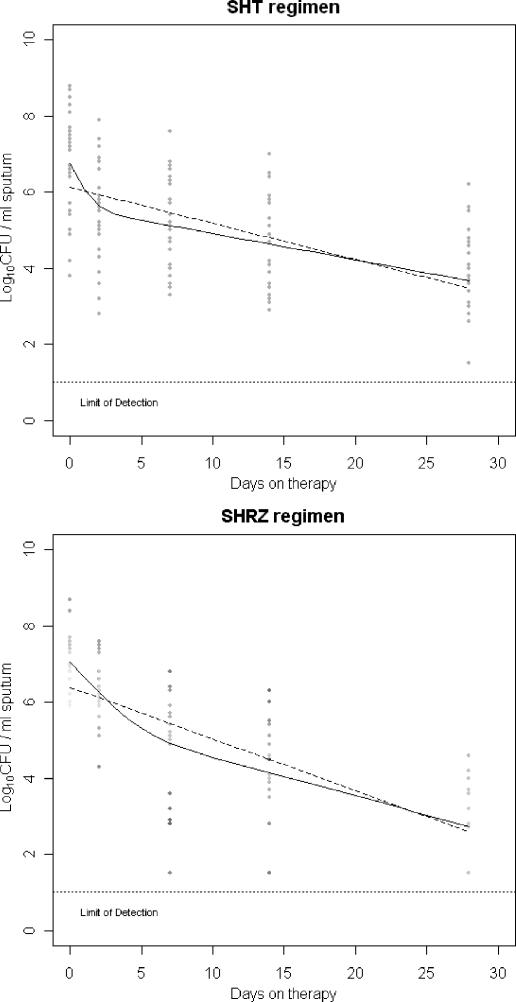
One hundred subjects (54 SHT; 46 SHRZ) had more than one data point available, and 48 subjects had five positive data points. For both data sets, model fitting unequivocally selected a biexponential model (Table 1 and Fig. 1), suggesting that at least two subpopulations of bacilli, eliminated at different rates, are present in sputum (referred to henceforth as “fast” and “slow”). Parameter estimates were consistent with previous SM estimates (1) and the effects of these regimens in clinical trials (7), with the “slow” rate constant, β, larger for SHRZ than for SHT (0.094 versus 0.063 log CFU/ml/day for regimen contrast within the whole data set [P = 0.013]; 0.094 versus 0.076 log CFU/ml/day for fitted data by regimen [P < 0.001]). The addition of random effects significantly improved the fit (P < 0.001) (Table 1), accounting for high variability in parameters between subjects, greater in the intercepts A and B than the rate constants α and β.
TABLE 1.
Point estimates and 95% confidence intervals of the fixed effects and goodness of fit for the two regimens from pooled and mixed-effects fits using the whole data set (SHT n = 54, SHRZ n = 46)
| Regimen | A (log10 CFU) | α (log10 CFU/ml/day) | B (log10 CFU) | β (log10 CFU/ml/day) | AICa | LRb test |
|---|---|---|---|---|---|---|
| SHT | ||||||
| Monoexponential | 6.081 (5.851-6.311)c | 0.102 (0.086-0.122) | 769.4 | |||
| Biexponential | 6.633 (6.282-6.984) | 0.621 (0.241-1.132) | 5.380 (4.916-5.844) | 0.066 (0.045-0.099) | 751.9 | <0.0001 |
| Biexponential mixed effects | 6.650 (6.264-7.037) | 0.881 (0.651-1.191) | 5.463 (5.114-5.812) | 0.076 (0.060-0.095) | 688.6 | <0.001 |
| SHRZ | ||||||
| Monoexponential | 6.397 (6.148-6.647) | 0.146 (0.128-0.167) | 622.2 | |||
| Biexponential | 6.845 (6.509-7.180) | 0.456 (0.243-0.858) | 5.472 (4.868-6.075) | 0.100 (0.072-0.140) | 606.4 | <0.0001 |
| Biexponential mixed effects | 6.834 (6.509-7.159) | 0.519 (0.409-0.658) | 5.307 (4.824-5.790) | 0.094 (0.079-0.113) | 526.7 | <0.001 |
AIC, Akaike information criterion.
LR, likelihood ratio.
Values in parentheses are 95% confidence intervals.
FIG. 1.
Locations of the monoexponential (dashed lines) and biexponential (solid lines) regression functions fitted to the subsets of complete profiles for the SHT (n = 29) and SHRZ (n = 19) regimens.
Differences in the A intercept by HIV status were confounded by the extent of cavitation (P = 0.432 for HIV and 0.018 for the cavitation score), but controlling for this, the B intercept remained reduced in the HIV-positive group (P = 0.008). β did not differ by HIV status for either regimen (SHT, P = 0.928; SHRZ, P = 0.367). For the SHT and SHRZ regimens, the predicted elimination times were 7.5 (5.6 to 9.5) and 13.2 (10.3 to 16.0) days for the “fast” subpopulation and 74.3 (68.8 to 79.8) and 56.2 (52.9 to 59.5) days for the “slow” subpopulation.
We compared the NLME estimates of β with different SM estimates, with respect to bias (Table 2) and precision (Table 3). Any SM estimator involving day 2 overestimated β by 16 to 139%, reflecting the persistence of the “fast” component within the first week, but over later periods agreed to within 5 to 29%. Overall, comparing the SM β (2 to 28) coefficient with NLME estimates of β, the percent coefficient of variation was reduced sixfold, from 62% to under 10%.
TABLE 2.
Bias: magnitude of SM and NLME estimators of β and their ratioa
| Parameterb | SHRZ
|
SHT
|
||
|---|---|---|---|---|
| Value (log10 CFU/ml/day) | Ratio | Value (log10 CFU/ml/day) | Ratio | |
| KI(2-7) | 0.225 | 2.39 | 0.121 | 1.61 |
| KI(2-28) | 0.115 | 1.22 | 0.060 | 0.80 |
| β(2-28) | 0.109 | 1.16 | 0.057 | 0.76 |
| KI(7-14) | 0.099 | 1.05 | 0.091 | 1.21 |
| KI(14-28) | 0.099 | 1.05 | 0.053 | 0.71 |
| NLME β | 0.094 | 1.00 | 0.075 | 1.00 |
Methods for the SM estimates are given in reference 1.
β(a-b) refers to the coefficient of a linear regression fitted to all the data points between and including times a and b. KI(a-b) refers to the slope of a straight line connecting data points at time a and b.
TABLE 3.
Precision: standard errors and percent coefficients of variation of SM and NLME estimators of β
| Parameter | Point estimate (log10 CFU/ml/day) | Standard errora | CV%b |
|---|---|---|---|
| Pooled SM β(2-28) | 0.077 | 0.048 | 62.3 |
| SHT | |||
| Complete profiles β | 0.069 | 0.014-0.017 | 20.2-25.2 |
| All data β | 0.066 | 0.012-0.015 | 18.4-22.5 |
| Mixed effects β | 0.076 | 0.008-0.010 | 10.9-12.6 |
| SHRZ | |||
| Complete profiles β | 0.100 | 0.022-0.027 | 21.4-27.3 |
| All data β | 0.100 | 0.016-0.019 | 15.7-18.6 |
| Mixed effects β | 0.094 | 0.008-0.009 | 8.8-9.7 |
A range of standard errors is given, since the confidence intervals on the log10 scale derived from NLME analysis were obtained by an exponential transformation of the confidence interval for the original parameter θ4 and hence are asymmetrical.
CV%, percent coefficient of variation.
We conclude that a biexponential model fits the data best, a finding consistent with the presence of multiple bacillary subpopulations. Alternative explanations, such as selection of drug-tolerant bacilli from an initially homogeneous population during therapy, seem less plausible given the spatial compartmentalization of bacilli in pulmonary tuberculosis (4, 6), the pharmacodynamic properties of combination chemotherapy (14, 15), and the conditions for induction of drug tolerance in vitro (16). Some studies have reported only a single population in their data (8, 12, 21) but invariably employed sputum decontamination, presumably selectively eliminating any “fast” subpopulation to various extents (3). Since the only observed population then declines at a constant rate, these data support the hypothesis of multiple baseline subpopulations.
Since the biexponential model better represents the data, it can eliminate bias in SM estimates computed over periods prior to elimination of the “fast” subpopulation. It can in principle discriminate between effects on subpopulations, a critical methodological issue for accurate estimation of “sterilizing” activity. The activities of antituberculosis drugs against different subpopulations vary in vitro (17). Agents active against multiple subpopulations or interacting pharmacodynamically with other components of a regimen in vivo could create unpredictable bias in SM estimates.
The estimated elimination times of the “slow” component raise the question of whether this subpopulation is the one from which relapses subsequently arise and therefore an appropriate model for ultimate sterilization and cure. A third subpopulation at an abundance below 10 to 103 CFU/ml of sputum may not be detected by SSCC (3), and a lack of degrees of freedom restricts the complexity of the models fitted here. Our findings need to be supported and extended by further experimental work and clinical trials. Though SSCC parameters have greater prima facie plausibility than early-bactericidal-activity measures, whether they accurately reflect clinical endpoints of “sterilization,” like relapse, requires ongoing evaluation.
NLME analysis can explicitly model complicated error structures, account for interindividual variability, and make efficient use of incomplete data. It may be a useful method of reducing bias and improving precision in assessment of the “sterilizing” activities of antituberculosis regimens.
Acknowledgments
G. R. Davies is supported by a Wellcome Trust Training Fellowship in Clinical Tropical Medicine (grant no. GR067910MA).
We thank Denis Mitchison for his foundational work in this area and for his comments on earlier drafts of this paper and Kasia Stepniewska for useful discussions regarding the statistical methods.
REFERENCES
- 1.Brindle, R., J. Odhiambo, and D. A. Mitchison. 2001. Serial counts of Mycobacterium tuberculosis in sputum as surrogate markers of the sterilizing activity of rifampicin and pyrazinamide in treating pulmonary tuberculosis. BMC Pulm. Med. 1:2-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Brindle, R. J., P. P. Nunn, W. Githui, B. W. Allen, S. Gathua, and P. Waiyaki. 1993. Quantitative bacillary response to treatment in HIV-associated pulmonary tuberculosis. Am. Rev. Respir. Dis. 147:958-961. [DOI] [PubMed] [Google Scholar]
- 3.Burdz, T. V. N., J. Wolfe, and A. Kabani. 2003. Evaluation of sputum decontamination methods for Mycobacterium tuberculosis using viable colony counts and flow cytometry. Diagn. Microbiol. Infect. Dis. 47:503-509. [DOI] [PubMed] [Google Scholar]
- 4.Canetti, G. 1955. The tubercle bacillus in the pulmonary lesion of man: histobacteriology and its bearing on the therapy of pulmonary tuberculosis. Springer Verlag, New York, N.Y.
- 5.Davidian, M., and D. M. Giltinan. 1995. Non-linear models for repeated measurement data. Chapman Hall, London, United Kingdom.
- 6.Fenhalls, G., L. Stevens-Muller, R. Warren, N. Carroll, J. Bezuidenhout, P. Van Helden, and P. Bardin. 2002. Localisation of mycobacterial DNA and mRNA in human tuberculous granulomas. J. Microbiol. Methods 51:197-208. [DOI] [PubMed] [Google Scholar]
- 7.Fox, W., G. A. Ellard, and D. A. Mitchison. 1999. Studies on the treatment of tuberculosis undertaken by the British Medical Research Council Tuberculosis Units 1946-1986, with subsequent relevant publications. Int. J. Tuberc. Lung Dis. 3:S231-S279. [PubMed] [Google Scholar]
- 8.Gillespie, S. H., R. D. Gosling, and B. M. Charalambous. 2002. A reiterative method for calculating the early bactericidal activity of antituberculosis drugs. Am. J. Respir. Crit. Care Med. 166:31-35. [DOI] [PubMed] [Google Scholar]
- 9.Global Alliance for TB Drug Development. 2001. Scientific blueprint for tuberculosis drug development. Tuberculosis (Edinburgh) 81:Suppl. 1. [DOI] [PubMed]
- 10.Jindani, A., V. R. Aber, E. A. Edwards, and D. A. Mitchison. 1980. The early bactericidal activity of drugs in patients with pulmonary tuberculosis. Am. Rev. Respir. Dis. 121:939-949. [DOI] [PubMed] [Google Scholar]
- 11.Jindani, A., C. J. Dore, and D. A. Mitchison. 2003. Bactericidal and sterilizing activities of antituberculosis drugs during the first 14 days. Am. J. Respir. Crit. Care Med. 167:1348-1354. [DOI] [PubMed] [Google Scholar]
- 12.Joloba, M. L., J. L. Johnson, A. Namale, A. Morrisey, A. E. Asseghai, R. D. Mugerwa, J. J. Ellner, and K. D. Eisenach. 2000. Quantitative sputum bacillary load during rifampicin-containing short course chemotherapy in human immunodeficiency virus-infected and non-infected adults with pulmonary tuberculosis. Int. J. Tuberc. Lung Dis. 5:528-536. [PubMed] [Google Scholar]
- 13.Matthews, J. N. S., D. G. Altman, M. J. Campbell, and P. Royston. 1990. Analysis of serial measurements in medical research. Br. Med. J. 300:230-235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Mitchison, D. A. 1985. The action of anti-tuberculosis drugs in short-course chemotherapy. Tubercle 66:219-225. [DOI] [PubMed] [Google Scholar]
- 15.Mitchison, D. A. 1998. How drug resistance emerges as a result of poor compliance during short course chemotherapy for tuberculosis. Int. J. Tuberc. Lung Dis. 2:10-15. [PubMed] [Google Scholar]
- 16.Mitchison, D. A., and A. R. M. Coates. 2004. Predictive in vitro models of the sterilizing activity of anti-tuberculosis drugs. Curr. Pharm. Des. 10:3285-3295. [DOI] [PubMed] [Google Scholar]
- 17.Paramasivan, C. N., S. Sulochana, G. Kubendiran, P. Venkatesan, and D. A. Mitchison. 2005. Bactericidal action of gatifloxacin, rifampin, and isoniazid on logarithmic- and stationary-phase cultures of Mycobacterium tuberculosis. Antimicrob. Agents Chemother. 49:627-631. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Pinheiro, J. C., and D. M. Bates. 2000. Mixed-effects models in S and S-Plus. Springer Verlag, New York, N.Y.
- 19.R Development Core Team. 2004. R: a language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. http://www.R-project.org. [Online.]
- 20.Sirgel, F. A., P. R. Donald, J. Odhiambo, W. Githui, K. C. Umapathy, C. N. Paramasivan, C. M. Tam, K. M. Kam, C. W. Lam, K. M. Sole, and D. A. Mitchison. 2000. A multicentre study of the early bactericidal activity of anti-tuberculosis drugs. J. Antimicrob. Chemother. 45:859-870. [DOI] [PubMed] [Google Scholar]
- 21.Wallis, R. S., S. A. Vinhas, J. L. Johnson, F. C. Ribeiro, M. Palaci, R. L. Peres, R. T. Sa, R. Dietze, A. Chiunda, K. Eisenach, and J. J. Ellner. 2003. Whole blood bactericidal activity during treatment of pulmonary tuberculosis. J. Infect. Dis. 187:270-278. [DOI] [PubMed] [Google Scholar]