Different time courses for visual perception and action priming

Abstract

Visual stimuli may remain invisible but nevertheless produce strong and reliable effects on subsequent actions. How well features of a masked prime are perceived depends crucially on its physical parameters and those of the mask. We manipulated the visibility of masked stimuli and contrasted it with their influence on the speed of motor actions, comparing the temporal dynamics of visual awareness in metacontrast masking with that of action priming under the same conditions. We observed priming with identical time course for reportable and invisible prime stimuli, despite qualitative changes in the masking time course. Our findings indicate that experimental variations that modify the subjective visual experience of masked stimuli have no effect on motor effects of those stimuli in early processing. We propose a model that provides a quantitative account of priming effects on response speed and accuracy.

Objects that have been encountered briefly before are recognized better and acted on faster, a phenomenon called priming (1, 2). Priming may occur without awareness of the prime, as has been shown in neurological patients (3–5) and healthy subjects (6–10). This raises the question of how the priming potential of a stimulus is related to its phenomenal experience. When the visibility of a stimulus changes, does the degree to which it primes overt behavior change in the same way? We addressed this question by using metacontrast masking, a type of backward masking in which the visibility of a briefly flashed stimulus is reduced if it is followed by a spatially flanking stimulus. There are two advantages of metacontrast masking as an experimental tool: (i) the temporal dynamics of the conscious percept and its dependence on stimulus conditions are well known (11); (ii) metacontrast-masked stimuli, even if not consciously perceived, can influence responses to the masking stimulus. First, simple reactions to the mask are speeded up by undetected primes (12). Second, unrecognized primes facilitate or inhibit choice reactions to the mask if prime and mask share stimulus attributes critical for the correct or the alternative response (6, 13).

In the experiments reported here, we measured the amount of priming from metacontrast-masked stimuli while manipulating the temporal dynamics of conscious perception. Over a wide range of time courses, we show that conscious perception and unconscious behavioral effects of masked visual stimuli obey different temporal laws.

Experiment 1

The aim of experiment 1 was to study response priming and its time course when masking is complete. Obviously, the demonstration of nonzero priming effects from nonreportable stimuli bears on the issue of subliminal perception (10, 14, 15).

Masking and priming were studied in tasks that differed only with respect to which stimulus serves as target, keeping stimulus conditions identical. On each trial, a small arrow (“prime”) was briefly presented, followed by a masking stimulus (“mask”) shaped as a large arrow. To assess perceptual masking, subjects had to report the orientation of the prime stimulus. The time course of masking was determined by measuring prime recognition across a range of stimulus-onset asynchronies (SOA) (Fig. 1a). Priming was studied by choice responses to the orientation of the mask. Whether the primes affect these responses was assessed by the effect of prime-mask congruency on response time (RT). Prime and mask are congruent if they have identical orientation and incongruent otherwise. The amount of priming was determined by the RT advantage on congruent as compared with incongruent trials. We measured priming effects across an SOA range for which the masking time course is flat and at chance level. To check on the generality of the findings, variants of the basic tasks were also performed.

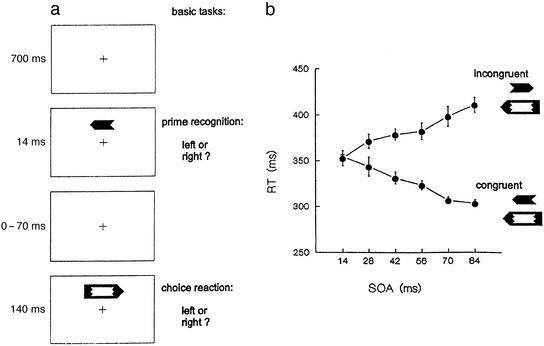
Figure 1.

(a) Temporal sequence of a typical experimental trial. Arrows oriented left or right served as prime and mask stimuli; primes subtended visual angles of 0.8° × 1.86°, masks 1.09° × 3.47°. Orientation of prime and mask varied unpredictably from trial to trial. (b) Effects of congruent and incongruent primes on choice RT as a function of SOA, in the first session of Experiment 1. Error bars indicate ± SE around means.

Method.

Subjects.

Six students from Braunschweig University, age 20–42 years, were tested in nine 1-h sessions each.

Stimuli.

Left and right arrows served as prime and mask stimuli (Fig. 1). In addition, neutral mask stimuli were used. Stimuli were presented black on white, on a 70-Hz Atari (Sunnyvale, CA) SM 124 monitor. To enhance perceptual masking, they were randomly positioned 1.38° above or below the fixation cross. The outer contour of the prime stimuli touched the inner contour of the central cutout of the masks. Prime duration was 14 ms, mask duration 140 ms. Prime-mask SOA varied randomly from trial to trial, in steps of 14 ms, from 14 to 70 ms in tasks b, c, and d, and from 14 to 84 ms in tasks a and e (see below).

Design.

Perceptual and behavioral effects of prime stimuli were assessed by both direct and indirect tasks (15). Direct tasks tested how well subjects could detect or recognize the prime stimulus. Indirect tasks assessed the effects of primes on response speed to the mask. Direct and indirect tasks were administered in the following sequence:

(a) Choice RT only (session 1; 612 trials). Subjects were instructed to respond quickly and accurately to the orientation of the mask.

(b) Choice RT and detection combined (sessions 2 + 3; 1,224 trials). On each trial, subjects reacted to mask orientation and also decided whether they had detected a prime. Detection responses were to be given without speed stress, with a delay of at least 250 ms from the choice response. Primes were present on five of six of the trials.

(c) Simple RT and recognition combined (sessions 4 + 5; 1,512 trials). Subjects gave a fast reaction to the mask onset with both hands simultaneously and after a delay of 600 ms reported prime orientation. Left, right, and neutral masks (with rectangular outer contour) occurred equally often; mask type either varied randomly or was kept constant within blocks.

(d) Recognition only (sessions 6 + 7; 1,512 trials). Subjects reported the prime orientation, disregarding the mask shape (left, right, or neutral). To prevent indirect priming effects on recognition, subjects were to respond at least 600 ms after the mask. Given that speed stress invariably reduces response accuracy (16), delayed responding should also provide optimal conditions for recognition performance (13). Other details are as in c.

(e) Choice RT only (session 9; 612 trials). Instruction as in a. Prime and mask appeared at the center of the screen in half of the trials, above or below fixation in the remaining trials.

Procedure.

Trials started with a fixation cross, followed after 700 ms by the prime either above or below, and the mask at the same position (except in e). Responses were given by pressing a response button with the left or right index finger. Visual feedback was provided on choice RT error trials. To avoid perceptual interference, error feedback was acoustic in recognition. Trials were grouped in blocks of 50–72 trials, and summary feedback (mean RT, percentage correct) was given after each block. Subjects were first informed about the existence of prime stimuli in session 2.

Statistical methods.

Detection and recognition performance was analyzed by signal-detection methods (17). For ease of exposition, we report the results in terms of percentage correct. Performance indices were estimated separately per subject and condition and tested for significance via Pearson's χ² calculated from the corresponding prime × response cross table, which is equivalent to tests of the hypothesis d′ = 0. Global tests are based on the χ² statistics summed across subjects and conditions (18).

Choice RTs were summarized by trimmed means on correct trials, determined per subject and condition. RT difference scores were analyzed by repeated-measures ANOVAs. Error bars in graphs are based on the ANOVA interaction error term (19) appropriate for the comparison given in the figure legends.

Results.

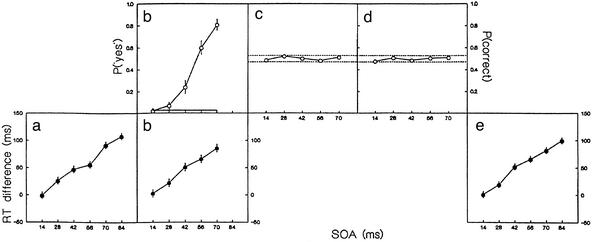
Fig. 2 displays measures of visibility (b Upper, c, and d) and RT effects (a, b Lower, and e) of primes as a function of SOA. Obviously, metacontrast masking precluded recognition of primes (Fig. 2 c and d) but not their detection (Fig. 2b). In the first session, none of the subjects spontaneously reported having seen the prime stimuli; two subjects indicated perception of flicker. In task b, detection probability increased from 0.023 at SOA = 14 ms to 0.810 at SOA = 70 ms, compared with an overall false-alarm rate of 0.026 on blank trials. These values correspond to detection d′s of -0.05 and 2.82, respectively. However, at none of the SOAs from 14 to 70 ms could subjects correctly report prime orientation, neither when recognition was performed separately (task d) nor jointly with choice reaction (task c): recognition performance remained at chance across >3,000 trials with error feedback (task c: χ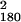 = 186.63, P = 0.352; task d: χ 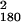= 200.61, P = 0.139). We analyzed recognition performance in greater detail, by sorting trials according to SOA, mask (left, right, or neutral), and whether mask shape varied or was constant within a block. Because mask orientation may bias recognition reports, sorting trials according to prime-mask congruency risks confounding sensitivity with bias. We therefore computed recognition d′ for each type of trial separately, and combined by averaging. When masked by a right or left mask, recognition performance yielded d′ = −0.003 in varied conditions (χ 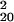= 21.52, P = 0.367) and d′ = 0.003 in blocked conditions (χ 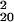= 19.10, P = 0.515). Even with neutral masks, performance was not reliably better than chance, although there were minimal improvements (varied: d′ = 0.078, χ 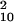= 15.17, P = 0.126; blocked: d′ = 0.111, χ 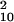= 14.17, P = 0.165).

Figure 2.

Masking and priming as a function of SOA in experiment 1. The sequence corresponds to the order in which the tasks were performed. a–e correspond to the letters assigned to the different tasks. (b–d) Detection and recognition of masked primes. (b) Hit rate (with symbols) and false alarm rate (solid line) in prime detection. (c and d) Probability of correct prime recognition. Dotted lines indicate region where performance is not significantly different from chance. (a, b, and e) Effect of prime-mask congruency on choice RT. (a) Initial session. (b) Middle session. (e) Final session. Error bars are based on the SE of the difference between two means; nonoverlapping error bars indicate that the corresponding means differ with α = 0.05. A breakdown of the choice RTs and error rates is provided in Tables 1 and 2, which are published as supporting information on the PNAS web site.

Although perfectly masked, primes produced huge and stable effects on the speed of choice responses to the mask. Congruent primes sped up and incongruent primes slowed down responses to the orientation of the mask. These effects strongly depended on prime-mask SOA (Figs. 1 and 2). The empirical priming function (the net effect RT_incong−RT_cong at a given SOA) was invariant across the different phases of the experiment: in task a, before subjects knew about the occurrence of the primes; in task b, where the combined choice RT and detection task required subjects to focus attention on both mask and prime; and in task e, after five sessions of prime recognition practice. Neither intercept nor slope (mean 1.54) of the priming function varied across sessions (F_2,10 = 0.007, P = 0.993).

Experiment 1 demonstrates a clear dissociation between masking and priming and provides compelling evidence for subliminal perception of masked prime stimuli. Note that prime stimuli were not subliminal in the sense that their presence or absence could not be detected, but the critical prime feature remained perfectly invisible. This is evident from the flat masking function at chance level, with zero d′ on recognition trials comparable to the choice RT task (left or right mask within mixed blocks). At the same time, the critical prime feature must have been processed, even though it did not reach conscious awareness. Thus, motor action cannot have been based on the targets' conscious representation exclusively.

Experiment 2

Experiment 1 showed robust priming effects within an SOA range where recognition performance was at chance. Could these findings be due to different sensitivity ranges of the direct and indirect measures, or do they truly reflect separate mechanisms for conscious perception and motor action? To answer these questions, we studied the time course of priming when perceptual masking allows better-than-chance recognition performance. We created stimulus conditions in which recognition accuracy either increased or actually decreased with SOA, within the same time range. Increasing and u-shaped time courses are known as “type A” and “type B” masking functions, respectively (11). If the priming time course were the same under type A and type B masking, this could not be accounted for by assuming that our direct and indirect measure tap at the same underlying information but differ in sensitivity (for a formal analysis, see Supporting Text I, which is published as supporting information on the PNAS web site, www.pnas.org). We thus systematically varied prime and mask durations, in addition to SOA. This manipulation made primes more visible and allowed us to assess whether the dissociation of masking and priming also holds for supraliminal primes.

Method.

Subjects.

Six students from Braunschweig University, age 21–29 years, were tested in seven 1-h sessions each. None had participated in experiment 1.

Design.

Stimuli and procedure were identical to those of experiment 1, except as described below. Choice reaction and prime recognition (corresponding to tasks a and d above) were tested separately, administered in the order a-d-a per session, each of which consisted of 504 choice reaction and 252 recognition trials. In recognition, only left and right masks were used, occurring equally often within blocks. Prime and mask duration varied randomly, with values of 14 or 42 ms each. The prime–mask interstimulus interval (ISI) varied between 0 and 70 ms in 14-ms steps. Thus SOA varied between 14 and 84 ms for 14-ms primes and between 42 and 112 ms for 42-ms primes.

Statistical methods.

Recognition performance was analyzed by repeated-measures ANOVAs of the arc-sine transformed frequencies of correct responses; signal-detection analyses (not reported) gave essentially the same results. Data reported are from sessions three to seven.

Results and Discussion.

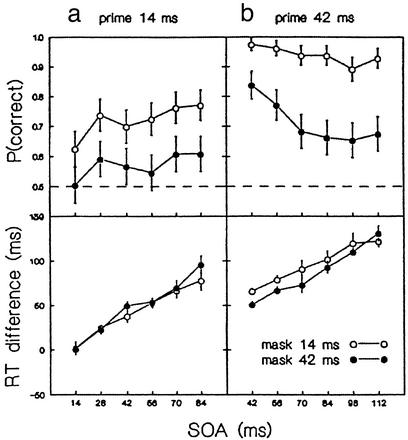
As expected, reducing mask and increasing prime duration vastly improved recognition performance. Varying mask duration produced almost additive effects, with short masks giving rise to less perceptual masking than long ones (mask: F_1,5 = 96.35, P < 0.0005; prime × mask: F_1,5 = .941, P = 0.377; mask × ISI: F_5,25 = 2.67, P = 0.046). Varying prime duration, in contrast, produced qualitative changes in masking dynamics (Fig. 3 Upper). Whereas short primes were recognized better the later the mask, recognition of long primes was best at shortest SOAs (prime: F_1,5 = 33.91, P = 0.002; prime × ISI: F_5,25 = 7.92, P < 0.0005). This shows that we were successful in producing perceptual masking with type A and type B time courses.

Figure 3.

Masking and priming as a function of SOA, prime duration, and mask duration in experiment 2. Error bars indicate ±SE around means. (Upper) Probability of correct prime recognition. (Lower) Effect of prime-mask congruency on choice RT. A breakdown of the choice RTs and error rates is provided in Tables 1 and 2. See also Supporting Text II.

This qualitative change in the masking function was in stark contrast to the priming effects on response time (Fig. 3 Lower). Again, congruent primes led to faster responding to the mask than incongruent primes, and the effect increased with SOA. Rather than resembling the masking function, however, the shape of the priming functions was similar to that observed in experiment 1 and remained invariant across changes in prime and mask duration. Although primes followed by long masks where clearly less visible than when followed by short masks, they produced equal effects on RT (mask: F_1,5 = 0.30, P = 0.606). Even more strikingly, the priming time course was almost identical for type A and type B masking (prime: F_1,5 = 0.67, P = 0.450, prime × ISI: F_5,25 = 0.73, P = 0.543). For 42-ms primes and masks, there was a remarkable double dissociation within the SOA range from 42 to 98 ms: the amount of priming increased, but recognition accuracy deteriorated with SOA. These findings suggest that the attributes of the masked primes that are relevant for the priming effect were fully processed, whether they reached visual awareness or not.

This conclusion is supported by an analysis of the choice error rates in both experiments. On congruent trials, the average error rate was <3% and did not systematically vary with SOA. On incongruent trials, however, the error rate increased dramatically with SOA for all subjects; Fig. 4c Upper Left shows this increase for subjects with many or few errors overall in experiment 2. This pattern rules out interpretations of priming due to fast guessing, triggered by the mere detection of the prime (20), and is at odds with the hypothesis that primes remain unprocessed themselves but exert their effects by facilitating or inhibiting the processing of the mask (6, 21). Instead, primes seem to fully activate the corresponding response, leading to incorrect responses on incongruent trials unless countermanded (which is possible at short SOAs only). This interpretation agrees with recent neurophysiological evidence for prime-related activation in the motor cortex (7, 22).

Figure 4.

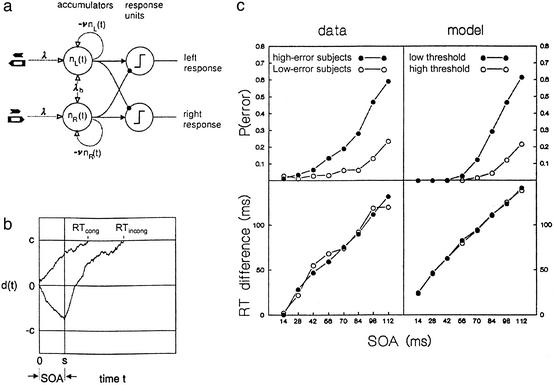
(a) Accumulator model. Primes and masks feed orientation-specific accumulators with rate λ each; accumulator states decay exponentially with rate ν. A response is initiated when the accumulator difference d(t) crosses the threshold c or –c. (b) Sample time courses of d(t) when a prime is followed by a congruent or incongruent mask with SOA = s. Responses on incongruent trials are delayed by s ms on average, as compared with congruent trials. (c) Observed and predicted error rates and priming effects. (Upper) Error rate on incongruent trials as a function of SOA, for high- and low-error subjects (Left), and as predicted for low and high thresholds (Right). (Lower) Identical priming functions predicted (Right) and observed for high- and low-error subjects (Left). Parameters used in Monte Carlo simulation: λ_b = 0.005, λ = 1.0, ν = 0.02, c_low = 45.0, c_high = 55.0, n = 5,000 replications.

An Accumulator Model of Priming

How can one account for the differently shaped time courses in masking and priming? The temporal dynamics of metacontrast masking seems well understood with regard to its perceptual aspects (refs. 23 and 24, but see ref. 25). However, priming phenomena and their dissociation from masking are not covered by current masking theories, and we doubt that a single-process theory can account for the dissociation (see Supporting Text II). Rather, we focus on the temporal dynamics of early priming, i.e., within the short time range covered in our experiments. To set constraints on such a model, we analyzed the RT data from experiment 2 more closely. They are fit surprisingly well by the linear function RT_incong−RT_cong = SOA + b, with slope = 1 and intercept b = 0, except for the 42-ms primes. Within the overlapping SOA range from 42 to 84 ms, the slopes of the four empirical priming functions did not differ from 1 (mean = 0.96; F_1,5 = 0.12, P = 0.74). As in experiment 1, the slopes were slightly steeper at short SOAs.

The unit slope finding is puzzling, because in most models the predicted slope depends on the particular parameter values. We propose a simple model that predicts the slope nonparametrically. It is similar to the neural accumulator model of Hanes and Schall (26) but includes saturation in the stochastic accumulation process. Our model assumes separate accumulators collecting sensory evidence for stimuli mapped to left or right responses (Fig. 4a). Inputs to the accumulators are spike trains, modeled as inhomogeneous Poisson processes. Spikes increment the accumulator counts; their momentary arrival rates depend on whether the stimulus to which an accumulator is tuned currently resides in a sensory buffer. For simplicity, we assume that primes and masks are equally effective in driving the accumulators. A response is initiated as soon as the accumulated neural evidence for one vs. the opposite response exceeds some critical value, c. Saturation is modeled as random decay of the accumulated spikes. Sample realizations are shown in Fig. 4b.

For each accumulator, the input rate equals λ + λ_b when there is sensory input from the stimulus to which the accumulator is tuned and λ_b otherwise. Accumulated effects decay with instantaneous rate nν, where ν is the decay parameter and n the current number of accumulated nondecayed effects. Primes remain effective until the mask appears.

The model predicts response priming because primes bias the accumulators, driving their difference toward the target threshold on congruent trials and away from it on incongruent trials (for derivations, see Supporting Text II). Approximating mean reaction time by the time for the mean difference to reach threshold, the predictions for congruent and incongruent trials equal

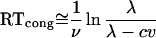and

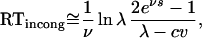respectively. Therefore, the net priming effect at prime-mask SOA = s equals

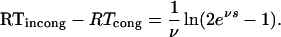This function is almost linear in SOA, with shape depending on the decay parameter but not on the accumulation rates or the response threshold. Its slope equals 1 ≤ 1/(1 − e^−νs/2) ≤ 2, SOA = s ≥ 0, tending to 1 for prime-mask SOA sufficiently large.

Because there is no guarantee that results based on the mean process approximation are close to those for the stochastic process (27), we checked the slope prediction by Monte Carlo simulation. Fig. 4c Lower Right shows typical results. As can be seen, the simulated priming functions are approximately linear, with slope approaching 1. Confirming the approximation, they do not depend on the response threshold. In contrast, the predicted error rate on incongruent trials increases more steeply with SOA for lower than for higher response thresholds (Fig. 4c Upper Right).

Evaluation of the Model.

The model gives an excellent account of the shape and slope of the empirical priming functions in both experiments. The unit-slope prediction depends crucially on the assumption of negatively accelerated identical information accrual from prime and mask. Without saturation, accumulation models predict priming functions with slope close to 2, unless rates differ for prime and mask.‖ Several more advanced but less tractable models have been proposed recently that include saturation or leakage (e.g., refs. 29 and 30) and may also be able to account for our data.

The priming function predicted by our model is insensitive to changes in rate and threshold parameters, which explains the surprising stability of the empirical priming function across conditions. In contrast, the model predicts that error rate (like absolute RTs) does depend on these parameters. This predicted dissociation was found when we compared priming effects of subjects with many and with few overall errors in experiment 2. If error rate differences between subjects reflect differences in response threshold, identical priming functions are predicted, and in fact, no difference was found in the empirical priming function for high-error and low-error subjects (Fig. 4c Lower Left).

Note that our model assumes a single-response decision based on the accumulator difference, rather than separate decisions for each accumulator. Additional analytical and Monte Carlo studies have revealed that the separate-decision version, while not equivalent to the difference model presented here, leads to very similar predictions.** The issue of combined vs. separate decisions becomes crucial, however, when the model is extended to more than two response alternatives (31).

General Discussion

Our experiments have revealed two types of dissociation between masking and priming. Subliminal priming refers to the finding that the priming function increases with SOA, despite perfect masking. This is compelling evidence for behavioral effects of stimulus properties that do not access awareness and suggests that metacontrast masking abolishes conscious perception of some of the prime's features, but not those features' motor effects. Invariant priming with and without awareness concerns the finding that the priming function is shape invariant in the face of qualitative changes in masking dynamics. Such a dissociation cannot be accounted for by assuming that masking and priming reflect the same underlying process (see Supporting Text II). Invariant priming was found for complete masking, type A masking, and type B masking, and implies visuomotor mechanisms for which conscious perception is not a prerequisite. One possible implementation of such a mechanism is the neural accumulator model proposed here.

At first sight, invariant priming seems at odds with qualitative differences in the effects of unconscious and conscious prime stimuli reported recently (32–34). We believe that those findings reflect conscious control of action, which arises relatively late in the processing chain. In contrast, invariance of priming with and without awareness is a characteristic of early processing stages and is typically found in experiments with prime-target-SOAs of <100 ms (unpublished data).

The reported masking and priming dissociations are consistent with the notion of separate action and perception systems (3), assuming that within the perception system, processing is interrupted and stimuli remain invisible if new input arrives before boundary contours have been computed and filled in (23, 35). This view is backed by neurophysiological and psychophysical evidence (36–39). In single-cell recordings, Macknik and Livingstone (40) have observed an after-discharge of cells in V1 some 100 ms after prime offset, which seems crucial for conscious perception because it is suppressed when a mask follows. The action system, in contrast, seems to have access to shape information of unseen stimuli, possibly from their unfilled contours, and to integrate rather than overwrite evidence from prime and mask. Information integration across prime and mask is the crucial assumption underlying the accumulator model. Recent research in our lab has revealed its signature, the unit-slope priming function, for other types of stimuli and responses as well, e.g., color (41) and semantic stimuli (unpublished data), and saccadic eye movements (31), pointing (42), and vocal responses. These findings do not agree with central notions of Milner and Goodale's theory (3), such as the role of color processing in the action system and the importance of hard-wired connections to effectors. Instead, these data suggest the workings of a general-purpose decision module, probably located within the prefrontal cortex, which is programmable to link arbitrary sensory output to action.

The findings reported here show that perceptual measures based on conscious reports do not suffice to determine whether particular information is available to the visual system at large. Instead, motor and perceptual effects can be dissociated, indicating that relevant stimulus attributes may be fully processed up to the level of response control but remain unavailable for conscious report. We have shown here that this holds within the first 100 ms of visual processing. Extending our approach of dissociating perception and action by their time courses to the range 100–500 ms (unpublished data) has revealed that additional mechanisms soon come into play, which drastically alter the simple picture of early priming seen here. It is important to stress that the present findings are specific to the particular time range and have to be carefully distinguished from priming mechanisms within different time ranges, which seem to follow different laws (43–45). We believe that further research will uncover a host of priming mechanisms, which overlap in time and depend on conscious awareness to different degrees.

Abbreviations

SOA

stimulus-onset asynchrony

RT

response time

ISI

interstimulus interval