Abstract
The plasma membrane of various mammalian cell types is heterogeneous in structure and may contain microdomains, which can impose constraints on the lateral diffusion of its constituents. Fluorescence correlation spectroscopy (FCS) can be used to investigate the dynamic properties of the plasma membrane of living cells. Very recently, Wawrezinieck et al. (Wawrezinieck, L., H. Rigneault, D. Marguet, and P. F. Lenne. 2005. Biophys. J. 89:4029-4042) described a method to probe the nature of the lateral microheterogeneities of the membrane by varying the beam size in the FCS instrument. The dependence of the width of the autocorrelation function at half-maximum, i.e., the diffusion time, on the transverse area of the confocal volume gives information on the nature of the imposed confinement. We describe an alternative approach that yields essentially the same information, and can readily be applied on commercial FCS instruments by measuring the diffusion time and the particle number at various relative positions of the cell membrane with respect to the waist of the laser beam, i.e., by performing a Z-scan.
Due to a variable degree of lipid miscibility (1), cellular membranes contain a variety of molecular complexes and domains, characterized by different composition and spatial arrangement of the lipids constituting the membrane. One class of membrane inhomogeneities are the so-called lipid rafts. These liquid-ordered microdomains, built mainly of cholesterol and saturated lipids, attract a lot of interest as they are thought to provide dynamic platforms that are involved in a variety of processes, such as signal transduction and protein and lipid sorting (2).
Most of the experimental evidence concerning the existence of rafts in cellular membranes comes from biochemical studies, which show that some membrane constituents are resistant to solubilization by nonionic detergents at low temperature (3). However, as application of a detergent can alter the membrane phase behavior (4), alternative in situ methods are required.
Another type of membrane inhomogeneity is the confined diffusion of membrane constituents within membrane compartments made up by the membrane-associated actin cytoskeleton (fences) and by rows of transmembrane proteins anchored to it (pickets) (1).
Several microfluorimetric methods (5) have been applied to study the dynamics of membrane constituents within the context of the lateral microheterogeneity of the cellular membrane. In fluorescence correlation spectroscopy (FCS) small fluctuations in the fluorescence signal from a femtoliter observation volume are measured over a short period of time. These fluctuations arise from fluorescently labeled molecules diffusing in and out of the observation volume, which is spatially defined by the laser focus. The corresponding autocorrelation function (ACF) contains information about the average number of molecules in the observation volume and their characteristic diffusion time as measured by the full width at half-maximum of the ACF (6). It was recently demonstrated that FCS has the potential to be a valuable tool in the study of lipid raft associations, both in model membranes exhibiting domains and in cell membranes (7,8).
For hindered or confined diffusion and for the case where the area of confinement is several times smaller than the beam area, the relation between the diffusion time τD and the beam area is given by (8)
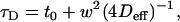 |
(1) |
where w is the radius of the beam at the plane of diffusion, Deff the so-called effective diffusion coefficient, and t0 a constant. For free diffusion, t0 is equal to zero. A nonzero value for t0 is indicative of hindered diffusion and is proportional to the confinement time within the microdomains. If t0 > 0, the confinement is due to rafts; if t0 < 0, the confinement is due to a meshwork (8).
The consequence of these observations is that single-waist FCS measurements are not sufficient in the case of hindered diffusion and measurements at different waist sizes are necessary. This requires either a beam expander or underfilling of the objective, which may be a technical problem for most commercial FCS instruments. In this letter, we introduce an alternative based on the Z-scan method. This approach was used for precise determination of the diffusion coefficient in supported phospholipid bilayers (SPBs) (9). The method is based on acquiring consecutive sets of FCS measurements along the z axis of the instrument.
For a Gaussian beam, the radius w can be expressed as (10)
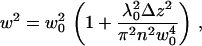 |
(2) |
where w0 is the radius of the beam in the waist, λ0 is the wavelength of the excitation light in vacuum, n is the refractive index of the medium, and Δz is the distance between the sample position and the position of the minimum laser-beam diameter. The average number of particles N in the illuminated membrane surface within the confocal volume at each value of Δz is given by
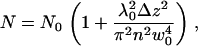 |
(3) |
where 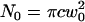 and c is the average concentration of diffusing fluorescent molecules in a plane perpendicular to the beam. For free diffusion with diffusion coefficient D, the z-dependence of the diffusion time is given by
and c is the average concentration of diffusing fluorescent molecules in a plane perpendicular to the beam. For free diffusion with diffusion coefficient D, the z-dependence of the diffusion time is given by
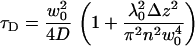 |
(4) |
From the known dependencies of τD and N on the z-position of the plane, the lateral diffusion coefficient and the surface concentration can be obtained without the need for an extrinsic calibration. The method generally allows for precise positioning of the membrane in the waist of the beam and increases the accuracy of the measurements.
For the case of confined diffusion, the relation between τD and N is given by
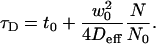 |
(5) |
Equation 5 is formally equivalent to Eq. 1 and implies a parabolic dependence of the diffusion time on Δz.
We explored the Z-scan method to evaluate the diffusion of the membrane marker 1,1′-dioctadecyl-3,3,3′,3′-tetramethylindodicarbocyanine perchlorate (DiD) (Molecular Probes, Eugene, OR) in SPBs (11) and in the plasma membrane of OLN-93 cells (oligodendroglioma derived from primary rat brain glial culture (12)).
SPBs were prepared from small unilamellar vesicles (SUVs) resulting from sonication of multilamellar vesicles obtained from resuspending a dried mixture of DOPC and DOPS (DOPC/DOPS = 4:1). Labeled SUVs were prepared in the presence of DiD (lipid/dye = 10,000:1). Mica slides were fixed to a microscrew and positioned in a cuvette. Labeled and nonlabeled SUVs were mixed (1:9), and 50 μL of the mixture was added to the cuvette. After at least 30 min, the SPB was formed and remaining SUVs were washed away.
OLN-93 cells were grown in eight-well glass LabTek chambers (Nalge Nunc, Rochester, NY) in growth medium (GM). Cells were labeled with DiD (5 μM DiD in GM for 15 min at 37°C). FCS measurements were performed in HEPES buffered phenol red-free medium supplemented with 10% serum. The measurements were performed at the membrane facing the supporting glass. All data were corrected for the constant background of 1 kHz.
FCS and confocal imaging were carried out on a Zeiss Confocor 2 microscope (Carl Zeiss Microscopy, Jena, Germany) with a 40×, NA 1.2 water immersion objective. The pinhole was set at 90 μm. Samples were excited with a 633 nm He-Ne laser at 0.1% of the maximum laser power to prevent photobleaching as much as possible. In addition to the triplet formation of DiD the cis-trans transition was also taken into account. The ACF G(τ) is given by
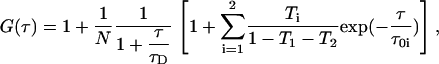 |
(6) |
where τ01 and τ02 are the inverse of the triplet rate constant and the cis-trans transition rate constant, respectively; and T1 and T2 are the corresponding amplitude fractions.
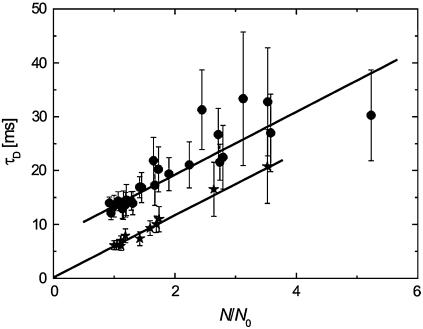
The results obtained on SPBs (Fig. 1 and Table 1) clearly indicate that DiD in the SPBs exhibits free diffusion.
FIGURE 1 .
Results obtained for DiD in DOPC:DOPS SPBs on mica (★) and in OLN-93 (•). Error bars represent standard errors.
TABLE 1.
Effective diffusion coefficients of DiD in SPBs and OLN-93 cells obtained from a Z-scan at room temperature
| t0 (ms) | Deff (μm2 s−1) | |
|---|---|---|
| SPB | 0.2 ± 1.6 | 5 ± 1 |
| SPB | 0 (fixed) | 4.4 ± 0.3 |
| OLN-93 | 8 ± 1 | 4.5 ± 0.8 |
Obtained from weighted linear least-squares fitting using Eq 5; uncertainties are reported as standard error.
The waist of the laser was estimated by using the parabolic fit (w0 = 0.323 ± 0.008 μm) and by applying an extrinsic calibration using Cy5 (Amersham Biosciences, Uppsala, Sweden) in water and assuming a diffusion coefficient of 316 μm2/s (w0 = 0.335 ± 0.010 μm). The values of the diffusion coefficient of DiD correspond with those reported in the literature (13).
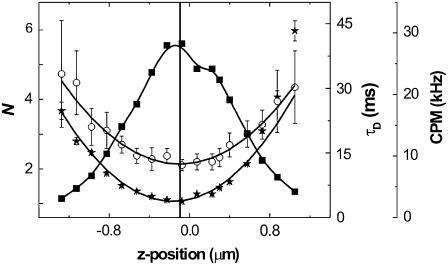
The results obtained for OLN-93 are shown in Figs. 1 and 2 and in Table 1. It has to be emphasized that good fits were obtained by using Eq. 6 for each of the ACF collected at the various values of Δz. The value for t0 is significantly greater than zero, suggesting hindered diffusion by rafts, according to the model suggested by Wawrezinieck et al. (8). Similar results were obtained in 15 independent cell measurements.
FIGURE 2 .
Results obtained for DiD in OLN-93. CPM is counts per second per molecule. CPM, ▪; τD, ○; and N, ★. Error bars represent standard errors.
In conclusion, it can be stated that single-waist FCS measurements do not allow for a complete description of the lateral diffusion in the cellular membrane. Plotting the apparent diffusion times versus the relative particle number, which is a measure of the illuminated area, clearly indicates hindered diffusion. The proposed Z-scan yields the same type of information as that obtainable by changing the waist of the laser beam (8) and can be applied on commercial FCS instruments. The additional benefits are that the Z-scan approach implicitly considers optimal position of the membrane in the focus volume, leads to improved precision of the recovered parameters, and unreliable measurements are easily identified.
Acknowledgments
We thank Prof. Dr. C. Richter-Landsberg, Molecular Neurobiology Department, Oldenburg University, Germany, for the OLN-93 oligodendroglial cells.
This work has been supported by the Research Council of the UHasselt and tUL, the K.U. Leuven (grant No. GOA/2006/02), a bilateral project (grant No. BIL03/08) between Flanders and the Czech Republic, the Grant Agency of the Czech Republic (A.B. and M.H. via grant No. 203/05/2308), and the Ministry of Education, Youth and Sports of the Czech Republic (J.H. and V.F. via grant No. LC06063).
J. Humpolíčková and E. Gielen contributed equally to this work.
References
- 1.Kusumi, A., I. Koyama-Honda, and K. Suzuki. 2004. Molecular dynamics and interactions for creation of stimulation-induced stabilized rafts from small unstable steady-state rafts. Traffic. 5:213–230. [DOI] [PubMed] [Google Scholar]
- 2.Simons, K., and E. Ikonen. 1997. Functional rafts in cell membranes. Nature. 387:569–572. [DOI] [PubMed] [Google Scholar]
- 3.Brown, D. A., and J. K. Rose. 1992. Sorting of GPI-anchored proteins to glycolipid-enriched membrane subdomains during transport to the apical cell surface. Cell. 68:533–544. [DOI] [PubMed] [Google Scholar]
- 4.Heerklotz, H. 2002. Triton promotes domain formation in lipid raft mixtures. Biophys. J. 83:2693–2701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Lommerse, P. H., H. P. Spaink, and T. Schmidt. 2004. In vivo plasma membrane organization: results of biophysical approaches. Biochim. Biophys. Acta. 1664:119–131. [DOI] [PubMed] [Google Scholar]
- 6.Haustein, E., and P. Schwille. 2004. Single-molecule spectroscopic methods. Curr. Opin. Struct. Biol. 14:531–540. [DOI] [PubMed] [Google Scholar]
- 7.Bacia, K., D. Scherfeld, N. Kahya, and P. Schwille. 2004. Fluorescence correlation spectroscopy relates rafts in model and native membranes. Biophys. J. 87:1034–1043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Wawrezinieck, L., H. Rigneault, D. Marguet, and P. F. Lenne. 2005. Fluorescence correlation spectroscopy diffusion laws to probe the submicron cell membrane organization. Biophys. J. 89:4029–4042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Bendá, A., M. Benes, V. Marecek, A. Lhotsky, W. T. Hermens, and M. Hof. 2003. How to determine diffusion coefficients in planar phospholipid systems by confocal fluorescence correlation spectroscopy? Langmuir. 19:4120–4126. [Google Scholar]
- 10.Sorscher, M. S., and M. P. Klein. 1980. Profile of a focused collimated laser beam near the focal minimum characterized by fluorescence correlation spectroscopy. Rev. Sci. Instrum. 51:98–102. [Google Scholar]
- 11.Spink, C. H., M. D. Yeager, and G. W. Feigenson. 1990. Partitioning behavior of indocarbocyanine probes between coexisting gel and fluid phases in model membranes. Biochim. Biophys. Acta. 1023:25–33. [DOI] [PubMed] [Google Scholar]
- 12.Richter-Landsberg, C., and M. Heinrich. 1996. OLN-93: a new permanent oligodendroglia cell line derived from primary rat brain glial cultures. J. Neurosci. Res. 45:161–173. [DOI] [PubMed] [Google Scholar]
- 13.Kahya, N., D. Scherfeld, K. Bacia, B. Poolman, and P. Schwille. 2003. Probing lipid mobility of raft-exhibiting model membranes by fluorescence correlation spectroscopy. J. Biol. Chem. 278:28109–28115. [DOI] [PubMed] [Google Scholar]