Abstract
A change in cellulose lattice spacing can be detected during the release of wood maturation stress by synchrotron x-ray diffraction experiment. The lattice strain was found to be the same order of magnitude as the macroscopic strain. The fiber repeat distance, 1.033 nm evaluated for tension wood after the release of maturation stress was equal to the conventional wood values, whereas the value before stress release was larger, corresponding to a fiber repeat of 1.035 nm, nearly equal to that of cotton and ramie. Interestingly, the fiber repeat varied from 1.033 nm for wood to 1.040 nm for algal cellulose, with an increasing order of lateral size of cellulose microfibrils so far reported. These lines of experiments demonstrate that, before the stress release, the cellulose was in a state of tension, which is, to our knowledge, the first experimental evidence supporting the assumption that tension is induced in cellulose microfibrils.
INTRODUCTION
Wood in living trees undergoes large mechanical stresses, called growth stresses. Growth stresses result from the superposition of two kinds of stress (1): support stress, that is, an elastic response to the increasing load of wood and shoots supported by the tree, and maturation stress, which appears spontaneously inside wood during its formation. Maturation stress allows the tree to adapt to various mechanical constraints (1–3). Tensile longitudinal stress in the periphery of the trunk optimizes the resistance of wood against bending forces such as wind. Heterogeneous distribution of this stress around the tree circumference generates a bending moment, which allows the change in orientation of the tree trunk and branches, necessary for the tree to stay upright and maintain its branches at an optimal angle.
The circumferential heterogeneity of maturation stress is achieved through the production of a special kind of wood on one side, called reaction wood. In hardwood, this wood is formed on the upper side of the leaning stem and associated to a large longitudinal tensile stress, and thus called tension wood (4). In many hardwood species (2,5,6), tension wood is associated to the formation of a peculiar layer of the fiber wall, the gelatinous layer (7–10) where the cellulose microfibrils are aligned nearly parallel to the fiber axis (11–13).
At the tree level, the apparition of a tensile stress in the newly formed wood layers is related to the conjunction of two facts: during its formation, the wood have a spontaneous tendency to shrink longitudinally; but this tendency is impeded because the new wood is strongly glued to the internal older wood, so that a tensile longitudinal stress results. The magnitude of the maturation stress can be estimated at the surface of living trees, by mechanically dissociating a portion of wood from the rest of the tree, and recording the generated strain (14,15). The order of magnitude of the measured longitudinal strains is ∼−300 microstrains (μm/m) in normal wood and can be up to −3000 microstrains in tension wood.
At a microscopic level, the mechanism responsible for the tendency of wood fibers to shrink (i.e., the mechanism of maturation stress generation) is still a matter of discussion. It has been proposed that it could be due to the swelling of the wood matrix substance during lignification (16), the angle of cellulose microfibrils controlling the anisotropy of the resulting stress. However, this mechanism is unable to explain the large tensile stress found in tension wood, and especially in G-layer tension wood. As an alternative assumption, the hypothesis of a shrinkage of cellulose microfibrils was proposed (17,18). Results obtained using micromechanical models showed that, to account for the observed relation between microfibril angle and released maturation strains, a combination of both assumption was necessary (19–21). However, the proposed mechanisms remained hypothetical, and no evidence has been yet provided of such behavior at the macromolecular level. In particular, how a tensile stress could be induced inside the cellulose crystal is still rather enigmatic.
The crystalline cellulose is an aggregate of cellulose molecules and exists in a form of crystalline microfibril. The molecules are synthesized unidirectionally in a way that the reducing end points away from the loci of the synthesis (22), so-called cellulose synthesizing terminal complex in the plasma membrane. These nascent parallel cellulose chains are known to be crystallized into cellulose Iα and Iβ depending on the plant sources (23,24). Despite the allomorphism of crystals, the length of the fiber repeat estimated from the meridional reflection in x-ray or electron diffraction spot (004) for monoclinic indexing and (1̄1̄4) for triclinic indexing (24) has been thought to be common in all native cellulose. The fiber repeat (c axis distance) is a measure of two successive 1,4-linked β-glucose residues and calculated from the 4 times of 004 d-spacing. If sufficient precision is achieved, the change in fiber repeat during the tensile test can be measured and thus crystal strain can be obtained (25). The relative change in lattice spacing is referred to as lattice strain, and is a measure of the strain at the ultra-structural level, inside the cellulose crystal. It can be compared to the macroscopic strain, measured at the surface of wood (26–29).
The study presented here focuses on the behavior of cellulose microfibrils in relation to maturation stress. Poplar tension wood was chosen for study partly because its highly oriented microfibrils are suitable for x-ray pattern quality (5) and the crystalline features are well investigated (13,30–33), and partly because the presumed large magnitude of the tensile maturation stress allows strains easier to observe. The primary purpose of this study is to show measurements of lattice spacing before and after the release of maturation stress and compare the lattice strain to the related surface strain. Lattice spacing measurements were performed using a synchrotron facility. Similar observations were also performed for the strains associated to the drying of poplar wood, using a standard laboratory x-ray apparatus. This aims at comparing the shrinking process occurring during maturation stress release to that occurring during drying. The absolute value of lattice spacing in these various conditions is compared to values of lattice spacing obtained from standard cellulose samples such as ramie, cotton, and algae, to discuss the mechanical state of cellulose in tension wood and its possible implication in the generation of maturation stress.
MATERIALS AND METHODS
Plant material and sample preparation
Experiments were performed on poplar wood (Populus euramericana). A lateral branch, ∼10 cm in diameter, was chosen for synchrotron experiments. Before taking off the branch, a strain gauge was glued on the wood surface on its upper side, to control continuously the possible release of maturation stress due to manipulation and sample preparation. The branch was then sawn, and two 40-cm long logs were taken for the synchrotron experiment. During this time, the branch was prevented from dehydration, by wrapping it into a polyethylene film and humidifying it with wet towels.
For laboratory experiments on wood samples, small samples were collected on the upper side of a tilted trunk, after measuring the released maturation strains. High tensile stress was detected and anatomical observations confirmed the presence of gelatinous fibers. The wood was kept wet during transportation and sample preparation. Specimens were machined 1 × 5 × 30 mm respectively along the radial, tangential and longitudinal directions.
Specimens of alga (Cladophora sp.) were collected in the sea at Chikura (Japan). The stem internodal cell, being both ends cut-opened (1–2 cm long) was collected and treated by boiling in 0.1 N NaOH for 3 h, followed by overnight immersion in 0.05 N HCl at room temperature. The treatment was repeated twice until the cell wall became transparent. Cellulose from ramie (Boehmeria sp.) was collected in campus of Uji (Kyoto University, Japan), and purified by bleaching in 0.3% NaClO2 at 70°C (pH 4.9), followed by overnight immersion in 5% KOH and washing in distilled water. It was repeated until the fiber became perfectly white. Cellulose from cotton (dewaxed laboratory cotton) was used without further treatment.
Synchrotron x-ray experiments
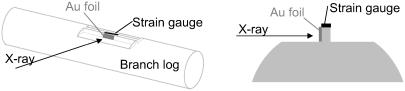
The branch logs were prepared for the synchrotron experiment. Wood was removed on a depth of 5 mm besides the strains gauge, to leave a 1-mm thin, 5-mm high, 50-mm long radial-longitudinal plate (Fig. 1). Gold foil was used as calibration reference. The Cladophora cell was also lapped with a gold foil and mounted with its longer axis horizontal as one of the two major microfibril orientation is roughly parallel to the long axis.
FIGURE 1.
Schematic diagrams of sample preparation for the synchrotron x-ray experiment. Three-dimensional view (left) and its cross-sectional view (right).
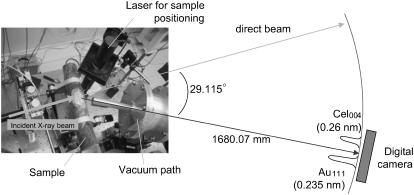
The synchrotron x-ray experiment was performed at the high flux beam line BL40XL beam line, SPring8, Harima, Japan, with the approval of the Japan Synchrotron Radiation Research Institute (JASRI, proposal No. 2003B0463-NL2a-np, 2004A0036-NL2a-np). The experiment was repeated twice but the experimental setup was slightly different. In the former beam time, the sample-to-camera distance was set around 320 mm so that the direct beam and the target (004) reflection from cellulose were recorded in the same frame. In the latter beam time, to gain maximum spatial resolution, the CCD camera was positioned in 1680 mm distance from the sample with an angle of 29.115° to the incident beam to record both (004) reflection from cellulose and (111) from gold foil for calibration as shown in Fig. 2. The vacuum path was placed between the sample and the camera to reduce the background due to the air scattering. The energy was 10 keV (wavelength = 0.124 nm) and typical exposure time was 0.5 s. The final resolution on the CCD camera was 0.0001° at 2.7 pixel.
FIGURE 2.
Experimental setup at BL40XU, SPring8, Harima, Japan. The log was tightly fixed being tilted ∼15° with respect to the incidence so that the (004) planes satisfy Bragg condition. The vacuum path of 1.5 m was inserted to suppress the background due to the air scattering.
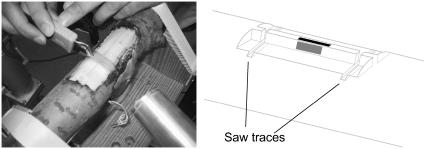
The wood log was positioned so that x-ray impacted half a millimeter below the wood surface where the strain gauge was pasted. After recording the x-ray diffraction pattern in this configuration, the sample was sawn manually at both sides of the strain gauge (Fig. 3) to release maturation stress. Macroscopic released maturation strain was measured from the strain gauge and a new x-ray diffraction pattern was then recorded in released configuration. The shape of the peaks obtained from this experiment did not allow it to fit properly to either a Gaussian or a parabolic shape, so that an alternative procedure was used to evaluate the shift in lattice spacing before and after maturation stress release. The location of the maximal value was recorded on the x-ray diffraction obtained before stress release. Then, the change in lattice spacing was obtained by a nonparametric fit method, in which the second series of data is shifted until the distance between the two data series is minimized.
FIGURE 3.
Photo showing the sawing to release the maturation stress (left) and a schematic of the saw traces after cutting (right). The sample has been fixed, always moistened, and the position was carefully monitored by a laser device until the second exposure was made.
Laboratory x-ray experiments
The specimens were mounted on a goniometer, and the θ–2θ scan was carried out in a referential transmission mode for values of 2θ ranging between 30° and 40°. Scanning was performed by a step-scan mode with a 0.01° step and 20 s exposure time. CuKα x-ray radiation was generated by RIGAKU Ultra18HF operated at 30kV, 300mA. NaF and gold foil were used as references. The d-spacing of the (004) crystal plane was evaluated the following way: a window was chosen around the visually located maximum intensity, and a parabolic function was fitted to the intensity profile in this window. The d-spacing value was taken as the maximum of the fitted function. These measurements were performed on the wet (water saturated) samples, and on the same sample after oven-drying.
RESULTS
Effect of sample preparation on the macroscopic strain
The effect of the sample preparation on the stress release was controlled. During sectioning the log, some strain occurs due to a spring-back effect related to the suppression of the weight of the end of the branch. This strain ranged between −100 and −200 μstrain, which is <10% of the total released strain. During sample preparation, wood was removed from both lateral sides of the strain gauge (cf. Fig. 1). As the removed wood was in a state of longitudinal tension, a redistribution of stress occurs inside the log. As a consequence, some additional tension appears in the left wood plate to balance the stress preexisting in the opposite side of the log.
Change in lattice spacing during maturation stress release
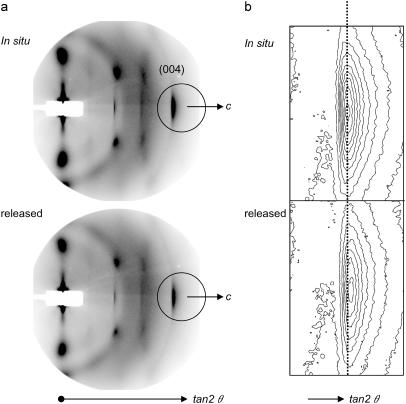
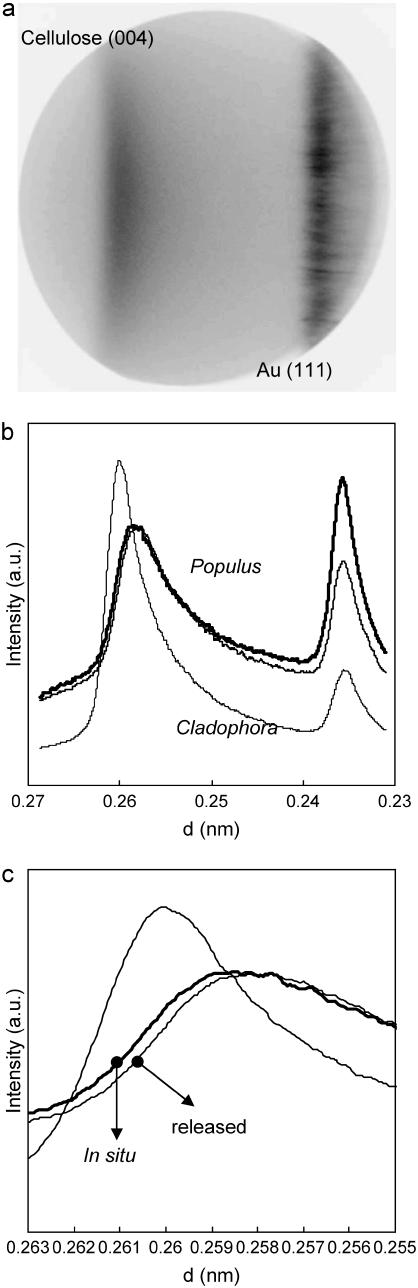
Typical diffraction patterns of P. euramericana before (in situ) and after the release of the maturation stress are shown in Fig. 4. The (004) meridional diffraction of cellulose crystallites appears on the right side of the diagram (Fig. 4 a). As mentioned earlier, the orientation of cellulose crystallites in tension wood are quite good and it can be monitored from the arcing of (004). In addition, the diagram indicates that the cellulose microfibrils are almost parallel to the longitudinal direction of a tree, and thus suited for our purpose. Two diffraction diagrams in situ and after the stress release were recorded and the position of (004) reflection was scrutinized. As shown in Fig. 4 b, a shift of 1 or 2 pixel was reproducibly observed in a contour map. However, the resolution of the imaging condition was not optimized to allow correlation between the lattice strain and the macroscopic strain.
FIGURE 4.
A typical diffraction patterns (a) obtained from P. euramericana tension wood in situ and after the stress release from the first cycle of synchrotron x-ray experiment (JASRI proposal No. 2003B0463-NL2a-np). The distance between sample and camera was ∼320 mm. As in enlarged contour plot (b) of the encircled area in a, the peak position of (004) diffraction shifted toward the higher angle (to the right), indicating that the fiber repeat distance is contracted upon the release of the maturation stress. The shift was, however, in the range of a few pixels so that the longer camera length is requisite to improve the resolution of the experiment. Yet no quantitative values were obtained during this experiment but the shift was constantly observed in the same direction. Fiber axis is horizontal.
To gain the maximum spatial resolution, the sample-camera length was readjusted to cover only (004) of cellulose and (111) of gold to calibrate. An example is presented in Fig. 5 a, where the pattern corresponding to the encircled area in Fig. 4 a is captured. More than 6 sets of two diagrams in situ and after stress release was obtained and scrutinized. All the diagrams were radially integrated to obtain diffraction profiles as in Fig. 5, b and c. The horizontal axis was converted to the lattice spacing in nanometer, which is reciprocal to the scattering angles. Almost all the specimens have the same trend that the shift occurs to yield shorter lattice spacing. As represented in Fig. 5, b and c, the (004) diffraction peak shifted, whereas the Au diffraction ring remained constant, showing that it is no experimental artifact. Therefore without ambiguity the cellulose crystallites in tension wood were found to contract during the release of the maturation stress. Estimated values of lattice spacing for tension wood samples before and after stress release are shown in Table 1. The macroscopic strain, recorded by the strain gauge, and the lattice strain, defined as the relative variation in lattice spacing, are also shown in Table 1.
FIGURE 5.
Second cycle of synchrotron x-ray experiment (JASRI proposal No. 2004A0036-NL2a-np). The distance between sample and camera was set ∼1.5 m to record only the encircled area in Fig. 5 a. A typical screen shot from P. euramericana tension wood is shown in a, showing (004) diffraction arc of cellulose and (111) diffraction ring of gold to calibrate. Radial integration profiles of the diffraction intensity were shown in b. Note that the calibration (111) of gold stays unchanged during the experiment. Enlargement at (004) diffraction peaks of cellulose samples is reproduced in c, where one can see clearly the shift toward the smaller lattice spacing (there is a reciprocal relationship between scattering angle in Fig. 5 and lattice distance) after the release of maturation stress. It is also interesting that the Cladophora shows much larger lattice spacing than wood cellulose, and the difference is much larger than the difference of P. euramericana wood in situ and after the stress release.
TABLE 1.
Results of the synchrotron x-ray experiment: change in lattice spacing and macroscopic strain during maturation stress release of P. euramericana tension wood
| Log No. 1 | Log No. 2 | |
|---|---|---|
| Lattice spacing (nm) | ||
| In situ (before release) | 0.25847 | 0.25896 |
| After stress release | 0.25818 | 0.25877 |
| Strain (μm/m) | ||
| Lattice strain | −1142 | −763 |
| Macroscopic strain | −1478 | −678 |
Another interesting feature is in comparison with other algal cellulose (Cladophora sp). Lattice spacing of algal cellulose was evaluated as 0.25992, and is clearly larger than tension wood cellulose lattice spacing.
Change in lattice spacing during tension wood drying
Diffraction profiles around the (004) reflection plane obtained in the laboratory x-ray experiment for ramie, cotton, and a tension wood sample in wet and dry state are shown in Fig. 6. Lattice spacing of ramie was evaluated as 0.25872 and that of cotton as 0.25873. That of water-saturated tension wood is lower, and slightly reduced after drying. The experiment was repeated for another tension wood sample, with qualitatively similar results. The estimated lattice spacings and the deduced lattice strains are shown in Table 2. The macroscopic strain could not be measured precisely on these samples, but for tension wood the order of magnitude of this shrinkage is between −8000 and −10,000 microstrains (34).
FIGURE 6.
Enlarged conventional x-ray diffractometry profiles at (004) cellulose diffraction from wet and dry P. euramericana tension wood together with ramie and cotton as references. The lattice contraction due to drying was very small and again the difference between wood and ramie/cotton cellulose was emphasized.
TABLE 2.
Results of the laboratory experiment: change in lattice spacing and macroscopic strain during drying shrinkage of P. euramericana tension wood
| Specimen 1 | Specimen 2 | |
|---|---|---|
| Lattice spacing (nm) | ||
| Water-saturated | 0.25820 | 0.25824 |
| Oven-dried | 0.25818 | 0.25814 |
| Strain (μm/m) | ||
| Lattice strain | −85 | −409 |
| Macroscopic strain | −8000/−10,000 | |
DISCUSSION
Macroscopic and lattice strain during maturation stress release
The values of lattice spacing found for the various tested samples confirmed the reliability of the experimental procedure, since they are consistent with usually reported values (e.g., Davidson et al. (35)), corresponding to a fiber repeat (distance of c axis) of 1.033 or 1.034 nm for wood samples, 1.035 nm for ramie and cotton, and 1.040 nm for algal cellulose.
The experiments performed at SPring8 show that during the release of wood maturation stress, a change in cellulose lattice spacing can be detected. The lattice strain was evaluated, and found to be the same order of magnitude as the macroscopic strain. The ratio of lattice strain to macroscopic longitudinal strain is 77% for the first log tested and 113% for the second log. The measurement of lattice and macroscopic strains of a wood sample submitted to external tensile stress (i.e., loaded in its longitudinal direction) was previously reported. For similar magnitude of macroscopic strain, the lattice/macroscopic strain ratio ranged approximately between 50% and 100% for Chamaecyparis obtusa (26,27,29).
Macroscopic and lattice strain during drying shrinkage
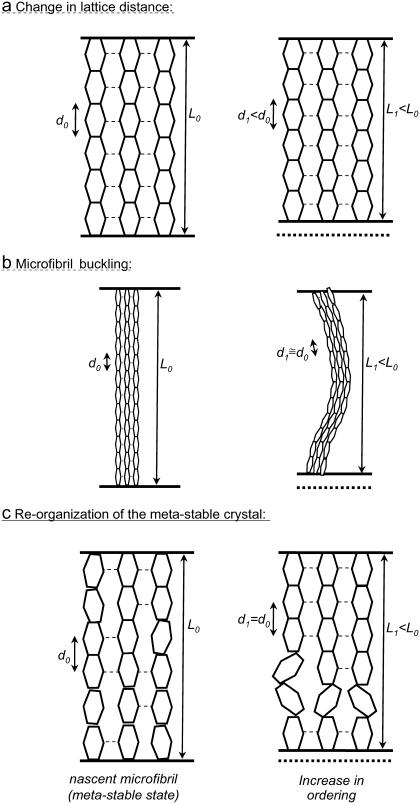
In the case of tension wood drying, the detected strain did not exceed some hundreds of microstrains. However, the longitudinal shrinkage of tension wood samples is usually several thousands of microstrains. If such a strain had occurred in the microfibrils, it should have been detected easily. Davidson et al. (35) report that they could not detect any significant strain during the drying of wood powder of Pinus radiata. They also outlined the fact that if this shrinkage had occurred at the level of cellulose microfibrils, it should have been detected. The behavior of the microfibrils during drying then seems to differ from its behavior during stress release, or when it is submitted to an external load either in wet or in dry state. To our knowledge, no explanation has to date been proposed for this fact, though it is important for the comprehension of wood behavior and micromechanics. We tentatively suggest that this difference could be due to the occurrence of some buckling of the microfibrils during drying shrinkage, which would not occur during the other kinds of strains. The phenomenon of “buckling” can be described as follows (Fig. 7 b): when a slender solid is submitted to axial compressive stress, it strains in compression as long as the stress does not exceed some critical value, above which the solid suddenly bends. Then, because of the effect of bending on the structure the distance between two points of the solid is reduced to a much larger extend than the strain inside the solid. In drying wood, the compressive stress imposed by the drying matrix on the microfibrils is very large, so that such a phenomenon is likely to occur. In addition, the matrix material strongly shrinks in the direction transverse to the microfibril, which tends to destabilize the microfibrils and to facilitate the occurrence of buckling. In the above-cited cases of wood submitted to external load, the applied stress was a tension, so that such a phenomenon could not occur anyway. The release of maturation tensile stress is equivalent to the application of an external compression, in the sense that it implies a contraction of wood. However, in this situation, buckling seems not to have occurred, according the large lattice strain recorded.
FIGURE 7.
Schematic drawings of possible shrinkage model of cellulose microfibril. L is representing the length of wood (or the longitudinal length of a microfibril) and d the fiber repeat distance, so that the macroscopic strain is (L1 − L0)/L0 and the lattice strain is (d1 − d0)/d0. Hexagons figure the asymmetric units and dashed lines correspond to the H-bondings system that bind molecules in lateral direction. (a) Lattice strain corresponds to the macroscopic strain (likely the maturation strain discussed in this work); b and c represent models that explain rather large deformation without lattice shrinkage such as during drying. (b) Microfibril buckling; (c) reorganization of the metastable crystal.
The metastable nature of native cellulose could be an alternative hypothesis to explain how the microfibril can be shortened without lattice spacing being changed (Fig. 7 c). Cellulose microfibrils are synthesized by fixed array of ordered synthases and polymerization and crystallization is believed to occur almost simultaneously from the thermodynamic consideration of formation of the extended cellulose chains (36). Such a mechanism tends to yield a structure distinguished by uniformity of lateral order along the fibrillar length axis with the lateral order being distorted. As a result, microfibrils are in metastable state being “frozen” in the unfavorable state intermolecularly. If, upon drying, crystallization or lateral ordering was promoted as suggested by diffraction studies (not shown here), in a way to create more distinct better and less ordered regions in a microfibril, it could be a cause of longitudinal contraction. Because the extended chain conformation is less stable and molecules tend to shrink if there is no lateral restriction. This might also be one of the reasons for the large longitudinal shrinkage during drying which does not accompany the shrinkage of crystal lattice.
Absolute values of the fiber repeat of native cellulose
Our measurements showed marked differences in lattice spacing between cellulose of various origins. Cellulose microfibrils are fibrous polymers consisting of different number of chains specific to the cellulose origins. The cellulose crystal of Cladophora having ∼20 nm (37), ramie of 6–8 nm, and wood of 3–4 nm in width, for instance, consist of more than 1200 chains, 100–150 chains, 30–40 chains, respectively. According to Davidson et al. (35), the differences in cellulose lattice spacing between these species would be related to an effect of crystal size. This would be related to the difference in hydrogen bonding pattern between cellulose chains located at the surface and inside of the crystal. In fact, recently refined structure of cellulose Iα and Iβ (38,39), cellulose II (40), and cellulose IIII (41) data are in perfect agreement with this concept. The fiber repeat distances of cellulose Iα and Iβ which accept hydroxyl methyl group at tg position, are 1.040 and 1.038 nm, whereas that of cellulose II and IIII whose hydroxyl methyl groups are at gt position is ∼1.036 and 1.031 nm, respectively. According to the NMR study of native celluloses, the conformation of hydroxyl methyl groups is known to be tg in the core and gt on the surface, respectively. Therefore, H-bonding pattern of surface chains implies a lower equilibrium lattice spacing than that of inner chains. As all chains are forced to the same lattice spacing because of lateral bonding, this spacing is intermediate between the equilibrium lattice spacing of inner and surface chains, and depends on the proportion of each kind of chain. The number of surface chains is proportional to the perimeter of the microfibril, whereas the number of inner chains is proportional to its lateral area, so that the ratio is submitted to a size effect.
As a result, the fiber repeat varies from 1.033 nm for wood to 1.040 nm for algal cellulose. These are equilibrium values, i.e., values for unstressed crystal. If the actual fiber repeat is changed and differs from this equilibrium value, a mechanical stress appears in the crystal. It is remarkable that the values we found for tension wood after the release of maturation stress is equal to conventional wood values, whereas the value before stress release is larger, corresponding to a fiber repeat of 1.035 nm, equal to that of cotton and ramie. An important question for understanding the mechanical role of cellulose in wood is: which one is the equilibrium value of tension wood cellulose?
If the equilibrium lattice distance is the same as in wood, then we can conclude that cellulose is in tension in situ, and is directly generating the maturation stress. Alternatively, if the fiber repeat distance is an equilibrium between surface and core molecules, it is indeed size dependent as reported by Davidson et al. (35). If the size of cellulose crystallite in tension wood is larger than that in normal wood as usually stated (for instance, 30 and 33), then tension wood should have a larger equilibrium lattice spacing than normal wood. Then, it would not be stressed in situ, and it would become compressed after the release of maturation stress. In this case, the origin of the maturation stress should be sought in another wood component than crystalline cellulose. For instance, the shrinkage of some noncrystalline material (disordered regions of cellulose or hemicellulose) could be involved.
CONCLUSION
To understand the mechanical state and function of cellulose microfibrils/crystallites in the tension wood, we have performed a crystallographic approach to compare the strains at molecular level to the macroscopic level. We have demonstrated experimentally for the first time that the fiber repeat distance of cellulose microfibrils/crystallites is larger in tension wood in situ than after the release of the maturation stress. Therefore, the contraction of the cellulose microfibrils/crystallites during the release of maturation stress was confirmed and it was as much as the macroscopic strain was.
However, it is still open whether cellulose microfibrils/crystallites in tension wood are generating the maturation stress. The alternative assumption is that they have a larger equilibrium fiber repeat distance, due to a larger crystal size. So far, though many studies were carried out to observe the width of cellulose microfibrils/crystallites in tension wood, values range between 2 and 7 nm depending on the technique and sample preparation (30–33). Therefore, it is prerequisite to increase the precision of the measurement. In addition, data on the size together with (004) spacing of wood cellulose which are crystallized under different physical or physiological condition would shed a light on a better understanding of cellulose structure and its mechanical state in wood.
Acknowledgments
The authors thank Prof. M. Wada, Dr. R. Hori, and Dr. K. Inoue for their assistance during synchrotron experiments, and Prof. F. Tanaka for the use of Rigaku x-ray generator. Thanks are also extended to Dr. Nogi, and Prof. Baba and Prof. Tsutsumi, for helping us to collect some of the Poplar specimens. First and second authors received postdoctoral fellowship from the Japanese Society for Promotion of Sciences.
This work was partly supported by a grant-in-aid for Scientific Research (14360099, 17580142) from the Japanese Society for Promotion of Sciences and the synchrotron experiment was performed at the BL40XL beam line, SPring8, Harima, Japan, with the approval of the Japan Synchrotron Radiation Research Institute (JASRI, proposal No. 2003B0463-NL2a-np, 2004A0036-NL2a-np).
This article is dedicated to deceased colleague Takashi Okuyama.
Bruno Clair's present address is Equipe Mécanique de l'Arbre et du Bois, Laboratoire de Mécanique et Génie Civil (LMGC), UMR 5508, CNRS-Université Montpellier 2, Place E. Bataillon, cc 048, 34095 Montpellier Cedex 5, France.
References
- 1.Archer, R. 1986. Growth stresses and strains in trees. E. Timell, editor. Berlin: Springer-Verlag.
- 2.Scurfield, G. 1973. Reaction wood: its structure and function. Science. 179:647–655. [DOI] [PubMed] [Google Scholar]
- 3.Fournier, M., H. Bailleres, and B. Chanson. 1994. Tree biomechanics: growth, cumulative pre-stresses and reorientations. Biomimetics. 2:229–252. [Google Scholar]
- 4.Wardrop, A. B. 1956. The nature of reaction wood. V. The distribution and formation of tension wood in some species of Eucalyptus. Aust. J. Sci. Res. Ser-B. Biol. Sci. 4:152–166. [Google Scholar]
- 5.Wardrop, A. B., and H. E. Dadswell. 1955. The nature of reaction wood. IV. Variations in cell wall organization of tension wood fibers. Aust. J. Sci. Res. Ser-B. Biol. Sci. 3:177–189. [Google Scholar]
- 6.Fisher, J., and J. Stevenson. 1981. Occurence of reaction wood in branches of Dicotyledons and its role in tree architecture. Bot. Gaz. 142:82–95. [Google Scholar]
- 7.Onaka, F. 1949. Studies on compression- and tension-wood. Wood Res. 1:1–88. [Google Scholar]
- 8.Araki, N., M. Fujita, H. Saiki, and H. Harada. 1983. Transition of fiber wall structure from normal wood to tension wood in certain species having gelatinous fibers of S1+G and S1+S2+S3+G types. Mokuzai Gakkaishi. 29:481–499. [Google Scholar]
- 9.Clair, B., J. Ruelle, and B. Thibaut. 2003. Relationship between growth stresses, mechano-physical properties and proportion of fibre with gelatinous layer in chestnut (Castanea sativa Mill.). Holzforschung. 57:189–195. [Google Scholar]
- 10.Washusen, R., J. Ilic, and G. Waugh. 2003. The relationship between longitudinal growth strain and the occurrence of gelatinous fibers in 10- and 11-year-old Eucalyptus globulus Labill. Holz als Roh- und Werkstoff. 61:299–303. [Google Scholar]
- 11.Fujita, M., H. Saiki, and H. Harada. 1974. Electron microscopy of microtubules and cellulose microfibrils in secondary wall formation of poplar tension wood fibers. Mokuzai Gakkaishi. 20:147–156. [Google Scholar]
- 12.Chaffey, I. 2000. Microfibril orientation in wood cells: new angles on an old topic. Trends Plant Sci. 5:360–362. [DOI] [PubMed] [Google Scholar]
- 13.Wada, M., T. Okano, J. Sugiyama, and F. Horii. 1995. Characterization of tension and normally lignified mood cellulose in Populus maximowiczii. Cellulose. 2:223–233. [Google Scholar]
- 14.Fournier, M., H. Bailleres, B. Thibaut, and D. Guitard. 1994. Mesure des d'formations residuelles de croissance? La surface des arbres, en relation avec leur morphologie. Observation sur differentes espaces. Ann. Sci. For. 51:249–266. [Google Scholar]
- 15.Yoshida, M., and T. Okuyama. 2002. Techniques for measuring growth stress on the xylem surface using strain and dial gauges. Holzforschung. 56:461–467. [Google Scholar]
- 16.Boyd, J. 1985. The key factor in growth stress generation in trees: lignification or crystallisation? IAWA Bulletin. 6:139–150.
- 17.Bamber, R. 1987. The origin of growth stresses: a rebuttal. IAWA Bulletin. 8:80–84.
- 18.Bamber, R. 2001. A general theory for the origin of growth stresses in reaction wood: How trees stay upright. IAWA J. 22:205–212. [Google Scholar]
- 19.Okuyama, T., H. Yamamoto, M. Yoshida, Y. Hattori, and R. Archer. 1994. Growth stresses in tension wood: role of microfibrils and lignification. Ann. Forest. Sci. 51:291–300. [Google Scholar]
- 20.Yamamoto, H. 1998. Generation mechanism of growth stresses in wood cell walls: roles of lignin deposition and cellulose microfibril during cell wall maturation. Wood Sci. Tech. 32:171–182. [Google Scholar]
- 21.Almeras, T., J. Gril, and H. Yamamoto. 2005. Modeling anisotropic maturation strains in wood in relation to fiber boundary conditions, microstructure and maturation kinetics. Holzforschung. 59:347–353. [Google Scholar]
- 22.Koyama, M., W. Helbert, T. Imai, J. Sugiyama, and B. Henrissat. 1997. Parallel-up structure evidences the molecular directionality during biosynthesis of bacterial cellulose. Proc. Natl. Acad. Sci. USA. 94:9091–9095. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Atalla, R. H., and D. VanderHart. 1984. Native cellulose: a composite of two distinct crystalline forms. Science. 223:283–285. [DOI] [PubMed] [Google Scholar]
- 24.Sugiyama, J., R. Vuong, and H. Chanzy. 1991. An electron diffraction study on the two crystalline phase occuring in native cellulose from algal cell wall. Macromolecules. 24:4168–4175. [Google Scholar]
- 25.Nishino, T., K. Takano, and K. Nakamae. 1995. Elastic modulus of the crystalline regions of cellulose polymorphs. J. Polym. Sci., Part B: Polym. Phys. 33:1647–1651. [Google Scholar]
- 26.Suzuki, M. 1968. Mechanical deformation of crystal lattice of cellulose in Hinoki wood. Mokuzai Gakkaishi. 14:268–275. [Google Scholar]
- 27.Moriizumi, S., and T. Okano. 1978. Viscoelasticity and structure of wood. IV. Behavior of crystal lattice strain depended on moisture content and time. Mokuzai Gakkaishi. 24:1–6. [Google Scholar]
- 28.Sobue, N., Y. Shibata, and T. Mizusawa. 1992. X-ray measurement of lattice strain of cellulose crystals during the shrinkage of wood in the longitudinal direction. Mokuzai Gakkaishi. 38:336–341. [Google Scholar]
- 29.Nakai, T., H. Yamamoto, and T. Nakao. 2005. The relationship between macroscopic strain and crystal lattice strain in wood under uniaxial stress in the fiber direction. J. Wood Sci. 51:193–194. [Google Scholar]
- 30.Harada, H., T. Taniguchi, and A. Kishi. 1971. Ultrastructure of the gelatinous layer in tension wood fibers from Populus euramericana. Bull. Kyoto Univ. For. No. 42:221–227.
- 31.Goto, T., H. Harada, and H. Saiki. 1975. Cross-sectional view of microfibrils in gelatinous layer of Poplar tension wood (Populus euramericana). Mokuzai Gakkaishi. 21:537–542. [Google Scholar]
- 32.Sugiyama, J., Y. Otsuka, H. Murase, and H. Harada. 1986. Toward direct imaging of cellulose microfibrils in wood. Holzforschung. 40:31–36. [Google Scholar]
- 33.Washusen, R., and R. Evans. 2001. The association between cellulose crystallite width and tension wood occurrence in Eucalyptus globules. IAWA J. 23:235–243. [Google Scholar]
- 34.Skaar, C. 1988. Wood-Water Relations. Berlin, Heidelberg, New York: Springer-Verlag.
- 35.Davidson, T., R. Newman, and M. Ryan. 2004. Variations in the fibre repeat between samples of cellulose I from different sources. Carbohydr. Res. 339:2889–2893. [DOI] [PubMed] [Google Scholar]
- 36.Stockmann, V. 1972. Developing a hypothesis: native cellulose elementary fibrils are formed with metastable structure. Biopolymers. 11:251–270. [Google Scholar]
- 37.Imai, T., and J. Sugiyama. 1988. Nanodomains of Iα and Iβ cellulose in algal microfibrils. Macromolecules. 31:6275–6279. [Google Scholar]
- 38.Nishiyama, Y., P. Langan, and H. Chanzy. 2002. Crystal structure and hydrogen-bonding system in cellulose Iβ from synchrotron x-ray and neutron fiber diffraction. J. Am. Chem. Soc. 124:9074–9082. [DOI] [PubMed] [Google Scholar]
- 39.Nishiyama, Y., J. Sugiyama, H. Chanzy, and P. Langan. 2003. Crystal structure and hydrogen bonding system in cellulose Iα from synchrotron x-ray and neutron fiber diffraction. J. Am. Chem. Soc. 125:14300–14306. [DOI] [PubMed] [Google Scholar]
- 40.Langan, P., Y. Nishiyama, and H. Chanzy. 1999. A revised structure and hydrogen-bonding system in cellulose II from a neutron fiber diffraction analysis. J. Am. Chem. Soc. 121:9940–9946. [Google Scholar]
- 41.Wada, M., H. Chanzy, Y. Nishiyama, and P. Langan. 2004. Cellulose IIII crystal structure and hydrogen bonding by synchrotron x-ray and neutron fiber diffraction. Macromolecules. 37:8548–8555. [Google Scholar]