Vulnerable Window for Conduction Block in a One-Dimensional Cable of Cardiac Cells, 1: Single Extrasystoles

Abstract

Spatial dispersion of refractoriness, which is amplified by genetic diseases, drugs, and electrical and structural remodeling during heart disease, is recognized as a major factor increasing the risk of lethal arrhythmias and sudden cardiac death. Dispersion forms the substrate for unidirectional conduction block, which is required for the initiation of reentry by extrasystoles or rapid pacing. In this study, we examine theoretically and numerically how preexisting gradients in refractoriness control the vulnerable window for unidirectional conduction block by a single premature extrasystole. Using a kinematic model to represent wavefront-waveback interactions, we first analytically derived the relationship (under simplified conditions) between the vulnerable window and various electrophysiological parameters such as action potential duration gradients, refractoriness barriers, conduction velocity restitution, etc. We then compared these findings to numerical simulations using the kinematic model or the Luo-Rudy action potential model in a one-dimensional cable of cardiac cells. The results from all three methods agreed well. We show that a critical gradient in action potential duration for conduction block can be analytically derived, and once this critical gradient is exceeded, the vulnerable window increases proportionately with the refractory barrier and is modulated by conduction velocity restitution and gap junctional conductance. Moreover, the critical gradient for conduction block is higher for an extrasystole traveling in the opposite direction from the sinus beat than for one traveling in the same direction (e.g., an epicardial extrasystole versus an endocardial extrasystole).

INTRODUCTION

Sudden cardiac death is most commonly due to ventricular fibrillation, which is characterized by multiple wavelets arising from an initial single or a figure-of-eight reentrant circuit (1–4). From a therapeutic standpoint, the most critical issue is how reentry is first initiated, and, more specifically, what controls the vulnerable window for its initiation by premature extrasystoles or rapid heart rates, the common physiological triggers for reentry. Initiation of reentry requires unidirectional conduction block of a propagating excitation wave. The vulnerable window describes the temporal window within which unidirectional conduction block or reentry can be induced by premature extrasystoles from a given spatial location.

Reentry can be initiated, even in homogeneous tissue, if a critical tissue area is depolarized in the refractory phase of the previous excitation, either by a point electrode with very high current strength or by stimulation of a large region with barely suprathreshold current strength (1–7). However, if the tissue is heterogeneous, reentry can be induced by a point electrode with stimulation strength just above the threshold when the dispersion of refractoriness is sufficiently large or if unexcitable obstacles are present (8–14). Dispersion of refractoriness naturally exists in the heart (15,16) and is amplified in heart disease by electrical remodeling (8,17,18). It can also be induced or modulated by extrasystoles or heart rate (15,16,19–22), by dynamically induced discordant alternans (19,23–26), by nonuniform cell coupling (12,27,28), and by unexcitable obstacles (29,30).

In normal guinea pig hearts in the presence of anatomic obstacles, Laurita and Rosenbaum (30) found that a minimum repolarization gradient of 3.2 ms/mm was required for unidirectional conduction block to occur. Akar and Rosenbaum (17) showed that polymorphic ventricular tachycardia could only be induced when the transmural action potential duration (APD) gradient was >10 ms/mm in failing dog hearts. Restivo et al. (18) showed that conduction block occurred at refractory gradients from 10 ms/mm to 120 ms/mm in subacute myocardial infarction. In a theoretical study, Sampson and Henriquez (28) analytically estimated the minimum gradient of APD required for unidirectional conduction block in a one-dimensional (1D) cable of coupled cardiac cells and showed that this minimum APD gradient was determined solely by conduction velocity (CV) restitution. Computer simulations of two-dimensional (2D) tissue (12,13) showed that the vulnerable window for reentry increased as the difference in APD or effective refractory period (ERP) between two regions. However, how cell properties interact with tissue properties to determine the size of the vulnerable window has not been systematically analyzed. In this study, we use theoretical analysis and numerical simulation to investigate how preexisting gradients in refractoriness, coupled with CV restitution properties, affect the vulnerability to conduction block of a single extrasystole in a 1D cable of coupled cells. First, we develop a kinematic equation and obtain analytical solutions under simplified conditions. We then simulate an ionic model in a 1D cable to compare the results with those from the kinematic theory. In this article, we focus on the vulnerability to conduction block of a single extrasystole; in the companion paper (31), we extend the analysis to multiple extrasystoles.

METHODS

Mathematical model

We simulated a 1D cable using Phase I of the Luo and Rudy (LR1) ventricular action potential model (32):

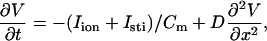(1)

where V is the transmembrane potential, I_ion is the total ionic current density from the LR1 model, and D is the diffusion constant, set to 0.001 cm²/ms. For the homogeneous cable, we used Na⁺ channel conductance 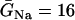mS/cm² and the slow-inward current or the L-type Ca²⁺ channel conductance 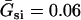mS/cm². We also sped up the L-type Ca²⁺ channel activation and inactivation by decreasing the time constants τ_d and τ_f to 75%, i.e., τ_d→0.75 τ_d and τ_f→0.75 τ_f. These modifications resulted in a baseline APD of 200 ms and APD restitution steepness close to experimental measurements in rabbit hearts (33). Slow recovery of the Na⁺ channel was simulated by increasing the time constant of the j gate in the LR1 model, e.g., a fivefold slowing of recovery is achieved by increasing τ_j fivefold as τ_j→5 τ_j. Other parameters are the same as in the original LR1 model. Action potential heterogeneity was simulated by creating a gradient in the maximum conductance of the time-dependent K⁺ channel, i.e., 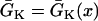. For the case of ascending APD gradient, it is defined as

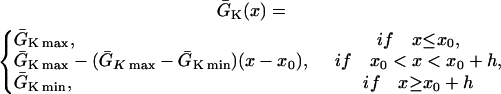(2)

where we set x₀ = (L − h)/2. In this study, we used a cable length L = 40 mm and h was chosen to be 10 mm. For the descending case, Eq. 2 was used with 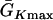and 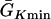exchanged. In this study, 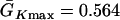mS/cm² was fixed and 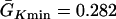mS/cm² was used unless otherwise specified. I_sti in Eq. 1 is the stimulation current density of the stimuli (S1 and S2), which were applied in a 1 mm segment of the cable with strength being −30 μA/cm² and duration being 2 ms. S1 was the baseline stimulation and always applied at the left end of the cable with cycle length 1 s, whereas the extrasystole (S2) was applied at different location. Equation 1 was integrated using the explicit Euler method with a time step 0.005 ms and a space step Δx = 0.0125 cm.

CV and CV restitution

CV was measured in the cable by calculating the time ΔT for the wavefront propagating from x − Δx to x + Δx, defining 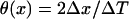. The waveback velocity Θ(x) was similarly calculated. CV restitution curves were obtained by plotting CV versus diastolic interval (DI) measured at the middle of the cable. It was difficult to obtain the critical CV (θ_c) in a homogeneous cable, and so it was calculated in a heterogeneous cable (APD heterogeneity was the same as in Fig. 2 A) for an S1S2 coupling interval at which S2 wave successfully propagated through the cable, but conduction failed for a 1 ms shorter S1S2 interval. The minimum θ detected in the cable for this S1S2 interval was defined as θ_c.

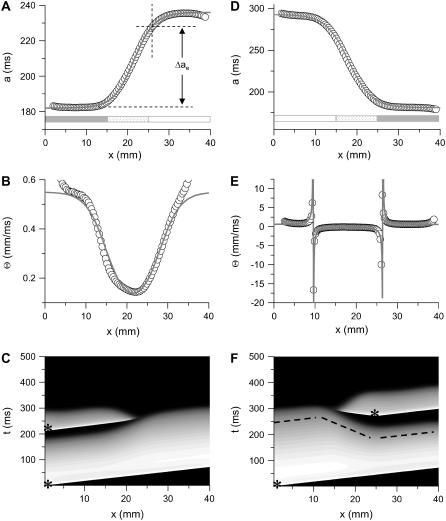
FIGURE 2.

APD distribution in space and waveback velocity from a heterogeneous 1D cable of the LR1 model (symbols in each panel) under the baseline (S1) stimulation. (A) APD distribution for an ascending gradient in space (symbols), which was fit by 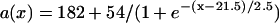(line). The shaded bar marks the region with high 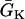, open bar for low 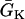, and 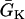changes linearly as in Eq. 2 in the patterned bar region. The dashed lines illustrate the calculation of Δa_e, the effective refractory barrier used for Eqs. 9 and 10. The intersection of the vertical dashed line and the top one is the point with the critical APD gradient for conduction block. (B) Waveback velocity measured from the cable for the APD heterogeneity in A (○) and calculated using Eq. 5 with the fitting function in A (line). (C) Time-space plot showing conduction block of S2 beat in the cable with ascending APD gradient as in A. Voltage changes from −85 mV to 20 mV as color changes from black to white. The stars mark the time and location at which S1 and S2 were given. (D) APD distribution for a descending gradient fitted by 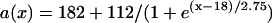. 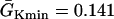mS/cm² was used in Eq. 2. (E) Waveback velocity for the heterogeneity in D. The line was calculated using Eq. 5 with the fitting function in D. (F) Time-space plot showing conduction block of S2 beat in the cable with descending APD gradient as in D. Voltage changes from −85 mV to 20 mV as color changes from black to white. The stars mark the time and location at which S1 and S2 were given. The negative slope portion of the dashed line marks the retracting waveback or the negative waveback velocity portion.

APD and ERP

APD was defined as the duration of transmembrane voltage V > −72 mV and DI as the duration of V < −72 mV. ERP was also measured in the cable as follows: an S1 pacing train was followed by a premature S2 to determine ERP. ERP was defined as the shortest S1S2 interval such that the S2 propagated successfully through the cable.

RESULTS

Kinematic theory

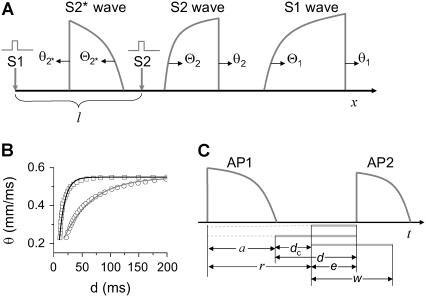
We assume that a premature extrasystole S2 occurs after a normal S1 beat, which causes two waves propagating in the opposite directions (the S2 wave and S2* wave in Fig. 1 A). The S1 beat, such as the sinus beat, occurs at a long cycle length so that APD and CV are at their baseline values. The CV of the S2 wave is a function of its previous DI, i.e., the CV restitution function

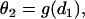(3)

where d₁ is the DI preceding the S2 wave, and θ₂ is the CV of the S2 wave. Fig. 1 B shows two CV restitution curves obtained from the 1D cable with the LR1 model, which can be fit by

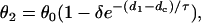(4)

where θ₀ is the baseline CV (i.e., CV at the infinite DI), and δ and τ are two positive parameters, with δ measuring the varying range of CV and τ measuring the slope of CV restitution. d_c is the critical DI at which CV reaches a critical velocity 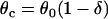and the S2 wave begins to fail. Fig. 1 C illustrates the relations between the various electrophysiological quantities.

FIGURE 1.

(A) schematic illustration of the S1 and S2 stimulation in a 1D space. S1 is always applied at x = 0, but S2 is applied at location l, which stimulates two opposite propagating waves (the S2 wave and S2* wave). θ is the wavefront velocity and Θ is the waveback velocity. (B) CV versus DI for normal Na⁺ current (□), which was fit by 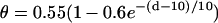(line), and CV versus DI for fivefold slowed recovery of Na⁺ channel (○), which was fit by 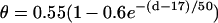(line). (C) Graphical definitions of APD (a), DI (d), and critical DI (d_c); refractory period (r), excitable gap (e), and vulnerable window (w). Note that the refractory period can be either shorter or longer than APD under normal conditions, which depends on how APD is defined. In the case of postrepolarization refractoriness, the refractory period is much longer than APD. With our APD definition in this study, the refractory period is longer (between 10 ms and 20 ms) than APD.

Due to heterogeneity in repolarization and refractoriness, the waveback and wavefront can propagate at different velocities, whose relationship can be deduced as follows: the time for the waveback to propagate a small distance Δx is Δx/θ(x) (the time it takes the wavefront to propagate this same distance, plus the APD difference [Δa(x) = a(x + Δx) − a(x)], i.e., Δa(x) + Δx/θ(x). Therefore, the waveback velocity Θ₁ of the S1 wave is

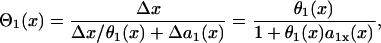(5)

where 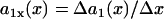is the spatial APD gradient of the S1 wave. A similar equation was originally derived by Courtemanche (34) and then modified into the form of Eq. 5 (19,28). In Eq. 5, we define the waveback as the repolarization front. Alternatively, if one defines the waveback as the refractory front, then APD gradient in Eq. 5 is replaced by ERP gradient. From Eq. 5, for an APD gradient a_1x > 0, (i.e., APD increases along the direction of propagation), then Θ₁(x) < θ₁(x). That is, the waveback propagates more slowly than the wavefront, so that the wavelength [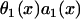] increases as the wave propagates. If , then Θ₁(x) > θ₁(x), i.e., the waveback propagates faster than the wavefront does. If 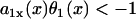, then Θ₁(x) < 0 < θ₁(x). This case results in a retracting waveback that propagates in the opposite direction of the wavefront (see ). A special case occurs when 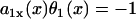, such that the waveback velocity becomes infinite. In this case, the spatial gradient in refractoriness cancels out the repolarization time difference due to propagation, resulting in simultaneous recovery in space. Another special case is at the limit of θ₁(x) being infinite, or every cell is excited simultaneously, Θ₁(x) = 1/a_1x, which is finite. Therefore, with a spatial gradient of repolarization or refractoriness, the waveback velocity can be very different from the wavefront velocity. Fig. 2 A shows an ascending APD gradient created by introducing a gradient in the K⁺ current conductance 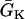(Eq. 2) and under the baseline (S1) stimulation, which can be fit by

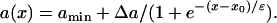(6)

Fig. 2 D shows a descending APD gradient fit by

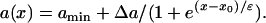(7)

In Eqs. 6 and 7, 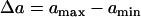. The repolarization distribution from apex to base measured in the epicardial surface of guinea pig hearts with Long-QT syndrome was also well fit by Eq. 6 (22). Fig. 2, B and E, show the waveback velocity Θ(x) due to the two types of heterogeneities measured from the simulation of the 1D cable using the LR1 model (symbols) and calculated using Eq. 5 with a(x) from Eqs. 6 and 7 (lines). For the descending APD gradient, the waveback velocity becomes negative in the region of the gradient. In this case, a repolarization front propagates in the negative x direction due to the descending gradient (Fig. 2 F), which corresponds to the negative velocity region shown in E.

After applying S2, the DI in space is governed by the following differential equation (see Appendix for derivation):

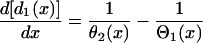(8)

with the initial condition 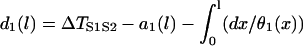. This type of kinematic equation has been used by a number of authors to study spatially discordant alternans and conduction block (19,25,28,29,35–37). Equation 8 cannot be analytically solved in general, since both θ₂(x) and Θ₁(x) are nonlinear functions of x, but it can be solved if θ₂(x) is determined by Eq. 4 and a(x) is a piecewise linear function (Fig. 3, A and B). In this case, we can analytically derive the vulnerable window (w) for S2 at large w (see Appendix). For an ascending APD gradient and S2 applied at x = x₀ (Fig. 3 A), w satisfies (from Eq. A17 in the Appendix)

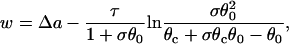(9)

where 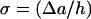. For a descending APD gradient and S2 applied at x = x₀ + h (Fig. 3 B), S2 may be blocked by running into the repolarization front propagating in the negative x direction (Fig. 2 E), and w satisfies (from Eq. A21 in the Appendix)

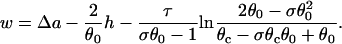(10)

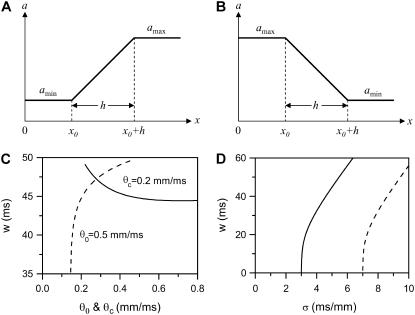
FIGURE 3.

(A and B) Schematics of a piecewise linear ascending and descending APD gradient that were used for the derivation of Eqs. 9 and 10. (C) w versus θ₀ when θ_c = 0.2 ms/mm (solid line) and w versus θ_c when θ₀ = 0.5 ms/mm (dashed line) for the ascending case obtained using Eq. 9. τ = 10 ms, σ = 5 ms/mm, and h = 10 mm were used. (D) w versus σ for the ascending (Eq. 9, solid line) and descending (Eq. 10, dashed line) cases. τ = 10 ms, θ₀ = 0.5 mm/ms, θ_c = 0.2 mm/ms, and h = 10 mm were used.

From Eqs. 9 and 10 (also see Fig. 3), we have the following observations:

1. The vulnerable window w is proportional to the refractory barrier (Δa) in the ascending case when the gradient in refractoriness σ is fixed and exceeds a critical value (see Eq. 11 below for the critical value), but also depends on h in the descending case (see Appendix for detailed spatial dependence of w).

2. Increasing the steepness of the spatial gradient (σ) increases the vulnerable window (Fig. 3 D).

3. Broadening the sloped region of the CV restitution curve (increasing τ) decreases the vulnerable window.

4. Decreasing the wavefront velocity (θ₀) or increasing the critical velocity for conduction failure (θ_c) increases the vulnerable window (Fig. 3 C).

A minimal APD gradient for conduction block can be obtained from Eq. 5 or Eqs. 9 and 10. For conduction block of the S2 wave to occur, the waveback velocity of the S1 wave must be smaller than the critical velocity, i.e., Θ₁ < θ_c. When the S1 and S2 waves propagate in the same direction, we obtain from Eq. 5 that

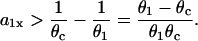(11)

This relation can also be derived from Eq. 9 by setting θ₁ = θ₀, since 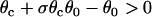is required. For normal conduction, θ₁ = θ₀ is ∼0.5 mm/ms and θ_c is ∼0.2 mm/ms, which gives rise to a minimum APD gradient of 3 ms/mm for unidirectional conductional block to occur (Fig. 3 D). Note that a similar equation has been used by Sampson and Henriquez (28) to estimate the minimum APD gradient required for conduction block in 1D cables of coupled cardiac cells.

When the S1 and S2 waves propagate in the opposite directions, we obtain from Eq. 5 or Eq. 10:

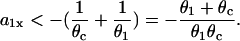(12)

In this case, the minimum APD gradient required is much larger than for the other case, for example, for θ₁ = 0.5 mm/ms and θ_c = 0.2 mm/ms, it is 7 ms/mm (Fig. 3 D).

Numerical simulations

To validate the kinematic equations and relate their phenomenological parameters to biological parameters (e.g., ion channel properties), we numerically simulated the LR1 model in a 1D cable (Eq. 1) and compared the results to those of the kinematic model (Eq. 8).

Vulnerability due to APD heterogeneity

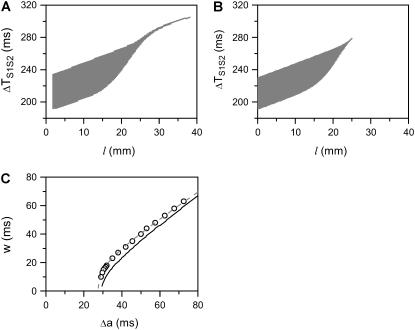
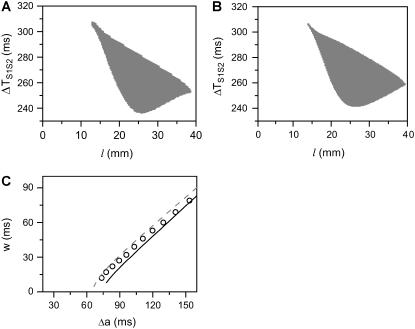
Fig. 4, A and B, show the vulnerable windows w (shaded areas) versus S2 location l, using the ionic model (Eq. 1) and the kinematic model (Eq. 8), respectively, for the ascending APD gradient shown in Fig. 2 A. The vulnerable window from the ionic model agrees well with that from the kinematic model except for l > 25.5 mm. In the kinematic model, w becomes zero at 25.5 mm, at which the waveback velocity Θ₁ = θ_c. When x > 25.5 mm, the APD gradient becomes small so that Θ₁ > θ_c and thus w becomes zero. However, in the ionic model, due to the finite size of the stimulus electrode, a small w (3–5 ms) persists for l > 25.5 mm. Vulnerability due to finitely sized electrodes in homogenous 1D cables has been studied by Starmer et al. (38,39) and others (40). Fig. 4 C shows w versus Δa from the simulation of the ionic model (symbols), the kinematic model Eq. 8 (solid line), and Eq. 9 (dashed line) for S2 applied at location x₀, which agree well with each other. Fig. 5 shows the same analysis for a descending APD gradient. In this case, the shape of the vulnerable window (Fig. 5, A and B) is very different from the one in the ascending case (Fig.4, A and B), in addition to requiring a higher APD gradient. In the ascending case, the vulnerable window is almost unchanged when S2 is applied in any location in the region of the short APD (the shaded bar region in Fig. 2 A), but in the descending case, w depends on the S2 location even in the short APD region (the shaded bar region in Fig. 2 D). Fig. 5 C shows w versus Δa from the simulation of the ionic model (symbols), the kinematic model Eq. 8 (solid line), and Eq. 10 (dashed line) for an S2 applied at location x₀ + h. The results agree well, as in the ascending APD gradient case shown in Fig. 4 C.

FIGURE 4.

Effects of APD gradient on conduction block when APD gradient is ascending. (A) Vulnerable window w (shaded, the range of the S1S2 coupling interval 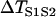that conduction block occurs) versus the location l of the S2 extrasystole obtained from the ionic model (Eq. 1). The APD distribution is the same as in Fig. 2 A. (B) Same as A but obtained from the kinematic simulation (Eq. 8). (C) Vulnerable window w versus the APD difference Δa from the ionic model (symbol), the kinematic simulation (solid line), and Eq. 9 (dashed line) for S2 applied at l = 0. In simulation of the ionic model, Δa was generated by varying 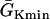in Eq. 2. In the kinematic simulation, 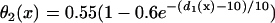, , 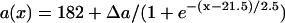and d_c=10 ms (at which θ_c = 0.22 mm/ms) were used. For Eq. 9, θ₀ = 0.55 mm/ms, θ_c = 0.22 mm/ms, τ = 10, h = 10 mm, and an effective APD difference Δa_e = 0.9Δa was used. Δa_e was the effective APD barrier as illustrated in Fig. 2 A.

FIGURE 5.

Effects of APD gradient on conduction block when APD gradient is descending. (A) Vulnerable window w (shaded, the range of the S1S2 coupling interval 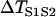that conduction block occurs) versus the location l of the S2 stimulus obtained from the ionic model (Eq. 1). APD heterogeneity was the same as in Fig. 2 D. (B) Same as A but obtained from the kinematic simulation (Eq. 8). (C) Vulnerable window w versus the APD difference Δa from the ionic model (symbol), the kinematic simulation (solid line), and the solution of Eq. 10 (dashed line) for S2 applied at l = 25 mm. In simulation of the ionic model, Δa was generated by varying 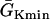in Eq. 2. In kinematic simulation, 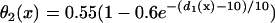, , 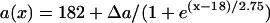and d_c=10 ms (at which θ_c = 0.22 mm/ms) were used. For Eq. 10, θ₀ = 0.55 mm/ms, θ_c = 0.22 mm/ms, τ = 10, h = 10 mm, and Δa_e = 0.8Δa were used. Δa_e was the effective APD barrier as illustrated in Fig. 2 A.

Vulnerability due to ERP heterogeneity

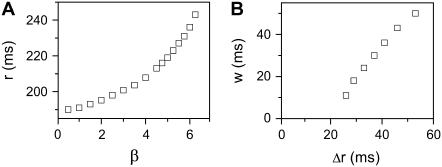
In the cases shown in Figs. 4 and 5, APD is a reliable measure of the refractory period, since excitability changed only slightly across space. In real cardiac tissue, APD and refractory period distribution in space may differ substantially if postrepolarization refractoriness is present, such as in ischemia or drug toxicity (8,41). Here, we simulate a case in which APD is almost uniform, but ERP changes over space, due to a gradient in Na⁺ conductance and recovery kinetics. Since changing Na⁺ channel kinetics has a small effect on APD (12), APD is almost uniform whereas ERP changes significantly in space. Fig. 6 A shows ERP versus the change of Na⁺ current conductance and recovery kinetics. Fig. 6 B shows that w is proportional to Δr, similar to the case of the APD gradient in Fig. 4.

FIGURE 6.

Effects of ERP heterogeneity on vulnerability. (A) ERP versus β. β is a parameter that measures the change in Na⁺ conductance and recovery, which is defined as in B. (B) w versus the ERP difference Δr for S2 applied at l = 0. The ERP gradient was generated by linearly changing 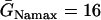to 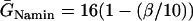mS/cm², and 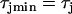to 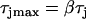in a region h = 10 mm, in the same manner as Eq. 2. Uniform 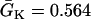mS/cm² was used. Since Na⁺ kinetics has a small effect on APD but a big effect on ERP (as shown in A), the APD distribution in the cable is almost uniform but large ERP gradient occurs.

Effects of Na⁺ current conductance and recovery kinetics

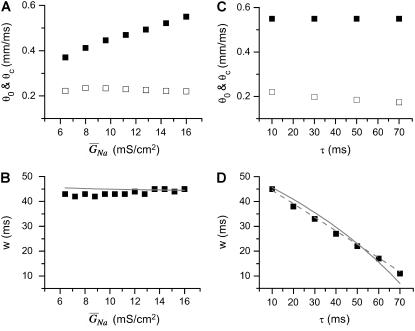
In the kinematic model, the properties of CV, such as the slope of CV restitution (τ), baseline CV (θ₀), and critical CV (θ_c), can be independently varied. In the ionic model, these properties cannot be independently varied. Since CV and its restitution are mostly controlled by the Na⁺ current properties, we altered the Na⁺ current conductance and recovery kinetics to study the effects of CV on vulnerability to conduction block. We altered these properties uniformly in space, with the spatial APD heterogeneity as in Fig. 2 A. Reducing the Na⁺ current conductance decreased θ₀, but had little effect on θ_c (Fig. 7 A) or the vulnerable window (Fig. 7 B), as predicted by Eq. 9 (line). In contrast, slowing recovery slightly decreased θ_c (Fig. 7 C), but substantially altered the vulnerable window (Fig. 7 D). The almost linear relation between the vulnerable window and the recovery time was also predicted by the analytical solution (Eq. 9).

FIGURE 7.

Effects of Na⁺ channel conductance and recovery on vulnerability to conduction block in heterogeneous cable with the heterogeneity as in Fig. 2 A. (A) θ₀ and θ_c versus 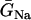. (B) Vulnerable window w versus 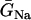. (C) θ₀ and θ_c versus τ. (D) Vulnerable window w versus τ. In D, the dashed line was obtained from Eq. 9 by using σ = Δa/h = 5 ms, θ₀ = 0.55 mm/ms, and θ_c = 0.2 mm/ms. The solid line was obtained by accounting the correction of θ_c shown in (C). S2 was applied at l = 0.

Effects of gap junctional conductance

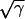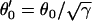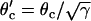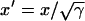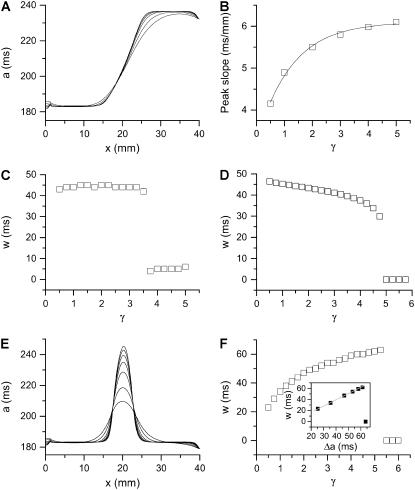
CV can also be altered by changing gap junctional conductance between cells, corresponding to the diffusion constant in our ionic model (Eq. 1). In homogeneous tissue, a γ-fold reduction in gap junctional conductance resulted in a -fold reduction in CV, i.e., , and also , since Eq. 1 can be rescaled in space by . In a heterogeneous tissue with an APD gradient given by Eq. 2, CV is only slightly affected so that the scaling for CV can still hold approximately. However, the scaling for the APD gradient, i.e., 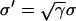, cannot hold and therefore the vulnerable window may change due to the change of gap junctional conductance based on Eqs. 9 and 10. We first studied the case in which APD gradient is generated by Eq. 2 with different gap junctional coupling strength. Fig. 8 A shows APD versus x for different fold (γ) reduction in gap junctional conductance and Fig. 8 B shows the peak slope of APD gradient for different γ, showing that the peak gradient tends to saturate as γ increased, instead of being proportional to 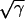. Fig. 8 C shows w versus γ from the simulation of the 1D cable with the LR1 model, in which w is insensitive to γ before a critical value at which w becomes zero. Using a functional relation of σ versus γ as in Fig. 8 B and the rescaled θ₀ and θ_c for Eq. 9, we obtain similar results to the ionic model, as shown in Fig. 8 D. We also simulated another case in which APD is longer in a 0.5 cm segment in the middle of the cable than at the two ends. In this case, the maximum APD increases as cell coupling decreases (Fig. 8 E). As a consequence, w increases as γ increases until a critical value at which no conduction block is caused by the heterogeneity (Fig. 8 F). The inset of Fig. 8 F shows w versus 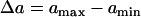, showing a good linear relation until the critical gap junctional conductance is reached, at which w becomes zero. Therefore, uniformly decreasing gap junctional conductance may increase or have no effect on vulnerable window until it is reduced to a critical value at which vulnerability to conduction block disappears. This seems to be contrary to intuition since decreasing gap junctional conductance increases dispersion of heterogeneity (42).

FIGURE 8.

Effects of gap junctional conductance on vulnerability to conduction block. (A) APD distribution in space for the different diffusion constants (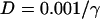 cm²/ms in Eq. 1, from lowest curve to top: γ = 0.5, 1, 2, 3, 4, and 5) under baseline (S1) stimulation. (B) Maximum gradient versus γ for the APD distribution in A. (C) w versus γ from the 1D cable of the LR1 model (Eq. 1). (D) w versus γ from Eq. 9 in which Δa = 50 ms, 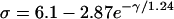, τ = 10 ms, 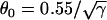mm/ms, and 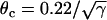mm/ms were used. (E) APD distribution in space for different diffusion constants (from lowest curve to top: γ = 0.5, 1, 2, 3, 4, 5, and 6). APD heterogeneity was generated by setting 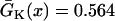mS/cm² except in a 5 mm segment in the middle of the cable, in which 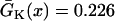mS/cm². (F) w versus γ from the 1D cable of the LR1 model with the heterogeneity in E. The inset shows w versus Δa. S2 was applied at l = 0.

DISCUSSION

Unidirectional conduction block caused by dispersion of refractoriness is a necessary, although not sufficient, condition required to induce reentry, and its theoretical underpinnings are therefore of critical importance to our understanding of cardiac arrhythmogenesis. In this study, we combined theoretical analysis and numerical simulation to investigate the factors that control the vulnerability to conduction block in a 1D cable of coupled cells. We quantitatively linked the refractory gradient and barrier and CV restitution slope to the vulnerable window of conduction block of waves induced by a single extrasystole. Results from the kinematic theory agree well with the numerical simulations using the LR1 ionic model in a 1D cable of coupled cells. Our major findings are:

1. A critical gradient in refractory period is required for unidirectional conduction block of waves induced by a premature extrasystole. The critical gradient is determined by the wavefront CV and the critical CV below which conduction fails.

2. The vulnerable window is proportional to the refractory barrier once the gradient is greater than the critical gradient.

3. The propagation direction of a premature extrasystole, i.e., whether in the same or opposite direction relative to the preceding wave, has a significant influence on the critical gradient required for unidirectional conduction block.

4. Increased CV restitution slope decreases the vulnerable widow for conduction block.

Dispersion of refractoriness

A close association between dispersion of refractoriness and cardiac arrhythmias has been demonstrated experimentally (17,22,43,44). Minimum repolarization gradients for conduction block were experimentally measured in normal tissue (30) and after myocardial infraction (18,45). The minimum repolarization gradients estimated analytically by Sampson and Henriquez (28) and by us in this study agree well with the experimental measurements of 3.2 ms/mm in the normal tissue (30), but are much less than 10 ms/mm observed in postinfarction setting (18) and heart failure (17). One explanation for this difference is that in postinfarct tissue and heart failure, the cell coupling strength is substantially reduced due to gap junctional remodeling (46,47), which increases the critical gradient for conduction block, as we showed in Fig. 8. Another finding from our study is that the analytical results (Eqs. 9 and 10) obtained in the case of piecewise linear APD gradient agree well with the results from numerical simulation of the kinematic equation and the ionic model (Figs. 4 C, 5 C, 7 B, and 7 D), suggesting that once the minimum gradient is reached, the refractory barrier determines the vulnerable window, whereas the specific spatial profile of the heterogeneity may be unimportant. The existence of a critical gradient for conduction block may serve to protect against initiation of lethal arrhythmias by single premature extrasystole, since even normal heart contains electrophysiological heterogeneity (15,44,48-50). However, as will be shown in the companion article, in the setting of multiple extrasystoles (16,20) or very rapid heart rates inducing spatially discordant alternans (23,25,35,37,51), large refractory gradients and barriers may be dynamically induced that are large enough to cause unidirectional conduction block by additional extrasystoles, even in normal hearts.

Arrhythmogenicity of endocardial versus epicardial extrasystoles

With respect to arrhythmogenesis in the real heart, a potentially important observation in the study presented here is the dependence of the vulnerable window on the stimulation sequence and location (Figs. 3–5). In real hearts, an extrasystole originating from either endocardium or epicardium faces an ascending APD gradient as it propagates into the midmyocardial layer, which has a longer APD than either the epicardial and endocardial layers (15,50), Since the activation sequence during sinus rhythm typically proceeds from endocardium to epicardium, an interesting prediction of our study is that a single endocardial extrasystole arising from the endocardium (i.e., traveling in the same direction) will need a much lower critical gradient than a single extrasystole originating from the epicardium (i.e., traveling in the opposite direction). It should also be noted that the APD gradient from epicardium to midmyocardium is usually larger than that from endocardium to midmyocardium (50,52), which could increase the probability of block of an extrasystole originating in the epicardium. Based on Eqs. 11 and 12, the difference in critical gradient is 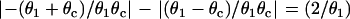, which is independent of the critical CV (θ_c). For 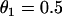mm/ms, the difference in the critical gradient is 4 ms/mm, as shown in Fig. 3 D. This difference increases as conduction velocity becomes slower. In addition to the difference between epicardium and endocardium, induction of reentry in the epicardial border zone in the postmyocardial infarction setting may also depend on the stimulation sequence and location of the extrasystoles. It will be interesting to test these theoretical predictions experimentally.

The role of CV restitution

We find that CV restitution tends to protect an extrasystole from unidirectional conduction block. Since the critical refractory gradient for conduction block is proportional to the difference between the CV of the previous wavefront and the minimum CV (Eq. 11), less APD gradient is needed for conduction block for slower CV, i.e., slowing CV promotes conduction block. For example, during rapid pacing and reentry of a “mother rotor”, in which the waves propagate much slower than in sinus rhythm, the critical gradient required for conduction block is much smaller, based on Eq. 11. However, CV restitution has been shown to play an important role in the formation and maintenance of discordant alternans (19,24,25), in which case CV restitution tends to promote dispersion of refractoriness for conduction block.

Limitations

We used a relatively simplified action potential model, which does not include all of the important ionic currents or a detailed treatment of intracellular Ca cycling. However, the main goal of this study was to create a theoretical framework for understanding unidirectional conduction block, in which phenomenological parameters could be related to biological entities as a crude test of accuracy, rather than to provide a detailed analysis of how specific ion channels and other proteins are involved in this process. In addition, we focused our analysis on unidirectional conduction block, which is necessary, but not sufficient, for the initiation of reentry in 2D and 3D tissue. For reentry to form in 2D tissue, other requirements must be satisfied (3,4), which may result in a different vulnerable window than that for unidirectional conduction block in 1D tissue, even if the same refractory gradient is assumed. For example, for a typical figure-of-eight reentry pattern to occur in 2D, the two spiral tips have to form at a critical separation distance to avoid mutual annihilation. In 3D tissue, vulnerability may be further altered due to the stability of vortex filaments (53–55) and complex anatomical structures (7,56–58). However, our conclusions from the 1D cable study provide the quantitative basis to guide more detailed analyses of vulnerability to reentry in 2D and 3D tissue.

APPENDIX

Assume S1 is applied at t = 0 and location x = 0 (Fig. 1 A), the time that the waveback of S1 wave propagate to the position x is

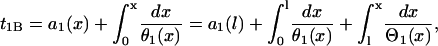(A1)

where a₁(x) is the APD of the S1 wave and Θ₁ is the waveback velocity of the S1 wave. S2 occurs at t = ΔT_S1S2 and location x = l. ΔT_S1S2 is the time interval between the S1 and S2 stimulation. The time that the wavefront of the S2 wave propagates to the same position x is

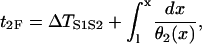(A2)

where θ₂(x) is the wavefront velocity of the S2 wave at location x. Note that Eq. A2 is also applicable to the S2* wave with its CV being negative and the wavefront location x < l. The DI preceding the S2 wave or S2* wave at position x is

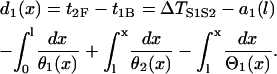(A3)

θ₂ is governed by Eq. 3, i.e., 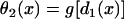. Θ₁ is governed by Eq. 5, i.e., 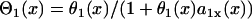. Equation A3 is equivalent to the following differential equation for d₁(x) with respect to x:

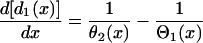(A4)

with the initial condition

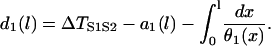(A5)

Equation A4 is the kinematics equation (Eq. 8 in the text) that we used to derive the vulnerable window either analytically or numerically.

If one defines the waveback as the refractory front, then Eq. A3 becomes

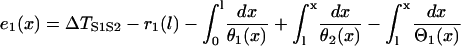(A6)

with

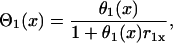(A7)

where r₁(0) is the refractory period of the S1 wave at location x = 0, with its relation to APD (Fig. 1 C) as 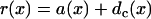. e₁(x) is the temporal excitable gap in front of the S2 wave, which is defined as 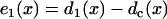. r_1x is the spatial gradient of the refractory period of the S1 wave. Equation A6 is equivalent to the differential equation

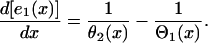(A8)

In general, Eq. A4 cannot be solved analytically due to the nonlinearity. It can be solved when the spatial distribution of APD is a piecewise linear function (Fig. 3 A):

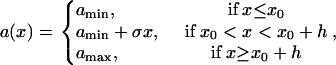(A9)

where 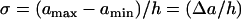is the APD gradient. We also assume that the S1 wave propagates at its maximum velocity θ₀ so that its waveback velocity is

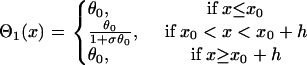(A10)

Inserting 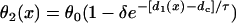(Eq. 4) into Eq. A4, and the solution of Eq. A4 is

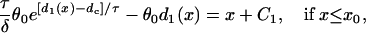(A11a)

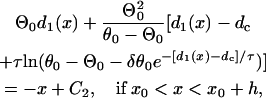(A11b)

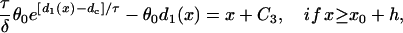(A11c)

where C₁, C₂, and C₃ are integration constants and 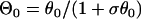. Assume S2 is applied at x = l, then C₁ can be determined by the initial condition d₁(l) = ΔT_S1S2 − a₁(l) − l/θ₀ from Eq. A5. C₂ is then determined by d₁(x₀), which is obtained from Eq. A11a, and C₃ is determined by d₁(x₀ + h), which is obtained form Eq. A11b.

For the S2 wave to successfully propagate through the gradient region, the DI before the S2 wave at location x₀ + h has to be greater than the critical DI, i.e., 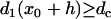, or the S1S2 interval is greater than a critical interval 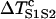. In other words, at this critical condition we have

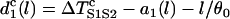(A12)

and

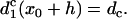(A13)

The vulnerable window w for S2 applied at location l is then defined as (see also Fig. 1 C)

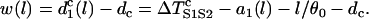(A14)

In principle, by inserting Eqs. A12 and A13 into Eq. A11, one can obtain w(l). Since an explicit solution for d₁(x) from Eq. A11a cannot be obtained, Eq. A11b cannot be solved to obtain w(l). However, we can obtain w(l) using certain approximations. Assuming that S2 is applied at l < x₀ and 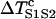is large so that the wavefront velocity of S2 is ∼θ₀, and since Θ₁ = θ₀, the DI will be almost unchanged unless x > x₀. In this case, one can approximate the DI at x₀ by 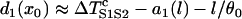, which is the same as Eq. A12. If S2 is applied at l > x₀, Eq. A12 still holds. Therefore, inserting Eqs. A12 and A13 into Eq. A11b, we obtain

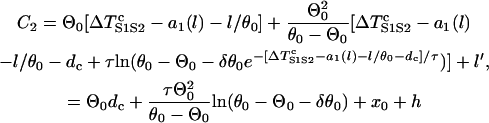(A15)

where

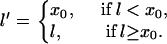(A16)

Again assuming that 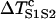is large so that 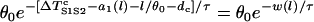can be neglected in Eq. A15, one obtains the vulnerable window by using Eqs. A14 and A15 as

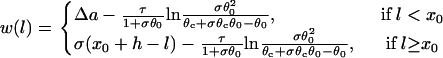(A17)

Equation A17 shows that if S2 occurs in the short APD region (l < x₀), w is independent of where S2 is applied, whereas if S2 occurs in the APD gradient region (l > x₀), w depends linearly on the S2 location, as shown in Fig. 4. However, as l becomes closer to x₀ + h, w becomes smaller, and the term 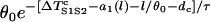will become bigger so that it can no longer be neglected in Eq. A15, and thus Eq. A17 will become less accurate and invalid. For example, when l = x₀ + h, w becomes negative in Eq. A17, which is incorrect.

If APD gradient is descending (Fig. 3 B), i.e.,

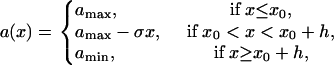(A18)

then conduction block occurs for the wave that propagates opposite to the S1 wave (e.g., the S2* wave in Fig. 1 A) when APD gradient is greater than the critical gradient. In this case, the waveback velocity of the S1 wave is

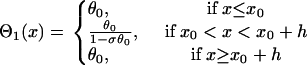(A19)

and the solution of Eq. A4 is

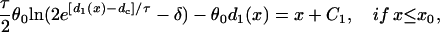(A20a)

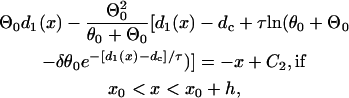(A20b)

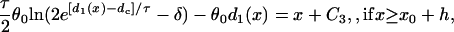(A20c)

where C₁, C₂, and C₃ are integration constants and 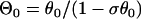. Again, w(l) cannot be explicitly solved from Eq. 20. For conditions in which w(l) is large, it can be obtained similarly as in the ascending case. If S2 is applied at l > x₀ + h, one can use Eq. A20c and the approximation of 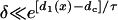to obtain 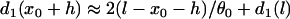with d₁(l) = ΔT_S1S2 − a₁(l) − l/θ₀. Similar to the ascending case, we obtain the vulnerable window by using Eqs. A14 and A20b with the critical conditions Eq. A12 and 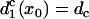as:

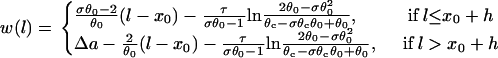(A21)

In this case, w depends on the S2 location l whether S2 is given in short or the sloping region of APD, differing from the ascending case. Again, for small w, the term 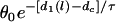will become bigger so that it can no longer be neglected in the derivation of Eq. A21, and it will become less accurate and invalid.