Tryptophan Rotamers as Evidenced by X-Ray, Fluorescence Lifetimes, and Molecular Dynamics Modeling

Abstract

We investigated the native-state dynamics of the Bacillus caldolyticus cold-shock protein mutant Bc-Csp L66E, using fluorescence and appropriate molecular dynamics methods. Two fluorescence lifetimes were found, the amplitudes of which agree very well with tryptophan rotamer populations, obtained from parallel tempering calculations. Rotamer lifetimes were predicted by transition-state theory from high-temperature simulations. Transition pathways were extracted from the transition rates between individual rotameric states. The molecular dynamics also reveal the loop fluctuations in the native state.

INTRODUCTION

Side-chain rotamers located at the protein surface play a key role in various biological processes, including protein-ligand binding (1), protein-protein recognition (2), protein-DNA binding (3), protein folding (4,5), and stability (6). If we want to fully understand (and ultimately predict) all those processes, we need to know the different rotamer populations, their stability, and the important factors that contribute to their equilibrium distribution.

Rotamers may also be used as probes for protein dynamics. Tryptophan fluorescence spectra, quantum yields, and lifetimes depend highly on the surrounding electric field (7–10). The main fluorescence quenching mechanism is believed to be electron transfer (11). Relating tryptophan fluorescence lifetimes to the local environment is complicated by the multi-exponential decay observed in most proteins. In recent years, much experimental and theoretical work has been published that suggests the existence of rotameric states as the source of this multi-exponential decay (12–17). Other proposed mechanisms include reversible electron transfer of the excited tryptophan (18), spectral relaxation of the excited state (19), and energy transfer to different acceptors (20). Until now, no exclusive evidence has been given for the rotamer model or for any other model.

Here, we investigate the basic conditions for the rotamer model using computational methods. If rotamers are the cause of multiple fluorescence lifetimes, these rotamers should be sufficiently populated and have rotamer lifetimes exceeding the corresponding fluorescence lifetimes. As a first indication for the existence of rotamers, we considered a small protein of which the x-ray structure suggests two equally populated Trp conformations: the Bacillus caldolyticus cold-shock protein mutant Bc-Csp L66E with Protein Data Bank (PDB) code 1HZB (21).

Cold-shock proteins (CSPs) represent a widespread family of small proteins that contain the conserved nucleic-acid-binding cold-shock domain (CSD). The CSD harbors the nucleic-acid-binding motifs RNP-1 and RNP-2. Many CSPs are expressed after a cold shock (22). Bc-Csp is a 66-residue β-barrel consisting of five antiparallel β-strands. This thermostable protein has been extensively studied for its folding kinetics and its stability in relation to its homolog Bs-CspB from the mesophylic Bacillus subtilis (23–26). The x-ray structure of 1HZB resembles strongly the conformation of its wild-type counterpart (PDB code 1C9O). The stability of 1HZB is situated between Bs-CspB and Bc-Csp.

To study these dynamical aspects, parallel tempering (PT), or replica-exchange molecular dynamics, allow us to obtain a statistical distribution of the protein conformational space in a very efficient and rigorous way (27,28). The method has been used for studying folding of proteins containing up to 46 residues in explicit solvent (29). For larger proteins, however, simulation times become prohibitively long. By limiting the search space to the native state and by including volume exchanges as well as temperature exchanges, we were able to explore the local dynamics in great detail.

MATERIALS AND METHODS

Materials

Bc-Csp was purified as described by Mueller et al. (30) and donated by Prof. Dr. F. X. Schmid. Acrylamide and N-acetyltryptophanamide were purchased from Sigma Chemical (St. Louis, MO). All other chemicals were analytical grade. Distilled and deionized water (ddH₂O) was used throughout the experiments. The buffer solution used for the fluorescence measurements contained 25 mM Tris, pH 8.2, 2.5 mM CaCl₂, and 50 mM NaCl. All solutions were filtered through a 0.22-μm filter (Millipore, Bedford, MA) and were spectroscopically pure.

Time-resolved fluorescence decay

Fluorescence lifetimes were measured using automatic multi-frequency phase fluorometry between 1.6 MHz and 1 GHz as described previously (12). N-acetyltryptophanamide in ddH₂O with a fluorescence lifetime of 3.059 ns (at 22°C) was used as reference. Data analysis was performed using a nonlinear least-squares algorithm (31). Measurements performed at different emission wavelengths (330–380 nm, 10-nm intervals) were analyzed simultaneously with global analysis (Globals Unlimited) to improve the recovery of lifetimes and amplitude fractions (32). The data were fitted using the modified Levenberg-Marquardt algorithm, assuming that the fluorescence lifetimes are independent of the wavelength (33). Quantum yields, radiative rate constant, and wavelength-independent amplitude fractions were determined as described by Hellings et al. (17).

Fluorescence quenching

The quenching of Trp⁸ in Bc-Csp wild-type (10 μM) with increasing amounts of quencher was performed by adding aliquots of a freshly prepared 1-M acrylamide stock solution to the cuvette, after which the changes in the fluorescence lifetimes τ_i and corresponding amplitude fractions α_i were monitored. The dependency of the reciprocal fluorescence lifetime on the quencher concentration was fitted by the classical Stern-Volmer equation (34) and used to calculate the quenching constant k_q.

Dead-end elimination method

The dead-end elimination (DEE) method (35) was used to determine the possible Trp conformations in Bc-Csp 1HZB. Briefly, the method uses an extensive rotamer library and combines possible rotamers to find the global minimum energy conformation (GMEC) for a given backbone structure. A smart elimination of rotamers that cannot be part of the GMEC avoids the combinatorial explosion and makes the calculation of the GMEC possible. The identification of the rotamer clusters occurred as previously described by Hellings et al. (17). A full-hydrogen model and energy-minimized x-ray structure (PDB code 1HZB) was used as the starting structure. The used rotamer library was an enhanced version of the library of De Maeyer et al. (36). The DEE algorithm has been implemented in the BRUGEL package (37) using the CHARMM force field (38).

Molecular-dynamics simulations

All molecular-dynamics (MD) simulations were performed using the Amber 2003 force field (39) with a modified version of the Amber 8 software (40). The smooth Particle-mesh Ewald method (41) was employed to accommodate long-range electrostatic forces. The nonbonded cut-off for van der Waals interactions was set to 9 Å. Covalent bonds involving hydrogen atoms were constrained using SHAKE (42). A time step of 1 fs was used. Samples were collected every 0.1 ps. The temperature was controlled using the weak-coupling algorithm (43). The initial structure was obtained from monomer A of the x-ray structure of Bc-Csp 1HZB (Trp⁸ χ1 = 70°, χ2 = −97°). Three sodium ions were added in a shell around the protein using a Coulombic potential on a grid. The neutralized protein was solvated in a truncated octahedral box containing 3190 TIP3P (44) water molecules. Minimization was carried out in three stages. First, the solvent was relaxed for 10,000 steps, keeping the solute restrained. Next, the protein was relaxed for 10,000 steps with restraints on the solvent. In the third stage, both solute and solvent were relaxed for 15,000 steps with no restraints. The backbone root mean-square deviation (bRMSD) between the relaxed protein and the x-ray structure was 0.62 Å. To improve sampling of the native state, the protein was allowed to move freely below 2.5 Å bRMSD from the relaxed x-ray structure. Above this threshold, the system was penalized by a harmonic restraint on the bRMSD with a force constant of 10 kcal mol⁻¹ Å⁻². Solvent-accessible surface areas (SASA) were calculated using the program NACCESS (45), which is an implementation of the Lee and Richards method (46). Secondary structures were assigned with the program DSSPcont (47), which is a continuous version of the discrete classification used by the DSSP (48) program. Contacts are defined as occurring whenever the C_α atoms of two nonneighboring amino acids are within 6.5 Å of each other. The fraction of native contacts (Q) is taken as the fraction of contacts found in the relaxed x-ray structure, which contains 134 contacts.

Parallel tempering

The PT simulation was carried out based on the method of Paschek and García (49). Trial swaps were performed between replicas with different temperatures and volumes. The acceptance probability for replica exchange between two states i and j with corresponding temperatures T_i and T_j and box volumes V_i and V_j is given by

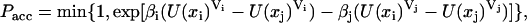(1)

with β = 1/kT and U(x)^V being the potential energy of the state with coordinates x and volume V. The energy U(x_i)^Vj is approximated as

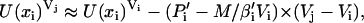(2)

where M represents the number of molecules in the simulation box. P_i′ and β_i′ denote the instantaneous pressure and temperature. An analogous expression is used for U(x_j)^Vi.

It was observed that, for efficient sampling of the Trp⁸ χ2 dihedral angle space, decreased densities and high temperatures were necessary since when the system was heated without decreasing the density, χ2 transitions became very unlikely due to the high system pressure. Therefore, 32 replicas were distributed exponentially over a 300–645 K temperature range and evenly over a 1.02–0.65 g cm⁻³ density range. Temperature and volume exchange moves occurred simultaneously. Volume changes were performed such that only intermolecular distances were altered. It is important to note that sudden volume changes can cause considerable nonequilibrium effects, even if those volume changes are small. This was evidenced by jumps in the potential energy plots (data not shown). To alleviate this behavior, densities were allowed to change gradually over a time period of 0.25 ps, followed by a 0.25-ps equilibration time before data collection.

For the generation of starting conformations, each replica was heated to its target temperature, changed gradually to its desired density, and subsequently simulated for 0.5 ns without replica-exchange moves. Replicas were simulated in the NVT ensemble. The time constant for temperature coupling was 0.5 ps. Exchanges were attempted every 0.5 ps. Acceptance probabilities varied between 0.08 and 0.20. The PT simulation was carried out for 16.2 ns per replica, from which the last 11.8 ns were used to calculate the reported thermodynamic properties. Standard errors of the thermodynamic averages were calculated using the statistical inefficiency method (50).

High-temperature MD

Constant pressure simulations (1 bar) were carried out for eight runs at five different temperatures: 425 K, 450 K, 475 K, 500 K, and 525 K. Starting coordinates and velocities were collected form 1-ns simulations at temperatures ranging between 500 K and 600 K. The structures were equilibrated for another nanosecond. The first transition of every run was discarded. Simulation times ranged between 12 ns for the highest- and 22.8 ns for the lowest-temperature run, with an aggregate simulation time of 560 ns.

The total transition rate constant k_tot,i (T), defined as the sum of all rate constants k_j,i (T) originating from rotamer i at temperature T (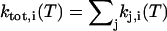), was calculated by numerical integration (51)

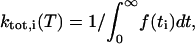(3)

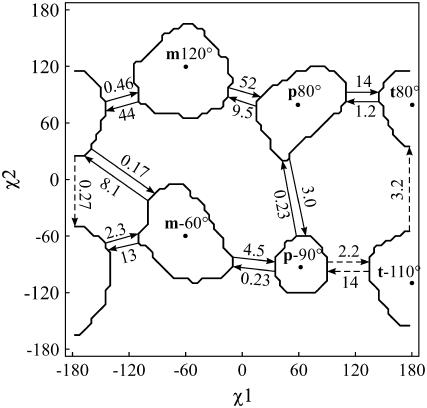
where f(t_i) is the fraction of residence times longer than t_i within the boundaries of rotamer i. The boundary of a rotamer was taken as the contour line in χ1 × χ2 space that contains 95% of its population (see Fig. 5). When the side-chain torsion angles were outside any rotamer boundary, it was assigned as its last visited rotamer state. Using the high-temperature rate constants, we extrapolated kinetic data at room temperature from transition state theory by construction of Eyring plots (see Fig. 4). Individual rate constants k_j,i from rotamer i to j were computed as

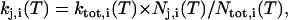(4)

where N_j,i is the number of transitions from i to j and N_tot,i is the total number of transitions originating form i. From the individual transition rate constants, the relative equilibrium concentrations C_i were computed by solving the set of six homogeneous linear equations

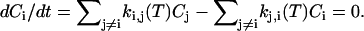(5)

FIGURE 5.

χ1 × χ2 map of the six stable rotamers and a schematic representation of the observed transitions at 500 K, with transition rates given in ns⁻¹. The dashed arrows indicate the reaction path between p−90° and t80°. The contour lines enclose 95% of the population of each rotamer.

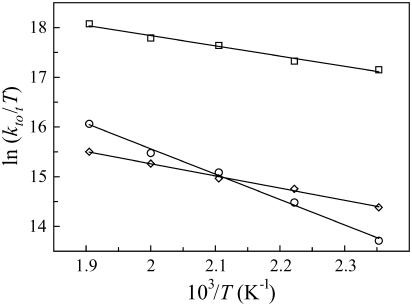
FIGURE 4.

Eyring plots from the high-temperature dynamics for the three most stable rotamers, based on the total transition rate constants k_tot,i (T). p−90° (○), t80° (⋄), and p80° (□).

Rotamer transition pathways were determined on the basis of mean first passage times (MFPT) for discrete kinetics (52). The MFPT τ_bi from state i to b is given by

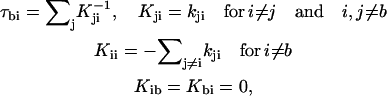(6)

where 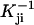is the inverse matrix of the matrix K_ji and k_ji is the individual transition rate from rotamer i to j. The transition path from rotamer state a to b is defined as the path for which each intermediate step from state i to j maximizes 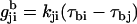. For the first step, i = a, and for the last step, j = b.

Nomenclature

Rotamer nomenclature was taken from Lovell et al. (53). Thus, for Trp χ1, we used t, m, and p, representing trans, minus 60°, and plus 60°, respectively. Trp χ2 values were rounded to the nearest 5°.

RESULTS AND DISCUSSION

Fluorescence lifetimes

The fluorescence decay of Trp⁸ in Bc-Csp was measured at emission wavelengths ranging from 330 to 380 nm in 10-nm intervals. The decay curves were analyzed by single-curve analysis of the data at each wavelength and global analysis of data for seven emission wavelengths. The lowest χ² value, defined as the correctness of fit, was obtained with a double exponential fit, yielding lifetime components τ₁ = 2.45 ns and τ₂ = 6.16 ns with respective amplitude fractions α₁ = 0.29 and α₂ = 0.71 (Table 1).

TABLE 1.

Trp⁸ fluorescence lifetimes and amplitude fractions in Bc-Csp

α1	τ1 (ns)	α2	τ2 (ns)	χ2*	Acrylamide† (M)
0.29 ± 0.06	2.45 ± 0.03	0.71 ± 0.06	6.16 ± 0.14	1.36	0.00
0.27 ± 0.04	1.86 ± 0.05	0.73 ± 0.05	3.94 ± 0.10	1.22	0.05
0.28 ± 0.06	1.52 ± 0.09	0.72 ± 0.07	2.96 ± 0.12	1.30	0.10
0.25 ± 0.09	1.12 ± 0.10	0.75 ± 0.08	1.85 ± 0.09	1.59	0.20
0.27 ± 0.08	0.84 ± 0.11	0.73 ± 0.07	1.39 ± 0.15	1.61	0.30
0.26 ± 0.05	0.65 ± 0.08	0.74 ± 0.05	1.15 ± 0.11	1.45	0.40

^*The value that defines the correctness of the fit.

^†Quenching of Trp⁸ in Bc-Csp (10 μM) with increasing amounts of acrylamide.

Fluorescence quenching with acrylamide

To investigate the solvent accessibility of the two lifetime components, an acrylamide quenching study was performed. The measurements were done at 350 nm. The results are shown in Table 1. Both reciprocal lifetimes show a linear dependency on the acrylamide concentration. The bimolecular quenching constants k_q1 and k_q2 are 2.63 ± 0.12 M⁻¹ ns⁻¹ and 1.80 ± 0.09 M⁻¹ ns⁻¹ for τ₁ and τ₂, respectively, indicating that the shortest lifetime components correspond to the most solvent accessible rotameric state.

Native-state dynamics

We used the parallel tempering scheme for studying the dynamics of the folded protein. To improve sampling of the native state, the protein was allowed to move freely below 2.5 Å bRMSD from the relaxed x-ray structure. Above this threshold, the system was penalized by a harmonic restraint on the bRMSD. This approximation is valid if three conditions are met. First, the native state should be the dominant state at room temperature (this is true for most proteins). Second, rotamer transitions in the native state must occur on timescales much smaller than folding-unfolding transitions, indicating that the rotamer transition does not require unfolded conformations. Third, the native-state basin should be within the imposed threshold of 2.5 Å around the relaxed x-ray structure. For 1HZB, which folds in a two-state N ↔ U reaction, the first condition has been experimentally confirmed, with native- and unfolded-state lifetimes τ_N = 350 ms and τ_U = 1.5 ms (54). The second condition is satisfied for Trp⁸, as will be shown below. For the third condition, we do not know the space occupied by the native state beforehand. However, recent theoretical and experimental studies suggest that protein-folding funnels are very narrow, with estimated maximum backbone variation ranging between 1 Å and 2 Å (55–58).

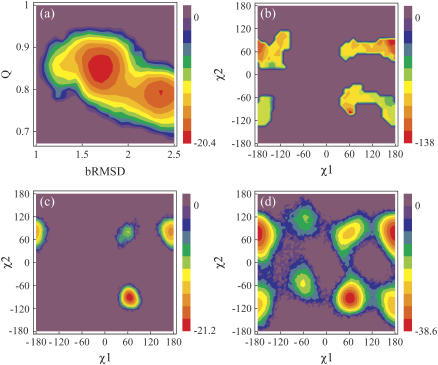
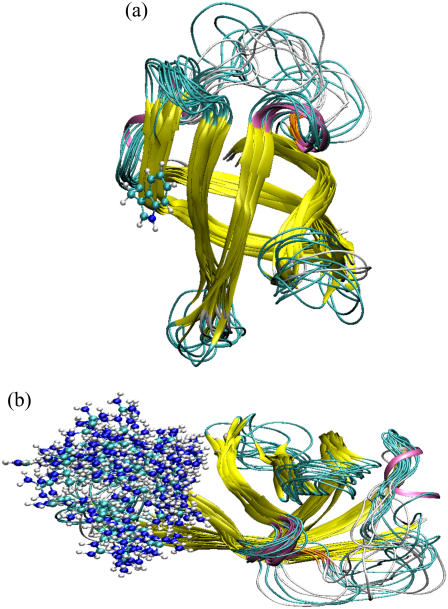
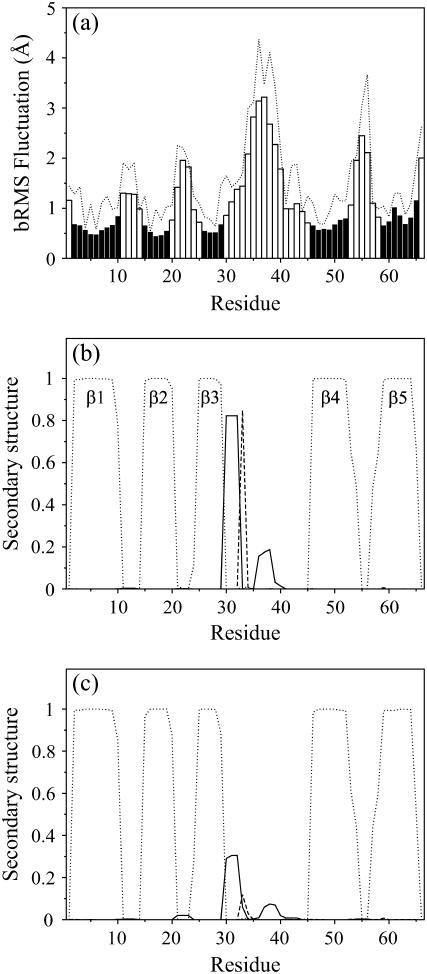
Fig. 1 a represents the free energy as a function of bRMSD and the fraction of native contacts (Q). Within the confined space of 2.5 Å, the native state bRMSD ranges over 1.5 Å. Two free-energy wells, with minima at 1.7 Å and 2.35 Å bRMSD, are connected by a small low-energy pathway and have relative populations of 0.69 and 0.31, respectively. The observed bRMSD values from the relaxed x-ray structure are attributed mainly to the loops, as the β-sheet bRMSD stays below 1 Å and is nearly independent of the total bRMSD (data not shown). The loop fluctuations are also evident from Figs. 2 and 3 a, and agree well with ¹⁵N relaxation data on Bs-CspB (59). As expected, the largest fluctuations are found in the longest loop connecting the sheets β3 and β4. Also, loop β4-β5 experiences considerable fluctuation. The total RMS fluctuation of Arg⁵⁶ on the loop between β4-β5 is remarkably high (Figs. 2 b and 3 a), with the guanidine group reaching out far from the protein core or making close contact with the CSD (β2 and β3). Keeping in mind the strong arginine-nucleic acid binding potential, we suggest that Arg⁵⁶ acts as an antenna for possible nearby nucleic acid strands, and subsequently brings them into contact with the nucleic acid binding domain.

FIGURE 1.

Energy contour maps in units of kJ mol⁻¹. (a) Free energy as a function of Q and bRMSD, from PT. The highest bRMSD well corresponds with a loss of the 3₁₀-helix structure. (b) Potential energy in function of Trp⁸ χ1 and χ2, from DEE. The energies are calculated as the total nonbonded energies E_totnb for all structures with a negative E_totnb. Free energy in function of Trp⁸ χ1 and χ2 from (c) PT and (d) 500 K MD. The relative free energy ΔG between two states i and j with relative populations P_i and P_j is calculated as 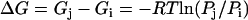, where R denotes the universal gas constant.

FIGURE 2.

Superposition of 15 native-state structures of 1HZB from PT. The structures were carefully chosen to represent the occupied conformational space. The color scheme is as follows: 3₁₀-helix (mauve), extended β-strand (yellow), isolated β-bridge (orange), hydrogen-bonded turn (cyan), and coil (white). To these ribbon models were added in ball-and-stick models the side chains of (a) Trp⁸ in the p−90° state, and (b) 118 Arg⁵⁶ conformations.

FIGURE 3.

(a) bRMS fluctuation (bars) and total RMS fluctuation (dotted line) as a function of the residue number, from PT. The black bars indicate β-sheet residues. (b and c) Secondary-structure content in function of residue number for states belonging to (b) the low-bRMSD free-energy well and (c) the high-bRMSD free-energy well (see Fig. 1 a). Curves represent the 3₁₀-helix (solid lines), isolated β-bridge (dashed lines), and extended β-strand (dotted lines).

A high flexibility does not imply a total lack of structure. In particular, the 3₁₀-helix (Phe³⁰-Thr³¹-Ala³²), which is present in all CSP crystal structures but absent in all NMR solution structures in the PDB to date, makes up a vital part of the molecule and is extrastabilized by a β-bridge between Ile³³ and Val⁶³ (Figs. 2, orange, and 3, b and c). Both structural elements are especially well preserved in the lower, but largely destroyed in the higher, free-energy well (Fig. 3, b and c).

Tryptophan rotamers

The 1HZB crystal structure (21) is dimeric, though Bc-Csp and mutants have been shown to exist as monomers in solution (60). Trp⁸ of monomer B is disordered, containing two distinct conformations with equal occupancies (p−95° and t100°), whereas the Trp⁸ side chain of monomer A occupies only p−95°.

Applying the DEE method, as defined by Hellings et al. (17), on Trp⁸ of Bc-Csp 1HZB identified two rotamer clusters (Fig. 1 b) with energy minima at p−100° and t90°. These two clusters correspond to the two x-ray Trp conformations. However, the energy plot reveals also clusters for the rotamer p70°, as can be expected for a solvent-exposed residue. The PT calculation produced matching rotamers p−90° and t80° (Fig. 1 c), with respective populations 0.71 and 0.27 (Table 2). These values agree remarkably well with the amplitude fractions α₂ (0.71) and α₁ (0.29) of the fluorescence lifetimes τ₂ and τ₁ (Table 1). Furthermore, if we assign p−90° to τ₁ and t80° to τ₂, fluorescence quenching constants k_q1 and k_q2 correlate with average solvent accessibilities (Tables 1 and 2). Comparison with DEE demonstrates the importance of explicit solvent and/or backbone dynamics on the rotamer distribution, despite the small local backbone fluctuation. Nevertheless, DEE was able to identify the two most stable PT rotamers, which demonstrates the usefulness of this computationally inexpensive method as a rough estimation of rotamers.

TABLE 2.

Trp⁸ rotamer thermodynamic and kinetic properties in 1HZB

	p−90°	t80°	p80°
Population*	0.71 ± 0.04	0.27 ± 0.03	0.016 ± 0.007
τrot (ns)†	(52 ± 13) × 101	21 ± 2	0.93 ± 0.17
ΔH°‡ (kJ mol−1)†	42.4 ± 1.7	20.4 ± 0.8	17.1 ± 1.3
−TΔS°‡ (kJ mol−1)†	−5.0 ± 1.1	9.0 ± 0.5	4.5 ± 0.8
ΔG°‡ (kJ mol−1)†	37 ± 2	29.4 ± 0.9	21.6 ± 1.5
SASA (%)*	42.0 ± 0.3	44.4 ± 0.6	55.4 ± 1.2
SASA SD (%)*	3.8	5.6	3.7

τ_rot, rotamer lifetime at 300 K; ΔH°^‡, activation enthalpy; ΔS°^‡, activation entropy; ΔG°^‡, activation free energy; SASA, Trp⁸ solvent-accessible surface area, relative to the tripeptide Ala-Trp-Ala; SD, standard deviation.

^*Calculated as ensemble averages from the PT simulation.

^†Calculated from the high-temperature simulations using transition state theory.

Side-chain kinetics

For the three rotamers observed with PT, we applied transition-state theory to the high-temperature MD simulations to obtain total transition rate constants at room temperature. The Eyring plots (Fig. 4) tell us that p−90° is the most kinetically stable rotamer below 475 K, whereas above 475 K t80° has a higher free energy of activation. This is due to both a higher ΔH°^‡ and a lower ΔS°^‡ for p−90° (Table 2). The extracted τ_rot values for p−90° and t80° are 0.5 μs and 21 ns, respectively (Table 2), which is well above τ₂ (6.16 ns) and τ₁ (2.45 ns) and well below τ_N (350 ms) and τ_U (1.5 ms). These lifetimes clearly reflect the population analysis result of parallel tempering, thus corroborating the use of Eyring plots over an extended temperature range. As expected for a solvent-exposed residue, ΔG°^‡ is highly correlated with SASA values, especially when the SASA standard deviation is taken into account (Table 2).

In principle, Eyring plots can also be constructed to obtain the individual rotamer transition rates at room temperature. From these rates, rotamer populations and reaction paths can be calculated. As shown in Fig. 4, straight curves were obtained for the total transition rates. For the individual transitions, however, prohibitively long simulation times would be required to obtain straight lines. Therefore, we will only report individual rates and reaction paths at a fixed temperature of 500 K.

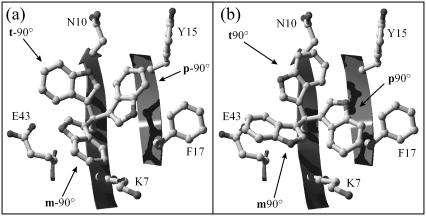
Fig. 5 depicts all observed transitions and rate constants at 500 K on a χ1 × χ2 map (see also Fig. 1 d). It is clear from the graph that χ1 transitions are energetically more favorable than χ2 transitions. This trend is even more pronounced as the temperature decreases. Note also the facile m−60° ↔ t80° transition, which is a combination of χ1 and χ2 transition, and the absent m−60° ↔ m120° transition. For m−60°, a χ2 transition via 0° with χ1 fixed would lead to a steric clash between the Trp⁸ pyrrole ring and the backbone of Lys⁷. When, nevertheless, χ2 is forced to rotate, it must therefore be accompanied by a χ1 rotation, leading to t80°. Furthermore, the minimum-energy χ2 angle for m−60° at 300 K is ≈30° larger than the ideal angle of −90° because of steric interactions with the Lys⁷ side chain (Fig. 6). This χ2 equilibrium shift, accompanied by collisions with the very flexible Lys⁷ side chain might help crossing the χ2 rotational barrier.

FIGURE 6.

Tryptophan rotamers in Bc-Csp 1HZB. Superposition of the six Trp⁸ rotamers in their ideal positions and the surface-exposed residues within a 5-Å radius of Trp⁸. (a) m−90°, p−90°, and t−90°. (b) m90°, p90°, and t90°.

To quantify the mechanism, we computed the transition path at 500 K between the most stable rotamers p−90° and t80°. Both the forward and backward transitions follow the same path via t−110° (Fig. 5), in accordance with the principle of microscopic reversibility. The same pathway is followed at lower temperatures. At 525 K, however, p80° is found as the dominant intermediate state. This suggests that the pathway via p80° is entropically favored, whereas the t−110° route has a lower ΔH°^‡.

CONCLUSIONS

The parallel tempering method, combined with volume exchanges and native-state confinement allowed us to obtain precise rotamer distributions. In addition, a detailed study of local protein dynamics in the native state is made possible. In Bc-Csp 1HZB, two Trp rotameric states occupy a considerable amount of simulation time. This is confirmed by x-ray analysis and is in line with the dead-end elimination analysis. The rotamer distribution corresponds remarkably well with amplitude fractions of two fluorescence lifetimes. Solvent accessibilities correlate with acrylamide fluorescence quenching constants. A kinetic analysis reveals that the thermodynamically most stable rotamers are also the most kinetically stable ones. Both rotamers have sufficient kinetic stability to qualify as candidates for the origin of the biexponential fluorescence decay. The data further reveal that the Trp motions are strongly controlled by solvent exposure. In future work, we hope to apply these techniques to address challenging problems such as to what extent rotamer distributions are ubiquitous for exposed Trp residues and what rotation mechanisms are feasible for buried side chains.