Chemical Potential Derivatives and Preferential Interaction Parameters in Biological Systems from Kirkwood-Buff Theory

Abstract

New expressions for chemical potential derivatives and preferential interaction parameters for ternary mixtures are derived for open, semiopen, and closed ensembles in terms of Kirkwood-Buff integrals, where all three components are present at finite concentrations. This is achieved using a simple approach that avoids the use of the general matrix formulation of Kirkwood-Buff theory. The resulting expressions provide a rigorous foundation for the analysis of experimental and simulation data. Using the results, a simple model is developed and used to investigate the possible effects of finite protein concentrations on the corresponding cosolvent dependent chemical potential and denaturation thermodynamics.

INTRODUCTION

Traditionally, the effects of cosolvents on protein solubility and denaturation equilibria have been studied by a variety of binding models (1–5), although other approaches are also available (6,7). This type of approach typically involves the determination of a number of chemically equivalent binding sites and the corresponding equilibrium constant for the binding or exchange process. However, these models provide only an approximation to reality when the cosolvent binds weakly to the protein surface (8). Alternatively, one can relate the changes in protein chemical potential to changes in the solution composition in the vicinity of the protein (9–11). This can involve changes in the first solvation shell (9), or over many solvation shells away from the protein surface (11). Unfortunately, it is usually difficult to determine changes in the solution composition over distances covering one or more solvation shells using current experimental techniques. The above approaches are limited to infinitely dilute protein solutes and provide three different molecular descriptions of the interaction of cosolvents with proteins and their effects on biomolecular equilibria. Hence, our understanding of protein denaturation at the atomic level remains incomplete and therefore requires further study.

All the approaches can be formulated in terms of preferential interactions (8). Preferential interactions provide a thermodynamic measure of the changes in chemical potentials or solution composition (12). There are many types of preferential interaction parameters depending on the concentration scales used (molality, molarity, or mole fraction) and the particular thermodynamic ensemble in which the derivatives are evaluated (12,13). To the best of our knowledge, Ben-Naim was the first to use Kirkwood-Buff (KB) theory to describe the thermodynamic effect of a cosolvent on biomolecular equilibria (14,15). Since then, applications of KB theory to understand the properties of biomolecular systems have also appeared (16–18). More recently, there has been a renewed interest in expressing chemical potential derivatives and preferential interactions for biological systems in terms of KB integrals (11,19–27). Using KB integrals, one can quantify the changes in solution composition (over many solvation shells) and directly relate these changes to thermodynamic effects on the protein. A major advantage of KB theory is that it requires no approximations and therefore provides a solid foundation from which one can rationalize different cosolvent effects.

It is therefore envisioned that the use of KB theory will lead to an improved understanding of cosolvent effects in biological systems. Recent studies are encouraging. Shimizu and co-workers have used KB theory to determine hydration changes for allosteric transitions and ligand binding, and to clarify the assumptions made in osmotic stress analysis (22,28). Shulgin and Ruckenstein have applied KB theory to quantify the excess or deficiency of water around several proteins in the presence of both osmolytes and protein denaturants. As expected, an increase in hydration was observed for the osmolytes, whereas a decrease in hydration was found for the denaturants (25). Schurr et al. have also expressed preferential interactions in terms of KB integrals and used these expressions to develop some simple models for the interaction of cosolvents with proteins. The results suggest a significant excluded volume effect (24). Our own work has focused on using KB theory to understand preferential interactions (19), providing a rigorous link between the results of computer simulations and the corresponding experimental thermodynamic data (23), the development of a model of cosolvent effects based on KB theory (11), and understanding the density changes observed in equilibrium dialysis experiments in terms of KB integrals (29). More recently, Schellman has compared the results from KB theory to the corresponding expressions obtained from thermodynamic binding models (27). Hence, it is clear there is considerable increasing interest in analyzing cosolvent effects in terms of KB integrals.

Kirkwood-Buff theory provides expressions for the composition dependent chemical potential derivatives for solution mixtures in closed systems (constant N) in terms of particle number fluctuations, or equivalently as integrals over radial distribution functions in open systems (constant μ). The general result for any number of components in a closed system can be formulated in terms of ratios of matrix determinants (15,30,31). The corresponding matrix elements are expressed in terms of the KB integrals between species i and j defined as

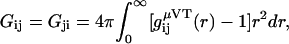(1)

where g_ij(r) is the radial distribution function between species i and j in the open system. Unfortunately, as one moves to ternary or more complex mixtures, the matrix determinants become rather cumbersome to use (14,15,32), even after simplifying the matrices involved (14). Consequently, many studies of ternary solutions, especially those involving biomolecules, have one or more species appearing at infinite dilution in an effort to simplify the algebra required (14,19,23,24,26,33). Even then, it is still difficult to obtain some of the chemical potential derivatives or preferential interaction parameters as they often correspond to semiopen systems and one has to perform additional thermodynamic transformations from the closed system results (15,23–25). Here, a relatively short and simple route to the derivatives for binary and ternary solutions in closed and semiopen systems is demonstrated. The approach generates several new equations valid for finite biomolecule concentrations. One of these equations is then used to investigate the potential effects of the biomolecule concentration on the cosolvent-dependent biomolecule chemical potential in an effort to determine exactly when the infinitely dilute protein approximation is valid. To our knowledge, there have been no previous applications of KB theory to study preferential interactions in ternary systems with finite solvent, cosolvent, and protein concentrations.

KB theory will be used to determine a variety of chemical potential derivatives and preferential interaction parameters in binary and ternary systems. However, the aim is to avoid starting from the KB results for closed systems as they generally involve expressions containing a large number of KB integrals. Instead, we will focus on the primary result obtained from KB theory for fully open systems as given by (15,30)

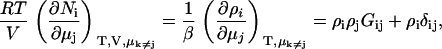(2)

where ρ_i is the number density (molarity) of species i in terms of the average number of N_i molecules in the system, δ_ij is the Kroenecker delta function, and β = (RT)⁻¹. In addition, the Gibbs-Duhem equation for a mixture of n components provides (12),

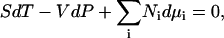(3)

where all the symbols have their usual meanings. The following relationships can be obtained from the above equation,

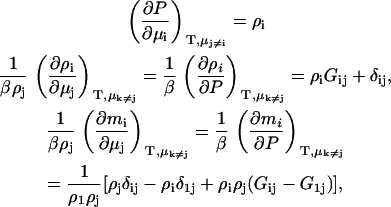(4)

where we have used the fact that the molality is given (to within a constant conversion factor) by m_i = N_i/N₁, assuming that component 1 is the primary solvent. The corresponding pressure changes in an open system are directly related to the osmotic pressure (dP = dΠ). The above information is all that is required to determine the chemical potential derivatives in open, semiopen, or closed systems.

RESULTS

In this section, we will first present results for a binary system to establish the current approach. The corresponding results for ternary systems are then derived by starting from the appropriate expressions in the fully open system and transforming in steps, first to semiopen systems, and then finally to a fully closed system. This provides relatively simple expressions in terms of the KB integrals. Unfortunately, in doing so the relationship to partial molar volumes and activity derivatives, which may be available experimentally, becomes less apparent. The application of KB theory to systems were the common ion effect is important has been outlined previously for the case of an infinitely dilute biomolecule (23). The KB version of the common ion effect in finite biomolecule systems is somewhat involved and will be addressed in a future article. However, the results presented here should be applicable to the majority of protein systems. Several combinations of KB integrals occur repeatedly during the present analysis of both binary and ternary systems. Hence, we will define the following,

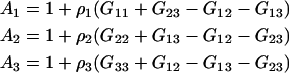(5)

and note that

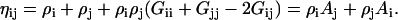(6)

Equation 6 can be used to describe a binary system of 1 and 2 even though A₁ and A₂ contain KB integrals with indices corresponding to a third component—as these KB integrals will cancel in the resulting expressions. It is also apparent that each A_i tends to unity as ρ_i tends to zero.

Open binary system

The results for an open binary system are included here for completeness and for comparison with subsequent expressions. The required derivatives are obtained directly from Eqs. 2 and 4 to give

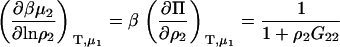(7)

for the molarity derivative and

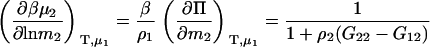(8)

for the molality derivative. The additional KB integral in the molality expression is a direct consequence of the definition of molality and the fact that N₁ is variable.

Closed binary system

One can obtain the required chemical potential derivative in the corresponding closed constant pressure ensemble using an appropriate thermodynamic transformation. It will prove advantageous to start with the inverse of the required derivative in the open system. The appropriate transformation is then,

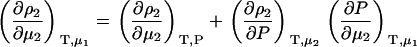(9)

and therefore using Eqs. 2 and 4 one finds

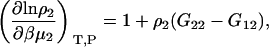(10)

which is necessarily the same result as presented previously (15,30) but involves a simple one-step transformation. The expression for the cross-derivative can be found using Eqs. 3 and 10. The molality scale derivative is provided by the analogous transformation as performed in Eq. 9 to give

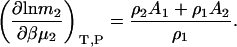(11)

The above approach provides no particular advantage for binary systems as the matrix approach is also easy to solve. However, derivatives for ternary systems are traditionally more problematic and we will see that this type of approach displays distinct advantages.

Open ternary system—constant T, μ₁, μ₃

For biological systems, it is common to define a ternary solution of principle solvent (1), biomolecule (2), and cosolvent (3), and where the system is open to all components except the biomolecule. For this system, the activity derivatives follow directly from Eq. 4. Preferential interactions in ternary systems involve derivatives of the form (∂m₃/∂m₂) and (∂ρ₃/∂ρ₂), where the biomolecule concentration is usually assumed to be low, although we will relax that restriction here. Expressions for these derivatives can be obtained quite easily from Eq. 4 and provide (27)

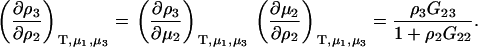(12)

Alternatively, many applications require the use of molality-based derivatives. Here one obtains

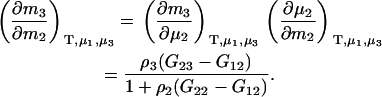(13)

Both of the above expressions are valid for finite biomolecule concentrations and only contain KB integrals involving the biomolecule.

Semiopen ternary system—constant T, P, μ₃

A common ensemble that has been used to interpret preferential interactions in semiopen systems involves a ternary system where the system is open to the cosolvent only (8,13). To obtain the required derivatives, one starts from the fully open system and uses the transformation

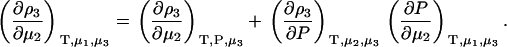(14)

The first term is given by Eq. 2, the third and fourth terms by Eqs. 2 and 4, to give the expression

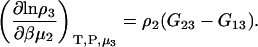(15)

To determine the preferential interaction as defined by 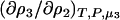one requires

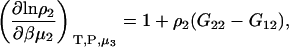(16)

which was obtained from the same approach as used for Eq. 15. Therefore,

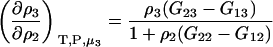(17)

for any biomolecule concentration. The above equation is simpler, can be applied to both finite and infinitely dilute protein conditions, and was obtained with substantially less effort than previous approaches (25). The only disadvantage is it does not express the preferential interaction parameter in terms of activity derivatives and partial molar volumes.

Molality-based derivatives can be determined in the same manner as used previously in Eq. 14. For finite biomolecule concentrations one finds that

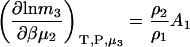(18)

and

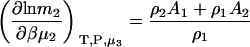(19)

and therefore

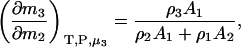(20)

which reduces to the correct expression for an infinitely dilute biomolecule solute (23).

Semiopen ternary system—constant T, P, μ₁

Another common ensemble used for interpreting preferential interactions in biological systems involves a system at constant T, P, and solvent chemical potential. The appropriate expressions for the chemical potential derivatives and preferential interaction parameters for finite biomolecule concentrations are then given by

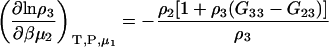(21)

with

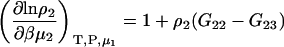(22)

and therefore

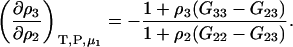(23)

Alternatively, using the molal concentrations, one has

(24)

with

(25)

and therefore

(26)

which again reduces to the correct expression for an infinitely dilute biomolecule solute (23).

Closed ternary system—constant T, P, m₂, or m₃

To generate derivatives in closed systems, a further transformation is required. A change of variables from μ₁ to m₂ and use of the chain rule provides

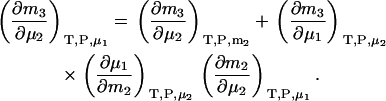(27)

The first term is given by Eq. 24, the third and fourth terms can be obtained in a similar manner as for Eqs. 18, 19, 24, and 25, whereas the fifth term is given by Eq. 25. The same process can be repeated to obtain all three possible derivatives. The final expressions are given by

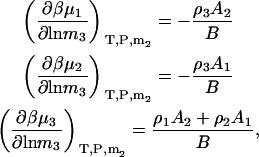(28)

where

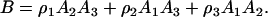(29)

Using Eqs. 5 and 6, one can show that the above equations reduce to the appropriate expressions for binary solutions in the limit that ρ₁, ρ₂, or ρ₃ approach zero. They also obey the Gibbs-Duhem equation at constant T and P,

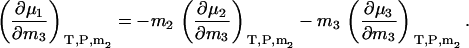(30)

Constant m₃ derivatives in the closed system can be obtained by inspection from Eq. 28, as we have

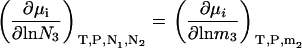(31)

and a simple interchange of indices is possible. This is not always the case for the open or semiopen systems. When derivatives are required using other concentration scales, they can be determined by noting that

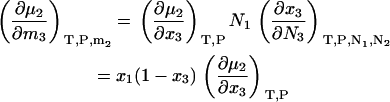(32)

and

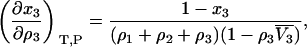(33)

where 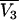is the partial molar volume of the cosolvent. Hence, one finds that

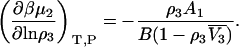(34)

The latter conversion introduces a partial molar volume, which, in principle, could also be expressed in terms of KB integrals. Even so, it is clear that the above equations demonstrate a considerable degree of contraction from the corresponding initial expression that would be provided by the matrix approach.

The above derivatives in closed systems still result in some lengthy expressions. The expressions are simplified considerably if one is only interested in the change in biomolecule chemical potential with cosolvent or solvent activity (a_i). In this case one obtains

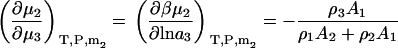(35)

and,

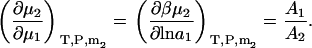(36)

The two above expressions satisfy the known relationships between the different derivatives (13).

Closed ternary system—constant T, P, ρ₂

Finally, the derivative most appropriate for the analysis of the denaturation equilibrium in closed systems using statistical mechanics involves the pseudochemical potential, μ* (15,23). This is related to the total chemical potential according to 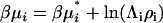, where Λ_i is the thermal de Broglie wavelength (15). The pseudochemical potential isolates interactions between a single fixed solute and any other solution species, including any other solute molecules when the solute is present at finite concentrations. It is equivalent to the change in Gibbs energy on transferring the solute from a fixed position in the gas phase to a fixed position in the solution, including changes to the internal partition function. Noting that 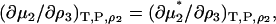one can transform Eq. 15 to give

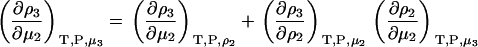(37)

or

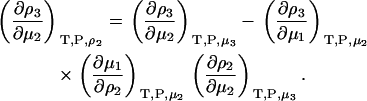(38)

The derivatives at constant μ₂ can be obtained as before and are given by

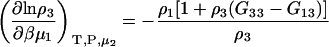(39)

and

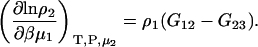(40)

Hence, the final result for the closed system is given by

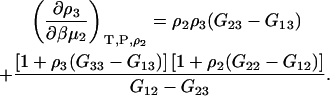(41)

Defining

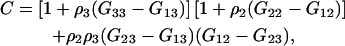(42)

the above derivative can be written

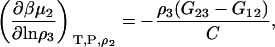(43)

which reduces to the well-known expression for an infinitely dilute biomolecule (19,23)

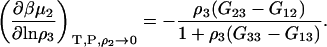(44)

A similar route provides

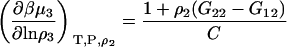(45)

and use of the Gibbs-Duhem equation gives

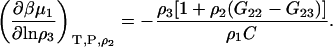(46)

Combining Eqs. 43 and 45 results in the expression

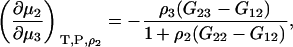(47)

which is different from the result at constant m₂ as given by Eq. 35 even for infinite dilution of component 2. The difference between the two expressions at infinite dilution of 2 is given by

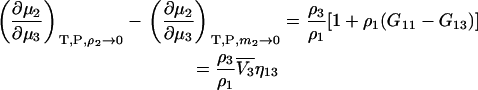(48)

and arises from the volume constraint in the first derivative. This concludes our analysis of ternary systems.

DISCUSSION

In our opinion, the above approach provides a fast and simple route to new and existing expressions for chemical potential derivatives and preferential interactions in a variety of ensembles. Although it is not as general as the matrix formulation of KB theory, it does offer some distinct advantages. First, we have started with expressions in fully open systems and performed stepwise transformations to a semiopen or closed system. Consequently, the algebraic manipulations are easier than if one started from the corresponding result for a closed system and transformed to a semiopen system; primarily because the expressions for fully closed systems are generally the most complicated in terms of KB integrals (14). Second, it is advantageous to work in terms of (∂ρ_i/∂μ_j) rather than (∂μ_j/∂ρ_i) as this considerably simplifies the combination of terms. Third, information concerning the derivatives in several semiopen ensembles is also provided. For instance, it is clear that the expressions for the chemical potential derivatives presented in Eqs. 16, 21, and 39 are the same as for the equivalent closed binary systems where species 3, 1, and 2 are absent, respectively, although the values of the KB integrals will be different due to the presence of a third species. This is also apparent from the Gibbs-Duhem equation.

Using the result presented in Eq. 43, one can investigate the possible effects of finite protein concentrations on the change in biomolecule chemical potential, or protein solubility, observed due to the addition of a cosolvent. In general, the required KB integrals are unknown and vary with composition. However, the differences between KB integrals are often relatively insensitive to composition, and are independent of composition for ideal mixtures (34). Using this approximation, one can integrate Eq. 43 with respect to cosolvent concentration to obtain

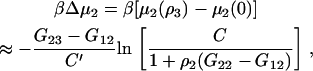(49)

where C′ is the derivative of C with respect to cosolvent concentration (ρ₂ and all ΔG_ij assumed to be constant). Before proceeding, it should be noted that the conditions of constant T, P, and ρ₂ are somewhat unusual from a thermodynamic perspective as they imply that both the pressure and volume remain constant during the addition of a cosolvent molecule. They have been used in previous studies (19,24). Experimentally, this is not possible. However, these conditions are roughly obeyed in many studies as long as the results are obtained from experiments where the protein concentration remains relatively constant for a series of solutions in which the cosolvent concentration is varied. One could also investigate finite protein concentration effects using Eq. 34, but this expression is more difficult to integrate.

To investigate further, some approximate values for the KB integrals are required. A value of G₂₂ = −420,000 cm³/mol has been estimated for the protein chymotrypsinogen, which has a molecular mass of 26 kDa (18). Other values can be estimated from the molar volumes of each species. Using water as the primary solvent (V₁ = 18 cm³/mol) and considering an osmolyte that is larger than the solvent (V₃ = 3V₁) and therefore excluded from the surface, together with the symmetric ideal solution approximation (15), provides values of G₁₁ = −V₁ = −18, G₃₃ = −V₃ = −54, and G₁₃ = ½(G₁₁ + G₃₃) = −36 cm³/mol. This assumes that the activity of the water and cosolvent are not significantly affected by the presence of the protein (25). When the excluded volume dominates the cosolvent effect, the values of G₂₃ and G₁₂ can be estimated from the surface area of the protein (A = 47 nm²) (35), which is taken as equal to that of a sphere with a similar volume (30 nm³) to the protein. The values of G_2j are then given by −A r_j and therefore, using radii of r₁ = 0.15 and r₃ = 0.22 nm, one obtains values of G₁₂ = −4300 and G₂₃ = −6200 cm³/mol. These values and Eq. 49 provide a reasonable description of the effects of both the protein and cosolvent concentrations on the chemical potential of the protein solute.

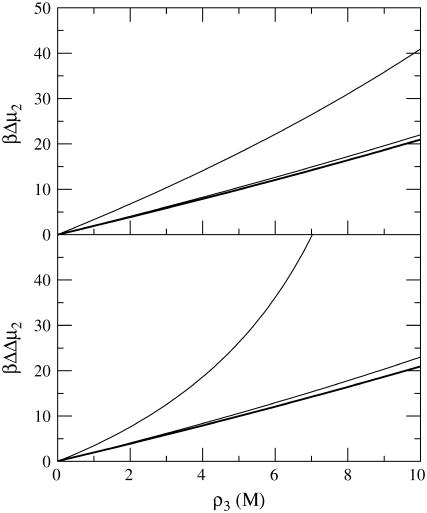
The results are shown in Fig. 1 and indicate an almost linear dependence of the protein chemical potential (βΔμ₂) on cosolvent molarity for low protein concentrations. The effect of additional protein was to increase the effect of the cosolvent with increasing nonlinearity appearing at larger protein concentrations. This is primarily due to the increasingly negative contribution from the protein KB integrals (G_2j) to the value of C′, although the overall value remains positive. However, the effect only appeared for protein concentrations >0.1 mM (0.002 volume fraction, or 3 mg/ml, or ρ₂G₂₂ = −0.042), which is typically much higher than that used experimentally in denaturation studies. Alternatively, when the sign of the values of G₂₃ and G₁₂ are reversed, one obtains a model for a cosolvent that preferentially binds to the protein. In this case, the results are nearly identical to those displayed in Fig. 1, but opposite in sign (data not shown). Hence, within the approximations outlined here, the calculations suggest that the effect of a finite protein concentration can be neglected in most practical situations. However, this may not be true if the protein has a high propensity for aggregation, which can significantly alter the value of G₂₂.

FIGURE 1.

Predicted change in the chemical potential of chymotrypsinogen as a function of molar cosolvent concentration for the native protein (top), and for the difference between denatured and native protein (bottom) according to Eq. 49. The lines correspond to protein concentrations of 0 (thick line), 0.1 mM, and 1 mM, respectively.

Equation 49 can also be used to investigate the effects of finite protein concentrations of the cosolvent dependent protein denaturation (N → D) thermodynamics. However, additional approximations have to be used. In principle, the system now contains four components and so the derivatives should involve KB integrals between both protein conformations (14). This situation will not be treated here as it is rather involved. Instead, we will assume that chemical potential changes for the N and D forms can be treated independently, which should be true under conditions where G_NN = G_DD = G_DN = G₂₂ is approximately satisfied. In this case, the larger exclusion from the denatured state leads to protein stabilization, as displayed in Fig. 1. The same pattern as before was also observed for differences between the chemical potentials of a denatured and native protein (βΔΔμ₂), where a twofold increase in the surface area for the denatured state (G₂₂ remains unchanged) was assumed. Here, the effect of the finite protein concentration did not cancel between the two forms. In fact, the magnitude of the protein effect was slightly larger in this case.

The previous results have focused on chemical potential derivatives and preferential interaction parameters. KB theory also provides expressions for partial molar volumes and the isothermal compressibility in solution mixtures. One can also derive expressions for the partial molar volumes (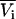) and isothermal compressibility (κ_T) using the same type of approach as outlined above. The partial molar volume of species 2 in a two-component mixture can be obtained from the transformation of 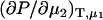to 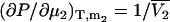and subsequent manipulation. However, when applied to ternary systems, this approach produces a series of equations that do not provide any obvious advantage over the standard matrix formulation. A general expression for the compressibility in terms of partial molar volumes and KB integrals can be obtained in a simple manner from the differential of the volume as a function of T, P, and composition. Consequently, for an n component system one can write

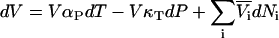(50)

from which one finds that for any j,

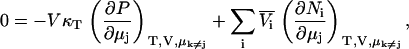(51)

and therefore using Eqs. 2 and 4 a series of expressions are obtained,

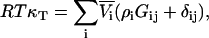(52)

where j = 1,2,3…n. This provides proof of the equation recently postulated by Chitra and Smith (36), but originally derived by Hall using a different approach (37). Furthermore, in the limit of infinite dilution of component 2 in a three-component system, the above equation for j = 2 gives

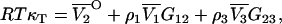(53)

which has been obtained by a shorter route than previous attempts and avoids the evaluation of any matrix determinants (24,38).

CONCLUSIONS

By starting from the KB results for fully open systems, one can generate, in a simple and clear manner, new expressions for chemical potential derivatives and preferential interactions in semiopen and closed ternary systems where all components are present at finite concentrations. The expressions can be used to analyze both experimental and simulated data concerning the interactions of molecules in solution, as quantified by the KB integrals. All the expressions are exact and reduce to the existing expressions derived by assuming infinitely dilute biomolecule concentrations. The approach results in a significant reduction in the algebraic manipulations typically performed in other studies. A new expression has been generated for the derivative of the protein chemical potential in a protein, cosolvent, and solvent mixture as a function of both protein and cosolvent concentrations. A simple model developed using this equation suggests that the effects of finite protein concentrations on the cosolvent-dependent equilibrium at the level used in most experiments is negligible.

The final expressions provide exact relationships between molecular distributions and the corresponding solution thermodynamics. As there are no approximations in KB theory, an analysis of both experimental and simulation data using KB integrals provides a solid foundation for investigating the effects of cosolvents on biomolecules. One requires five KB integrals to fully characterize a ternary system when the protein is at infinite dilution. The values of G₁₁, G₃₃, and G₁₃ are properties of the cosolvent solution in the absence of protein and are typically already known (36). The two remaining integrals (G₂₃ and G₂₁) can be obtained from the experimental data as outlined previously (23,39). For finite protein concentration, the values of G₁₁, G₃₃, and G₁₃ will probably remain unchanged as the protein concentration is usually rather low. However, the G₂₂ integral is then required. This can be obtained from osmotic pressure measurements (15), as indicated by Eq. 4. Therefore, in our opinion, the use of KB theory also presents an approach for the systematic study of protein-protein interactions as described by the value of G₂₂.