Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2006 Apr 14;91(3):873–881. doi: 10.1529/biophysj.106.082115

Translocation of Phospholipids and Dithionite Permeability in Liquid-Ordered and Liquid-Disordered Membranes

Maria João Moreno 1, Luís M B B Estronca 1, Winchil L C Vaz 1
PMCID: PMC1563774  PMID: 16617082

Abstract

We present a detailed study of the translocation rate of two headgroup-labeled phospholipid derivatives, one with two acyl chains, NBD-DMPE, and the other with a single acyl chain, NBD-lysoMPE, in lipid bilayer membranes in the liquid-disordered state (POPC) and in the liquid-ordered states (POPC/cholesterol (Chol), molar ratio 1:1, and sphingomyelin (SpM)/Chol, molar ratio 6:4). The study was performed as a function of temperature and the thermodynamic parameters of the translocation process have been obtained. The most important findings are 1), the translocation of NBD-DMPE is significantly faster than the translocation of NBD-lysoMPE for all bilayer compositions and temperatures tested; and 2), for both phospholipid derivatives, the translocation in POPC bilayers is ∼1 order of magnitude faster than in POPC/Chol (1:1) bilayers and ∼2–3 orders of magnitude faster than in SpM/Chol (6:4) bilayers. The permeability of the lipid bilayers to dithionite has also been measured. In liquid disordered membranes, the permeability rate constant obtained is comparable to the translocation rate constant of NBD-DMPE. However, in liquid-ordered bilayers, the permeability of dithionite is significantly faster then the translocation of NBD-DMPE. The change in enthalpy and entropy associated with the formation of the activated state in the translocation and permeation processes has also been obtained.

INTRODUCTION

The kinetics and thermodynamics of the interaction of amphiphiles with lipid bilayers is of fundamental importance for the understanding of the dynamic properties of biological membranes as well as for the development of new pharmacologically active amphiphilic molecules and modeling of their pharmacokinetics. Additionally, these studies may also elucidate some physical-chemical properties of the bilayers. For the complete characterization of the interaction of amphiphilic molecules with lipid bilayers, the insertion, desorption, and translocation (flip-flop) processes have to be considered. With this aim, we have recently studied the interaction of two fluorescent phospholipids, both labeled with the NBD fluorophore in the headgroup, one of them with two acyl chains (NBD-DMPE) and the other with a single acyl chain (NBD-lysoMPE), with lipid bilayers in the liquid-disordered and liquid-ordered states (1,2). The study of the translocation step was approached using the well-established method of reduction of the NBD group by dithionite (3). In this method, reduction of the NBD group, attached to a lipid embedded in a lipid bilayer vesicle, occurs in two kinetically distinct steps: one is completed within a few minutes and the other extends over several hours or even days. The fast step is the reduction of the NBD chromophore located at the outer surface of the vesicles. Due to the slow permeation of charged molecules (in this case the dithionite anion) across homogeneous lipid bilayers, the slow step was suggested to be essentially due to translocation of the NBD-labeled amphiphile from the inner (inaccessible to dithionite) to the outer (accessible to dithionite) monolayer of the lipid bilayer vesicle (3,4). Several authors have, however, noted that the permeation of the reducing agent could be the process controlling the rate of reduction of the amphiphile in the inner leaflet of the bilayers (3–10). However, there are no quantitative data concerning dithionite permeation of lipid bilayers. In recent published work, we too (1,2) have assumed dithionite permeation to be slow compared to NBD-labeled lipid translocation. In view of the results reported in the work presented here, this assumption was not correct: the slow rate of reduction of the NBD moiety located in the inner monolayer of lipid vesicles must, in fact, be understood in terms of both the translocation of the NBD-labeled lipid and the permeability of dithionite. In the articles from our laboratory cited above, we were studying the complete interaction of the amphiphilic molecules namely insertion/desorption, and the corresponding equilibrium constant, as well as translocation. The latter process was a minor contribution to the articles and was considered only for a matter of completeness; this is the only process that needs correction. In this work, we reassess the translocation process by measuring the translocation of the NBD-derivatives in the absence of dithionite (11). With the knowledge of the translocation rate, as well as the rate of reaction of dithionite with the NBD phospholipids, the permeability of dithionite across the lipid bilayers can now be obtained from the observation of the reduction of NBD in the inner monolayer. In this article, we have developed a kinetic model that accounts for both translocation and dithionite permeation and, therefore, permits calculation of the dithionite permeability rate constants. To our knowledge, this is the first time that this sort of analysis has been performed, and we are able to present true rate constants with predictive value rather than apparent permeabilities (10,12).

The translocation of NBD-DMPE and NBD-lysoMPE, as well as the permeability of dithionite, was studied in large unilamelar vesicles (LUV, 100 nm diameter) prepared from pure POPC and from lipid binary mixtures of POPC/Chol (molar ratio 1:1) and SpM/Chol (molar ratio 6:4). For POPC bilayers, where the bilayer is in a liquid-disordered phase (13), the measurements were done as a function of temperature between 15°C and 55°C, whereas the other two bilayer systems, in the liquid-ordered phases (14,15), were studied between 25°C and 65°C. Using transition state theory, the temperature-dependence of the rate constants enabled us to derive the standard free energy, enthalpy, and entropy changes associated with the formation of the transition state in each process.

MATERIALS AND METHODS

NBD-DMPE (purity >99%) and POPC were from Avanti Polar Lipids (Alabaster, AL); egg yolk SpM was from Sigma-Aldrich Química (Sintra, Portugal); and cholesterol was from Serva/Boehringer Ingelheim (Heidelberg, Germany). All reagents were of the highest commercially available purity. Solvents of analytical reagent grade were from Sigma-Aldrich Química. NBD-lysoMPE was prepared from NBD-DMPE by treatment with phospholipase A2 (2).

Phospholipid concentrations were determined using a modified version of the Bartlett phosphate assay (16) and cholesterol concentrations were determined by the Lieberman-Burchard method as described by Taylor et al. (17). NBD-lysoMPE and NBD-DMPE concentration was determined by spectrophotometry using a molar extinction coefficient at 463 nm of 21000 M−1 cm−1 in methanol. Absorption spectra were recorded on a Unicam UV530 UV/Vis spectrophotometer (Cambridge, UK), and fluorescence measurements were performed on a Cary Eclipse Fluorescence Spectrophotometer (Varian, Victoria, Australia) equipped with a thermostated multi-cell holder accessory. The samples were stirred continuously during measurements. Stopped-flow measurements were performed as previously described (18) on a thermostated stopped-flow fluorimeter (Hi-Tech model SF-61, Salisbury, UK). Data were analyzed using Microsoft Excel and Solver.

Aqueous suspensions of lipids were prepared by evaporating a solution of the desired lipid or premixed lipid mixture, with or without NBD phospholipids, in chloroform/methanol (87:13, v/v) solution by blowing dry nitrogen over the heated (blowing hot air over the external surface of the tube) solution and then leaving the residue in a vacuum dessicator for at least 8 h at 23°C. The solvent-free residue, heated in a water bath at 23°C (POPC samples), at 50°C (POPC/Chol samples) or at 65°C (SpM/Chol samples), was then hydrated with HEPES buffer 10 mM pH = 7.4 with 0.15 M sodium chloride (HEPES buffer), which had been previously heated to the same temperature, and the mixture was left to hydrate for ∼10 min. The amount of hydrating medium added was calculated to result in a final lipid concentration of 4–8 × 10−3 M. The hydrated lipid was subjected to several cycles of vortex/incubation at the specified temperature for at least 1 h to produce a suspension of multilamellar vesicles that was then extruded, using a minimum of 10 passes, through two stacked polycarbonate filters (Nucleopore, Whatman, Springfield Hill, UK) with a pore diameter of 0.1 μm (19). During extrusion, the water-jacketed extruder (Lipex Biomembranes, Vancouver, British Columbia, Canada) was maintained at the temperature used for hydration. For experiments with NBD-DMPE, symmetric LUV were prepared, using the above procedure, with a ratio of 1:3000 NBD-DMPE/lipid, whereas for symmetric LUV with NBD-lysoMPE the ratio was 1:30000.

Asymmetric LUV suspensions were prepared by two different procedures:

  1. LUV with NBD-DMPE, or NBD-lysoMPE, only in the inner monolayer were obtained by adding 1% (v/v) of a solution of sodium dithionite 1 M, in 1 M Trizma base pH 10, to <4 ml of symmetric LUV (4 × 10−3 M for NBD-DMPE or (5–8) × 10−3 M for NBD-lysoMPE), incubation at 23°C for 2 min to allow the reduction of the NBD-DMPE in the outer monolayer, and removal of the dithionite in a Sephadex G75 column eluting with HEPES buffer. The asymmetrically labeled LUV fraction was recovered in the free volume of the column (15–20 ml) while dithionite was eluted in fractions above 40 ml. The asymmetric LUV were diluted with HEPES buffer to the required concentration and stored at 4°C.

  2. LUVs with NBD-lysoMPE only in the outer monolayer were obtained by adding a small volume of the probe in methanol (final methanol concentration ≤0.05%, v/v) to previously prepared LUV of the desired lipid composition. The mixture was left at 23°C for 10 min, with occasional vigorous vortex, and stored at 4°C. The ratio of NBD per lipid in the outer monolayer was 1:25,000, 1:30,000 or 1:40,000 for LUV prepared from pure POPC, POPC/Chol (1:1) or SpM/Chol (6:4), respectively.

To study the kinetics of translocation, 300 μL aliquots of asymmetrically labeled LUV (0.4 × 10−3 M for NBD-DMPE or 3 × 10−3, 4 × 10−3 or 5 × 10−3 M for NBD-lysoMPE in LUV prepared from POPC, POPC/Chol or SpM/Chol, respectively) were transferred to Eppendorf tubes and incubated at the desired temperature. At given times, one or two tubes were stored at 4°C. At the end of the experiment all samples were analyzed, by stopped flow, for their concentration of NBD in the outer and inner monolayer using the reduction of NBD by dithionite (3). For experiments that lasted for more than one day, the samples were usually analyzed at the end of each day.

The permeation of dithionite through the lipid bilayers was studied by adding 1% (v/v) of a solution of sodium dithionite 1 M, in 1 M Trizma base pH 10, to symmetric LUV and following the slow component of the decrease in fluorescence due to reduction of NBD initially present in the inner monolayer. The observed reduction in this case is due to two simultaneously occurring processes: permeation of dithionite into the inner aqueous volume of the LUV and translocation of NBD from the inner to the outer monolayer. The kinetic model taking into account both processes was developed and, knowing independently the translocation rate and the rate of reaction of dithionite with NBD, the permeation of dithionite was obtained. The solutions of dithionite in Trizma base were stored in an ice bath and used within 3 h after preparation.

RESULTS

Reduction of NBD by dithionite

The addition of dithionite, at a final concentration of 0.01 M, pH = 7.4, to symmetrically labeled LUV with NBD-DMPE or NBD-lysoMPE results in a fast decrease in NBD fluorescence to 50 ± 5% of the initial value. This decrease is exponential due to the much larger concentration of dithionite (0.01 M) as compared to NBD concentration (≤2× 10−7 M), with a characteristic time of ∼2 min at 35°C (Table 1). It should be noted that the rate constant for reaction with NBD-LysoMPE is always higher than for reaction with NBD-DMPE in LUV with the same lipid composition and that the rate constant is higher for bilayers prepared from SpM/Chol (6:4). For the interpretation of those rate constants, the reaction of dithionite with NBD-ethanolamine in aqueous solution was also studied and found to be more than two orders of magnitude faster (Table 1). The difference may be interpreted as a consequence of the limited access of dithionite to the crowded headgroup region in the lipid bilayers. In this view, the different rate constants observed for NBD-DMPE and NBD-LysoMPE, and between different lipid compositions, may be indicative of small differences in the position of the NBD group relative to the bilayer surface or different frequencies and/or amplitudes in the respective hopping movement.

TABLE 1.

Kinetic and thermodynamic parameters for the reaction of the phospholipid derivatives with dithionite in all lipid bilayers tested

Probe Lipid bilayer composition ΔHo‡ (kJ mol−1) kR (M−1 s−1) at 35°C
NBD-DMPE POPC 85 ± 2 23 ± 3
NBD-lysoMPE 80 ± 4 48 ± 6
NBD-DMPE POPC/Chol (1:1) 79 ± 1 25 ± 2
NBD-lysoMPE 88 ± 1 36 ± 1
NBD-DMPE SpM/Chol (6:4) 66 ± 1 25 ± 1
NBD-lysoMPE 81 ± 1 51 ± 1
NBD-ethanolamine – 69 4.9×103
Open in a new tab

The parameters for the reaction with NBD-ethanolamine in aqueous media are also shown.

The experiment was performed as a function of temperature, and the enthalpies of activation recovered are also presented in Table 1. Significant differences may be observed when NBD-DMPE and NBD-LysoMPE are compared. Reaction of dithionite with NBD-LysoMPE shows a higher enthalpy of activation than reaction with NBD-DMPE for LUV in the liquid-ordered state and the opposite behavior is observed in bilayers that are in the liquid-disordered state. The dependence on the lipid composition of the bilayers is also significant with SpM/Chol (6:4) bilayers showing lower enthalpies of activation than POPC containing bilayers. The enthalpies of activation found for the reduction of NBD-ethanolamine in HEPES buffer is smaller than for the reduction of NBD phospholipids inserted in the lipid bilayers with the exception of NBD-DMPE in SpM/Chol (6:4) which has about the same value.

Translocation of NBD-DMPE and NBD-lysoMPE

The asymmetrically labeled LUV, with the required lipid composition and NBD phospholipid, were incubated at a given temperature and aliquots were taken at different incubation times (translocation time, 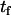Inline graphic). The amount of NBD in the outer monolayer was then calculated by the reaction with dithionite followed in a stopped flow apparatus at 25°C. Typical results obtained for the translocation of NBD-DMPE in LUV prepared from POPC at 35°C are presented in Fig. 1. The fluorescence signal was converted into concentration through the subtraction of the background signal and use of an independently determined conversion factor for the measured fluorescence intensity. In Fig. 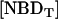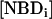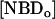1, the best fit of a single exponential to the time-dependent decrease in the concentration of NBD due to reaction with dithionite gives the total concentration of NBD, Inline graphic, and the concentration of NBD in the inner and outer monolayer, Inline graphic and Inline graphic respectively, and the rate of reaction with dithionite, 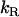Inline graphic. The translocation may be described by the set of differential equations (Eq. 1), where 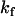Inline graphic is the rate of translocation:

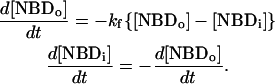graphic file with name M7.gif (1)

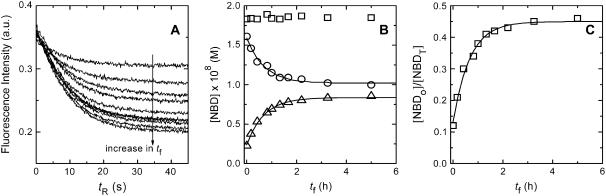
FIGURE 1.

FIGURE 1

Open in a new tab

Translocation of NBD-DMPE in POPC bilayers at 35°C. At given times of incubation (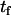Inline graphic) at 35°C, the amount of NBD-DMPE in the outer monolayer was measured by its reaction with dithionite (A). The experimental curve was fitted with a mono-exponential and the recovered total concentration of NBD-DMPE (□), the concentration in the outer (▵) and in the inner (○) monolayer are presented in B. The best fit of a mono-exponential to the time-dependence of the concentration of NBD-DMPE in the outer and inner monolayers is also shown (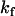Inline graphic = 2.0 × 10−4 s−1). The data can also be analyzed as the fraction of NBD-DMPE in the outer monolayer (C).

If there is no change in the total concentration of NBD and if the amount of NBD in the aqueous phase is negligible, Eq. 1 may be easily integrated and has the form of a mono-exponential. The translocation rate constant was obtained from the time dependence of either 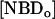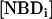Inline graphic, Inline graphic or from the fractional values of either of these relative to the total NBD concentration, [NBDT], in the asymmetrically labeled LUV, 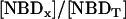Inline graphic, panels B and C in Fig. 1, respectively. For experiments done with NBD-DMPE, and within the same day, all methods resulted in the same value of 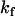Inline graphic. Small differences were, however, observed for translocation experiments that were measured during several days due to small changes in the response of the equipment. We have opted to routinely analyze the time-dependence of the fraction of NBD in the outer monolayer that is described by Eq. 2:

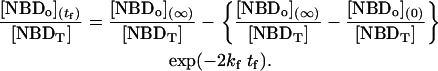graphic file with name M12.gif (2)

The derivation of Eq. 2 assumes negligible fraction of NBD in the aqueous phase and conservation of the total concentration of NBD. These conditions are valid for the case of NBD-DMPE that partitions predominantly into the lipid phase at all lipid compositions used and is chemically stable (1). For the lipid composition routinely used, 4 × 10−4 M, <1% of NBD-DMPE is in the aqueous phase for all lipid compositions and temperatures tested. However, the partition coefficient of NBD-lysoMPE is such that, for 10−3 M lipid concentration and 35°C, ∼3%, 9%, and 23% is present in the aqueous phase for LUV prepared from pure POPC, POPC/Chol (1:1), and SpM/Chol (6:4), respectively. Additionally, NBD-lysoMPE in the aqueous phase is chemically unstable with a significant degradation being detected after 8 h at 35°C (2). To overcome this problem, we have used higher concentrations of lipid, (3, 4, and 5) × 10−3 M for LUV prepared from pure POPC, POPC/Chol (1:1) and SpM/Chol (6:4), respectively. For those lipid concentrations, the fraction of NBD-lysoMPE in the aqueous phase is reduced to ≤5%, in all lipid compositions and temperatures tested. The degradation of this small fraction of NBD-lysoMPE in the aqueous phase does not significantly affect (<5%) the total concentration of NBD-lysoMPE during the time required to follow the translocation in LUV prepared from POPC or POPC/Chol at all temperatures tested. However, for LUV prepared from SpM/Chol, the translocation is much slower and the degradation was significant at low temperatures. For this system, only the results for temperatures ≥45°C are reported.

In the derivation of Eqs. 1 and 2, it was assumed that the rates of translocation from the inner to the outer monolayer (commonly called “flop”) and from the outer to the inner monolayer (commonly called “flip”) are the same. This assumption is justified by the finding that the fraction of amphiphile in each monolayer when equilibrium is attained is always 50 ± 5%. Additionally, for NBD-lysoMPE, the two rates were independently measured and the results could not be distinguished. They were both included in the average parameters shown in Fig. 2 and Table 2.

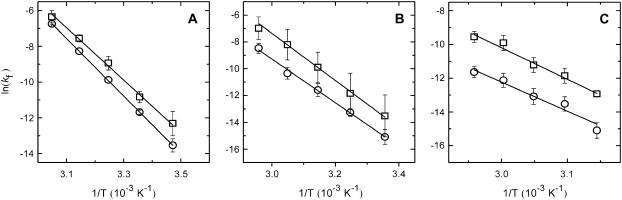
FIGURE 2.

FIGURE 2

Open in a new tab

Translocation rate for NBD-DMPE (□) and NBD-lysoMPE (○) in lipid bilayers prepared from pure POPC (A), POPC/Chol (1:1) (B), and SpM/Chol (6:4) (C). The error bars are the standard deviations of at least four independent experiments. The lines are the best fit of the absolute rate theory with the parameters presented in Table 2.

TABLE 2.

Kinetic and thermodynamic parameters for the translocation of the phospholipid derivatives in all lipid bilayers tested

Probe Lipid bilayer composition ΔHo‡ (kJ/mol) TΔSo‡ (kJ/mol)* ΔGo‡ (kJ/mol)*† kf* (s−1)
NBD-DMPE POPC 119 ± 5 21 ± 1 99 ± 1 (1.1 ± 0.4) × 10−4
NBD-lysoMPE 131 ± 2 30 ± 1 101 ± 1 (4.9 ± 0.8) × 10−5
NBD-DMPE POPC/Chol (1:1) 143 ± 14 38 ± 4 106 ± 4 (1 ± 1) × 10−5
NBD-lysoMPE 133 ± 5 23 ± 1 110 ± 1 (1.7 ± 0.5) × 10−6
NBD-DMPE SpM/Chol (6:4) 153 ± 11 39 ± 3 113 ± 1§ (4 ± 2) × 10−7§
NBD-lysoMPE 141 ± 12 23 ± 4 118 ± 1§ (7 ± 3) × 10−8§
Open in a new tab
*

At 35°C.

†

The standard deviations were calculated from the standard deviations of the rate constant at 35°C.

§

Those parameters are extrapolations from the best fit to the temperature range accessed experimentally (45–65°C). The standard deviations shown are the average of the standard deviations of the rate constants at the temperatures studied.

The first observation from Fig. 2 is that the translocation of NBD-DMPE is faster than the translocation of NBD-lysoMPE for all temperatures and lipid compositions tested. At 35°C, the translocation rate of the single chain phospholipid is about half of that for the double chain phospholipid in pure POPC bilayers. This difference is accentuated in bilayers in the liquid-ordered state where the rate constant for the single chain is ∼5 times smaller. The thermodynamic parameters of the translocation process may be obtained from the temperature-dependence of the rate constant using transition state theory (20) and are presented in Table 2. When the translocation of NBD-DMPE and NBD-lysoMPE are compared, one finds that the change in enthalpy, 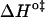Inline graphic, when going from the initial state (probe inserted in the bilayer) to the transition state is higher for NBD-lysoMPE in LUV in the liquid-disordered state (prepared from pure POPC) and lower for bilayers in the liquid-ordered state (POPC/Chol and SpM/Chol). 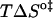The same behavior is found for the change in entropy, Inline graphic.

Another important, although expected, finding is the dependence of the translocation rate constant on the lipid composition of the bilayers. The translocation in bilayers in the liquid-disordered state (pure POPC) is faster than in bilayers prepared from POPC/Chol (1:1), this, in turn, being much faster then observed for bilayers prepared from SpM/Chol (6:4).

In Fig. 2, the large error associated with the results obtained for NBD-DMPE in POPC/Chol (1:1) bilayers is also evident. We have studied six independent samples but did not observe any decrease in the standard deviation toward values comparable to the ones observed for the other systems tested.

Permeability of bilayers to dithionite

We have also studied the permeability of the bilayers tested to dithionite by following the reduction of NBD. When dithionite is added to symmetrically labeled LUV, the temporal evolution of the system may be described by the following differential equations:

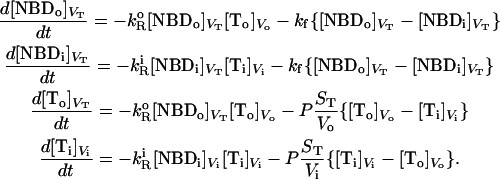graphic file with name M15.gif (3)

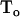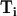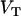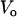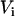Where Inline graphic and Inline graphic represent dithionite concentrations outside and inside LUV, respectively, and P is the permeability coefficient for dithionite. The subscripts Inline graphic, Inline graphic, and Inline graphic are the volumes to which the respective concentrations are referred, namely, the total volume of the reaction mixture, the volume outside, and the volume inside the LUV, respectively. The total surface area of the membrane, 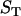Inline graphic, and the total aqueous volume inside the LUV, 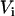Inline graphic, were calculated assuming that all LUV have a radius of 50 nm and using the literature values for the area per lipid (21). Thus, the number of lipid molecules in a LUV is 9.2 × 104 for POPC, 1.3 × 105 for POPC/Chol (1:1), and 1.5 × 105 for SpM/Chol (6:4). We have simplified Eqs. 3 by assuming that 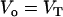Inline graphic (under the conditions used 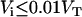Inline graphic) and also that the rate constant for the reaction with dithionite in the outer monolayer is equal to the rate constant in the inner monolayer (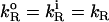Inline graphic). In Eqs. 3, we are also assuming that the permeability coefficient is equal for both directions and that the permeation of the membranes by dithionite does not alter the transmembrane electrical potential. The resulting set of differential equations was integrated numerically.

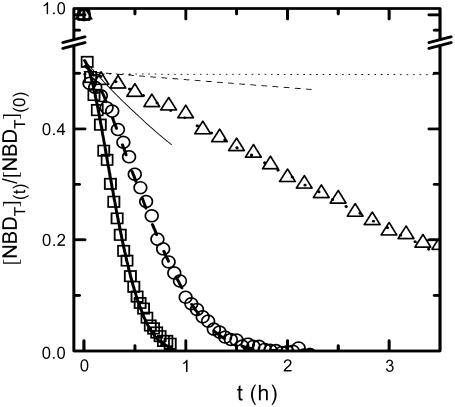
Typical results obtained for the complete curve of the decrease in NBD fluorescence due to reaction with dithionite are presented in Fig. 3 for the case of NBD-DMPE. The results obtained for NBD-lysoMPE, when analyzed with Eqs. 3, using the respective values of the rate constant for reaction with dithionite, led to the same values of the permeability constant. The data presented in Fig. 4 and Table 3 are averages of the results obtained for permeation of the membranes by dithionite using both NBD phospholipids as objects of the reduction process. In Figs. 3 and 4, it is evident that the permeability of bilayers composed of SpM/Chol (6:4) to dithionite is much smaller than the permeability of the other two lipid compositions, whereas POPC/Chol (1:1) bilayers are only slightly more impermeable to dithionite then POPC bilayers. This different behavior reflects the much higher enthalpy associated with the transition state in the process of permeation through SpM/Chol (6:4) bilayers, whereas for POPC/Chol(1:1) the enthalpy is only marginally higher than for POPC bilayers. The entropy change associated with the formation of the transition state goes in the same direction but is not enough to compensate for the higher enthalpy change in the more ordered bilayers.

FIGURE 3.

FIGURE 3

Open in a new tab

Typical results for the reduction of NBD-DMPE by dithionite added to the aqueous medium outside the liposomes at 35°C. For liposomes prepared from pure POPC (□, solid line), POPC/Chol (1:1) (○, dashed line), or SpM/Chol (6:4) (▵, dotted line). The thicker lines are the best fit of Eq. 3 to the experimental results and the thinner lines are the predicted results if the rate of reduction of NBD-DMPE initially in the inner monolayer is controlled by its translocation into the outer monolayer.

FIGURE 4.

FIGURE 4

Open in a new tab

Permeability coefficient of dithionite through lipid bilayers prepared from pure POPC (□), POPC/Chol (1:1) (○), or SpM/Chol (6:4) (▵). The error bars are the standard deviations of at least three independent experiments. The lines are the best fit of the absolute rate theory with the parameters presented in Table 3.

TABLE 3.

Kinetic and thermodynamic parameters for the permeability of dithionite, at 35°C, through the lipid bilayers tested

Lipid bilayer composition P (m s−1) × 1014 k (s−1) × 105 ΔGo‡ (kJ/mol)* ΔHo‡ (kJ/mol) TΔSo‡ (kJ/mol)
POPC 3.2 ± 0.9 8 ± 2 99.6 ± 0.7 95 ± 5 −4.5 ± 0.3
POPC/Chol (1:1) 1.7 ± 0.4 4.3 ± 0.9 101.3 ± 0.5 105 ± 3 3.9 ± 0.1
SpM/Chol (6:4) 0.17 ± 0.12 0.4 ± 0.3 107 ± 2 148 ± 10 41 ± 5
Open in a new tab
*

Standard deviations calculated from the standard deviations found experimentally for the permeability rate constant, k, at 35°C.

In Fig. 3, we also show the theoretically expected result if the reduction of NBD, initially present in the inner monolayer, is determined by its translocation into the outer monolayer as we had previously (1,2) assumed. The rate constants reported previously by us for the translocation of those NBD phospholipids were clearly overestimated.

DISCUSSION

The translocation rate constant for NBD-DMPE in POPC bilayers that we report here is almost identical to the published data for the translocation of other PE phospholipids modified with NBD in the polar headgroup (NBD-EggPE, NBD-DPPE and NBD-DOPE) in liquid-disordered bilayers (10). There is no data in the literature for NBD-lysoMPE or for the liquid-ordered phases. An important question that should be posed is whether the translocation rates obtained for a phospholipid modified with NBD in the polar headgroup are representative of the translocation rates of natural phospholipids. The rates obtained for NBD-DMPE in POPC are comparable to the ones found for the translocation of PC phospholipids (22,23) and for PC derivatized with TEMPO in the polar headgroup (24) for bilayers in the liquid-disordered state. In previous work by this laboratory, it was concluded that the kinetics and/or thermodynamics of interaction of NBD-DMPE (or NBD-lysoMPE) was comparable to that of DMPC (or LysoMPC) (1,2). Altogether, this is an indication that the polar NBD group covalently bound to the ethanolamine behaves similarly to a phosphocholine headgroup and gives support to the biological relevance of the data obtained in this work. A recent report (25), however, questions this conclusion.

We shall first discuss the differences in translocation rates for NBD-DMPE and NBD-LysoMPE in bilayers of the same chemical composition and at the same temperature (i.e., the same physical state). Translocation of the single-chain analog (NBD-LysoMPE) is always significantly slower than translocation of the two-chain species (NBD-DMPE). The interpretation of this unexpected result may be attempted on the basis of a decomposition of the Gibbs' free energy change, for the translocation transition state, into its enthalpic and entropic components (Table 2). The transition state for translocation of polar solutes may be assumed to be a state in which the solute lies in the central, apolar, region of the bilayer. This region has a low density and a high degree of disorder, and it is reasonable to assume that the transition state for both probe molecules used in this work has similar energies. When inserted in the bilayers, the single-chain derivative may be expected to create a local defect with larger entropy than the double-chain derivative. In this defect, the single-chain probe will also have less van der Waals' contact with the neighboring lipids in the bilayer than its double-chain homolog and, therefore, a larger enthalpy. 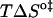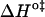In this view, the change to the transition state should present a smaller Inline graphic and Inline graphic than the double chain analog. This is what we observe for the bilayers in the liquid-ordered state (POPC/Chol, and SpM/Chol) but the opposite behavior is found for the bilayer in the liquid-disordered state (pure POPC).

The different translocation rates and thermodynamic parameters found for both phospholipid derivatives show that translocation is not only determined by the work done in placing the polar region of the amphiphile in the nonpolar bilayer center, contrary to the commonly accepted view. The structural and dynamic characteristics of the amphiphile microenvironment are also important. The slower translocation rate of the single-chain amphiphile is also of relevance in the field of pharmacokinetics. Although this amphiphile equilibrates much faster with the outer monolayer of cell plasma membrane, its internalization by passive diffusion may be less efficient than for a double-chain amphiphile. The amount of amphiphile in the inside of a cell (inner plasma membrane monolayer plus internal aqueous environment) is only determined by the slower step, which is the translocation for both amphiphiles.

Another important finding, although expected, is the decrease in the translocation rate for bilayers in the liquid-ordered state as compared to bilayers in the liquid-disordered state. Thus, compared to the translocation rate in liquid-disordered POPC bilayers, the translocation rate is between 11-fold (NBD-DMPE) and 29-fold (NBD-LysoMPE) slower in liquid-ordered POPC/Chol bilayers. This result is comparable to the literature data for the effect of cholesterol on the passive translocation of phospholipids (26). It may be interpreted as a consequence of the physical state of the bilayer (liquid-ordered or liquid-disordered state). There is no data in the literature for bilayers prepared from sphingomyelin and cholesterol but, with the above reasoning, one could expect a reduction of the translocation rate due to increased order in the bilayer. In fact, we observe a reduction between 275-fold (NBD-DMPE) and 700-fold (NBD-LysoMPE) in liquid-ordered SpM/Chol (6:4) bilayers compared with liquid-disordered POPC bilayers. When the two liquid-ordered state bilayers, POPC/Chol (1:1) and SpM/Chol (1:1), are compared, translocation is seen to be ∼25-fold slower in the latter than it is in the former. Thus, although POPC/Chol (1:1) membranes and SpM/Chol (6:4) membranes are both considered to be liquid-ordered bilayer phases, their properties are clearly very distinct with regard to translocation. Our previous studies (1,2) of the insertion and desorption rates in the association of these phospholipid derivatives with the same lipid bilayers had arrived at a similar conclusion. In face of those results, one might well ask the question whether all cholesterol-rich binary mixtures with phospholipids are necessarily liquid-ordered phases, whether all liquid-ordered phases are necessarily comparable, and indeed whether our definition of a liquid-ordered phase in terms of only the translational and conformational orders of the bilayers is adequate.

The permeability coefficient found for dithionite in POPC bilayers is 1–2 orders of magnitude smaller than the reported values for the permeability of the chloride ion (27–29). The results were well described by the model proposed supporting the assumption that the unidirectional flow of dithionite does not alter the transmembrane electric potential. The enthalpy change associated with the transition state on the permeation of dithionite through POPC bilayers is somewhat larger than found for the chloride anion, 80 kJ mol−1 (29) and smaller than the one found for NBD phospholipids. The value obtained in this study is close to the work predicted for moving a monovalent ion with its hydration shell, and a global radius of 4 Å, from water into a hydrocarbon liquid (30). For bilayers prepared from POPC/Chol (1:1), the enthalpy change associated with the permeability of dithionite is significantly higher than for POPC bilayers, being also smaller than the one found for the translocation of the NBD phospholipids. The enthalpies of both processes are comparable when the lipid bilayer composition is SpM/Chol (6:4).

It would be of interest to compare the rate constants for the translocation of the phospholipids and the permeation of dithionite. For this comparison, one should first convert the permeability coefficient into the first order rate constant of permeation. According to the usual microscopic model of permeation, and assuming only one energetic barrier in the permeation process and fast equilibrium between solute in bulk and at the membrane surface, the permeability coefficient is related with the permeation rate constant (k) by the expression (31–33)

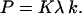graphic file with name M28.gif (4)

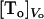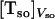K is the equilibrium constant that converts the bulk concentration of permeating solute into its concentration at the surface of the membrane. For dithionite in the outer aqueous solution, the above concentrations would be Inline graphicand Inline graphic, respectively. λ is a length parameter and is introduced to convert the concentration of solute from moles per unit volume into moles per unit surface (32). The major difficulty in using Eq. 4 is the lack of knowledge of the equilibrium constant. The data presented in Table 3 was calculated assuming that the concentration of dithionite in the bilayer surface relative to the volume of the surface is equal to the bulk concentration, which is equivalent to say that there are no attractive or repulsive interaction between dithionite and the lipid bilayer surface. Under this assumption, K = 1 and the length parameter, λ, should be the radius of the solute molecule (4 Å). The rate constants of permeation calculated from Eq. 4 are presented in Table 3 as are the thermodynamic parameters associated with this process (from the bilayer surface toward the transition state). The enthalpy change is the same as that found for the permeability coefficient because the equilibration between bulk aqueous media and the bilayer surface is achieved by random diffusion, an equilibrium with no enthalpy change associated, and we have assumed that there is no interaction between the dithionite and the bilayer surface. The rate constant may now be compared with those found for the translocation of the phospholipids as they reflect comparable processes and one finds that they are similar for bilayers in the liquid-disordered state (prepared from pure POPC) but significantly higher for bilayers in the liquid ordered state (prepared from mixtures of POPC and cholesterol or sphingomyelin and cholesterol).

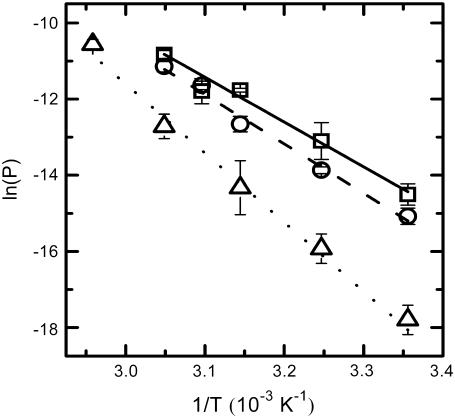
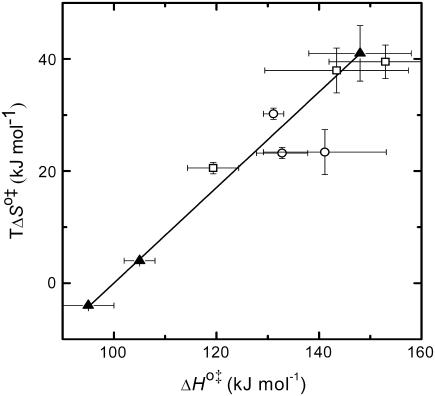
A strong positive correlation between the activation enthalpy and the activation entropy in the permeation of dithionite is observed in the different bilayers tested (Table 3). A linear relation between the enthalpy and entropy change was found previously for the transition state in the permeability of water in different lipid bilayers (34), for the solubility of different solutes in a homologous series between water and lipid bilayers (35), and also in a broad range of processes (36). This relation was first noted by Barclay-Butler and is more generally called enthalpy/entropy compensation (36). Due to the correlation in the errors of the estimates of the enthalpic and entropic components of the Gibbs' free energy, the plot of 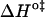Inline graphic versus 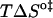Inline graphic is not recommended for inspection of enthalpy/entropy compensation (36,37). 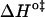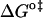Instead, the correlation between Inline graphic and Inline graphic should be inspected (38) and it is represented in Fig. 5 for the permeation and translocation processes studied in this work. A good linear relationship is evident for the case of dithionite permeability and a poor correlation is found for the case of the NBD-phospholipid translocation. 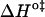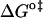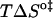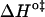The linear relation found between Inline graphic and Inline graphic (and consequently between Inline graphicand Inline graphic) in the permeability of dithionite shows that the energetics of the transition state in all bilayers tested follows a single source of additivity (36,39), despite the very different structure and dynamics of the bilayers (liquid-disordered and liquid-ordered from cholesterol and an unsaturated or saturated phospholipid).

FIGURE 5.

FIGURE 5

Open in a new tab

Representation of the enthalpic component versus the Gibbs' free energy of the activation state in the translocation of NBD-DMPE (□), translocation of NBD-LysoMPE (○), and permeability of dithionite (▴) in the lipid bilayers tested (data from Tables 2 and 3). The error bars are the standard deviations. The best fit of a straight line for the data on the permeability of dithionite is also shown.

This detailed study of dithionite permeability has several implications for the use of dithionite to assess the asymmetry of a given amphiphile or to measure its translocation/permeation across bilayers:

  1. For the lipid mixtures examined in this work, it is no longer necessary to experimentally determine whether dithionite permeability is significant or not during the asymmetry measurement, it may be calculated.

  2. The measurement of translocation/permeation by continuous reduction by dithionite is now possible for systems where the dithionite permeability is slower or comparable to the translocation/permeation because the two processes may be deconvoluted.

  3. Dithionite is an efficient reducing agent that may be used to bleach fluorophores other then NBD, although with a different rate constant, the knowledge of its permeability is therefore of unlimited value.

Understanding the physico-chemical details of translocation of amphiphilic molecules across lipid bilayers is of fundamental relevance in studies that deal with the maintenance of cell membrane lipid compositional asymmetry, lipid homeostasis, and drug transport across cell membranes. Particularly in the last case, the modeling of nonmediated amphiphilic drug transport (many psycho-mimetic drugs are amphiphiles) across “tight epithelia” such as the vascular endothelium that constitutes the blood-brain and placental barriers is an important aspect of pharmaco-kinetics and requires a quantitative knowledge of the rate constants involved. In principle, some general rules may be established in this regard based on studies in model membrane systems. These studies will have to be developed in consideration of various properties of the amphiphiles, including hydrophile/lipophile balances, shape factors, magnitude, and orientation of the amphiphile dipole moment relative to the electrical (surface electrostatic, transmembrane, and dipolar) potentials at the membrane surface, and formal charge of the amphiphile. The differences we report in this work between the translocation of NBD-DMPE and NBD-lysoMPE, discussed above, can be understood in terms of shape factors. A long, albeit rather well-defined, path of model membrane studies will have to be traversed before the general rules alluded to above can be clearly established. A further important aspect of this work and our earlier studies on amphiphile association with lipid bilayers (1,2,18,40,41) is that the kinetic rate constants of the association steps (insertion, translocation, and desorption) provide the largest known differences between liquid-ordered and liquid-disordered membrane phases (up to 2.5 orders of magnitude in the case of translocation (see Table 2). Since these phases are believed to be important in cell membrane physiology in what concerns lipid “rafts” (42), it is possible that the kinetics of amphiphile association with membranes may serve as an important tool in elucidating the existence and mass fraction of “rafts” in cell membranes.

Acknowledgments

This work was supported through research grants from the POCTI program of the Fundacao para a Ciência e a Tecnologia (FCT) of the Portuguese Ministry for Higher Education and Scientific Research. L.M.B.B.E.was supported by a doctoral stipend No. SFRH/BD/6746/2001 by the FCT.

References

  • 1.Abreu, M. S. C., M. J. Moreno, and W. L. C. Vaz. 2004. Kinetics and thermodynamics of association of a phospholipid derivative with lipid bilayers in liquid-disordered and liquid-ordered phases. Biophys. J. 87:353–365. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 2.Sampaio, J. L., M. J. Moreno, and W. L. C. Vaz. 2005. Kinetics and thermodynamics of association of a fluorescent lysophospholipid derivative with lipid bilayers in liquid-ordered and liquid-disordered phases. Biophys. J. 88:4064–4071. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 3.Mcintyre, J. C., and R. G. Sleight. 1991. Fluorescence assay for phospholipid membrane asymmetry. Biochemistry. 30:11819–11827. [DOI] [PubMed] [Google Scholar]
  • 4.McNamee, M. G., and H. M. McConnel. 1973. Transmembrane potentials and phospholipid flip-flop in excitable membrane vesicles. Biochemistry. 12:2951–2958. [DOI] [PubMed] [Google Scholar]
  • 5.Langner, M., and S. W. Hui. 1993. Dithionite penetration through phospholipid-bilayers as a measure of defects in lipid molecular packing. Chem. Phys. Lipids. 65:23–30. [DOI] [PubMed] [Google Scholar]
  • 6.Moss, R. A., and S. Bhattacharya. 1995. Transverse membrane asymmetry in model phospholipid-bilayers—NBD-phosphatidylethanolamine and the separation of flip from flop. J. Am. Chem. Soc. 117:8688–8689. [Google Scholar]
  • 7.Angeletti, C., and J. W. Nichols. 1998. Dithionite quenching rate measurement of the inside-outside membrane bilayer distribution of 7-nitrobenz-2-oxa-1,3-diazol-4-yl-labeled phospholipids. Biochemistry. 37:15114–15119. [DOI] [PubMed] [Google Scholar]
  • 8.Wang, T. Y., and J. R. Silvius. 2000. Different sphingolipids show differential partitioning into sphingolipid/cholesterol-rich domains in lipid bilayers. Biophys. J. 79:1478–1489. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9.Kol, M. A., A. I. P. M. de Kroon, D. T. S. Rijkers, J. A. Killian, and B. de Kruijff. 2001. Membrane-spanning peptides induce phospholipid flop: A model for phospholipid translocation across the inner membrane of E. coli. Biochemistry. 40:10500–10506. [DOI] [PubMed] [Google Scholar]
  • 10.Armstrong, V. T., M. R. Brzustowicz, S. R. Wassall, L. J. Jenski, and W. Stillwell. 2003. Rapid flip-flop in polyunsaturated (docosahexaenoate) phospholipid membranes. Arch. Biochem. Biophys. 414:74–82. [DOI] [PubMed] [Google Scholar]
  • 11.Huijbregts, R. P. H., A. I. P. M. deKroon, and B. deKruijff. 1996. Rapid transmembrane movement of C-6-NBD-labeled phospholipids across the inner membrane of Escherichia coli. Biochim. Biophys. Acta. 1280:41–50. [DOI] [PubMed] [Google Scholar]
  • 12.Langner, M., and S. W. Hui. 2000. Effect of free fatty acids on the permeability of 1,2-dimyristoyl-sn-glycero-3-phosphocholine bilayer at the main phase transition. Biochim. Biophys. Acta. 1463:439–447. [DOI] [PubMed] [Google Scholar]
  • 13.Koynova, R., and M. Caffrey. 1998. Phases and phase transitions of the phosphatidylcholines. Biochim. Biophys. Acta-Rev. Biomembranes. 1376:91–145. [DOI] [PubMed] [Google Scholar]
  • 14.Mateo, C. R., A. U. Acuna, and J. C. Brochon. 1995. Liquid-crystalline phases of cholesterol lipid bilayers as revealed by the fluorescence of trans-parinaric acid. Biophys. J. 68:978–987. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Sankaram, M. B., and T. E. Thompson. 1990. Interaction of cholesterol with various glycerophospholipids and sphingomyelin. Biochemistry. 29:10670–10675. [DOI] [PubMed] [Google Scholar]
  • 16.Bartlett, G. R. 1959. Phosphorus assay in column chromatography. J. Biol. Chem. 234:466–468. [PubMed] [Google Scholar]
  • 17.Taylor, R. P., A. V. Broccoli, and C. M. Grisham. 1978. Enzymatic and colorimetric determination of total serum-cholesterol–undergraduate biochemistry laboratory experiment. J. Chem. Educ. 55:63–64. [DOI] [PubMed] [Google Scholar]
  • 18.Abreu, M. S. C., L. M. B. B. Estronca, M. J. Moreno, and W. L. C. Vaz. 2003. Binding of a fluorescent lipid amphiphile to albumin and its transfer to lipid bilayer membranes. Biophys. J. 84:386–399. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 19.Hope, M. J., M. B. Bally, G. Webb, and P. R. Cullis. 1985. Production of large unilamellar vesicles by a rapid extrusion procedure—characterization of size distribution, trapped volume and ability to maintain a membrane-potential. Biochim. Biophys. Acta. 812:55–65. [DOI] [PubMed] [Google Scholar]
  • 20.Steinfeld, J. I., J. S. Francisco, and W. L. Hase. 1999. Chemical Kinetics and Dynamics. Prentice-Hall, Upper Saddle River, NJ.
  • 21.Smaby, J. M., M. M. Momsen, H. L. Brockman, and R. E. Brown. 1997. Phosphatidylcholine acyl unsaturation modulates the decrease in interfacial elasticity induced by cholesterol. Biophys. J. 73:1492–1505. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.Wimley, W. C., and T. E. Thompson. 1991. Transbilayer and interbilayer phospholipid exchange in dimyristoylphosphatidylcholine dimyristoylphosphatidylethanolamine large unilamellar vesicles. Biochem. 30:1702–1709. [DOI] [PubMed] [Google Scholar]
  • 23.deKruijff, B., and E. J. J. Vanzoelen. 1978. Effect of phase-transition on transbilayer movement of dimyristoyl phosphatidylcholine in unilamellar vesicles. Biochim. Biophys. Acta. 511:105–115. [DOI] [PubMed] [Google Scholar]
  • 24.Kornberg, R. D., and H. M. Mcconnel. 1971. Inside-outside transitions of phospholipids in vesicle membranes. Biochemistry. 10:1111. [DOI] [PubMed] [Google Scholar]
  • 25.Liu, J., and J. C. Conboy. 2005. 1,2-diacyl-phosphatidylcholine flip-flop measured directly by sum-frequency vibrational spectroscopy. Biophys. J. 89:2522–2532. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 26.Redelmeier, T. E., M. J. Hope, and P. R. Cullis. 1990. On the mechanism of transbilayer transport of phosphatidylglycerol in response to transmembrane pH gradients. Biochemistry. 29:3046–3053. [DOI] [PubMed] [Google Scholar]
  • 27.Hauser, H., D. Oldani, and M. C. Phillips. 1973. Mechanism of ion escape from phosphatidylcholine and phosphatidylserine single bilayer vesicles. Biochemistry. 12:4507–4517. [DOI] [PubMed] [Google Scholar]
  • 28.Nicholls, P., and N. Miller. 1974. Chloride diffusion from liposomes. Biochim. Biophys. Acta. 356:184–198. [DOI] [PubMed] [Google Scholar]
  • 29.Toyoshima, Y., and T. E. Thompson. 1975. Chloride flux in bilayer membranes—chloride permeability in aqueous dispersions of single-walled, bilayer vesicles. Biochemistry. 14:1525–1531. [DOI] [PubMed] [Google Scholar]
  • 30.MacDonald, R. C. 1976. Energetics of permeation of thin lipid-membranes by ions. Biochim. Biophys. Acta. 448:193–198. [DOI] [PubMed] [Google Scholar]
  • 31.Laidler, K. J., and K. E. Shuler. 1949. The Kinetics of membrane processes 1. The mechanism and the kinetic laws for diffusion through membranes. J. Chem. Phys. 17:851–855. [Google Scholar]
  • 32.Zwolinski, B. J., H. Eyring, and C. E. Reese. 1949. Diffusion and Membrane Permeability.1. J. Phys. Colloid. Chem. 53:1426–1453. [Google Scholar]
  • 33.Flewelling, R. F., and W. L. Hubbell. 1986. Hydrophobic ion interactions with membranes—thermodynamic analysis of tetraphenylphosphonium binding to vesicles. Biophys. J. 49:531–540. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 34.Sogami, M., S. Era, M. Murakami, Y. Seo, H. Watari, and N. Uyesaka. 2001. Application of the transition state theory to water transport across cell membranes. Biochim. Biophys. Acta. 1511:42–48. [DOI] [PubMed] [Google Scholar]
  • 35.Disalvo, E. A. 1988. Permeability of water and polar solutes in lipid bilayers. Adv. Colloid Interface Sci. 29:141–170. [DOI] [PubMed] [Google Scholar]
  • 36.Sharp, K. 2001. Entropy-enthalpy compensation: Fact or artifact? Protein Sci. 10:661–667. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 37.Krug, R. R., W. G. Hunter, and R. A. Grieger. 1976. Enthalpy-entropy compensation 1. Some fundamental statistical problems associated with analysis of van't Hoff and Arrhenius data. j. phys. Chem. 80:2335–2341. [Google Scholar]
  • 38.Krug, R. R., W. G. Hunter, and R. A. Grieger. 1976. Enthalpy-entropy compensation 2. Separation of chemical from statistical effect. J. Phys. Chem. 80:2341–2351. [Google Scholar]
  • 39.Lumry, R. 1995. On the interpretation of data from isothermal processes. Methods Enzymol. 259:628–720. [DOI] [PubMed] [Google Scholar]
  • 40.Estronca, L. M. B. B., M. J. Moreno, J. A. N. Laranjinha, L. M. Almeida, and W. L. C. Vaz. 2005. Kinetics and thermodynamics of lipid amphiphile exchange between lipoproteins and albumin in serum. Biophys. J. 88:557–565. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 41.Estronca, L. M. B. B., M. J. Moreno, M. S. C. Abreu, E. Melo, and W. L. C. Vaz. 2002. Solubility of amphiphiles in membranes: influence of phase properties and amphiphile head group. Biochem. Biophys. Res. Commun. 296:596–603. [DOI] [PubMed] [Google Scholar]
  • 42.Simons, K., and W. L. C. Vaz. 2004. Model systems, lipid rafts, and cell membranes. Annu. Rev. Biophys. Biomol. Struct. 33:269–295. [DOI] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES